关于不定方程x3±64=73y2*

郑 爱 琳

(西南大学 数学与统计学院, 重庆 400715)



关于不定方程x3±64=73y2*

郑 爱 琳

(西南大学 数学与统计学院, 重庆 400715)

摘要：不定方程是数论研究的一个重要分支，不仅其自身发展活跃，而且离散数学的各个领域也有重要的应用，对于解决现实问题有着重要的作用.主要利用pell方程、递归数列、同余式和平方剩余几种初等方法，针对D=73时，不定方程x3±64=Dy2的解进行讨论，证明了不定方程x3±64=73y2仅有整数解(x,y)=(∓4,0).

关键词：不定方程;整数解;递归数列;同余式

方程

x3±64=Dy2,x,y∈Z

(1)

(其中D为大于零的正整数)是一类基本而重要的不定方程，对它已有不少的研究工作.当D>2,D无平方因子且不能被3或6k+1的素数整除时，方程的解已经由文献[1]给出.但是当D为不含平方因子，并且能被3或6k+1的素数整除时，张攀[2]证明了当D=7,13,19,37,43时方程(1)的所有整数解.赵天[3]证明了不定方程x3+64=Dy2,当D=21时，仅有整数解(x,y)=(-4,0),(5,±3).牛芳芳[4]证明了不定方程x3-64=31y2仅有整数解(x,y)=(-4,0),(20,±16),(7,±3).董小倩[5]证明了不定方程x3±64=67y2仅有整数解(x,y)=(∓4,0).而对于D=73时不定方程的解还未解决.此处在此基础上，利用同余式的性质和递归数列的方法，证明了该方程只有平凡解(x,y)=(∓4,0).

引理 1[6]不定方程

x3-1=73y2,x,y∈Z

(2)

仅有整数解(x,y)=(1,0).

定理 1不定方程

x3-64=73y2,x,y∈Z

(3)

仅有整数解(4,0).

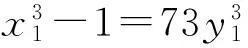
当x≡1(mod 2)时，式(3)化为(x-4)(x2+4x+16)=73y2，易知(x-4,x2+4x+16)=1或3，故式(3)有4种可能的分解：

情形1x-4=73a2，x2+4x+16=b2，y=ab.

情形2x-4=a2，x2+4x+16=73b2，y=ab.

情形3x-4=219a2，x2+4x+16=3b2，y=3ab.

情形4x-4=3a2，x2+4x+16=219b2，y=3ab.

以下分别讨论这4种情形所给式(3)的整数解.

情形1由x2+4x+16=b2可得x=0或-4,均不适合x-4=73a2，故该情形无式(3)的解.

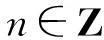
(4)

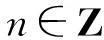
(5)

(6)

(7)

其中n∈Z，显然-6≤xn≤6，从而式(4)(5)只须取自

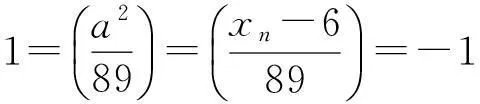
情形3和情形4由于x≡1(mod 2)，所以x2≡1(mod 4)，代入情形3和情形4的第二式可知均有3b2≡1(mod 4)，这不可能，故情形3和情形4都无解.

综合上述4种情形的讨论可知，不定方程x3-64=73y2仅有整数解(x,y)=(4,0).

引理 2不定方程

x3+1=73y2,x,y∈Z

(10)

仅有整数解(x,y)=(-1,0).

定理 2不定方程

x3+64=73y2,x,y∈Z

(11)

仅有整数解(x,y)=(-4,0).

当x≡1(mod 2)时，式(11)化为(x+4)(x2-4x+16)=73y2，易知(x+4,x2-4x+16)=1或3，故式(11)有4种可能的分解：

情形1x+4=73a2，x2-4x+16=b2，y=ab.

情形2x+4=a2，x2-4x+16=73b2，y=ab.

情形3x+3=219a2，x2-4x+16=3b2，y=3ab.

情形4x+4=3a2，x2-4x+16=219b2，y=3ab.

以下分别讨论这4种情形所给式(11)的整数解.

情形1由x2-4x+16=b2可得x=0或4均不适合x+4=73a2，故该情形无式(11)的整数解.

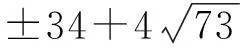
(12)

(13)

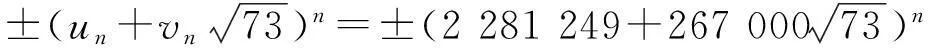
a2=xn+6

(14)

(15)

其中n∈Z，显然-6≤xn≤6，从而式(12)(13)只须取自

n∈Z

(16)

n∈Z

(17)

首先讨论式(14)，由式(16)易得递推关系：

(18)

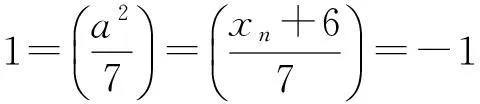
情形3和情形4由于x≡1(mod 2)，所以x2≡1(mod 4)，代入可知均有3b2≡1(mod 4)，这不可能，故情形3和情形4都无解.

综合上述4种情形的讨论可知，不定方程x3+64=73y2仅有整数解(x,y)=(-4,0).

参考文献(References)：

[1]张海燕，李复中.关于丢番图方程x3±64=Dy2[J].哈尔滨科学技术大学学报(自然科学版)，1994，18(2)：107-109

ZHANG H Y，LI F ZH.On Diophantine Equationx3±64=Dy2[J].Journal of Harbin science and Technology University:Natural Science Edition，1994，18(2)：107-109

[2] 张攀.关于不定方程x3±64=py2的研究[D].西安：西北大学,2012

ZHANG P.On Diophantine Equationx3±64=py2[D].Northwest University,2012

[3] 赵天.关于不定方程x3+64=21y2[J].重庆工商大学学报(自然科学版)，2008，25(1)：9-10

ZHAO T.On Diophantine Equationx3±64=Dy2[J]. Journal of Industrial and Commercial University Of Chongqing:Natural Science Edition, 2008,25(1):9-10

[4]牛芳芳.关于不定方程x3-64=31y2[J].重庆文理学院学报(自然科学版)，2012，31(2)：32-33

NIU F F.On Diophantine Equationx3±64=Dy2[J].Journal of Chongqing Academy of Arts and Sciences(Natural Science Edition),2012,31(2):32-33

[5] 董小倩.关于不定方程x3±64=73y2[J]. 重庆工商大学学报(自然科学版),2014，31(10)：13-15

DONG X Q.On Diophantine Equationx3±64=Dy2[J].Journal of Industrial and Commercial University Of Chongqing(Natural Science Edition),2014，31(10)：13-15

[6] 黎进香，赵明.关于不定方程x3-Dy2=1(D=61,73,91)[J].广西民族学院学报(自然科学版)，2005，11(1)：63-66

LI J X,ZHAO M.On Diophantine Equationx3±64=Dy2[J].Journal of Guangxi University for Nationalities(Natural Science Edition),2005,11 (1):63-66

责任编辑：李翠薇

On Diophantine Equationx3±64=73y2

ZHENG Ai-lin

(School of Mathematics and Statistics, Southwest University, Chongqing 400715, China)

Abstract：The Diophantine equation is an important branch of number theory research, not only itself development is active but also it has important application in discrete mathematics, as a result, it plays an important role in solving real problems. Many scholars at home and abroad extensively and deeply study it for many years. By the elementary methods such as pell equation, recurrent sequence, congruence expression, and square residue, the solution to the Diophantine equation x3±64=Dy2 is discussed when D=73, and this paper proves that the Diophantine equation x3±64=73y2 only has integer solution (x,y)=(∓4,0).

Key words：Diophantine equation; integer solution; recurrent sequence; congruence expression

中图分类号：O156

文献标志码：A

文章编号：1672-058X(2016)01-0026-04

作者简介：郑爱琳(1990-),女,甘肃会宁人, 硕士研究生, 从事计算数论研究.

*基金项目：国家自然科学基金(11471265).

收稿日期：2015-09-27；修回日期：2015-10-09.

doi:10.16055/j.issn.1672-058X.2016.0001.006