电磁力对双分裂导线舞动的影响

周林抒， 严　波,2， 赵　洋， 张　亮

(1.重庆大学 航空航天学院，重庆　400044； 2.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆　400044)



电磁力对双分裂导线舞动的影响

周林抒1， 严波1,2， 赵洋1， 张亮1

(1.重庆大学 航空航天学院，重庆400044； 2.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆400044)

摘要：基于一种计算导线间电磁力的数值方法，利用ABAQUS软件的用户自定义子程序UEL，编写计算子导线间电磁力的单元，实现考虑电磁力的双分裂导线舞动数值模拟方法。利用算例验证了方法和程序的正确性，进而对不同档距覆冰双分裂导线在不同电流强度下的舞动过程进行数值模拟，分析电磁力对线路舞动特征的影响。结果表明，档距较小时电磁力对线路舞动影响很小；档距较大时，电磁力对舞动的影响明显，甚至可能造成两子导线的碰撞。因而，在研究较大档距线路舞动时，有必要考虑电磁力的影响。

关键词：电磁力；双分裂导线；舞动；数值模拟

近年来，输电线路舞动事故在我国呈增长趋势，是威胁输电线路运行安全的重要因素之一。导线舞动具有持续时间长、幅值大等特点，可能造成线路跳闸、导线和金具的破坏，甚至导致断线倒塔等严重事故。舞动及其防治技术的研究具有重要意义。

数值模拟方法已成为研究覆冰导线舞动的重要手段。Desai等[1]较早建立了导线舞动的平衡方程，研究了模拟覆冰导线舞动的有限元方法。Zhang等[2]建立了覆冰分裂导线混合模型，将分裂导线等效为一根导线，并采用振型叠加法求解有限元方程，模拟研究了分裂导线的舞动。何锃等[3]采用振型叠加法对分裂导线的舞动进行了数值模拟。孙珍茂等[4]以考虑扭转的索单元模拟输电导线舞动，并分析了舞动振幅和风速的关系。李黎等[5]将分裂导线等效为单根导线，对连续多档导线舞动进行了数值仿真分析，研究了风速与初始攻角对舞动的影响。这些研究工作均没有考虑分裂导线各子导线之间空气动力特性的差异。严波等[6-10]对覆冰分裂导线舞动进行了研究，考虑了分裂导线各子导线气动特性的不同。然而，这些研究中均未考虑子导线间电磁力对导线舞动的影响。

实际线路运行过程中，可能会由于电磁力过高而产生分裂导线的粘连事故[11-13]。现场也观测到过子导线之间的“鞭击”现象，说明电磁力的作用不容忽视。Metha等[14]给出了一种计算导线电磁力的数值方法，该方法可通过ABAQUS用户自定义程序实现，与已有的舞动模拟方法相结合。基于这一方法，本文实现了考虑电磁力的舞动数值模拟方法，并研究了电磁力对覆冰双分裂线路的舞动的影响。研究结果对覆冰分裂导线舞动特征研究具有重要的参考价值。

1子导线间电磁力计算方法

1.1任意构形子导线间电磁力计算

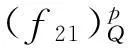
(1)

式中:μ0为真空磁导率，取4π×10-7H/m。

图1　两平行直导线间的电磁力Fig.1 Illustration of electromagnetic force for two straight and parallel conductors

分裂导线舞动过程中，由于迎风侧导线尾流对背风侧导线的作用，各子导线的气动特性不同，子导线运动过程中可能不再保持平行。文献[14]给出了一种计算分裂导线子导线间电磁力的数值方法。假设两条有限长任意弯曲的导线C1和C2，分别通有I1和I2大小的电流，每根导线划分N个单元，见图2。

图2　两任意弯曲导线电磁力作用Fig.2 Electromagnetic force for two arbitrarily curved conductors

导线C2上单元q受到导线C1上单元p的电磁力作用如下：

(2)

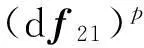
(3)

详细的计算方法和过程参见文献[14]。

1.2电磁力计算在ABAQUS中的实现

导线运动过程中，子导线间不同位置处的距离会发生变化，因而导线不同位置处的电磁力也会发生变化，即电磁力与导线的运动状态有关。在模拟输电线路舞动时，作者利用ABAQUS用户自定义单元程序UEL定义气动载荷单元，该单元无质量和刚度，通过与离散导线的索单元共节点的方式，实现随导线运动状态变化的气动载荷的施加[6]。为此，基于1.1节介绍的电磁力计算方法，在气动载荷单元中增加电磁力的计算，将气动载荷与电磁力叠加后施加在导线上。

利用文献[14]中的算例验证导线之间电磁力计算程序的正确性。算例参数如下：双分裂导线的档距为304.8 m，弧垂为12.192 m，子导线间相互平行时间距为0.457 m，每根子导线通有10 000 A电流。采用γ表示每根子导线受电磁力吸引后与垂直方向之间的角度，见图3。引入参数λ

(4)

计算不同角度下导线所受电磁力。式(4)中，γmax为两根子导线在档距中点处接触时的角度。

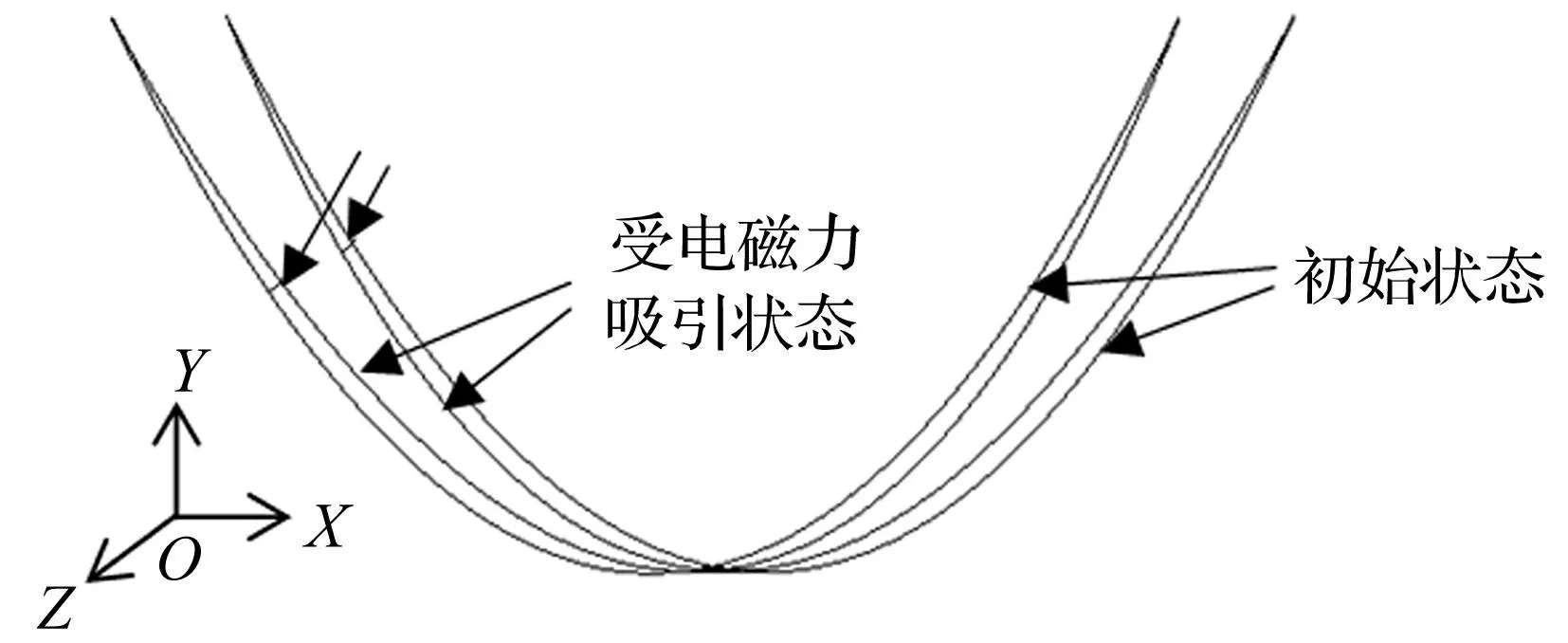
图3　双分裂导线受电磁力作用前后状态示意图Fig.3 Status of twin bundle conductor with and without electromagnetic force

利用编写的ABAQUS用户自定义单元程序，分别计算λ=0.0，0.2，0.4，0.6和1.0时每根子导线沿轴向分布的电磁力，结果如图4所示。所得计算结果与文献[14]给出的结果完全一致，验证了程序的正确性。从图中可见，当λ=0.0时，即两根子导线相互平行，电磁力除了在导线两端由于边界效应引起的变化外，其它位置的电磁力几乎相同。随着λ增大，由于导线两端点的间距不变，导线从两端向档中点的间距变小，电磁力逐渐变大，档中点的间距最小，电磁力最大。

图4　双分裂导线在不同张开角度下所受电磁力Fig.4 Electromagnetic force between two conductors in various yaw angles

2覆冰双分裂导线模型及其动力特性

模拟研究档距分别为100 m和200 m的典型覆冰双分裂孤立档线路的舞动，两线路导线在重力作用下的弧垂分别为1.78 m和2.53 m。导线型号为LGJ-500/45，直径为30.0 mm，两根子导线的间距为450 mm。导线的杨氏模量为3.25×104MPa，Poisson比为0.3，密度为2 519 kg/m3。100 m和200 m档距线路分别安装1个和2个相内间隔棒，采用等间距排布方式。假设导线覆冰为新月形，覆冰厚度12 mm。覆冰双分裂导线的阻力系数、升力系数和扭矩系数随风攻角的变化由风洞试验测得。值得一提的是，导线运动过程中两子导线的相对位置不断变化，其气动特性也会发生变化。由于覆冰导线气动特性随两子导线相对位置变化十分复杂，本文暂忽略这一影响。导线的阻尼采用Rayleigh阻尼模型，阻尼比取0.5%[15]。

覆冰导线采用具有扭转自由度的索单元模拟，在ABAQUS中可通过释放空间梁单元结点的弯曲自由度，保留扭转自由度，将材料设置为不可压缩来模拟这种索单元[6]，每根导线划分1 200个单元；间隔棒采用B31空间梁单元模拟，每个间隔棒划分1个单元。单元划分满足单元收敛性要求。由于线路为孤立档，模型两端设置为固定约束，并忽略耐张绝缘子串的影响，将其用等长的导线代替。建立的档距200 m线路的有限元模型如图5所示。

对于220 kV输电线路中常采用的LGJ-500/45型号的导线，该导线的最大运行电流为1 500 A[13]，每根子导线的电流为750 A。实际运行电流和负荷有关，一般不会满负载运行。为了分析电流强度对导线舞动的影响，考虑无电流，即I=0 A和I=500 A及I=750 A三种情况。为研究电磁力对导线舞动特征的影响，首先计算两线路在无电流下的动力特性，如表1所示。进一步计算了在电流强度为500 A和750 A时线路的动力特性，结果表明，相同档距导线在不同电流下的前三阶固有频率和模态几乎一致，即电磁力对导线的动力特性几乎没有影响。

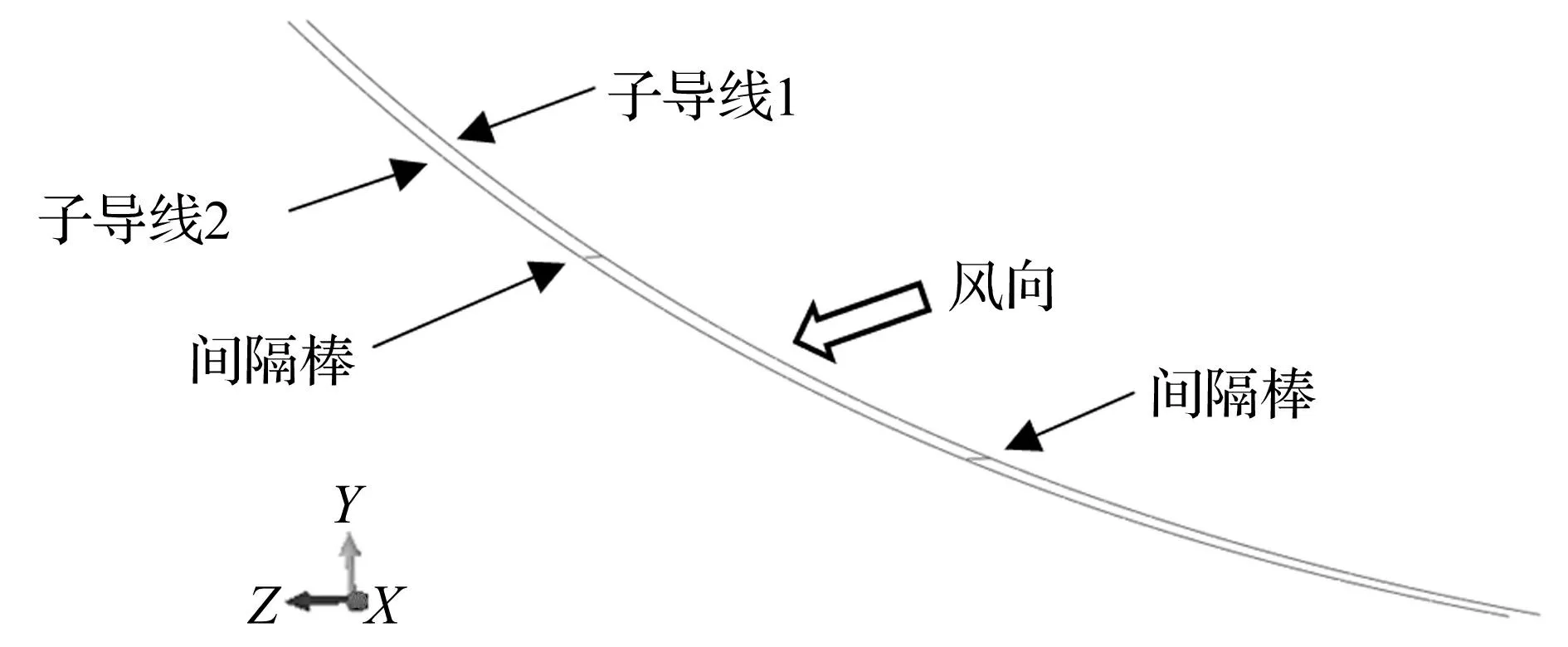
图5　双分裂导线有限元模型Fig.5 Finite element model of twin bundle conductor line

方向模态固有频率/Hz档距100m档距200m面内0.801.502.250.460.751.13面外0.751.512.250.370.751.13一个半波0.930.53扭转二个半波1.520.87三个半波2.311.14

3考虑电磁力时覆冰双分裂导线的舞动

3.1不同电流强度时导线的间距

利用ABAQUS有限元程序，并调用计算电磁力的用户自定义程序，计算得到不同电流强度下导线的平衡状态。图6为电流为750 A时导线的平衡状态，可见，在电磁力作用下，两导线相互吸引。

图7为该两线路两子导线最小间距随电流的变化。100 m档距线路安装了1根间隔棒，电磁力作用下两子导线在次档距中点，即1/4和3/4档距处的间距最小；200 m档距线路安装了2根间隔棒，在档距中点导线的间距最小。可见，在电流500 A时，100 m档距线路导线的最小间距为0.439 m，200 m档距线路导线的最小间距为0.430 m。在最大运行电流750 A时两线路导线的最小间距分别为0.425 m和0.405 m。

图6　电流为750 A时两线路的平衡状态(位移放大倍数：7)Fig.6 Equilibrium states of twin bundle conductor lines under current 750 A

图7　子导线最小间距随电流强度的变化Fig.7 Minimum conductor clearance varying with current

3.2电流强度对导线舞动的响应

基于已获得的分裂导线舞动数值模拟方法[6]，考虑电磁力时，在时间步迭代过程中计算气动载荷的同时，根据子导线当前运动状态计算电磁力，并将电磁力和气动载荷叠加即可。电磁力的计算方法和程序实现如第1节中所述。现利用本文得到的考虑电磁力的舞动数值模拟方法，模拟档距100 m和200 m线路的舞动过程，并分析不同电流强度对导线舞动的影响。

(1) 档距100 m线路

图8为风速为10 m/s，档距100 m线路子导线1在电流为500 A时次档距中点处的位移时程曲线。从图中可以看出，导线在500 A电流时舞动达到一个极限环。计算结果还表明，在无电流0 A和最大运行电流750 A时导线舞动均达到极限环，图9为不同电流下该点的舞动极限环。可见，在给定的电流范围内，导线的舞动轨迹差别很小，均为椭圆，即该线路的舞动模式受电流强度的影响很小。

图10为不同电流下该线路次档距中点处子导线间距的时程曲线。可见，导线舞动过程中，两子导线的间距在一个平衡位置附近振荡，平衡位置对应的间距随电流强度的增大而减小，而其振荡幅值随电流强度的增大而增大。

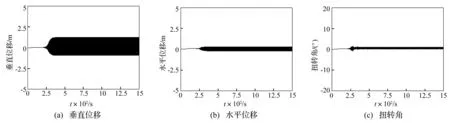
图8　电流500 A时档距100 m线路子导线1次档距中点位移时程Fig.8 Time histories of displacements at sub-span mid-point of sub-conductor 1 in 100 m-span line under current 500 A

图9　不同电流强度下档距100 m线路次档距中点的舞动轨迹Fig.9 Galloping orbits at sub-span mid-point of 100m-span line under various currents

(2) 档距200 m线路

图11为风速为10 m/s，档距200 m线路在不同电流下子导线1中点的位移时程，图12所示为相应点的舞动轨迹。从图中可以看出，在不考虑电流影响(电流为0 A)时，导线的运动达到一极限环，舞动轨迹为椭圆。在500 A电流时子导线的运动轨迹接近于椭圆状，但不能得到稳定的极限环。当电流达到750 A时，子导线的垂直位移振幅先增大后减小，水平位移振幅有明显的波动。可见，对于档距200 m线路，电流强度对导线的舞动有较明显的影响，且在最大运行电流750 A时，电磁力对导线舞动有一定的抑制作用。

图10　不同电流下档距100 m线路次档距中点子导线间距时程Fig.10 Time histories of conductor clearances at sub-span mid-point of 100 m-span line under various currents

图11　不同电流下档距200 m线路子导线1次档距中点位移时程Fig.11 Time histories of displacements at mid-point of sub-conductor 1 in 200 m-span line under various currents

图12　不同电流强度下档距200 m线路中点的舞动轨迹Fig.12 Galloping orbits at mid-point of 200 m-span line under various currents

由于该线路舞动时以单半波形态振动，其档中点处子导线的间距为整档中子导线的最小间距，图13所示为不同电流时该线路中点子导线间距的时程曲线。由图可见，在不考虑电流影响时，子导线间距的波动较小，且较平稳；当电流达到500 A和750 A时，子导线之间的间距波动更加剧烈，子导线的最小间距出现了零的情况，即两根子导线发生了碰撞，出现了所谓的“鞭击”现象。

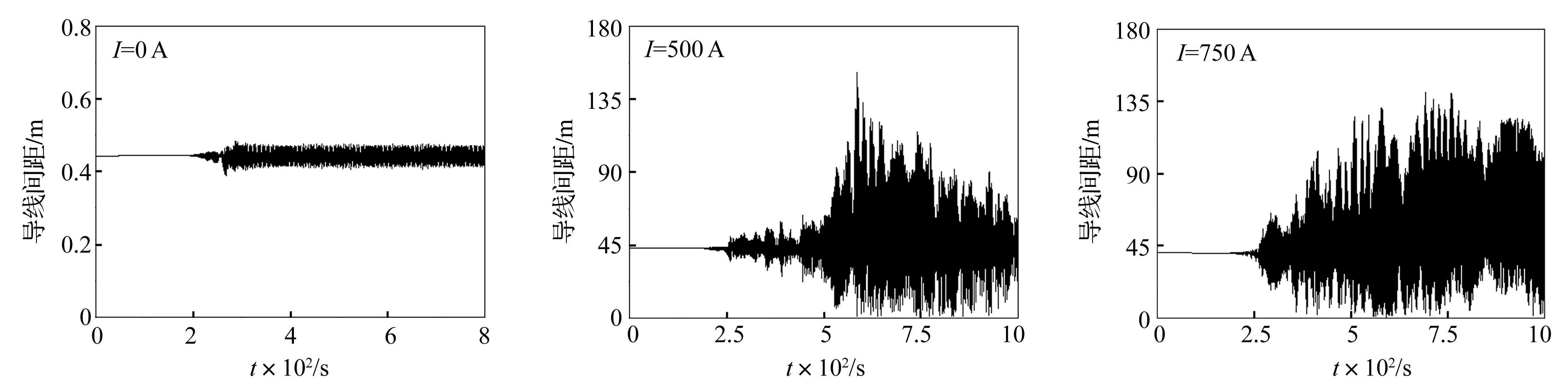
图13　不同电流下档距200m线路中点子导线间距时程Fig.13 Time histories of conductor clearances at mid-point of 200m-span line under various currents

3.3舞动响应频谱分析

本节利用导线位移的频谱分析电流强度对导线舞动特征的影响。由前述分析可知，电流强度对档距100 m线路舞动响应影响非常小，不同电流下的频率响应几乎相同。导线的舞动频率均接近面内单半波模态对应的固有频率。

图14为不同电流下，档距200 m线路子导线1中点的位移和扭转角响应频谱。可见，在不同电流下，导线面内、面外和扭转频率在0.45 Hz附近都会出现一个峰值，该频率接近面内单半波模态对应的频率0.46 Hz，因此，导线舞动以垂直单半波为主。值得注意的是，在电流500 A时位移响应的模态成分相对较多，但舞动主频并未发生变化，结合图12可知，在电流500 A时导线的舞动模式仍然以垂直单半波为主。

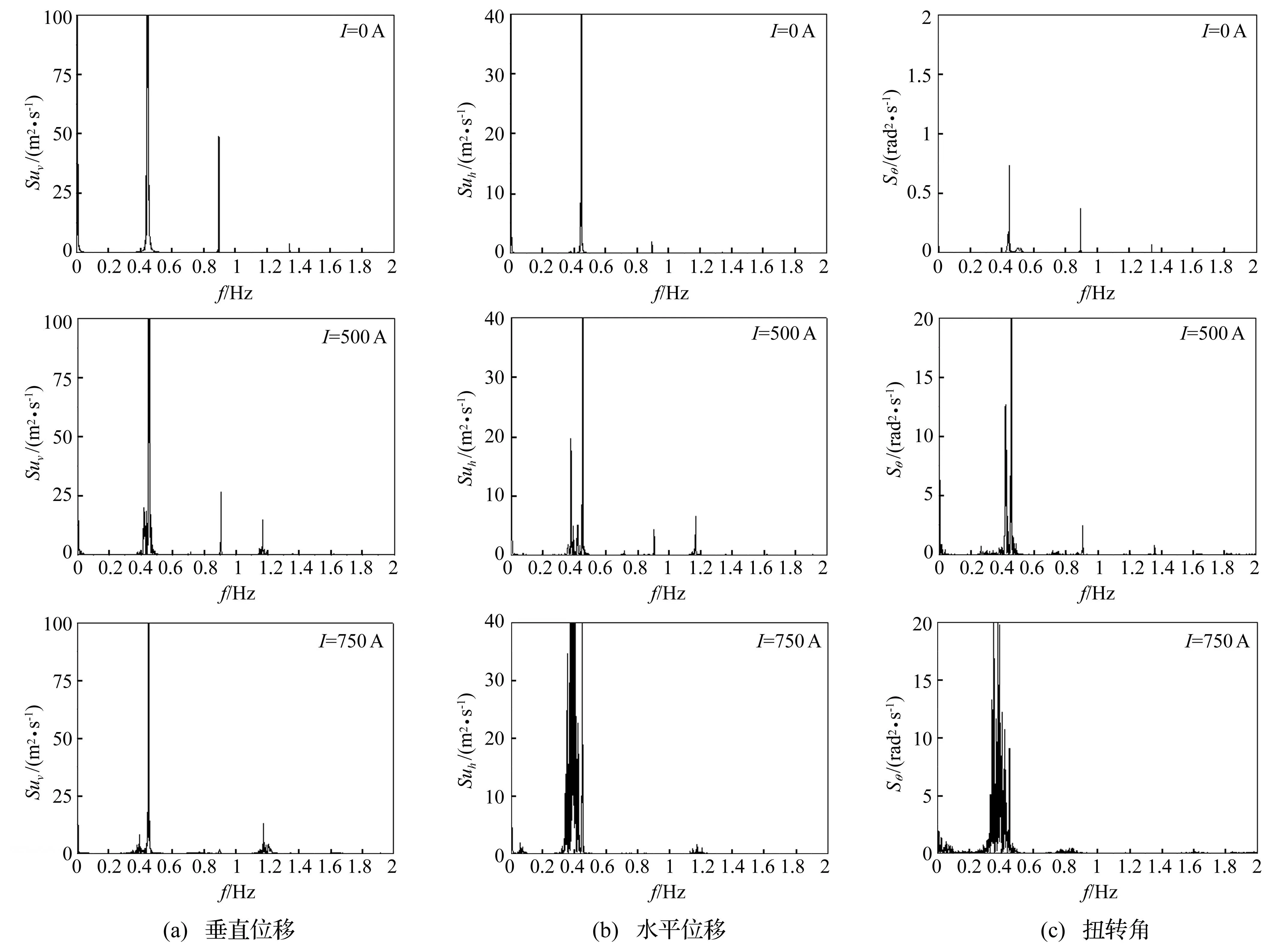
图14　不同电流下档距200 m线路子导线1中点位移及扭转角响应频谱Fig.14 Power spectra of displacements at sub-conductor 1 mid-point of 200 m-span line under various currents

4结论

本文通过ABAQUS软件的用户自定义单元模块，编写了模拟导线舞动时考虑子导线间电磁力的用户子程序，利用算例验证了程序的正确性。进而模拟研究了电流强度对覆冰双分裂导线舞动的影响。得到如下结论：

(1) 电流强度对100 m和200 m档距双分裂线路的动力特性几乎没有影响。

(2) 电磁力会对两子导线产生吸引力作用，两子导线在相内间隔棒之间的次档距中点间距最小，且最小间距随电流增大而减小。

(3 对于100 m小档距线路，舞动模式受电流强度影响很小。

(4) 对于档距200 m线路，电流强度对导线的舞动有较明显的影响，两根子导线可能发生碰撞；在最大运行电流750 A时，电磁力对导线舞动可能产生一定的抑制作用。

(5) 本文得到的数值模拟方法可以扩展用于模拟研究其它多分裂线路的舞动。

参 考 文 献

[ 1 ] Desai Y M, Yu P, Popplewell N, et al.Finite element modeling of transmission line galloping[J].Computers & Structures, 1995, 57(3):407-420.

[ 2 ] Zhang Q, Popplewell N, Shah A H.Galloping of bundle conductor[J].Sound and Vibration, 2000, 234(1):115-134.

[ 3 ] 何锃，赵高煜.分裂导线扭转舞动分析的动力学建模[J].工程力学, 2001, 18(2):126-134.

HE Zeng，ZHAO Gao-yu．On galloping of bundled conductors in an overhead transmission line with large torsional motion[J]．Engineering Mechanics，2001，18(2)：126-134.

[ 4 ] 孙珍茂，楼文娟.覆冰输电导线舞动非线性有限元分析[J].电网技术, 2010, 34(12):214-218.

SUN Zhen-mao，LOU Wen-juan．Nonlinear finite element analysis on galloping of ice-coated transmission line[J]．Power System Technology，2010，34(12)：214-218.

[ 5 ] 李黎，陈元坤，夏正春，等.覆冰导线舞动的非线性数值仿真研究[J].振动与冲击, 2011, 30(8):107-111.

LI Li，CHEN Yuan-kun，XIA Zheng-chun，et al． Nonlinear numerical simulation study of iced conductor galloping[J]．Journal of Vibration and Shock，2011，30(8)：107-111.

[ 6 ] Hu J, Yan B, Zhou S, et al.Numerical investigation on galloping of iced quad bundle conductors[J].IEEE Transactions on Power Delivery, 2012, 27(2):784-792.

[ 7 ] Yan Bo, Liu Xiao-hui, LÜ Xin, et al.Investigation into galloping characteristics of iced quad bundle conductors[J]. Journal of Vibration and Control,2014(6):538479.

[ 8 ] 严波，胡景，周松，等.覆冰四分裂导线舞动数值模拟及参数分析[J].振动工程学报, 2010, 23(3):310-316.

YAN Bo， HU Jing，ZHOU Song，et al．Numerical simulation and parameter analysis of galloping for iced quad-bundled conductor [J]. Journal of Vibration Engineering,2010,23(3):310-316.

[ 9 ] 周林抒，严波，杨晓辉，等.真型试验线路六分裂导线舞动模拟[J].振动与冲击, 2014, 33(9):6-11.

ZHOU Lin-shu, YAN Bo, YANG Xiao-hui, et al. Galloping simulation of six-bundle conductors in a transmission test line [J]. Journal of Vibration and Shock，2014，33(9)：6-11.

[10] 崔伟，严波，杨晓辉，等.双分裂导线间隔棒防舞数值模拟研究[J].振动与冲击, 2014, 33(20):47-51.

CUI Wei, YAN Bo, YANG Xiao-hui, et al. Numerical investigation on anti-galloping of double bundle conductors with interphase spacers [J]. Journal of Vibration and Shock，2014，33(20)：47-51.

[11] 刘正权，霍锋，魏远航，等.220 kV垂直排列双分裂导线粘连现象分析[J].高电压技术, 2006, 32(11):61-63.

LIU Zheng-quan, HUO Feng, WEI Yuan-hang,et al. Analysis on vertical-arrayed double-bundled transmission line conglutination phenomena of 220kV transmission line [J]. High Voltage Engineering, 2006, 32(11): 61-63.

[12] 樊灵孟，何宏明，邓昌辉.220 kV垂直排列双分裂导线粘连现象分析[J].高电压技术, 2004, 30(6):27-29.

FAN Ling-meng, HE Hong-ming, DENG Chang-hui. Analyses on conglutination phenomena of 220 kV vertical-arrayed double-bundled transmission-lines[J]. High Voltage Engineering, 2004, 30(6):27-29.

[13] 张飚，何小新，喻剑辉，等. 220 kV垂直双分裂导线粘连机理仿真[J].电工技术学报, 2012, 27(5):252-259.

ZHANG Biao, HE Xiao-xin, YU Jian-hui，et al．Mechanism simulation for the causes of 220 kV vertical-arrayed double-bundle transmission line [J]. Transactions of China Electrotechnical Society, 2012, 27(5): 252-259.

[14] Mehta P R, Swart R L.Generalized formulation for electromagnetic forces on current-carrying conductors[J].IEEE Transactions on Power Apparatus and Systems, 1967, 86(2):155-166.

[15] Lilien J L.State of the art of conductor galloping[M]//A complementary document to “Transmission line reference book-Wind-induced conductor motion Chapter 4: Conductor galloping” based on EPRI research project 792.

Effect of electromagnetic force on galloping of twin bundle conductor lines

ZHOULin-shu1,YANBo1,2,ZHAOYang1,ZHANGLiang1

(1. College of Aerospace Engineering, Chongqing University, Chongqing 400044, China;2. State Key Laboratory of Transmission & Distribution Equipment and Power System Safety and New Technology, Chongqing University, Chongqing 400044, China)

Abstract:Based on a numerical method to calculate electromagnetic force between conductors, a finite element to determine electromagnetic force during galloping simulation of twin bundle conductor lines was incorporated into ABAQUS software by means of the user-defined subroutine. This numerical method verified with a numerical example was employed to simulate galloping of twin bundle conductor lines with different span lengths and to analyze the effect of electromagnetic force on their galloping characteristics. The results showed that the effect of electromagnetic force on galloping with a shorter span line is very small, however, the effect on that with a longer span line increases with increase in electric current intensity; therefore, it is necessary to take the effect of electromagnetic force into account when investigating galloping of bundle conductor transmission lines with a longer span.

Key words:electromagnetic force; twin bundle conductor; galloping; numerical simulation

中图分类号:TM753； O39

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.04.023

通信作者严波 男，博士，教授，1965年生

收稿日期：2014-12-23修改稿收到日期：2015-03-04

基金项目：国家自然科学基金(512777186)

第一作者 周林抒 男，博士生，1987年生

E-mail：boyan@cqu.edu.cn