离心式压缩机转子故障识别的EEMD-PCA方法研究

马再超， 温广瑞,2， 张恒辉， 廖与禾

(1.西安交通大学 机械结构强度与振动国家重点实验室，西安　710049； 2.新疆大学 机械工程学院，乌鲁木齐　830047)



离心式压缩机转子故障识别的EEMD-PCA方法研究

马再超1， 温广瑞1,2， 张恒辉1， 廖与禾1

(1.西安交通大学 机械结构强度与振动国家重点实验室，西安710049； 2.新疆大学 机械工程学院，乌鲁木齐830047)

摘要：针对离心式压缩机转子系统振动小，振动信号具有非平稳、非线性和伴随噪声干扰的特点，提出一种总体平均经验模式分解(Ensemble Empirical Mode Decomposition, EEMD)联合主分量分析(Principal Component Analysis, PCA)的故障识别方法。该方法以相关分析结合傅里叶变换选择基本模式分量(Intrinsic Mode Function, IMF)为基础，构造了波动变化性指标以定量识别EEMD的噪声幅值参数；进一步获取各运行状态的14种时域振动评价指标并构造标准化特征数据集后，采用PCA降维法得出不同类型故障的振动模式类别。通过对离心式压缩机转子典型故障的振动信号分析，其结果表明该方法能够在解除信号非平稳非线性干扰的基础上，快速独立地提取信号中的主要振动模式，制定表征不同故障类别的特征数据区域，从而有效提高了离心式压缩机的故障识别能力。

关键词：EEMD;PCA;波动变化性指标;离心式压缩机转子

离心式压缩机，因具有结构简单紧凑，尺寸小，重量轻，振动小，运行平稳等特点，并以其高转速和高功率的高效运行方式，不仅在航空航天、国防建设等高精尖行业得到广泛应用，也同时在石油化工、冶金等国民支柱产业中奠定了其作为动力机械的基础性作用。离心式压缩机本质上属于旋转机械范畴，转子作为其核心部件容易出现各类常见振动故障，一旦发生故障，不但损耗压缩机正常使用寿命，而且降低生产效率[1-4]。因此，快速准确识别离心式压缩机的转子振动状态与故障形式则保障进生产现场的安全稳定。

离心式压缩机转子振动信号往往表现出能量微弱并伴随非线性、非平稳现象及噪声干扰等特点[5-6]，这类问题是学者们长期关注并期待解决的焦点。针对信号的非平稳非线性现象，Huang等[7]提出经验模式分解，初步建立了以瞬时频率度量信号交变特性，以基本模式分量表达信号成分的时频分析方法体系[8]，并迅速在机械设备故障诊断领域得到应用研究。Yu等[9]将EMD和包络分析结合用于滚动轴承故障诊断；Gai[10]采用EMD分析转子起车信号并绘制Bode图；Liu等[11]将基于B样条曲线的EMD和Hilbert谱用于齿轮箱故障诊断。然而，因噪声干扰等异常事件存在，易导致模式混叠问题[12-15]。Wu等[16]提出总体平均经验模式分解，将白噪声辅助经验模式分解，有效抑制了模式混叠现象。该方法也很快在旋转机械故障诊断领域得到应用研究，曹冲锋等[17]采用EEMD研究了转子启动过程中的非平稳信号降噪问题；Yu等[18]采用EEMD研究了转子局部碰摩，并与EMD的效果进行了对比；Lei等[19-20]将EEMD用于转子冲击性碰摩故障诊断研究，并研究了EEMD的加噪方法；陈仁祥等[21]针对转子振动信号的降噪，研究了EEMD的分量选择和加噪次数问题；Zhang等[22]将形态滤波、EEMD、样本熵和灰关联分析结合研究了转子常见故障的分类。以上关于转子振动模式提取的研究都取得一定成绩，但现场实际中面临的非线性、非平稳性和噪声干扰时，EEMD的分析结果仍然存在模式混叠现象，影响了快速并准确区分故障的需求，其主要原因在于噪声幅值参数的定量选取时至今日依然难以解决。另外，由Broomhead等[23]提出的主分量分析，其以最大化表征数据集的方差特性[24]表现出高效性，但其线性本质难以解决非线性因素的干扰。因此，若能构造某种指标定量选取噪声幅值参数，进一步解决EEMD的模式混叠现象，并通过合理的途径将EEMD与PCA结合使用，以解除信号非平稳非线性干扰为前提，则有望采用PCA这类经典线性方法的优势实现离心式压缩机转子常见故障的快速准确识别。

基于以上分析，本研究以仿真离心式压缩机转子系统为研究对象，对基于EEMD的转子振动模式提取和基于PCA的转子故障识别的联合方法进行了探讨，以期为离心式压缩机常见典型故障的识别提供参考。

1基本概念简介

1.1总体平均经验模式分解(EEMD)

EEMD的核心思想是利用白噪声频谱均匀分布的统计特性，为分析信号提供均匀分布的分解尺度；同时利用白噪声的零均值特点，经多次平均后则能抑制噪声的影响，从而有效降低了模式混叠现象，其本质是多次EMD的平均。因此，EEMD的算法步骤[16]可归纳如下：

步骤1在原始信号x(t)中分别加入N次均值为0，幅值标准差为常量的高斯白噪声ni(t)，其式为

xi(t)=x(t)+ni(t)

(1)

式中，i=1,2,…,N。

步骤2对每个xi(t)分别进行EMD分解，得到Ki个IMF分量和余项ri(t),为

(2)

式中，Cij(t)为第i次加入高斯白噪声信号分解得到的第j个IMF，j=1,2,…,Ki。

步骤3将得出的IMF进行总体平均运算，抑制多次加入高斯白噪声的影响，得到真实的IMF和余项r(t),为

(3)

(4)

式中，Cj(t)为原始信号分解后得到的第i个IMF。

步骤4得出K个IMF分量和一个余项r(t),为

(5)

1.2主分量分析(PCA)

PCA是一种通过线性变换进行特征压缩，用尽可能小的维数最大程度地表征原始信息的方法。实现该方法的关键步骤是求解能够最大化表征原始数据集各维度方差特性的投影方向，其计算方法[22]为

Cυ=λυ

(6)

式中，C是原始数据集的协方差矩阵，λ是矩阵C的特征值，ν是与λ对应的特征向量。用最大化方差准则得到矩阵C的N个降序排列特征值λi(i=1,2,…,N)及对应的特征向量νi。从中选择对应特征值较大的若干投影方向，则X对应的输出Y计算方法为

Y=X·γ

(7)

1.3相关分析(CA)

为度量信号与信号之间取值随自变量前后变化的相似性，信号x(t)与y(t)的相关函数[8]定义为

(8)

式中：T为信号x(t)和y(t)的观测时间。Rxy(τ)描述了x(t)和y(t±τ)之间的相关性。实际中常用标准化的相关系数(相关函数)为

(9)

式中，Cxy(τ)为信号x(t)和y(t)的互协方差函数，σx为信号x(t)的标准差，σy为信号y(t)的标准差。

2离心式压缩机转子典型故障识别的EEMD-PCA方法

2.1转子振动模式提取

EEMD的目标是在对噪声解耦的基础上，将信号分解为频率由高到低排列的IMF分量和一个残余项。从转子振动分析的工程经验角度看，信号经EEMD分解得到的高频区域IMF分量为随机噪声，而对于频率过低区域的IMF分量则可能为趋势项、虚假分量或者残余项，将这些无效分量去除，就能得到具有表征转子振动模式特点的IMF分量，既可用于单独分析，也可用于信号重构。对于离心式压缩机的特殊工况条件，使用EEMD得到的IMF分量仍然存在一定程度的频率混叠现象，因此其分量选择旨在最大化保留转子的主要振动模式。

针对转子振动模式表现出强周期性，采用FFT能够发现在某些频率处具有强周期性特点的IMF分量，也能用于检测分量之间是否具有相同频率成分，从而定性判断模式混叠的程度。因此，基于FFT的转子振动模式提取步骤可归纳如下：

步骤1对各IMF分量进行FFT，得到各分量频谱图；

步骤2对比各频谱，找出具有强周期性的分量备选；

步骤3对比各频谱之间有无相同频率成分，定性判断模式混叠程度。

通过上述FFT的思路能够寻找周期性较强的IMF分量，能判断噪声IMF分量，但却无法去除趋势项和虚假分量。采用相关分析的思路能够表现出原始信号与IMF分量之间的关系，也能表现各IMF分量之间的关系，有助于去除无效的IMF分量。因此，基于相关分析的转子振动模式提取步骤可归纳如下：

步骤1计算各IMF分量与原始信号的相关系数，找出与原始信号最相关的若干分量；

步骤2计算各IMF分量之间的相关系数，度量分量之间的模式混叠程度；

步骤3定性剔除与原始信号相关性较小的IMF分量。

2.2EEMD的参数确定

文献[16]指出白噪声对分析信号的影响遵循如式(10)所示的统计规律，即

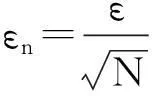
(10)

式中：εn是原始信号与重构结果的偏差，ε是白噪声幅值，N是加噪次数。

由式(10)可以看出信号分解精度与噪声幅值ε成正比，与加噪次数N的开方成反比。为保证分解精度，当ε过小时，难以引起信号局部极值点变化；而当N过大时，将增加算法的复杂程度。因此，文献[16]根据加噪实验推荐一般情况下ε取分析信号标准差的0.2倍。如果信号主要表现为高频特性，则ε可取更小值；如果信号主要表现为低频特性，则ε可取更大值。

离心式压缩机转子振动信号的常见状态主要集中在基频、分频及四倍基频以内的整数频率范围内，属于低频信号。因此，ε可以取适当大于分析信号标准差的0.2倍，并结合前述FFT与相关系数度量分量模式混叠程度的方式来适当修正ε的取值。然而，该方法仍然属于定性判断范畴。由于信号加噪将导致信号的紊乱程度提高和极值点改变，在提高IMF之间的正交性条件下，同时需要保证重构信号相对原始信号的畸变较小。因此，研究中构造了波动变化性指标(Fluctuant Variation Index)如式(11)所示，用于度量原始信号与重构信号对应极值点的波动性变化情况，进而定量判断噪声幅值参数的取值是否合适。由式(11)可见，当FV取较小值时，则认为原始信号经EEMD分解和重构后的波形畸变较小，其对应的噪声幅值参数即为最佳值。

(11)

式中，xp为原始信号峰值，xrms为原始信号均方幅值，yp为重构信号峰值，yrms为重构信号均方幅值。

另外，加噪次数N可以按照文献[16]取100以内即可，文献[21]认为根据转子振动信号的特点取较小的N即可获得较好的分解效果。

2.3典型故障的PCA分类

PCA通过最大化表征数据集方差的正交投影变换描述数据集。因此，具有较高线性度的不同类别数据集将尽可能投影至正交坐标系空间的不同位置。对于前述采用定量方式确定噪声幅值参数的EEMD，其提取的转子振动模式分量达到约束条件下的最佳。因此，可通过下述规划的步骤将转子不同运行状态定量刻画于正交坐标系空间的某些区域：

步骤1将选取的IMF重构转子振动信号；

步骤2计算转子振动信号的均值、方差、标准差、偏斜度、峭度、峰峰值、均方幅值、平均幅值、方根幅值和峰值十种有量纲指标，以及波形指标、峰值指标、脉冲指标、裕度指标四种无量纲指标[8]；

步骤3将几种典型故障的特征评价指标组合形成特征数据集[25]；

步骤4将特征数据集进行PCA分析并选取主要分量，实现可视化操作。

2.4离心式压缩机转子典型故障识别的流程设计

根据2.1～2.3阐述的离心式压缩机转子典型故障识别研究方法，归纳出其总体流程框架如图1所示。

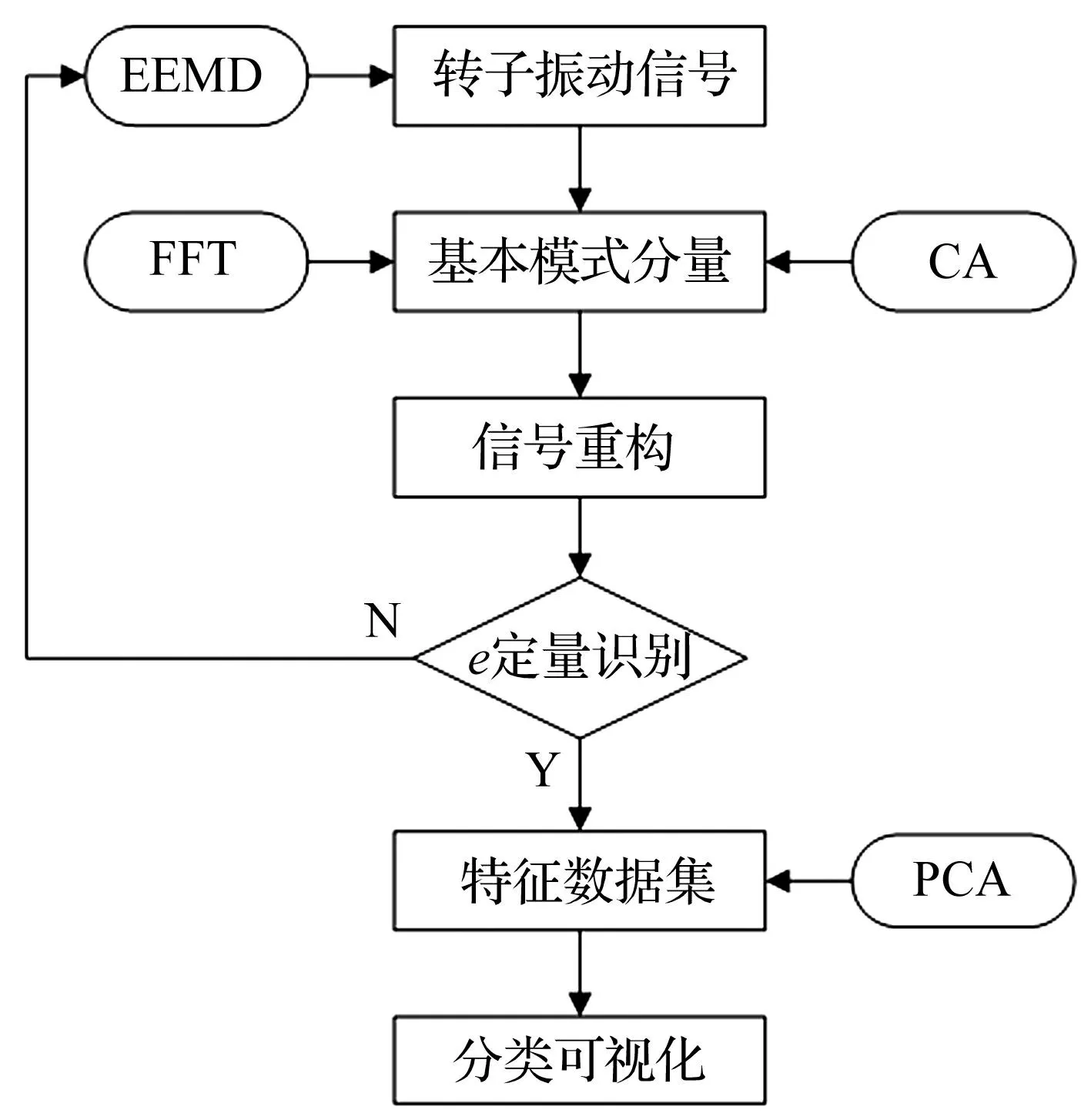
图1　离心式压缩机转子典型故障识别流程Fig.1 Typical faults identification flow of rotor systemin centrifugal compressor

由图1所示流程可归纳出离心式压缩机转子典型故障识别的具体步骤如下：

步骤1设置EEMD初始参数，对转子振动信号进行EEMD分析，得到IMF；

步骤2对IMF进行FFT和CA分析，选择IMF并重构信号；

步骤3定量识别噪声幅值参数的优越性；

步骤4重复步骤1至步骤3直到满足终止条件，得到最佳IMF的重构信号；

步骤5对重构信号提取时域14种特征指标，组合形成特征数据集；

步骤6对特征数据集标准化处理后进行PCA分析，得到分类可视化结果。

3应用情况分析

本研究在离心式压缩机转子实验台上模拟了不平衡，不对中和松动故障。转子实验台由转子系统和振动测试系统组成，如图2所示。转子系统包括转子，质量盘，驱动电机，轴承架和基座；振动测试系统包括六组位移传感器，数据采集模块和上位机。其中的1～4号传感器以45°和135°方向放至并分为两组用于采集转子振动信号；5和6号传感器分别用于测量相位和获取转速。

图2　转子实验台结构Fig.2 Structure of rotor test bench

使用上述转子实验台模拟故障并采集转子振动信号。实验中，采样频率设置为2 048 Hz，采样长度设置为2 048，电机转速设置为4 000 r/min。以不对中运行状态为例，其振动信号及其频谱分别如图3和4所示。

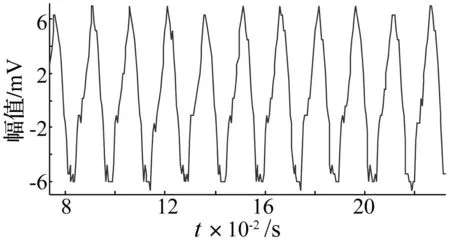
图3　转子不对中振动信号Fig.3 Rotor vibration signal with misalignment

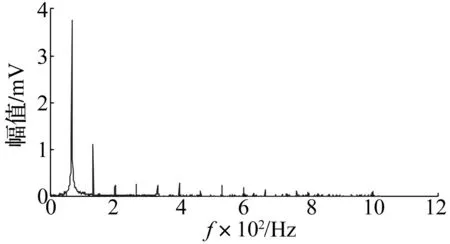
图4　转子不对中振动信号频谱Fig.4 Rotor vibration signal spectrum with misalignment

从转子振动信号及频谱可以看出，基频为主导且存在二倍频，表明此时转子以不对中故障运行。依据2.4归纳的转子系统典型故障识别流程，计算信号的标准差为4.26。因此设置初始参数ε取0.85，N=100，对信号进行EEMD分析，得到的IMF如图5所示。

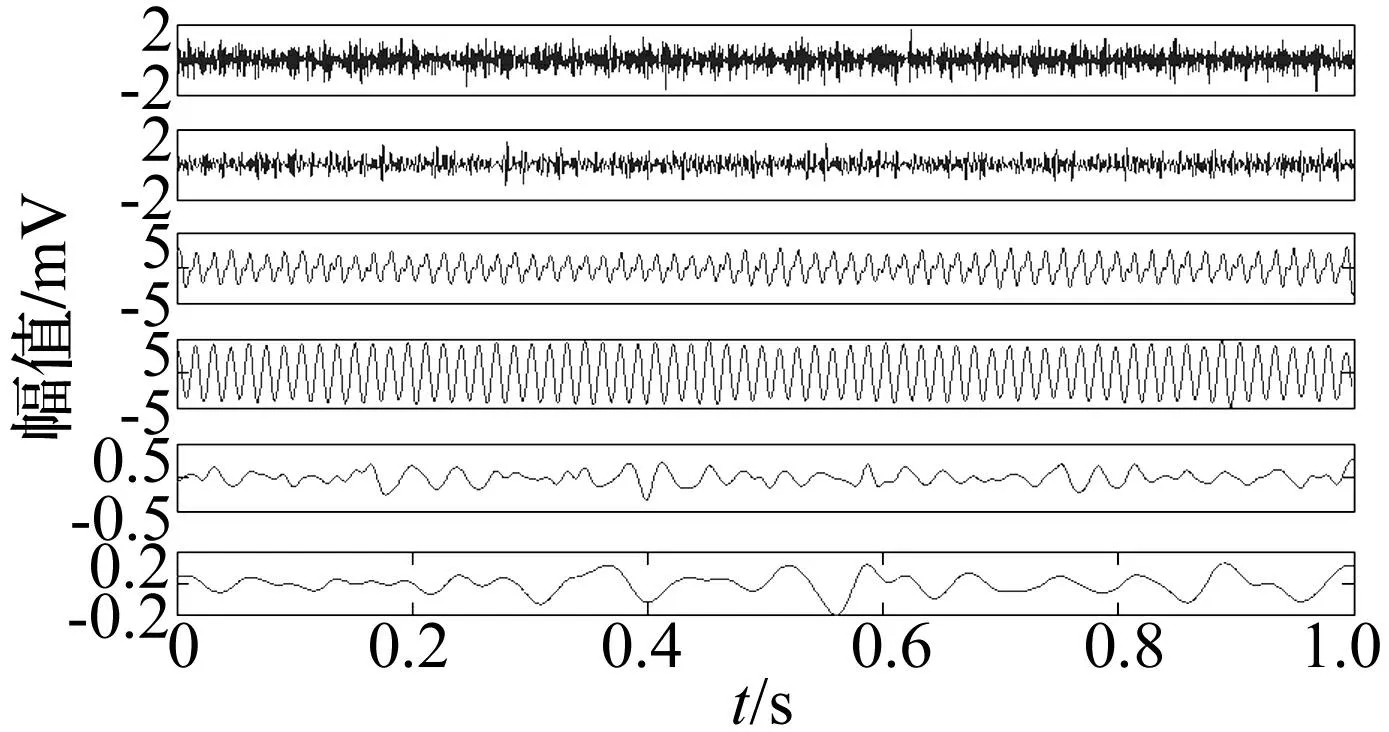
图5　不对中振动信号各IMF(ε=0.85)Fig.5 IMFs of vibration signal with misalignment(ε=0.85)

由图5可以看出，信号的主要振动模式集中于IMF3和IMF4。因此，对前六个IMF分量进行FFT，得到各IMF分量的频谱如图6所示。

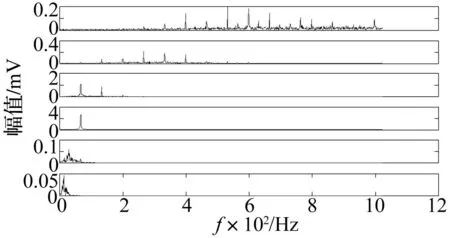
图6　各IMF频谱(ε=0.85)Fig.6 Spectrum of IMFs(ε=0.85)

根据图6频谱可以看出，IMF1和IMF2具有宽频特性，幅值较小，且主要集中在高频处，可以判断为噪声，不予选择；IMF3和IMF4都包含了信号的基频成分，存在模式混叠现象，予以选择；而IMF5和IMF6表现出低频噪声特性，幅值微弱，不予选择。因此，计算各IMF分量与原始信号的相关系数如表1所示。

表1　IMF与信号相关系数(ε=0.85)

由表1可以看出，IMF1和IMF2与原始信号表现出不相关性，可以断定为高频噪声，不予选择；IMF3和IMF4与原始信号表现出很强的相关性，各自代表了一部分振动模式，予以选择；IMF5和IMF6与原始信号表现出不相关性，判断为低频噪声，不予选择。进一步计算IMF3和IMF4之间的相关系数为0.874 3。因此可以看出，IMF3和IMF4之间相关性较大，存在模式混叠。因此将IMF3和IMF4用于信号重构，得到重构信号及其频谱如图7和图8所示。

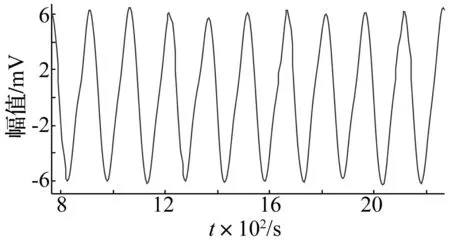
图7　转子不对中重构信号(ε=0.85)Fig.7 Reconstruction signal of rotor with misalignment(ε=0.85)

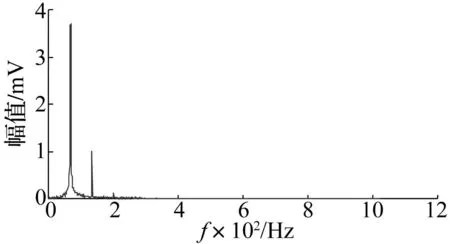
图8　转子不对中重构信号频谱(ε=0.85)Fig.8 Reconstruction signal spectrum of rotor with misalignment(ε=0.85)

由图7和图8可以看出，转子不对中振动模式基本提取出，高频噪声得到抑制但伴随微弱低频噪声且IMF分量存在模式混叠现象。因此，根据转子振动频率主要表现为低频，应取更大ε的原则，调整ε取2.0，重新进行不对中信号的EEMD分析，观察各IMF及其频谱如图9和图10所示。

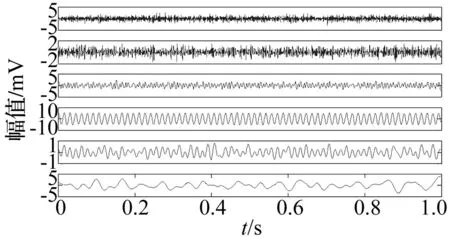
图9　不对中振动信号各IMF(ε=2.0)Fig.9 IMFs of vibration signal with misalignment(ε=2.0)

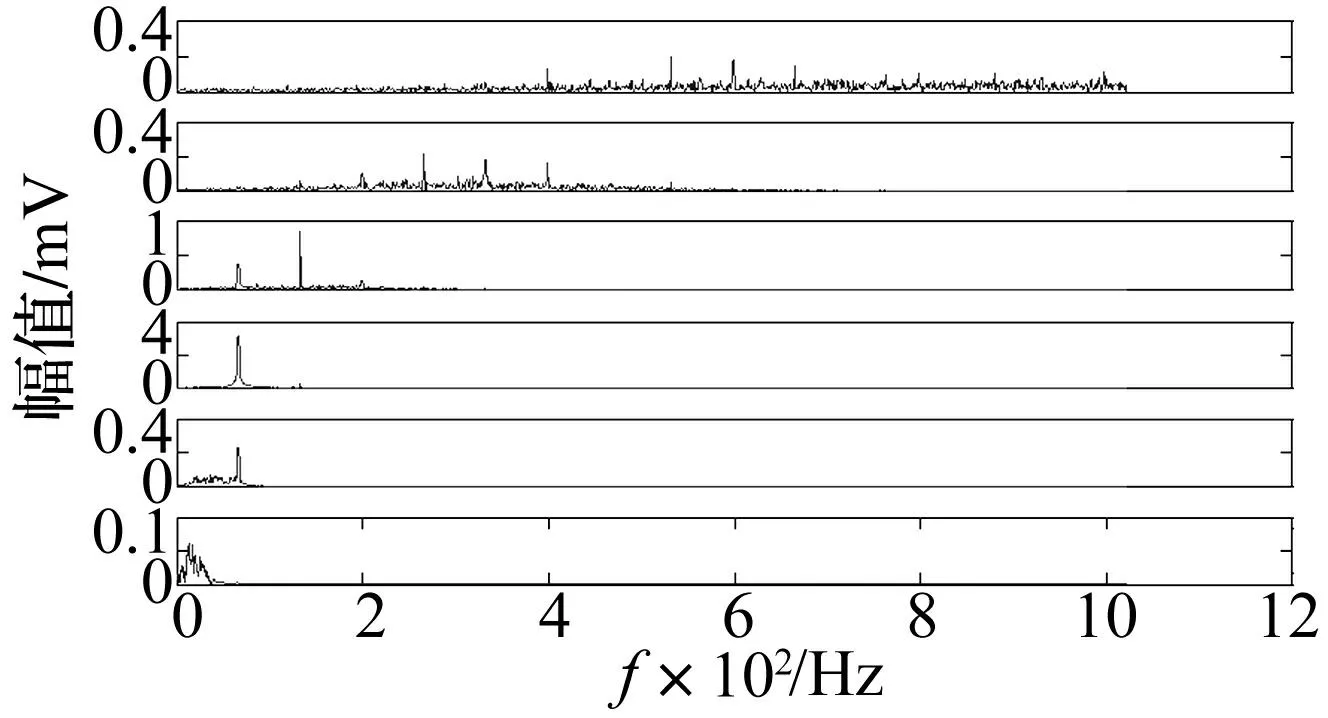
图10　各IMF频谱(ε=2.0)Fig.10 Spectrum of IMFs(ε=2.0)

分别对比图5和图9以及图6和图10可以看出，IMF3表现为二倍频并伴随有轻微一倍频，而IMF4主要表现为一倍频，几乎没有二倍频成分，而IMF5表现出轻微的一倍频且有微弱的低频噪声存在，可见模式混叠现象得到改善。进一步做出前六个IMF与原始信号的相关系数以及各IMF之间的相关系数，分别列于表2和表3所示。

表2　IMF与信号相关系数(ε=2.0)

表3　IMF间相关系数(ε=2.0)

由表2可以看出，IMF1和IMF2与原始信号表现出不相关性，为高频噪声，不予选择；IMF3、IMF4和IMF5与原始信号表现出较强的相关性，各自代表了一部分振动模式，予以选择；IMF6与原始信号表现出不相关性。由表3可以看出，IMF3和IMF4有部分相关性，原因在于IMF3存在微弱基频成分，可见模式混叠的得到改善；IMF3和IMF5的微弱相关性来源于微弱的基频成分；IMF4和IMF5的强相关性来源于主导的基频成分。因此，将IMF3、IMF4和IMF5用于信号重构，得到重构信号及其频谱如图11和图12所示。

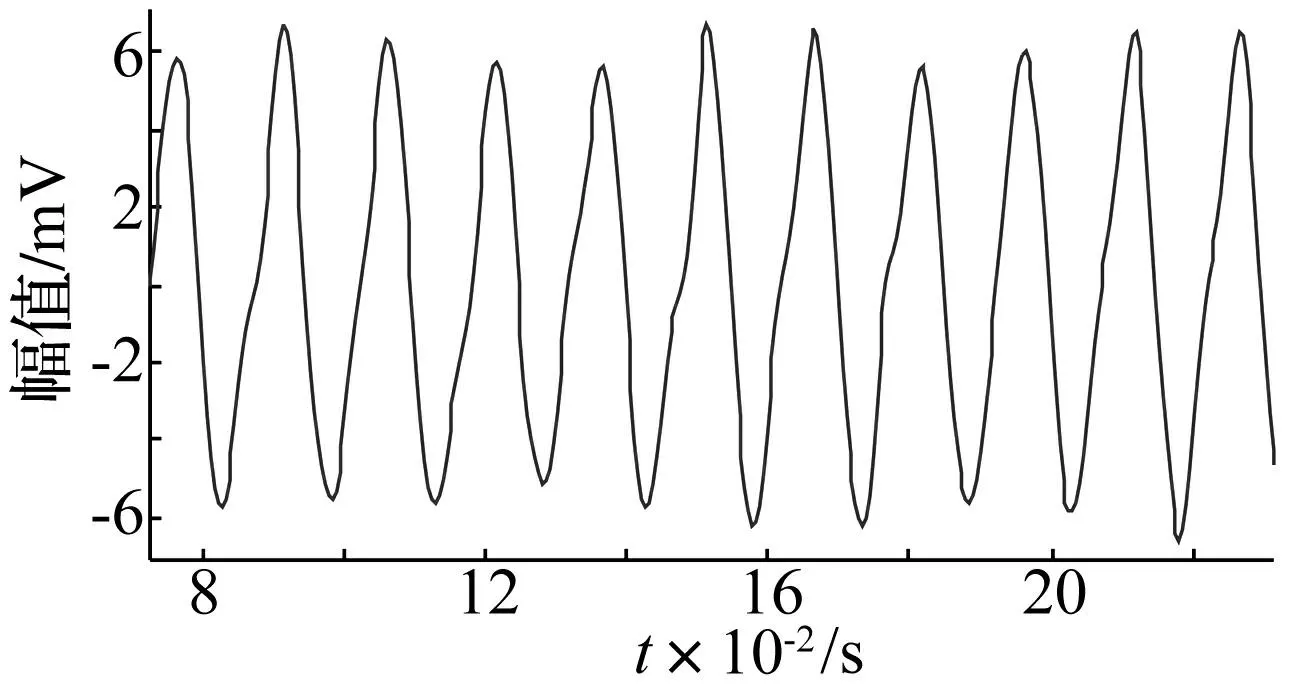
图11　转子不对中重构信号(ε=2.0)Fig.11 Reconstruction signal of rotor with misalignment(ε=2.0)

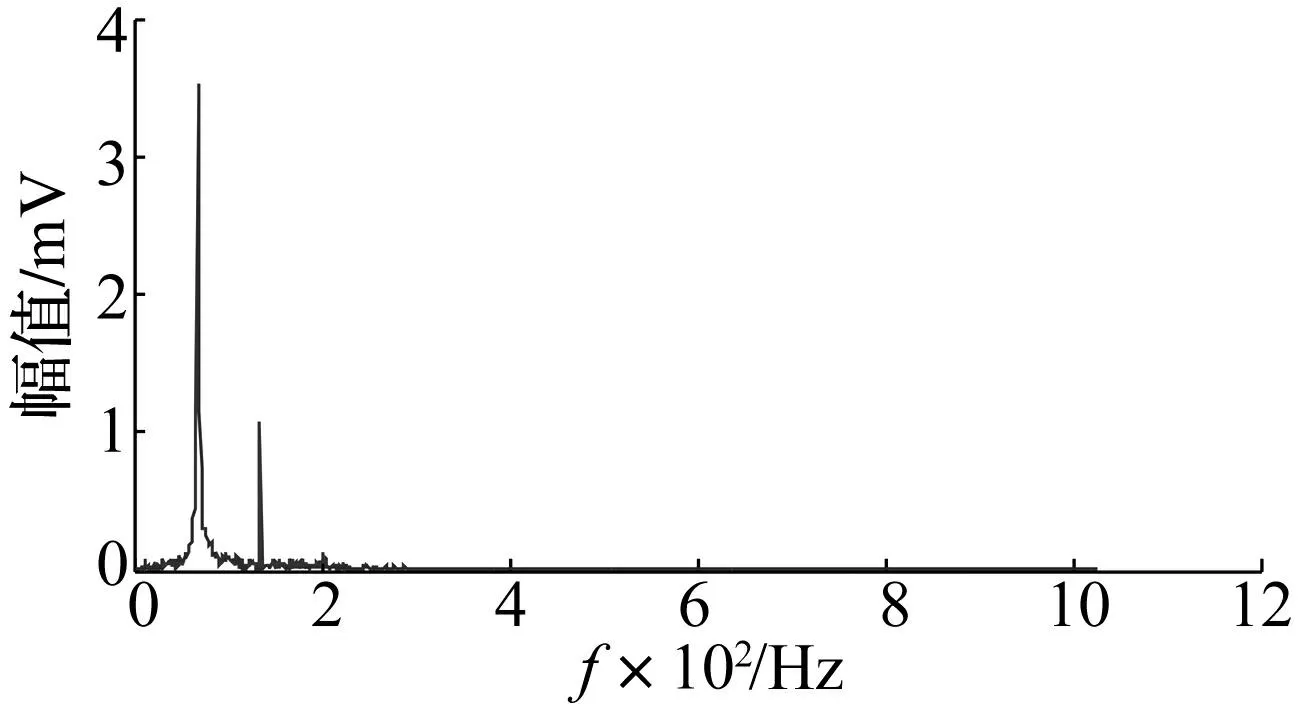
图12　转子不对中重构信号频谱(ε=2.0)Fig.12 Reconstruction signal spectrum of rotor with misalignment(ε=2.0)

对比图11的重构信号全貌和图7的细化结构可以看出，当ε取2.0时，重构信号的波动性较大，主要原因在于噪声幅值过大。而频谱并无明显差异。因此，可以通过FFT结合相关分析的方式逐步迭代判断ε取值，并在迭代过程中不断计算重构信号的波动变化规律，从而在抑制模式混叠的基础上，保证了重构信号的小波动性，得到的IMF分量具有更佳明确的单一振动模式含义。此时，在ε取0.85～2.0的范围之间进行迭代搜索，得到选取的IMF3和IMF4正交性变化规律及重构信号波动性变化规律分别如图13和14所示。

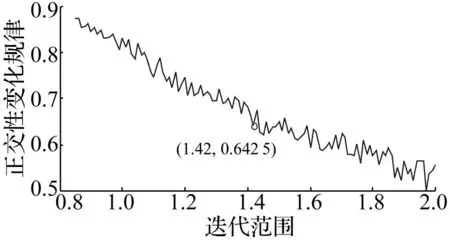
图13　选定IMF的正交性变化规律Fig.13 Orthogonality variation rule of selected IMFs

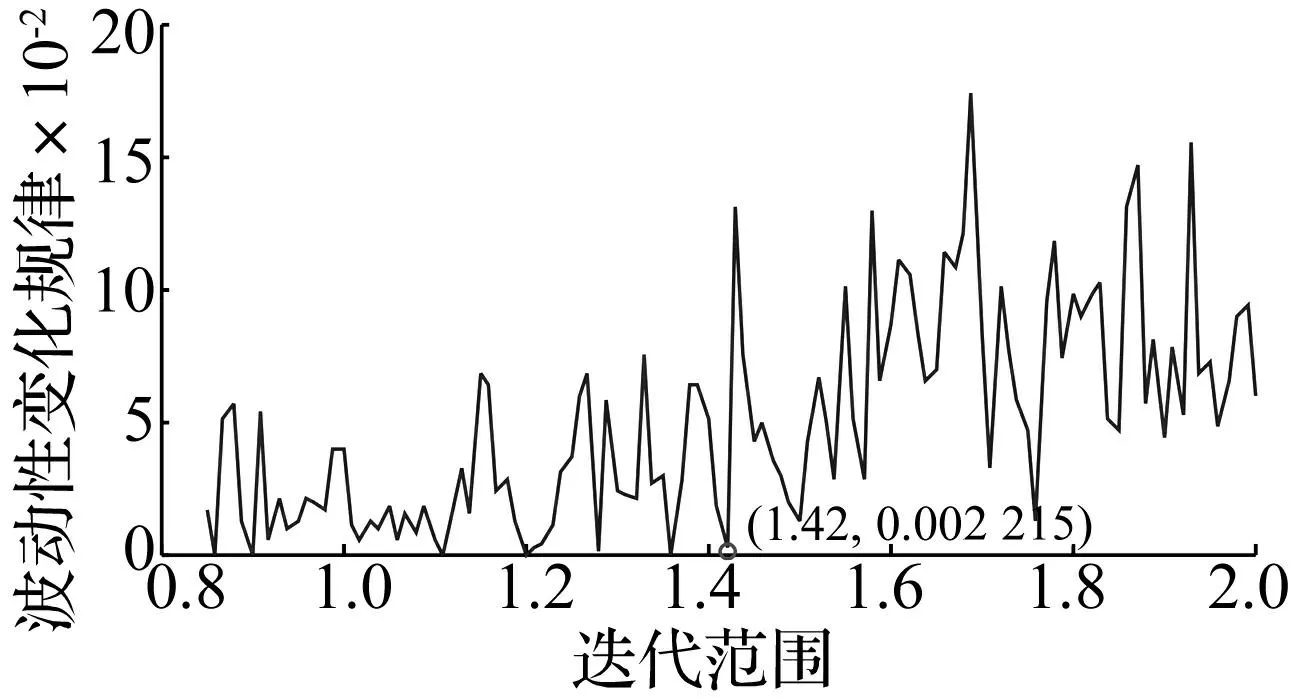
图14　重构信号波动性变化规律Fig.14 Fluctuant variation rule of reconstruction signal

从选定IMF的正交性变化规律可以看出，其正交性取值总体表现出随着噪声幅值参数增加而呈现波动线性下降的趋势，这符合信号噪声加强使得信号间正交性提高的规律。进一步对应观察重构信号波动性变化规律，以横坐标1.40处为分界线，左侧的波动存在接近零值的收敛点；而右侧除红圈标记的1.42处外，找不出能够收敛至接近零值的收敛点，且有波动不断变大的趋势；超出噪声幅值参数取值2.0的部分已不符合文献[16]给出的选取条件。因此，红圈标记的1.42处是图中反映的临界值，而该点也正好与正交性波动变化规律图中红圈标记的1.42极值点处相对应。此时，可以判定当ε取1.42时，分量正交性得到保证且重构信号波动性变化较小，得到的各IMF分量及其频谱如图15和16所示。

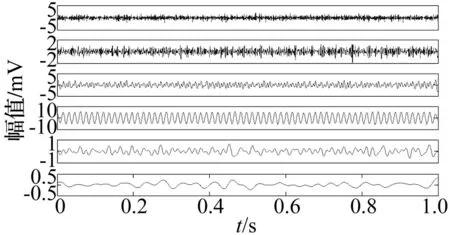
图15　各IMF分量(ε=1.42)Fig.15 IMFs(ε=1.42)

图16　各IMF频谱(ε=1.42)Fig.16 Spectrum of IMFs(ε=1.42)

从图15和图16可以看出，基频的模式混叠现象已经抑制到ε取0.85时的一半，这就基本保证了振动模式的独立化提取，并且IMF5的基频成分极小，可以忽略。通过选取的IMF3和IMF4进行信号重构得到的重构信号和频谱如图17和图18所示。

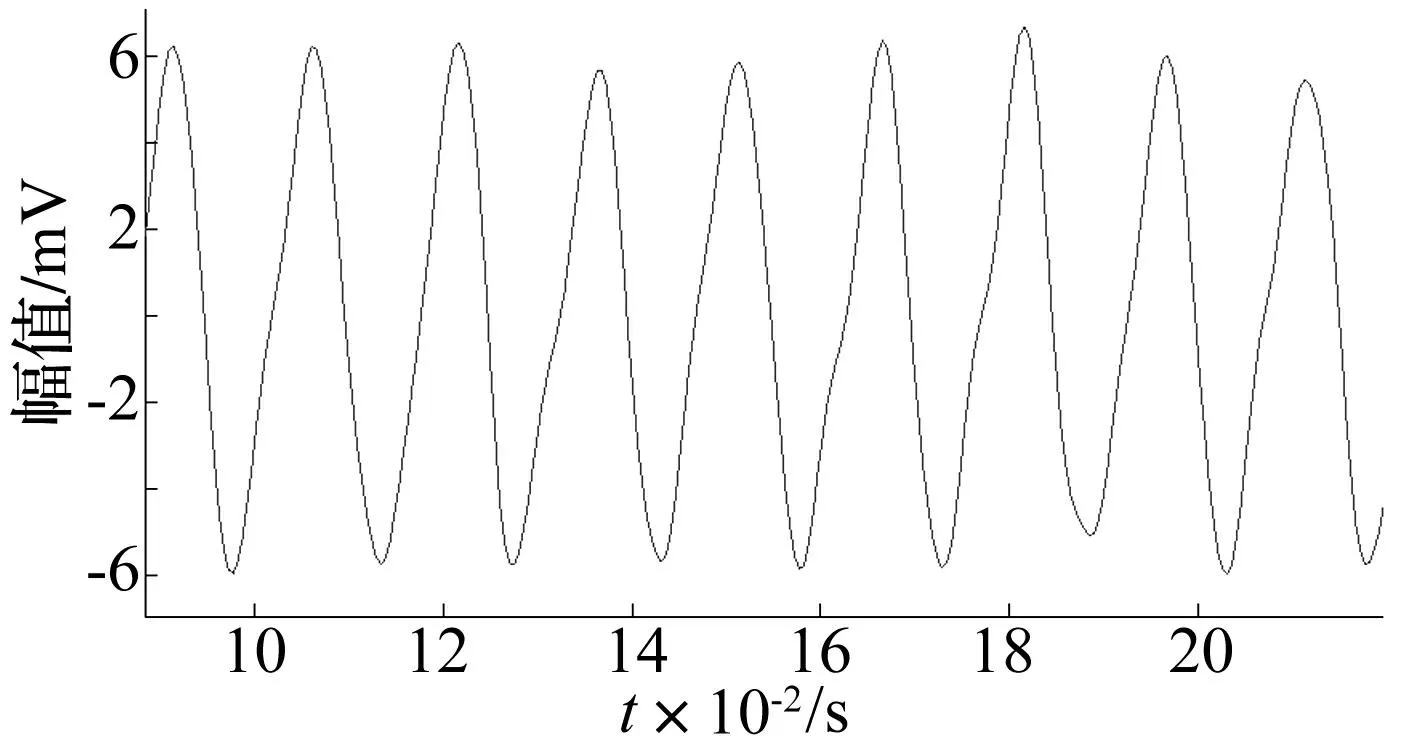
图17　转子不对中重构信号(ε=1.42)Fig.17 Reconstruction signal of rotor with misalignment(ε=1.42)

图18　转子不对中重构信号频谱(ε=1.42)Fig.18 Reconstruction signal spectrum of rotor with misalignment(ε=1.42)

由图17和图18可以看出不对中故障的主要振动模式得到提取，高频噪声消除，时域信号较ε取2.0时的波动性更小。以上结果说明，通过引进本项研究中定义的波动性变化指标，可以将传统EEMD噪声幅值参数的定性学习过程转变为定量学习过程，使得获取的信号分量物理意义更为明确。因此，分别对转子处于正常、不平衡、不对中和松动四种状态进行实验，各采集16组振动信号样本进行EEMD分析并重构原信号，按照第2.4节内容分别提取四种转子运行状态的14种特征指标，构建的标准化特征数据集如表4所示。

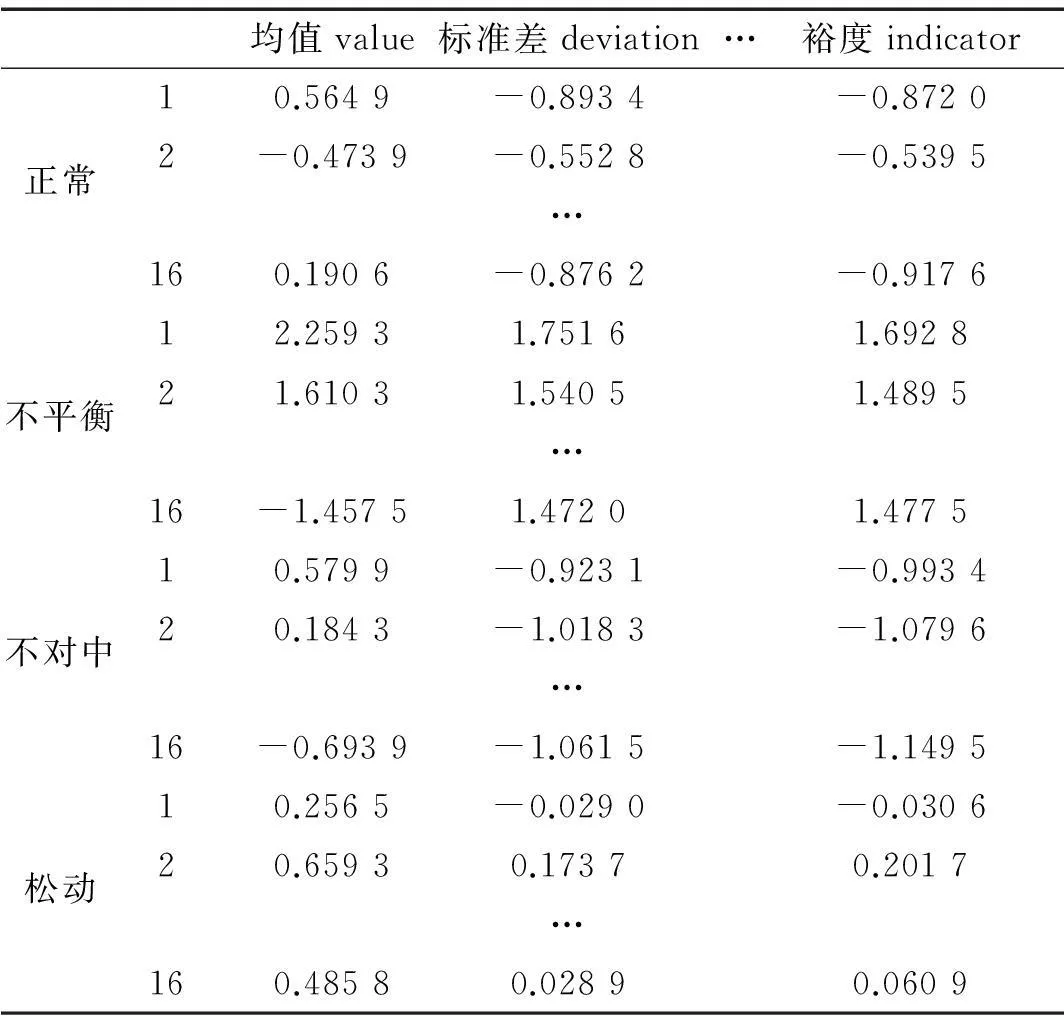
表4　标准化特征数据集

对表4列出的标准化特征数据集进行PCA分析，得到降维数据集，选取对应特征较大的前三个分量进行可视化操作，得到的分类效果如图19所示。同时列出仅采用PCA分析的分类效果如图20所示。

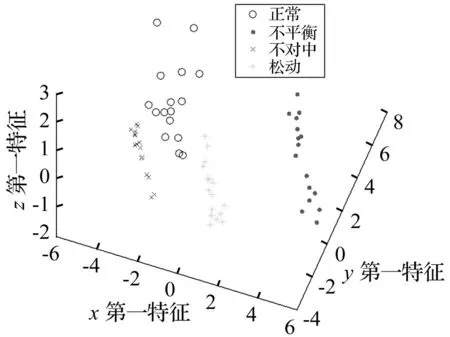
图19　转子运行状态的EEMD-PCA分离效果Fig.19 Separation effect of rotor status withEEMD-PCA

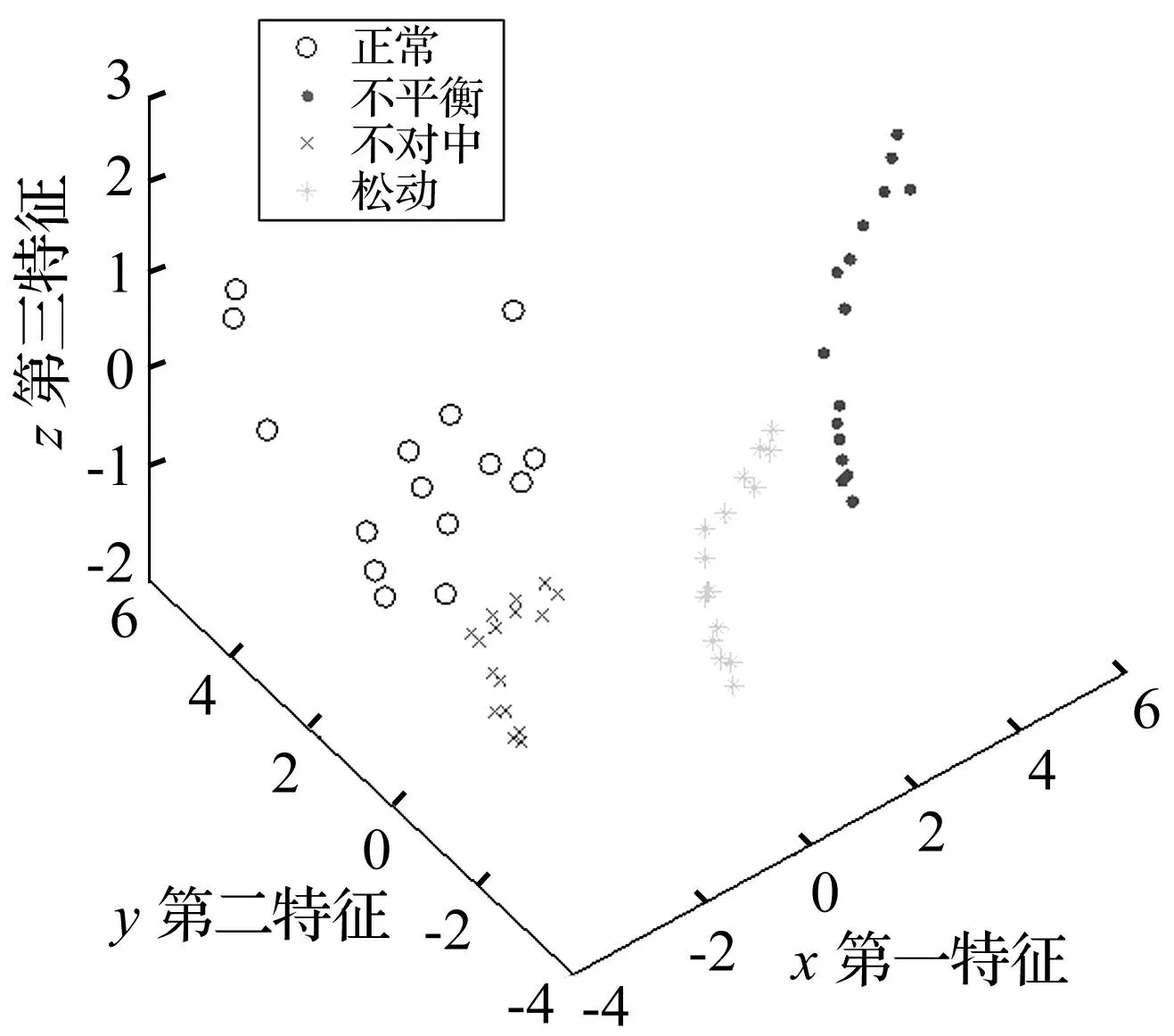
图20　转子运行状态的PCA分离效果Fig.20 Separation effect of rotor status with PCA

对比图19和20可以看出，采用EEMD-PCA和PCA都能将转子四种典型运行状态映射至不同区域。然而，仔细观察两种数据分布情况可以发现，仅仅采用PCA进行映射时，各类别数据集都存在不同程度的弯曲现象，其原因在于实验用转子系统为弱非线性系统，导致原始信号中存在大量高次谐波成分，这些非线性成分使得PCA无法准确线性降维；而经过EEMD进行振动模式提取后的重构信号，其原有的高次谐波成分得到消除，主要的线性振动模式得到提取，此时采用PCA映射数据集将主要呈现线性变化规律。因此，可以想象，当系统具有更强非线性的时候，数据集可视化的弯曲现象将更明显，当振动幅值达到一定程度时，不同类别的数据容易发生交叠，难以找出最优分类超平面。因此，采用本项研究提出的将EEMD与PCA结合分析转子振动信号的方法，能够比较准确地区分转子几种典型运行状态。

4结论

(1) EEMD能够从具有非线性、非平稳性和噪声干扰的离心式压缩机转子振动信号中独立化提取其主要振动模式；

(2) 采用FFT结合相关分析的方法能够辅助选择分量并确定EEMD参数，从而准确独立化提取代表转子主要振动模式的基本模式分量，不仅能重构信号，还有助于研究单一振动模式规律；

(3) 提出的波动性变化指标能够实现转子振动信号EEMD分解过程中的噪声幅值参数定量识别；

(4) EEMD具有解除信号非平稳非线性干扰的效果，不同类别重构信号特征数据集的PCA分离效果表明， EEMD-PCA方法能够快速识别离心式压缩机的几种常见典型故障。

参 考 文 献

[ 1 ] 陈宗华，秦云龙，梁晓刚,等. 石化行业大型离心式压缩机组安全运行研究[J]. 化工装备技术，2005，26(2)：57-64.

CHEN Zong-hua, QIN Yun-long, LIANG Xiao-gang, et al.Safe operation research of large centrifugal compressor unit in petrochemical industry[J]. Chemical Equipment Technology, 2005, 26(2): 57-64.

[ 2 ] 张松梅. 石化行业几种离心式压缩机故障诊断的应用[D]. 大连：大连理工大学，2005.

[ 3 ] 王秋香. K5403离心式压缩机状态监测与趋势预测技术研究[D]. 长沙：湖南大学，2009.

[ 4 ] 徐洪淼. 离心压缩机振动故障分析与处理[D]. 沈阳：沈阳工业大学，2009.

[ 5 ] 曾庆生，王湘江. 基于小波能量谱和粗糙集的离心式压缩机振动故障诊断[J]. 中南大学学报，2009，40(3)：706-710.

ZENG Qing-sheng, WANG Xiang-jiang.Fault diagnosis of centrifugal compressor vibration based on wavelet power spectrum and rough set theory[J]. Journal of Central South University, 2009, 40(3): 706-710.

[ 6 ] Thompson W E. Fluid dynamic excitation of centrifugal compressor rotor vibrations[J]. Journal of Fluids Engineering, 2010,100(1): 73-78.

[ 7 ] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for non-linear and non stationary time series analysis[J].Proceedings of the Royal Society A: Mathematical Physical and Engineering Sciences, 1998, 454: 903-995.

[ 8 ] 何正嘉, 訾艳阳, 张西宁. 现代信号处理及工程应用[M]. 西安:西安交通大学出版社，2007.

[ 9 ] Yu D J, Cheng J S, Yang Y. Application of EMD method and Hilbert spectrum to the fault diagnosis ofroller bearings[J]. Mechanical System and Signal Processing, 2005,19:259-270.

[10] Gai G H. The processing of rotor startup signals based on empirical mode decomposition[J]. Mechanical System and Signal Processing, 2006, 20: 222-235.

[11] Liu B, Riemenschneider S, Xu Y.Gearbox fault diagnosis using empirical mode decomposition and Hilbert spectrum[J]. Mechanical System and Signal Processing, 2006, 20: 718-734.

[12] Huang N E. A new view of nonlinear waves: the Hilbert spectrum[J]. Annual Review of Fluid Mechanics,1999, 31: 417-457.

[13] 赵进平.异常事件对EMD方法的影响及其解决方法研究[J].青岛海洋大学学报，2001，31(6)：805-814.

ZHAO Jin-ping. Study on the effects of abnormal events to empirical mode decomposition method and the removal method for abnormal signal[J]. Journal of Ocean University of Qingdao, 2001, 31(6): 805-814.

[14] Rato R T, Ortigueira M D, Batista A G. On the HHT, its problems, and some solutions[J].Mechanical Systems and Signal Processing,2008,22:1374-1394.

[15] 胡爱军，孙敬敬，向玲.经验模态分解中的模态混叠问题[J].振动、测试与诊断，2011，31(4)：429-434.

HU Ai-jun, SUN Jing-jing, XIANG ling.Mode mixing in empirical mode decomposition[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(4): 429-434.

[16] Wu Z H, Huang N E. Ensemble empirical mode decomposition: a noise assisted data analysis method[J].Advances in Adaptive Data Analysis,2009,1(1):1-41.

[17] 曹冲锋，杨世锡，杨将新.大型旋转机械非平稳振动信号的EEMD降噪方法[J].振动与冲击，2009，28(9)：33-38.

CAO Chong-feng, YANG Shi-xi, YANG Jiang-xin. De-noising method for non-stationary vibration signals of large rotating machineries based on ensemble empirical mode decomposition[J]. Journal of Vibration and Shock,2009, 28(9): 33-38.

[18] Yu Y, Lang H H. Fault Diagnosis of Rotor Rub based on Ensemble EMD[C]//ICEMI’09. 9th International Conference on Electronic Measurement & Instruments, 2009, 2-144-2-148.

[19] Lei Y G, He Z J, Zi YY. Application of the EEMD method to rotor fault diagnosis of rotating machinery[J]. Mechanical System and Signal Processing, 2009,23:1327-1338.

[20] Lei Y G, Li N P, Lin J, et al. Fault diagnosis of rotating machinery based on an adaptive ensemble empirical mode decomposition[J]. Sensors, 2013, 13, 16950-16964.

[21] 陈仁祥，汤宝平，吕中亮. 基于相关系数的EEMD转子振动信号降噪方法[J]. 振动、测试与诊断，2012，32(4)：542-546.

CHEN Ren-xiang, TANG Bao-ping, LÜ Zhong-liang. Ensemble empirical mode decomposition de-noising method based on correlation coefficients for vibration signal of rotor system[J]. Journal of Vibration, Measurement & Diagnosis,2012,32(4): 542-546.

[22] Zhang W B, Zhou Y J, Zhu J X. A new rotor fault diagnosis method based on EEMD sample entropy and grey relation degree[J]. Applied Mechanics and Materials, 2013, (347/348/349/350): 426-429.

[23] Broomhead D S, King G P. Extracting qualitative dynamics from experimental data[J].Physica D, 1986, 20: 217-236.

[24] 李巍华, 史铁林, 杨叔子. 基于非线性判别分析的故障分类方法研究[J]. 振动工程学报，2005，18(2)：133-138.

LI Wei-hua，SHI Tie-lin，YANG Shu-zi. Mechanical fault classification using nonlinear discriminant analysis[J]. Journal of Vibration Engineering, 2005, 18(2): 133-138.

[25] 马再超，赵荣珍，杨文瑛. 转子故障特征数据分类的KPCA-BFDA方法[J]. 振动、测试与诊断, 2013, 33(2): 192-198.

MA Zai-chao, ZHAO Rong-zhen, YANG Wen-ying. KPCA-BFDA for the classification of rotor fault feature data[J]. Journal of Vibration, Measurement & Diagnosis,2013,33(2):192-198.

EEMD-PCA method for rotor fault identification in a centrifugal compressor

MAZai-chao1,WENGuang-rui1,2,ZHANGHeng-hui1,LIAOYu-hei1

(1. State Key Laboratory for Strength and Vibration of Mechanical Structures, Xian Jiaotong University, Xi’an 710049, China;2. School of Mechanical Engineering, Xinjiang University, Wulumuqi 830047, China)

Abstract:Aiming at a centrifugal compressor rotor having small vibration but vibration signals with features of non-stationary, non-linear and interfered with noise, a fault identification method using EEMD together with PCA was proposed for rotor system in a centrifugal compressor. Based on choosing IMFs with correlation analysis combined with FFT, the fluctuant variation index was constructed to recognize amplitude parameters of added noise in EEMD quantitatively. At the same time, 14 kinds of vibration estimated index were calculated to form a standardized feature data set. Consequently, the dimension reduction method of PCA was used to obtain categories of vibration modes with different types of fault. Analysis results of typical fault vibration signals for a rotor system in a centrifugal compressor showed that based on the elimination of non-stationary and non-linear interferences, main vibration modes can be extracted fast and independently, thus feature data regions representing different fault categories can be formulated and the fault identification ability for centrifugal compressor can be improved efficiently with the proposed method.

Key words:EEMD; PCA; fluctuant variation index; rotor of a centrifugal compressor

中图分类号:TH165;TP18

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.04.024

通信作者温广瑞 男，博士后，教授，博士生导师，1976年7月生

收稿日期：2014-08-08修改稿收到日期：2015-07-11

基金项目：国家自然科学基金资助项目(51421004)；国家自然科学基金项目(51365051)；教育部新世纪优秀人才支持计划(NCET-13-0461)；中央高校基本科研业务费专项资金资助

第一作者 马再超 男，博士生，1986年8月生