基于分段多项式的局部特征尺度分解方法及应用

吴占涛，程军圣，曾　鸣，郑近德

(1.湖南大学 汽车车身先进设计制造国家重点实验室，长沙　410082； 2.湖南大学 现代工程训练中心，长沙　4100823.安徽工业大学 机械工程学院，安徽 马鞍山　243002)



基于分段多项式的局部特征尺度分解方法及应用

吴占涛1,2，程军圣1，曾鸣1，郑近德3

(1.湖南大学 汽车车身先进设计制造国家重点实验室，长沙410082； 2.湖南大学 现代工程训练中心，长沙4100823.安徽工业大学 机械工程学院，安徽 马鞍山243002)

摘要：针对局部特征尺度分解(Local Characteristic-scale Decomposition,LCD)方法中两极值点连线在极值点处一阶微分不连续，引起分解精度降低问题，提出新非平稳信号分析方法-基于分段多项式的局部特征尺度分解(Piecewise Polynomial based Local Characteristic-scale Decomposition, PPLCD)。用分段多项式取代LCD中直线连接，且均值曲线插值点由相邻3个同类极值点构成的多项式计算产生。通过仿真信号将PPLCD与LCD对比，结果表明，PPLCD在提高分量正交性、精确性等具有一定优越性；由转子碰摩故障诊断表明该方法的有效性。

关键词：局部特征尺度分解；分段多项式；故障诊断；转子；内禀尺度分量

局部特征尺度分解(Local Characteristic-scale Decomposition，LCD)为新的时频分析方法[1]，能自适应将1个复杂信号分解为若干瞬时频率具有物理意义内禀尺度分量(Intrinsic Scale Component，ISC)之和[2]，获得原始信号完整的时频分布。与经验模态分解[3](Empirical Mode Decomposition，EMD)相比， LCD在减小拟合误差、提高计算速度、抑制模态混淆等有一定优势[4]，已用于信号分析及机械故障诊断等，并取得较好效果[5-7]。EMD与LCD基于筛分的自适应时频分析方法关键为定义合理的均值曲线，该曲线定义优劣直接决定方法的有效性及精确性[8]。

LCD均值曲线插值点由连接两相邻同类极值点的连线计算产生，但存在连线在各极值点处一阶微分不连续会致分解精度降低。为此，本文用分段多项式取代LCD中直线连接，且均值曲线插值点由相邻3个同类极值点构成的多项式计算产生，对LCD均值曲线进行改进，提出基于分段多项式的局部特征尺度分解(Piecewise Polynomial based Local Characteristic-scale Decomposition,PPLCD)，以解决LCD中的不连续问题。

1PPLCD

LCD用线性插值方法计算所有相邻极大(或极小)值点确定的直线及与二者间极值点对应的函数值，进而求出均值曲线插值点，存在连接直线在两极值点处一阶微分不连续问题。采用低次分段多项式拟合相邻3个同类极值点，不仅在与均值曲线各插值点相邻两极值点处一阶微分连续，拟合曲线能较好体现相关极值点数据的变化趋势，且能规避用高次多项式插值可能产生的龙格现象。为此，通过研究PPLCD原理，本文提出基于分段多项式的局部特征尺度分解方法。

1.1PPLCD算法

对实信号x(t)(t>0)，将所有极值点记为(ti，Xi)(i=1,2,…,K)。其中(tk，Xk)、(tk+2，Xk+2)及(tk+4，Xk+4)为相邻极大(小)值点，(tk+1，Xk+1)及(tk+3，Xk+3)为相邻极小(大)值点，(k=1,2,…,K-4)。记函数y(t)在区间[tk,tk+4]部分为yk(t)，(k=1,2,…,K-4)。若yk(t)满足条件

(1)yk(t)≥x(t)或yk(t)≤x(t)；

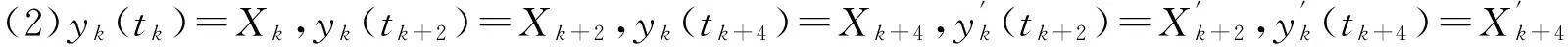
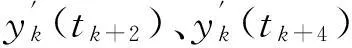
(1)

(2)

设Pk为条件(2)方程组系数矩阵，即

(3)

则该方程组可表示为

MkPk=Nk

(4)

由Mk反除Nk可求得系数矩阵Pk，即

PK=MkNk

(5)

令

(6)

得信号x(t)唯一确定的局部上(下)包络线yk(t)

yk(t)=QkPk，t∈[tk,tk+4]

(7)

可求出yk(t)在两相邻极值点(tk+2，Xk+2)、(tk+4，Xk+4)间极值点对应时刻tk+3处Ak+3点的函数值yk(tk+3)，见图1。

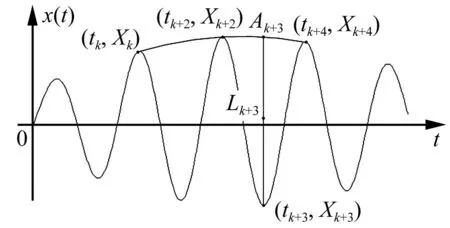
图1　PPLCD方法示意图Fig.1 Schematic of PPLCD method

对应的PPLCD均值曲线插值点Lk+3值为

Lk+3=(Xk+3+yk(tk+3))/2，

(k=1,2,…,K-4)

(8)

由于Lk值下标k从4～K-1，用端点延拓法[9-10]求得L1、L2、L3及LK值。基于确定信号实信号x(t)所有Li值(i=1,2,…,K)，按LCD计算步骤[11]，将原始信号分解为n个ISC分量与1个趋势项un(t)之和，即

(9)

1.2仿真信号分析

为说明PPLCD方法的优越性，考虑式(9)混合信号

x(t)=x1(t)+x2(t)，(t∈[0,1])

(10)

式中：x1(t)=(1+0.35sin(25πt))sin(200πt+60πt2)，x2(t)=sin(85πt)，其时域波形见图2。

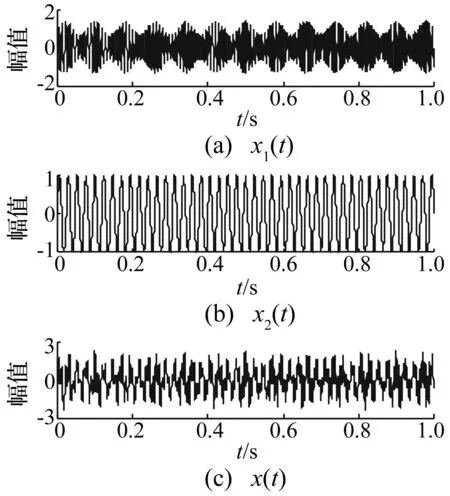
图2　仿真信号x(t)及各成分时域波形Fig.2 The time domain waveforms of simulation signal x(t) and its componments

分别采用LCD、PPLCD对仿真信号x(t)进行分解，结果见图3、图4，两种方法分解绝对误差见图5。分解绝对误差定义为分解所得ISC分量与真实分量之差绝对值。图3中i1、i2、r2分别表示第1、2个ISC分量及剩余项，图4中I1、I2、R2分别表示第1、2个ISC分量及剩余项，图5中E1、E2分别表示两种方法第1、2个ISC分量分解绝对误差。由图3～图5看出，PPLCD分解结果较理想，分解分量与真实分量非常接近，分解绝对误差较小。LCD分解结果虽亦较理想，但分量i1出现局部波形失真(图3实线圈部分)，分量i2幅值与真实分量幅值相差较大，且两分量绝对误差略大于PPLCD。

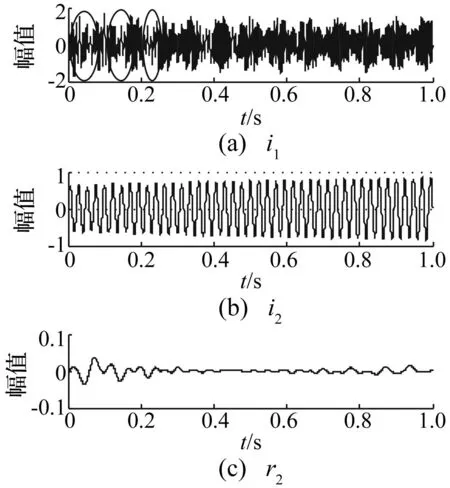
图3　仿真信号x(t)的LCD分解结果Fig.3 The LCD decomposition results of simulation signal x(t)

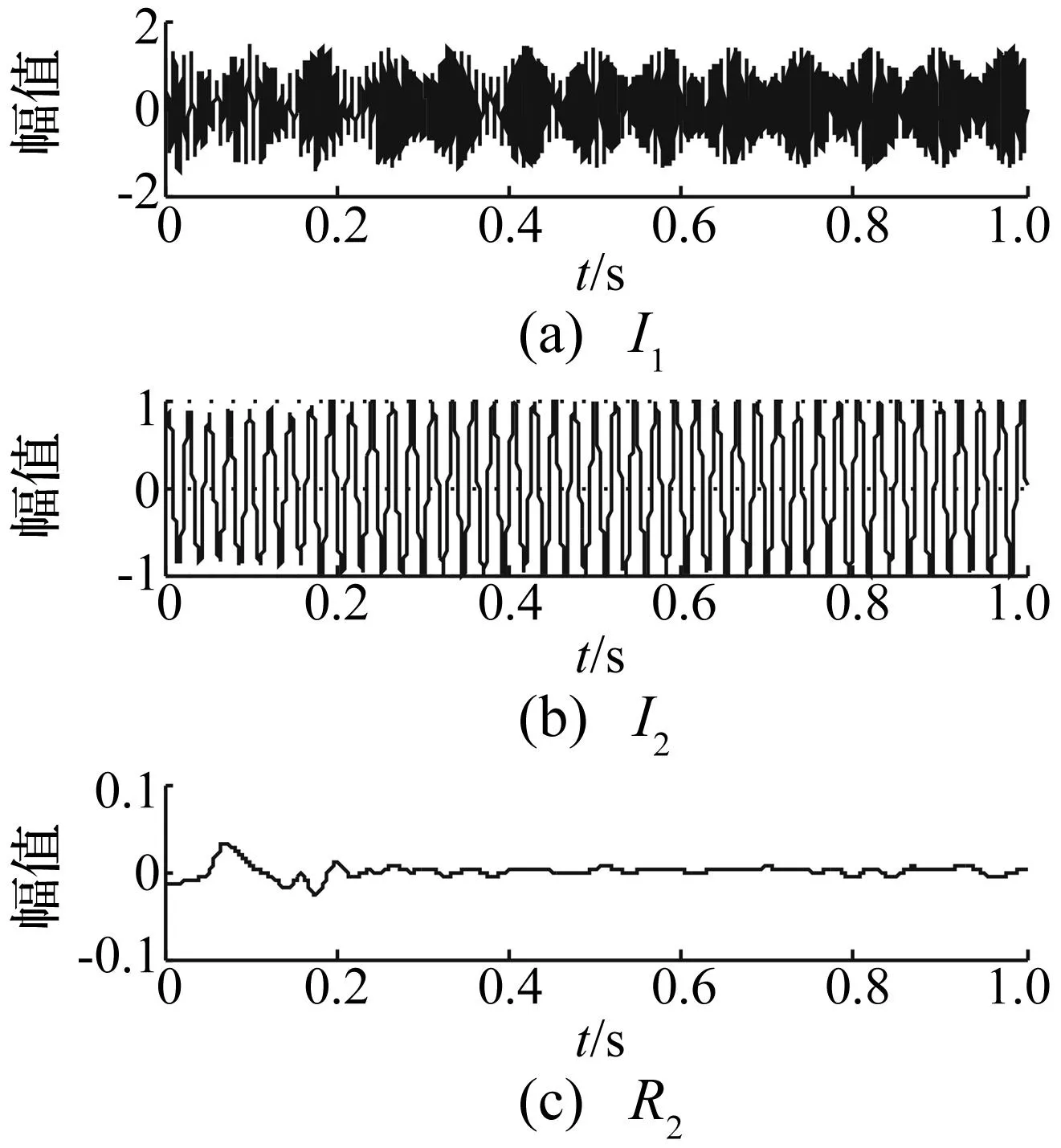
图4　仿真信号x(t)的PPLCD分解结果Fig.4 The PPLCD decomposition results of simulation signal x(t)

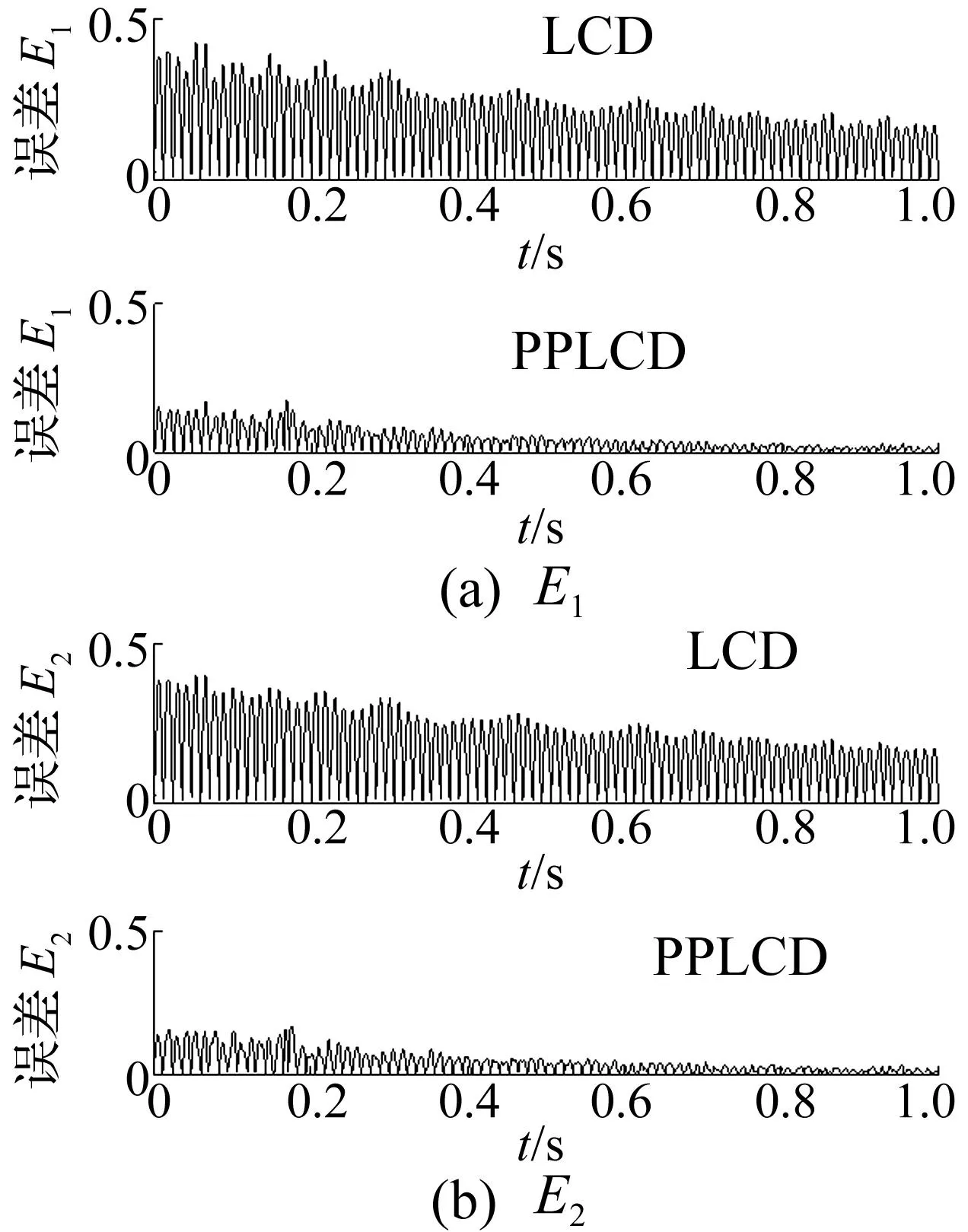
图5　两种方法分解仿真信号x(t)绝对误差Fig.5 The absolute error of the LCD and PPLCD

为比较两种方法的分解效果，考察其分解正交性指标(IO)[12]及所得前两分量与真实分量均方根误差(RMSE)及相关系数(CC)[12]。IO值越小表示所有分解分量间正交性越好；RMSE值越小表示分解误差越小；CC值越大表示分解准确性越高。各评价指标值见表1，其中RMSEi、CCi分别表示第i个分解分量与对应的真实分量均方根误差及相关系数，i=1,2。由表1看出，与LCD方法相比，PPLCD方法正交性指标及均方根误差指标值均最小，相关系数指标值均最大，说明PPLCD的正交性、精确性等具有一定优越性。

用希尔伯特变换法提取两种分解法分解的前两分量瞬时频率及瞬时幅值，结果见图6、图7。由两图看出，无论瞬时频率或幅值，I1均较i1更准确，波动性更小；i2的瞬时频率与I2结果接近，效果均较好，但I2的瞬时幅值较i2更准确。进一步说明PPLCD分解方法有效、可行。

表1　两分解方法评价指标

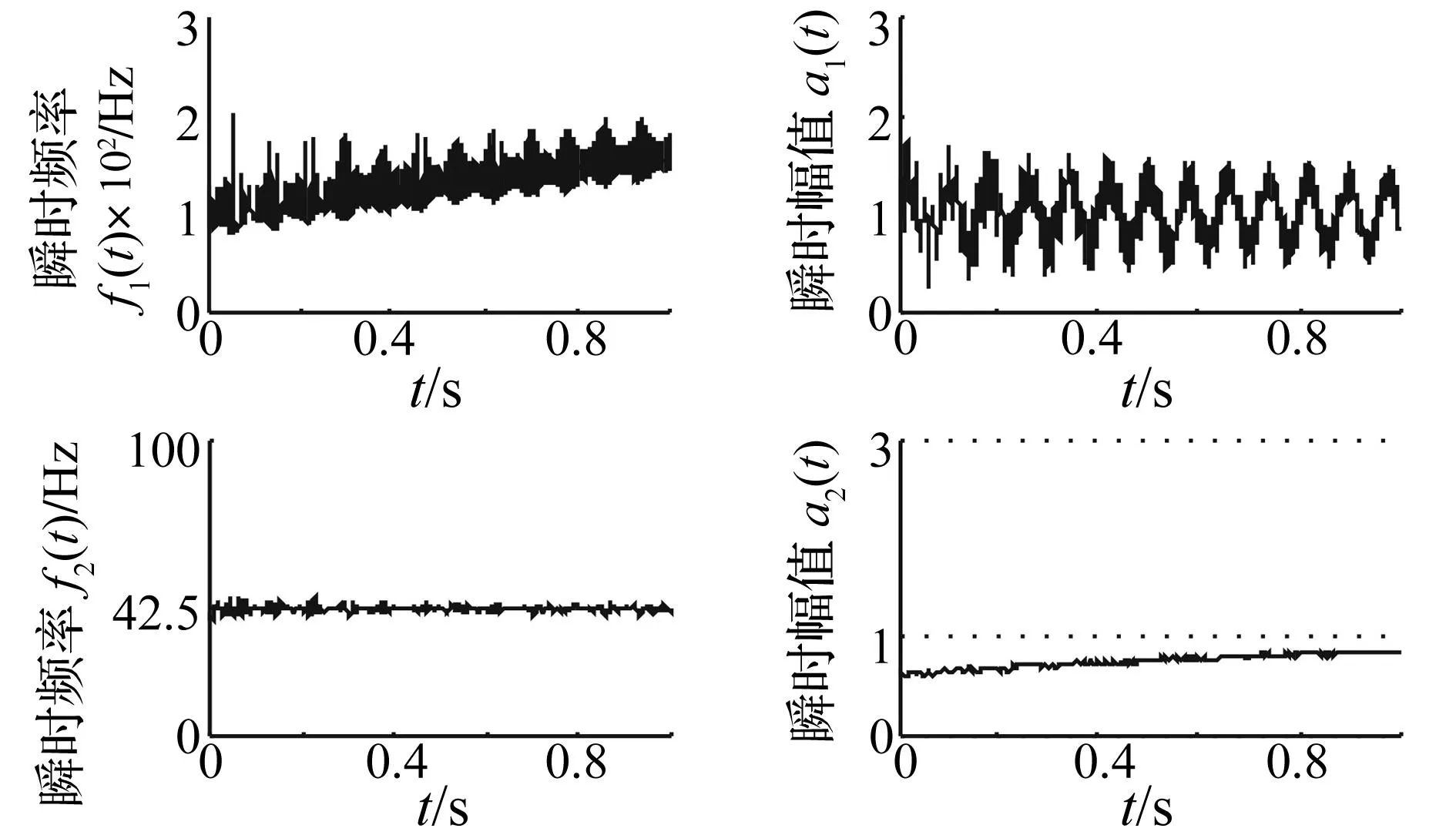
图6　由LCD所得分量i1、i2瞬时频率及幅值Fig.6 IFs and IAs of ISCi calculated by LCD

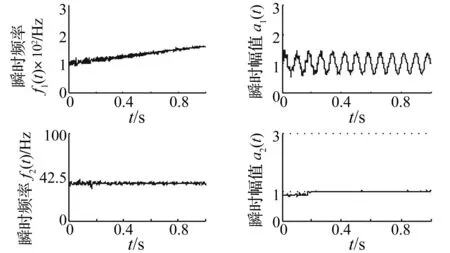
图7　由PPLCD所得分量I1、I2瞬时频率及幅值Fig.7 IFs and IAs of ISCi calculated by PPLCD

2应用实例

为说明PPLCD方法的有效性、实用性，将其用于具有碰摩故障的转子振动位移实验信号分析。实验采样频率fs=2 048 Hz，采样时长0.5 s，转速3 000 r/min，转频fr=50 Hz。实验数据时域波形见图8，幅值谱见图9。转子产生碰摩故障时其振动位移信号会产生1个以转频为幅值调制频率的高频碰摩分量[13-14]，由图8可看出高频碰摩信号淹没于强大背景信号中。而图9中主要为与转频fr相关的基频分量，看不出碰摩故障信息。

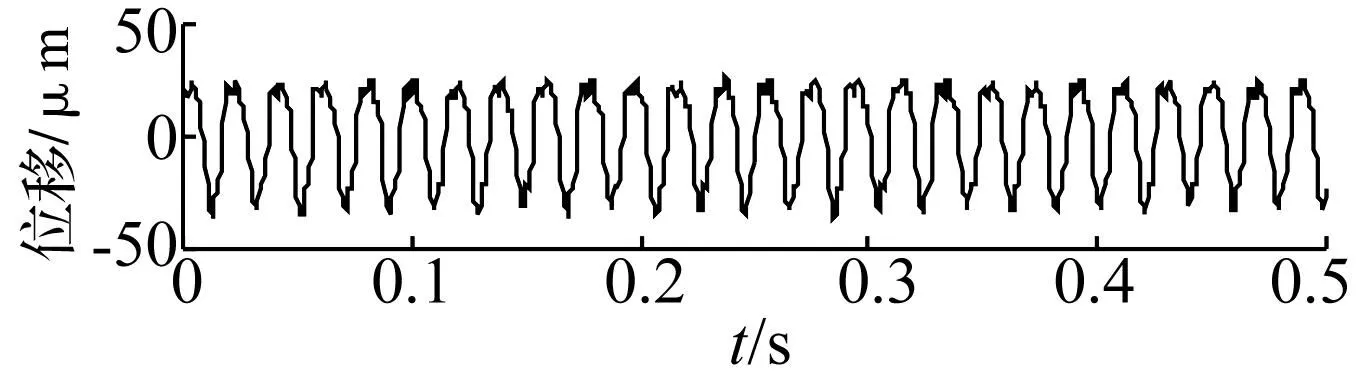
图8　实验数据时域波形Fig.8 The time domain waveforms ofexperimental data

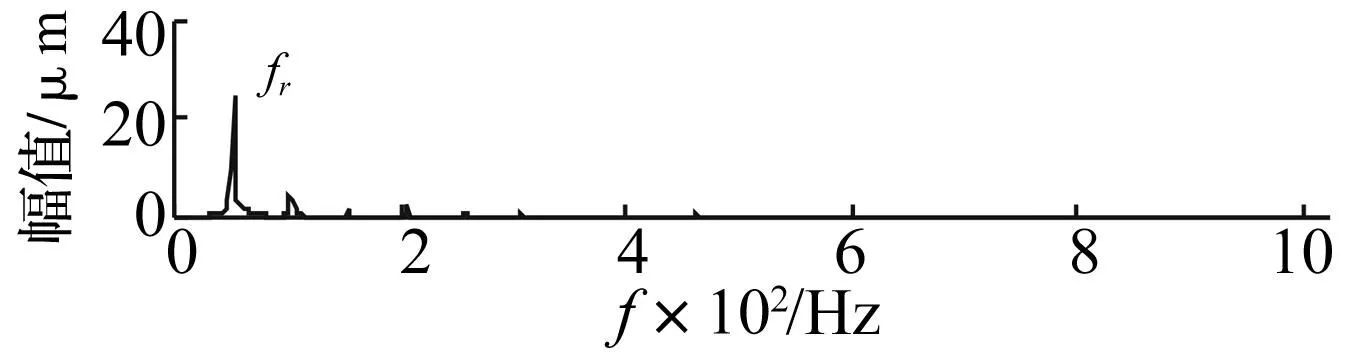
图9　实验数据幅值谱Fig.9 The amplitude spectrum of experimental data

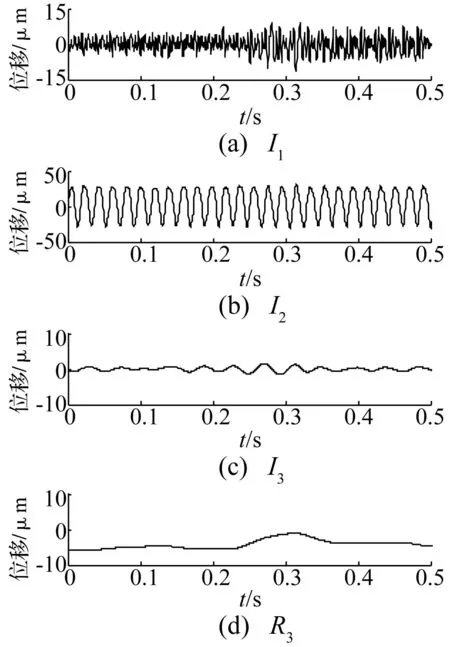
图10　实验数据的PPLCD分解结果Fig.10 The PPLCD decomposition results of experimental data

为提取高频碰摩信息，分别采用PPLCD及LCD对实验数据进行分解，结果见图10、图11。PPLCD、LCD分解所得第1个分量I1、i1的包络谱见图12、图13。由图10看出，PPLCD方法对实验数据分解的第1分量I1调制特征明显。由图12可看到明显的转频及其倍频成分，说明I1的调制波频率与转频fr相同，此由转子每旋转一周动件均与静件摩擦所致[15-16]；I1分量主要成分为碰摩信号，亦会包含噪声。由图11看出，LCD方法对实验数据分解的第1分量i1亦有调制特征，而图13包络谱虽亦能看出转频及其倍频成分，但幅值较小，无PPLCD方法明显，且出现两个较明显的不明低频分量。

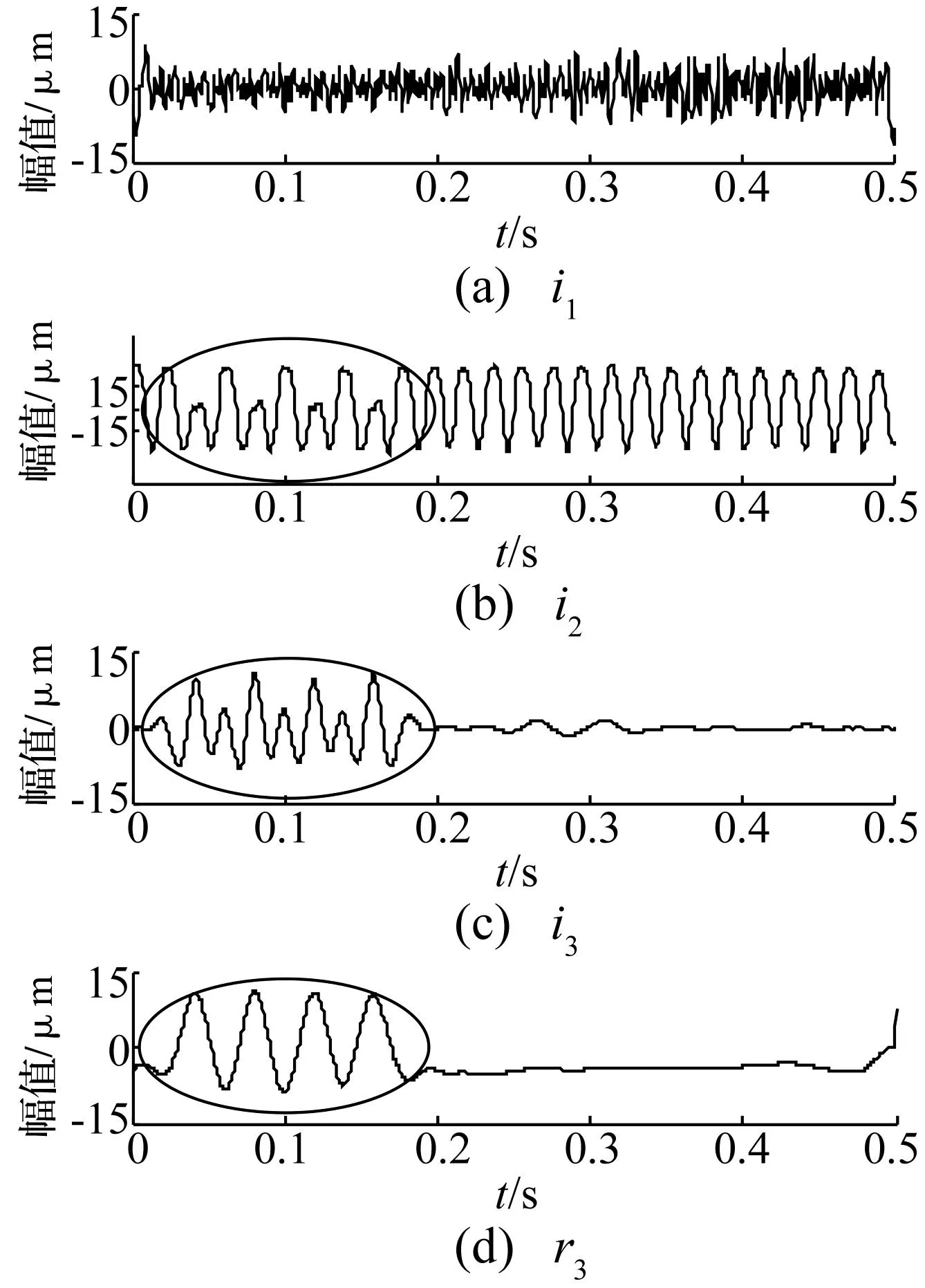
图11　实验数据的LCD分解结果Fig.11 The LCD decomposition results of experimental data

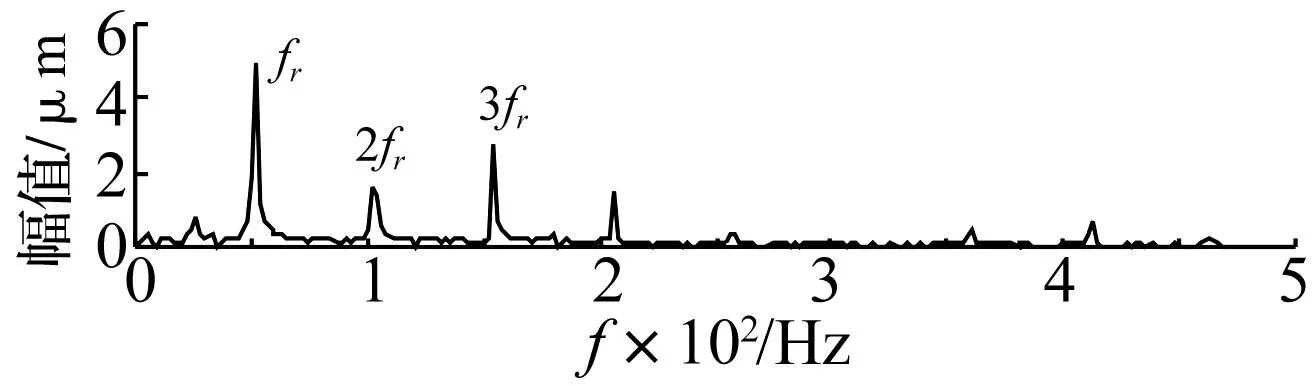
图12　PPLCD第1分量包络谱Fig.12 The envelope spectrum of calculated by PPLCD

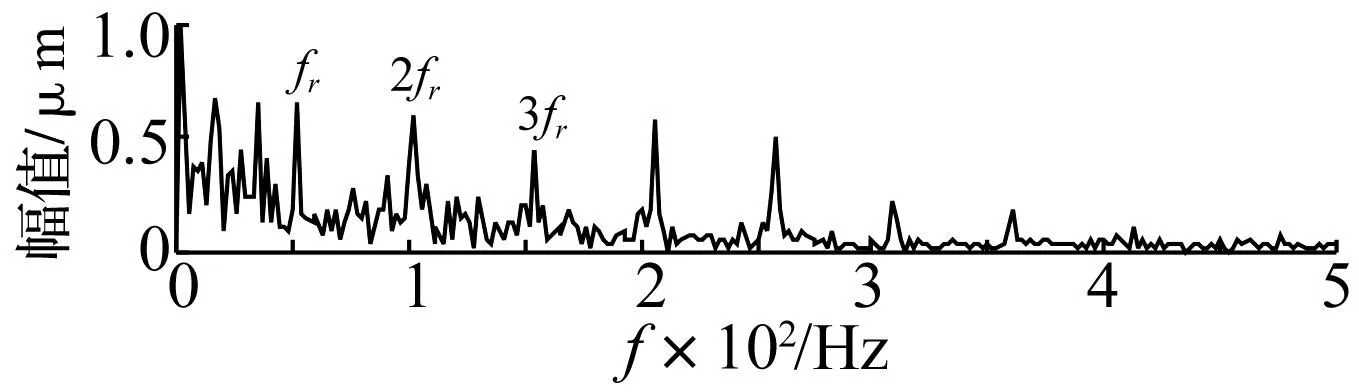
图13　LCD第1分量包络谱Fig.13 The envelope spectrum of calculated by LCD

PPLCD的分量I2、I3为与转频有关的背景信号，其幅值谱见图14。由图14看出，I2、I3所含主要频率成分为转频的1倍频及1/2倍频。剩余信号R3为低频噪声。图11中LCD分量i2、i3、r3出现严重的波形失真(实线所圈部分)，其幅值谱见图15。由图15看出，分量i2的主要频率为转频的1倍频，同时也出现转频的1/2倍频；分量i3主要频率成分为转频的1/2倍频、1倍频。由于LCD对实验数据分解时分量i2、i3出现波形失真，分别混入转频1/2倍频、1倍频的频率成分，可见与图11分解结果一致。

图14　PPLCD分量I2、I3幅值谱Fig.14 The amplitude spectrum of I2 and I3 calculated by PPLCD

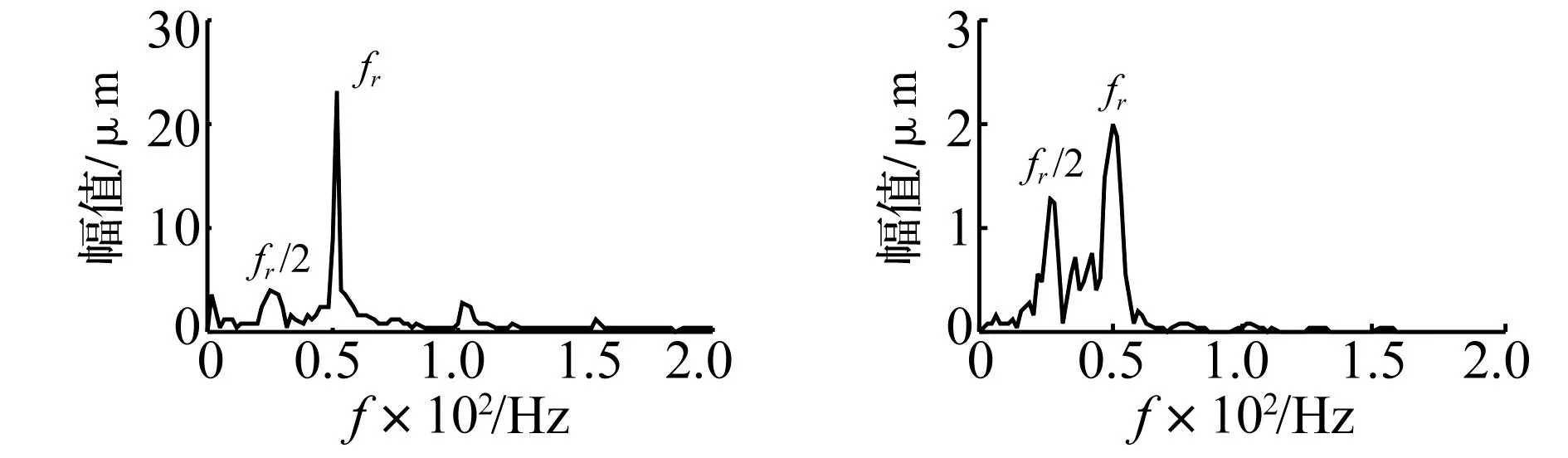
图15　LCD分量i2、i3幅值谱Fig.15 The amplitude spectrum of i2 and i3 calculated by LCD

由此可认为，PPLCD能更有效分离出实验数据中与碰摩相关的高频分量，便于提取故障信息，实现转子系统故障诊断。而该方法亦有不足之处，也存在模态混淆等问题，尚待进一步完善。

3结论

通过基于分段多项式局部特征尺度分解(PPLCD)对仿真信号及实验数据分析，结论如下：

(1)PPLCD所得分量更具有物理意义，分量与真实值间误差更小。

(2)PPLCD无需预设运行参数，为自适应的信号分析方法。

(3)PPLCD能有效地提取振动信号中与故障特征有关的分量，且效果优于LCD。

参 考 文 献

[ 1 ] 程军圣,郑近德,杨宇. 一种新的非平稳信号分析方法-局部特征尺度分解法[J]. 振动工程学报, 2012, 25(2): 215-220.

CHENG Jun-sheng,ZHENG Jin-de,YANG Yu. A nonstationary signal analysis approach-the local characteristic-scale decomposition method[J]. Journal of Vibration Engineering, 2012, 25(2): 215-220.

[ 2 ] 杨宇,曾鸣,程军圣. 局部特征尺度分解方法及其分量判据研究[J]. 中国机械工程, 2013, 24(2):195-201.

YANG Yu, ZENG Ming, CHENG Jun-sheng. Research on local characteristic-scale decomposition and its stopping criteria[J]. China Mechanical Engineering, 2013, 24(2):195-201.

[ 3 ] Lei Y, Lin J, He Z, et al. A review on empirical mode decomposition in fault diagnosis of rotating machinery[J]. Mechanical Systems and Signal Processing,2013,35(1):108-126.

[ 4 ] 杨宇,曾鸣,程军圣. 局部特征尺度分解方法及其分解能力研究[J]. 振动工程学报, 2012, 25(5):602-609.

YANG Yu, ZENG Ming, CHENG Jun-sheng. Research on local characteristic-scale decomposition and its capacities[J]. Journal of Vibration Engineering, 2012, 25(5):602-609.

[ 5 ] Zheng Jin-de, Cheng Jun-sheng, Yang Yu. A rolling bearing fault diagnosis approach based on LCD and fuzzy entropy[J]. Mechanism and Machine Theory, 2013, 70: 441-453.

[ 6 ] 程军圣,杨怡,杨宇. 局部特征尺度分解方法及其在齿轮故障诊断中的应用[J]. 中国机械工程学报,2012,48(9):64-71.

CHENG Jun-sheng, YANG Yi, YANG Yu. Local characteristic-scale decomposition method and its application to gear fault diagnosis[J]. Journal of Mechanical Engineering, 2012, 48(9): 64-71.

[ 7 ] 郑超,郭奇,郭丽杰,等. 基于局部特征尺度分解的旋转机械故障欠定盲源分离方法研究[J]. 燕山大学学报,2014, 38(2): 168-174.

ZHENG Chao, GUO Qi, GUO Li-jie, et al. Underdetermined blind source separation method of rotating machinery faults based on local characteristic-scale decomposition[J]. Journal of Yanshan University, 2014, 38(2):168-174.

[ 8 ] Zheng Jin-de, Cheng Jun-sheng, Yang Yu. Generalized empirical mode decomposition and its applications to rolling element bearing fault diagnosis[J]. Mechanical Systems and Signal Processing, 2013, 40(1): 136-153.

[ 9 ] Cheng J, Yu D, Yang Y. Application of support vector regression machines to the processing of end effects of Hilbert-Huang transform[J]. Mechanical Systems and Signal Processing, 2007, 21(3): 1197-1211.

[10] Rilling G, Flandrin P, Goncalves P. On empirical mode decomposition and its algorithms[C]//IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing NSIP. Grodo, Italy,2003.

[11] 程军圣,郑近德,杨宇. 基于局部特征尺度分解的经验包络解调方法及其在机械故障诊断中的应用[J]. 机械工程学报, 2012, 48(19): 87-99.

CHENG Jun-sheng, ZHENG Jin-de, YANG Yu. Empirical envelope demodulation approach based on local characteristic-scale decomposition and its applications to mechanical fault diagnosis[J]. Journal of Mechanical Engineering, 2012, 48(19): 87-99.

[12] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995.

[13] 马辉,太兴宇,牛和强,等. 转定子静态不对中条件下碰摩故障仿真[J]. 振动工程学报, 2013, 26(2):260-268.

MA Hui, TAI Xing-yu, NIU He-qiang, et al. Rub-impact fault simulation of a rotor system under static misalignment conditions[J]. Journal of Vibration Engineering,2013,26(2):260-268.

[14] Yang Y, Cheng J S, Zhang K. An ensemble local means decomposition method and its application to local rub-impact fault diagnosis of the rotor systems[J]. Measurement, 2012, 45(3): 561-570.

[15] 韩清凯,于涛,王德友,等. 故障转子系统的非线性振动分析与诊断方法[M]. 北京:科学出版社, 2010:37-65.

[16] 闻邦椿,武新华,丁千,等. 故障旋转机械非线性动力学的理论与试验[M]. 北京:科学出版社, 2004:112-135.

Piecewise polynomial based local characteristic-scale decomposition and its application

WUZhan-tao1,2,CHENGJun-sheng1,ZENGMing1,ZHENGJin-de3

(1. State Key Laboratory of Advanced Design and Manufacture for Vehicle Body, Hunan University, Changsha 410082, China;2.Modern Engineering Training Center, Hunan University, Changsha 410082, China;3. School of Mechanical Engineering, Anhui University of Technology, Ma’anshan 243002, China)

Abstract:A novel nonstationary signal analysis method, piecewise polynomial based local characteristic-scale decomposition (PPLCD), was proposed for improving the shortcomings of conventional local characteristic-scale decomposition (LCD), in which the first derivative at extremum points on the connecting line of two extreme value points is discontinuous, thereby the decomposition precision is lowered. Piecewise polynomial was used in PPLCD to replace line connection in LCD, and the interpolation points on the mean curve were computed by the polynomial which was generated according to three adjacent similar extremum points. The theory of PPLCD was studied and then simulation experiments were used to compare the PPLCD with the LCD. The results indicate that the PPLCD is more efficient in improving the orthogonality and veracity of components than the LCD. The proposed method was applied to diagnose the rotor with rub-impact fault successfully which indicates the effectiveness of PPLCD.

Key words:local characteristic-scale decomposition; piecewise polynomial; fault diagnosis; rotor; intrinsic scale component

中图分类号:TH165+.3；TH911.7

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.04.037

通信作者程军圣 男，博士，教授，博士生导师，1968年10月生

收稿日期：2015-01-09修改稿收到日期：2015-03-31

基金项目：国家自然科学基金(51375152；51575168)；湖南省科技计划(2014WK3005)；智能型新能源汽车国家2011协同创新中心；湖南省绿色汽车2011协同创新中心资助项目

第一作者 吴占涛 男，博士，工程师，1982年6月生