基于凸松弛优化算法的相机内外参数标定

柯丰恺　陈幼平　谢经明　张代林

华中科技大学，武汉，430074



基于凸松弛优化算法的相机内外参数标定

柯丰恺陈幼平谢经明张代林

华中科技大学，武汉，430074

摘要：相机内外参数标定的准确性直接影响后期三维重建与真实被测物之间的相似性和三维点云的精度。针对该情况，提出了一种基于凸松弛多项式优化方法来对相机进行标定。该方法通过对优化问题中的高阶单项式进行线性化处理并添加相应的半正定矩阵约束，从而将原非凸优化问题转换为可以快速并准确求解的半正定规划问题，通过求解一次或多次的半正定规化问题来逼近或求解出原优化问题的全局最优解。实验数据证明了该方法的可行性与精确性。对于其他多视角几何中的多项式优化问题，该方法同样存在着良好的通用性与适应性。

关键词：最优化；相机标定；三维重建；半正定规划；全局最优解

0引言

计算机视觉是对人类和动物的视觉的一种模拟，通过对采集到的图像进行处理和分析来获取外界信息。麻省理工学院的Marr[1]将计算机视觉对外界的理解分为基元图、2.5维图以及三维模型三个阶段。因此，三维模型的重建是计算机视觉的关键目标。随着图像处理技术以及成像设备的发展，三维重建已经被广泛应用在摄影测量、虚拟现实、数字娱乐等领域[2]。

相机标定也称相机定标，是三维重建里必不可少的步骤。三维重建的效果与三维坐标点的精度直接取决于相机内外参数的标定精度。相机标定的内外部参数包括焦距、畸变系数、中心点及与世界坐标系之间的旋转矩阵和平移向量等。由于在成像过程中和角点提取过程中不可避免地会加入噪声，因此如何从这些干扰当中正确地估计出相机的几何参数与光学参数就是最优化算法需要解决的问题。Hartley等[3]认为三维重建中最简单的双视图三角化问题对应于一个一元六次方程的求根问题，最多情况下局部最优解可达3个。当为三视图时，对应于一个一元47次方程，故其局部最优值可达24个[4]。因此三维重建过程中的最优化问题大部分具有非线性、非凸性且多模态性(即存在多个局部最优解)等特点，这也是其大部分问题始终没有一个可靠、高效的解决方法的原因。

目前，对于多视角几何下最优化问题的求解算法主要可以分为三大类。第一类是线性求解算法，这类算法主要以奇异值分解为主，该方法将所有的未知量罗列成n×1的列向量x，并从关于这些未知量的等式中提取出对应未知量的系数写成Ax=0的形式，对系数矩阵A进行奇异值分解，即A=UDV，则矩阵V的最后一列即为所求系数[5]。还有一些改进方案，如文献[6-7]中的方法。这类方法求解速度快，但由于没有考虑噪声的性质，因此没有几何上的意义。第二类是通用最优解算法，这类方法通用性较强，并不针对某一类特定问题，不论是线性问题还是非线性问题均可，但优化的最终结果是局部最优解还是全局最优解取决于初始点的选择。这类算法大体分为两种，其中一种较为传统，代表有梯度下降法、牛顿法等，这种通用算法的优点是能较快地收敛到最优解，但很大几率收敛到局部最优解。另外一种是智能算法，这种优化算法的代表有李京[8]提出的遗传粒子群优化算法、李永明[9]提出的人工神经网络反向传播算法以及混沌粒子群优化算法等，其共有的特点是有策略性地、广泛地将初始点或样本分布于优化问题可行域内并设定好优化方向与迭代条件，通过大范围、多方向地对最优解进行求解，因此迭代次数与计算量比梯度下降法等前一种通用最优解算法多得多，计算时间更长，这种算法由于有多个备选最优值，故有更大概率获得全局最优解，但无法保证每次均收敛于全局最优解。第三类是全局最优化算法，这一类被解决的问题很少，如针对L∞范数下的多视角几何最优化问题[10]以及针对仿射相机下的L2范数下的多视角几何最优化问题等[11]。总而言之，最普遍的基于高斯分布的噪声模型下(也即L2范数下)的多视角几何优化问题仍是一个开放性问题。

基于上述问题，本文提出了针对L2范数下的多视角几何全局最优化算法，并利用红蓝的棋盘格标定板来改善标定过程中对角点的提取精度。

1相机模型

如果把普通的二维投影相机成像看作是一个函数映射过程的话，那么这个过程是将空间三维点映射到相机成像面上的平面二维点的过程。它可以表示为

(1)

其中，s是标量，x与X分别是成像面的二维点以及空间的三维点，K包含了相机的内部参数，R和t分别是相机相对世界坐标系的旋转矩阵和平移向量。对相机参数的标定就是对式(1)中的K、R及t的标定。

通常来说，相机标定主要分为两种：一种是自标定，即根据实际生活或工作场景中的已知参照物来对相机进行标定，广泛应用于机器人领域中；另外一种是基于标定物的标定，这种标定方法精度更高，主要采用精确制作的二维或三维的标定物。标定图案有棋盘格的，有圆的及不规则图案的，其中棋盘格标定模板制作因工艺简单且其鞍点辨识度高而得到广泛应用。棋盘格标定板的对比色有很多种，图1a所示为传统的黑白棋盘格标定模板，由于其在强光下存在鞍点模糊的情况，故本文采用红蓝的棋盘格样式来进行标定，如图1b所示。

(a)黑白棋盘格标定模板(b)红蓝棋盘格标定模板图1　标定模板

2多项式优化

为了获取准确的相机内外部参数，需要某种标准来衡量标定质量的好坏，通常使用的就是以相机内外部参数为未知量及空间三维点与平面二维点为已知量的某个累加函数。大量的经验与实验数据表明，数字图像处理中的噪声分布大致符合高斯噪声分布。因此，已知m个对应点，则相机标定的最优化问题可以表示为

(2)

由上述知，标定的参数中含有旋转矩阵R，它存在着RTR=I和det(R)=1的非线性约束，展开则为7个多项式约束条件：

(3)

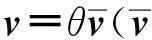
(4)

这种利用向量表达旋转矩阵的方式有效地减少了矩阵参数个数，但由于旋转角θ与π-θ对应于同一旋转矩阵，故在向量v与旋转矩阵R相互转化时，存在映射模糊的问题[12]。

为了避免上述问题，本文直接采用R的矩阵表达形式，并利用Lasserre[13]在2001年提出的凸松弛优化方法来计算相机的内外部参数值。

对于一个标量多项式优化问题，其通用的表达式为

(5)

其中，χ∈Rn,g0(χ)与gi(χ)均为标量的多变量多项式。在Lasserre[13]提出的凸松弛方法中，多项式优化问题的可行域从高维空间变换成无穷维的概率函数空间，每一项不同的高阶单项式被视为关于某一个非负概率函数的矩。在将原问题转化为线性规划问题的同时，根据概率函数空间的特性，添加一个或多个半正定矩阵约束。通过求解一系列呈递进分层式的半正定规划问题，逼近或计算出原多项式优化问题的全局最优解。该凸优化的方法可以归纳为以下步骤：

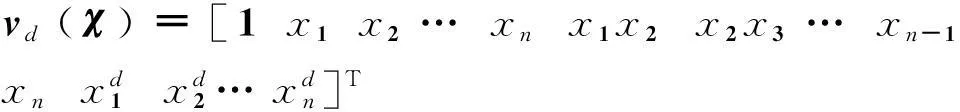
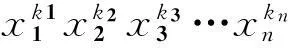
(3)求解前两步中新构成的半正定规划问题，若求得的解不满足事先设定的收敛条件，则将d加1并重复上述步骤。

以Henrion等[14]在其论文中的多项式问题为例:

(6)

分别将式(6)中不同的单项式替换为新的变量，例如将x2替换为y01，对应的新的半正定规划问题为

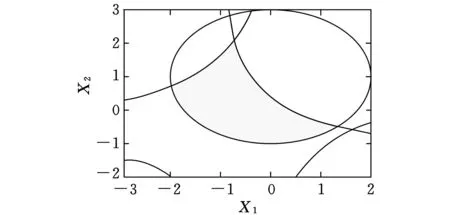
(a)原多项式问题可行域

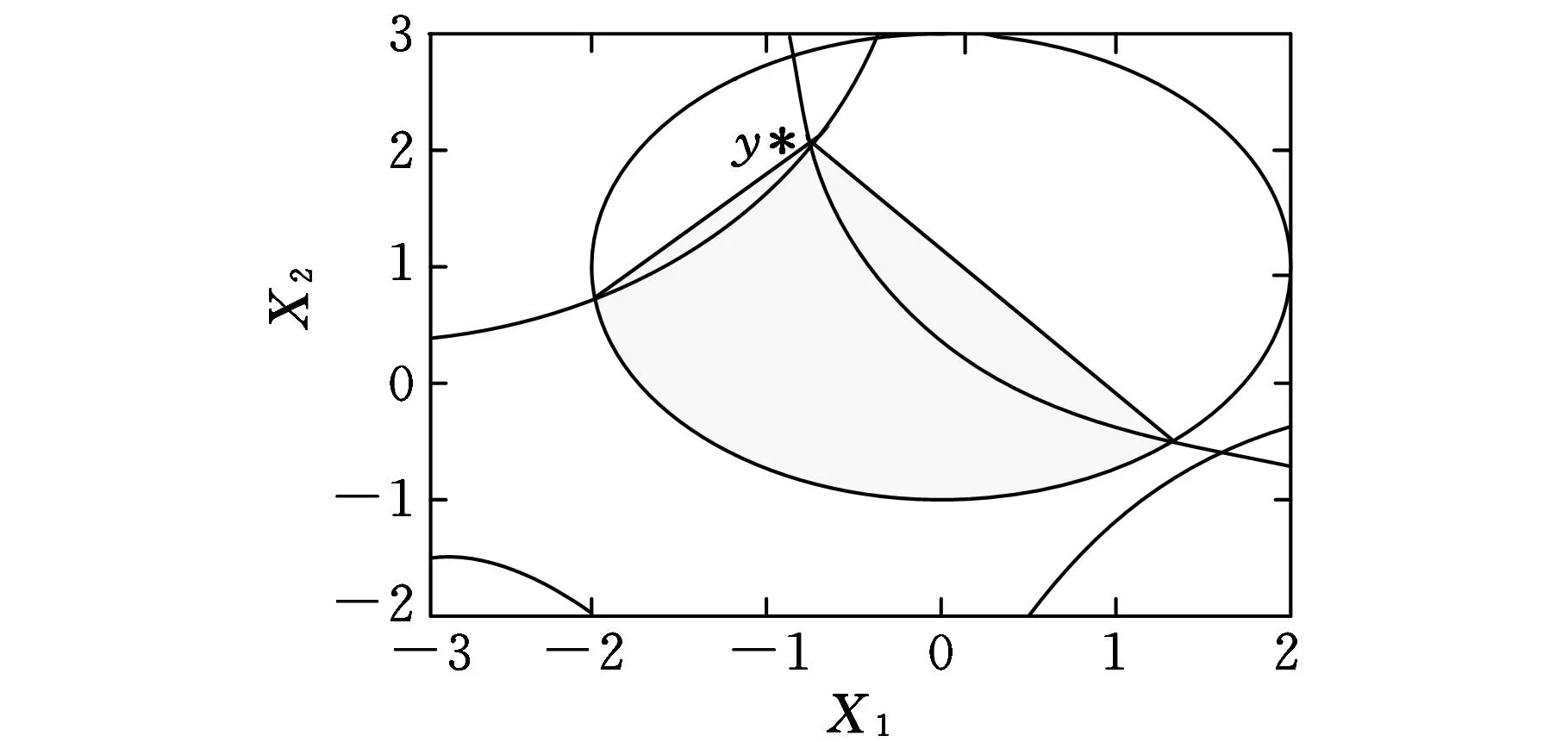
(b)二阶凸松弛可行域

(7)

由图2b所示，经过凸松弛后的半正定规划问题，很好地逼近了原多项式问题。由于求解半正定规划问题的全局最优解已非常成熟，利用现有的开源程序Sedumi可以对半正定规划问题式(7)进行快速求解，所求得的全局最优解也即原多项式问题的全局最优解[15]。

3实验结果与分析

(a)红蓝标定板效果图(b)黑白标定板效果图图3　效果图

图4　角点检测示意图

(8)

(9)

(a)牛顿优化算法

(b)凸松弛优化算法图5　标定误差总体分布图

由图5与实验数据所知，经凸松弛优化处理后，角点的估计误差明显减小，且相机参数估计误差更小。

为了定量分析经过牛顿优化算法和经过凸松弛优化算法后的参数精度与准确度，本文采用两种算法对双目相机进行标定，通过双目相机来进行空间尺寸测量，依据测量出的数据精度来判断各自标定效果的好坏。

如图6所示，本文对棋盘格标定板的方块尺寸以及游标卡尺的尺寸进行测量，图中标记点为测量目标尺寸。经过双目视觉三角化求得角点空间坐标后，计算的尺寸长度如表1与表2所示。由表中数据可知，凸松弛在测量棋盘格方格和游标卡尺刻度值时的平均误差均远小于牛顿法所测量的结果，这证明了本文提出的凸松弛优化方法在摄像机标定过程中的有效性与正确性。

(a)棋盘格(b)游标卡尺图6　测量样本图

实验次数凸松弛法测量尺寸(mm)牛顿法测量尺寸(mm)真实尺寸(mm)凸松弛法平均误差(%)牛顿法平均误差(%)125.107523.1102225.366829.2489324.548226.0156425.172424.9117525.063826.0006624.738524.8262724.913327.0856825.068526.9726925.715724.71301025.553926.9841250.53.95

表2　游标卡尺刻度测量数据

4结论

由于相机成像与角点检测过程中不可避免地会引入噪声干扰，因此相机标定优化问题中存在着多个局部最优解。本文提出了一种基于L2范数的全局最优算法。该算法通过求解一系列的半正定规划问题来逼近与求得目标函数的全局最优值。实验结果表明，与传统优化方法相比，该凸松弛的方法能快速有效地逼近全局最优解，相机标定参数的误差得到大幅减小。

参考文献：

[1]MarrD.Vision:aComputationalInvestigationintotheHumanRepresentationandProcessingofVisualInformation[M].NewYork:W.H.FreemanandCompany, 1982.

[2]HartleyR,ZissermanA.MultipleViewGeometryinComputerVision[M]. 2nded..England:CambridgeUniversityPress, 2004.

[3]HartleyR,SturmP.Triangulation[J].ComputerVisionandImageUnderstanding,1997, 68(2):164-157.

[4]SteweniusH,SchaffalitzkyF,NisterD.HowHardis3-viewTriangulationReally?[C]//ProceedingsofIEEEInternationalConferenceonComputerVision(ICCV).Beijing:2005:686-693.

[5]Bookstein F. Fitting Conic Sections to Scattered Data[J]. Computer Graphics and Image Processing, 1979, 9: 56-71.

[6]Chesi G, Garullli A, Vicino A, et al. Estimation the Fundamental Matrix Via Constrained Least Squares: a Convex Approach[J]. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2002, 24(3): 397-401.

[7]Hartley R. Indefense of the Eight-point Algorithm[J]. IEEE Trans. on Pattern Analysis and Machine Intelligence, 1997, 19(6): 580-593.

[8]李京. 基于遗传粒子群优化算法的遥感图像分类方法研究与应用[D]. 北京：首都师范大学，2013.

[9]李永明. 人工神经网络BP学习算法的研究及在人脸识别中的应用[D]. 济南：山东大学，2012.

[10]Kahl F, Hartley R. Multiple View Geometry under the Norm[J].Pattern Analysis and Machine Intelligence, 2008,30(9):1603-1617.

[11]Tomasi C, Kanade T. Shape and Motion from Image Streams under Orthography: a Factorization Method[J]. Int. Journal of Computer Vision, 1992, 9(2): 137-154.

[12]Richard H, Jochen T, Dai Yuchao, et al. Rotation Averaging[J]. International Journal of Computer Vision, 2013,103(3):267-305.

[13]Lasserre J B. Global optimization with Polynomials and the Problem of Moments[J]. SIAM J. Optimization, 2001, 11(3): 796-817.

[14]Henrion D, Lasserre J B. Solving Nonconvex Optimization Problems-How Gloptipoly is Applied to Problems in Robust and Non-linear Control[J]. IEEE Control Systems Magazine,2004,24(3): 72-83.

[15]Sturm J F. Using SeDuMi 1.02: a Matlab Toolbox for Optimization Over Symmetric Cones[J]. Optimization Methods and Software, 1999,11(12):625-653.

[16]Waki H, Kim S, Kojima M, et al. Sparse POP: A Sparse Semidefinite Programming Relaxation of Polynomial Optimization Problems[J]. ACM Transactions on Mathmatical Software, 2008，35(2)：1-15.

(编辑袁兴玲)

Internal and External Parameter Calibrations of a Camera Based on Convex Relaxation Optimization Algorithm

Ke FengkaiChen YoupingXie JingmingZhang Dailin

Huazhong University of Science and Technology,Wuhan,430074

Abstract:The similarity between the real object and the reconstructed model and the precision of the 3D point cloud were determined by the accuracy of the internal and external parameters of the camera. A convex relaxation algorithm was proposed to deal with the problems of camera calibration. Each monomial in the polynomial optimization problem was replaced by its corresponding linear item and some semi-definite matrix inequalities were added. The global optima could be approximated or achieved by solving one or more semi-definite programming problems. The experimental results confirm the feasibility and the accuracy of this algorithm. Moreover, the algorithm can be applied to the problems of camera calibration and some other polynomial optimization problems in multiple view geometry.

Key words:optimization; camera calibration; 3D reconstruction; semi-definite programming; global optimum

作者简介：柯丰恺，男，1989年生。华中科技大学机械科学与工程学院博士研究生。主要研究方向为最优化算法及三维重建。陈幼平，男，1957年生。华中科技大学机械科学与工程学院教授、博士研究生导师。谢经明，男，1966年生。华中科技大学机械科学与工程学院副教授。张代林，男，华中科技大学机械科学与工程学院讲师。

中图分类号：TP751.1

DOI：10.3969/j.issn.1004-132X.2016.05.011

基金项目：国家自然科学基金资助项目(51174151)

收稿日期：2015-05-13