考虑装配误差的车门关闭力计算

宋　凯　刘九五　成艾国

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082



考虑装配误差的车门关闭力计算

宋凯刘九五成艾国

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

摘要：针对由装配误差引起的车门关闭力预测不准确问题，提出了一种计算精确车门关闭力的方法。该方法首先建立车门关闭过程中各部件相应的力学模型，在影响关闭力大小的几个因素中以门锁为例，通过蒙特卡罗模拟得到车门装配过程中门锁位置误差的概率分布统计，然后在计算关闭力的数学模型中结合门锁位置装配误差，得到车门关闭力的概率分布结果，最后对样车进行关闭力测试，试验结果表明考虑装配误差的车门关闭力的计算精度明显提高。

关键词：关闭力；装配误差；蒙特卡罗模拟；力学模型

0引言

如今的消费者对汽车乘坐的舒适性要求越来越高，所以汽车制造厂也在寻求提高汽车舒适性并且能符合国家标准的方法。根据JDPOWER的市场调查，开关门力大始终是顾客抱怨最多的质量问题之一[1]。车门关闭力也就是关紧车门需要的最小能量，对于现在的汽车品牌形象是非常重要的，我们常常把车门关闭的舒适性看作汽车制造厂制造水平的一种表征。而车门关闭力的预估一直是国内汽车厂商的弱项，如果能在设计制造前期估算出有效的关闭力大小，这对于改进车身结构、提高乘车舒适性有较大的帮助。

近几年国内外学者在车门关闭力方面进行了许多有效的研究工作。文献[1-2]通过ADAMS建立车门系统仿真模型来模拟计算车门关闭速度以及车门系统与车门关闭力变化的相互关系；Qiu等[3]用有限元模型来模拟计算车门关闭速度；文献[4-5]通过建立车门各部件关门过程中消耗能量的数学模型来求得车门的关闭力大小，其计算结果具有一定的精确度。

以往的研究中主要将车门系统(包括车门内外板及附件，其中附件有铰链、密封条、门锁等)视为理想模型，并没有将车门系统的制造装配误差这一影响因素考虑在内，所得的车门关闭力大小与试验数据有一定偏差。蒙特卡罗模拟方法是通过大量的随机样本实验归纳出统计结果的一种概率统计分析方法，通过抽样理论近似求解数学、物理及工学问题。本文利用蒙特卡罗模拟得到较精确的车门系统装配误差估算值，并将装配误差值代入计算关闭力的数学模型中，得到车门关闭力大小结果。将该方法计算得出的结果与试验结果进行比较，证明了该方法的有效性。

1车门关闭力的计算模型

1.1车门关闭过程耗能情况分析

车门关闭力定义为使车门从最大开启位置到达车门锁锁紧位置需要的能量。从车身其他部件都处于静止状态开始，将门打开至最大位置，然后给车门一个推力，使车门能克服限位器的阻力，绕铰链轴开始转动，最后车门锁与车身锁扣锁紧，车门贴紧B柱，运动结束。车门系统的每个部件都有能量消耗，我们需要模拟计算出不同部件所消耗的能量，再将所得到的各个部件所消耗能量的和作为车门关闭所需的能量。

在车门关闭的过程中，靠铰链支持车门关闭时车门的重量，铰链始终是在克服摩擦力做功，所以可以通过计算摩擦力得到铰链消耗的能量。当车门锁门闩与锁扣开始接触时，车门锁就对车门有反作用力，车门锁所消耗的能量主要包括门闩的扭矩以及锁扣摩擦耗能与门锁完全扣上里面的弹簧需要消耗的能量。在门锁开始做功的同时，车门四周的密封条开始压缩，我们可以根据密封条的受压变形特性(CLD)曲线以及它的压缩量来计算得到密封条消耗的能量。最后，随着车门的关闭，一部分空气被压缩进车舱，这部分空气由于迅速压缩，也会对车门会产生一个阻力，我们称之为空气阻力。

所以影响车门关闭好坏的因素有很多，包括密封条和门锁的阻力、空气阻力以及车门的惯性等。其中影响最大的是密封条的阻力以及空气阻力。在关门过程中，限位器虽然在开始有一定的阻力，但整个过程中它的正功和负功可以抵消，基本不做功。

为了预估车门关闭所需要的最低能量，车身的几何以及物理参数应该测量精确，预估的最低关门能量也是评价车门关闭好坏的标准之一。

1.2车门关闭过程的耗能模型构建

车门关闭过程主要有五部分耗能，分别是门重耗能、铰链耗能、密封条耗能、门锁耗能、空气阻力耗能。

1.2.1门重耗能模型

能量消耗首先考虑铰链以及车门的重量。门重以及铰链轴会通过势能来影响能量的消耗，通常来讲铰链轴不是精确垂直的，这样门重就会绕铰链轴产生一个转矩Tw，使车门能在重力的作用下自动关闭，车门打开时受力情况如图1所示。

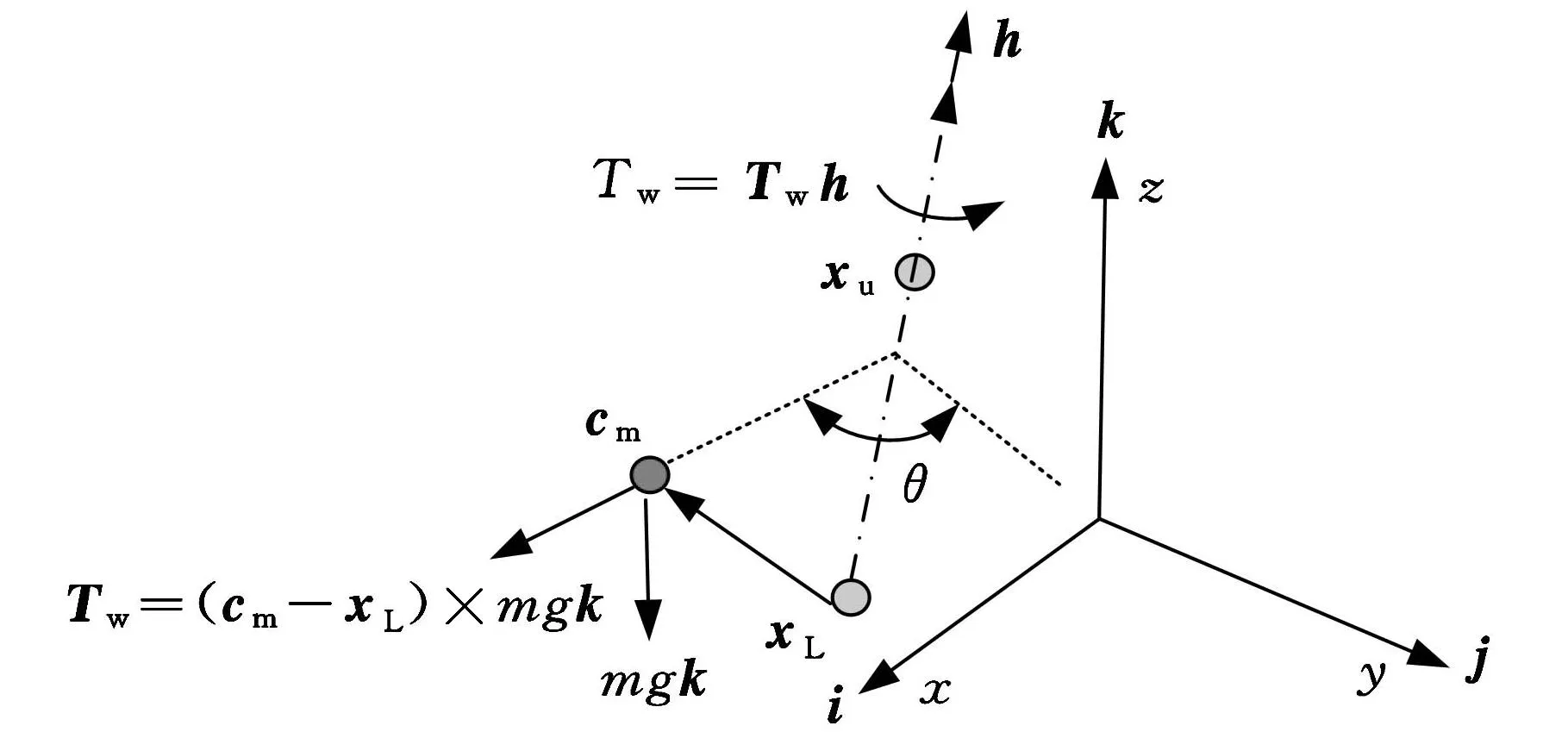
图1　车门受重力影响情况

铰链轴与垂直面的角度会直接影响车门开启时重心是会上升还是下降，角度的变化会引起车门势能的变化。我们设计的目的就是为了更好地利用势能，让车门能利用自己的势能来帮助使门关闭。车门重力使车门关闭的转矩如下:

Tw=[(cm-xL)×(mgk)]h

式中，cm为车门质心坐标；xL为下铰链质心坐标；m为门的质量；h为铰链轴的单位向量；k为z向单位向量。

通过坐标变换，车门的势能可以用下面方程来表示：

Ew=mg(cmm-cmo)k

(1)

式中，cmm为门最大开启位置时重心的坐标；cmo为车门关闭时重心的坐标。

1.2.2铰链耗能模型

其次考虑车门由于铰链系统摩擦所消耗的能量。铰链系统通过一根铰链轴将两个铰链连接起来，使车门能够绕铰链转动，车门有上下两组铰链，铰链结构如图2所示。

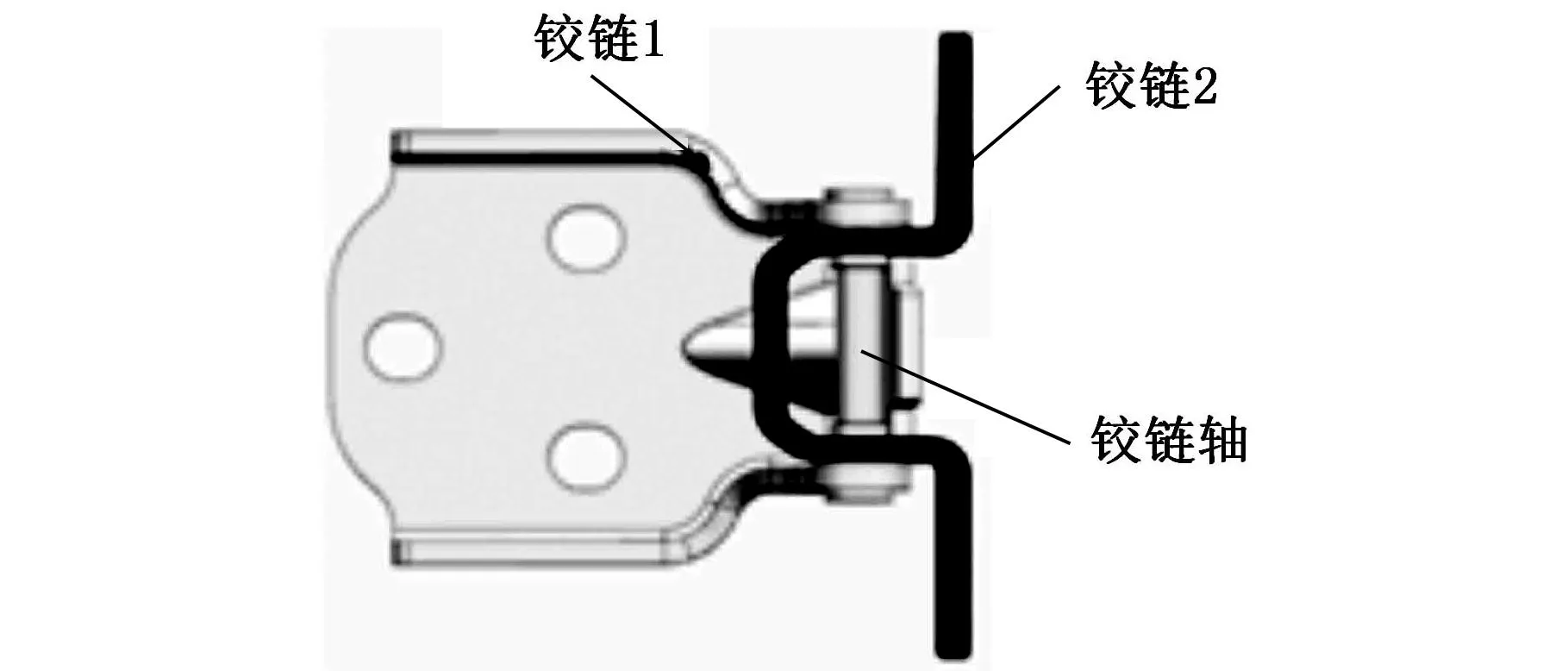
图2　铰链结构

在关门的过程中铰链轴与铰链的摩擦会形成阻碍关门的力，从而消耗关门能量，摩擦力分两部分，一部分是车门重力使铰链1与铰链2产生摩擦力，还有一部分就是重力矩使铰链与铰链轴产生摩擦力。铰链的受力情况如图3所示。

图3　车门铰链受力情况

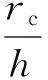
(2)

式中，μh为摩擦因数；rh为铰链轴的半径；h为两铰链的距离。

铰链耗能中由摩擦力消耗的能量方程如下：

Eh=ThingeΔθ

(3)

式中，Δθ为门关闭运动的角度。

1.2.3密封条耗能模型

第三个能量消耗因素是车门密封条的压缩变形。密封条由两部分组成，一部分是泡体，材料为海绵橡胶，主要起到密封作用，在泡体上每隔一段距离会有一个排气孔，防止车门和侧围间出现气垫现象；另一部分是U形实心体，材料为密实橡胶，具有几乎不可压缩的材料特性，橡胶内部含有钢丝织带的骨架，主要作用是将密封条较好地固定在车门框上。它所消耗的能量与它的材料密度和海绵橡胶的特殊性能有关。

在车门关闭将密封条压缩的过程中，车门是绕铰链旋转的，靠铰链侧的密封条会先进行压缩，为方便计算将密封条分为n段，假定相同段的密封条压缩量一样，分别计算不同段消耗的能量。密封条消耗能量分两部分计算，一部分为海绵材料的压缩变形做功，一部分为排气孔排气时产生的阻尼力做功。为了简化整个密封条的模型，将整个密封条的能量消耗用几个弹簧元件来模拟，用密封条的CLD曲线来定义弹簧元件的特性[6]。密封条的CLD曲线与密封条的截面和材料特性有关，如泊松比、密度等。简化后的密封条模型如图4所示。

图4　简化的密封条

每个单元的变形可以用胡克定律来表示：

fi=kiuii=1,2,…,n

式中，fi为胡克力；ki为密封条的弹性因素；ui为每段密封条变形量。

整个密封条被分为n等份后，消耗力计算矩阵如下：

不同段的密封条变形量为

ui=2Risin(α/2)

(4)

式中，Ri为车门的转动半径;α为每段密封条从开始压缩到运动结束车门所转过的角度。

n段密封条海绵材料压缩能量消耗如下：

(5)

密封条排气孔排气时根据质量守恒定律和动量定理,可以得到：

通过整理计算可得

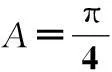
式中，ρa为空气密度；l为排气孔距离；V为长l段密封条里的空气体积；ve为密封条内空气流动速度；Fl为长l段密封条内的排气孔阻力；ml为长l段密封条里的空气质量；w为密封条截面宽度；hs为密封条截面高度；A为排气孔面积；D为排气孔半径。

排气孔阻力做功为

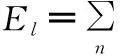
(6)

密封条做的总功为

Em=Ek+El

(7)

1.2.4门锁耗能模型

第四个能量消耗为门锁机构的运动，本文只考虑门锁机构在车门关闭时消耗的能量。门锁的运动就是指锁扣卡进锁闩的过程，在这个过程中锁扣会受到棘爪和弹簧的阻力。由于锁扣和棘爪在运动的过程中有面接触，故会产生摩擦力消耗能量。锁扣旋转运动的最后它会停在缓冲的橡胶块上，由于橡胶块有一点变形，故也会储存一部分的能量。门锁机构如图5所示。

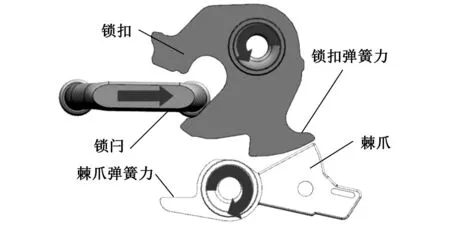
图5　门锁基本结构

根据Udriste[7],门锁机构的运动可以转化到一个平面上，因此可以将门锁结构近似为一个平面机构来研究。

门锁消耗的能量可以分成两部分，一部分是锁闩的弹簧变形消耗，另一部分是棘爪弹簧力及棘爪与锁扣的摩擦力消耗：

Esk=E1+E2

(8)

式中，Es为锁扣弹簧的弹性模量；Fs为锁扣弹簧力；rl为锁扣的旋转半径；θ为锁扣的转动角度；k2为棘爪弹簧的弹性系数；x2为棘爪弹簧变形量；μs为棘爪和锁扣的摩擦因数。

1.2.5空气阻力耗能模型

第五部分能量消耗是空气阻力消耗，空气阻力耗能是指在车门关闭过程中将一部分的空气压缩进车身的密闭空间内，压缩进车厢的空气比排气孔排出的空气多，车内的压力增大，在关闭瞬间空气对车门就会产生压力，为了预测这个关闭力的大小，我们假定车内空间为一个简化的理想模型，该模型主要是模拟前车门关闭时的情形，如图6所示。

图6　空气阻力理想模型

根据理想气体状态方程可得气体泄漏速度为

式中，p为舱内气体压力；pa为大气压力；vE为气体泄漏速度。

车门压入的空气会从AE流出一部分，由空气质量守恒可以推出：

式中，V为车内空气体积；AE为泄气孔面积；ρ为气体密度。

空气阻力对车门的力矩可用如下方程表示：

(9)

式中，Am为门洞面积；r为车门上的点到铰链中心轴的距离；Δθm为从车门密封条与侧围密封条接触到车门完全关闭所转过的角度。

综合上述各部件消耗的能量公式(式(1)、式(3)、式(7)～式(9))，可以得出车门关闭所需的总能量为

E=Ew+Esk+Eh+Em+Ef

(10)

2基于蒙特卡罗的车门装配误差模拟

在车门装配过程中，由于制造误差以及装配误差会使装配后车门的位置与理想状态的位置有偏差，按理想状态计算出来的车门关闭力会与实际情况有一定误差，所以为了更加精确预估车门关闭所需要的能量，本文运用蒙特卡罗模型模拟车门装配误差，结合车门铰链与锁的装配位置误差以及其他各部件的参数，来计算得到有效的车门关闭力。

门的附件包括铰链系统和门锁系统，铰链系统包括上铰链和下铰链，控制门的3个方向自由度(x,y,z),门锁系统通过门闩和锁扣控制门的y向和z向的自由度，如图7所示。本文将铰链及其他制造误差定义为标准值，只考虑门锁的装配误差，通过单独研究门锁装配误差对关闭力的影响，来验证本文方法的可行性。

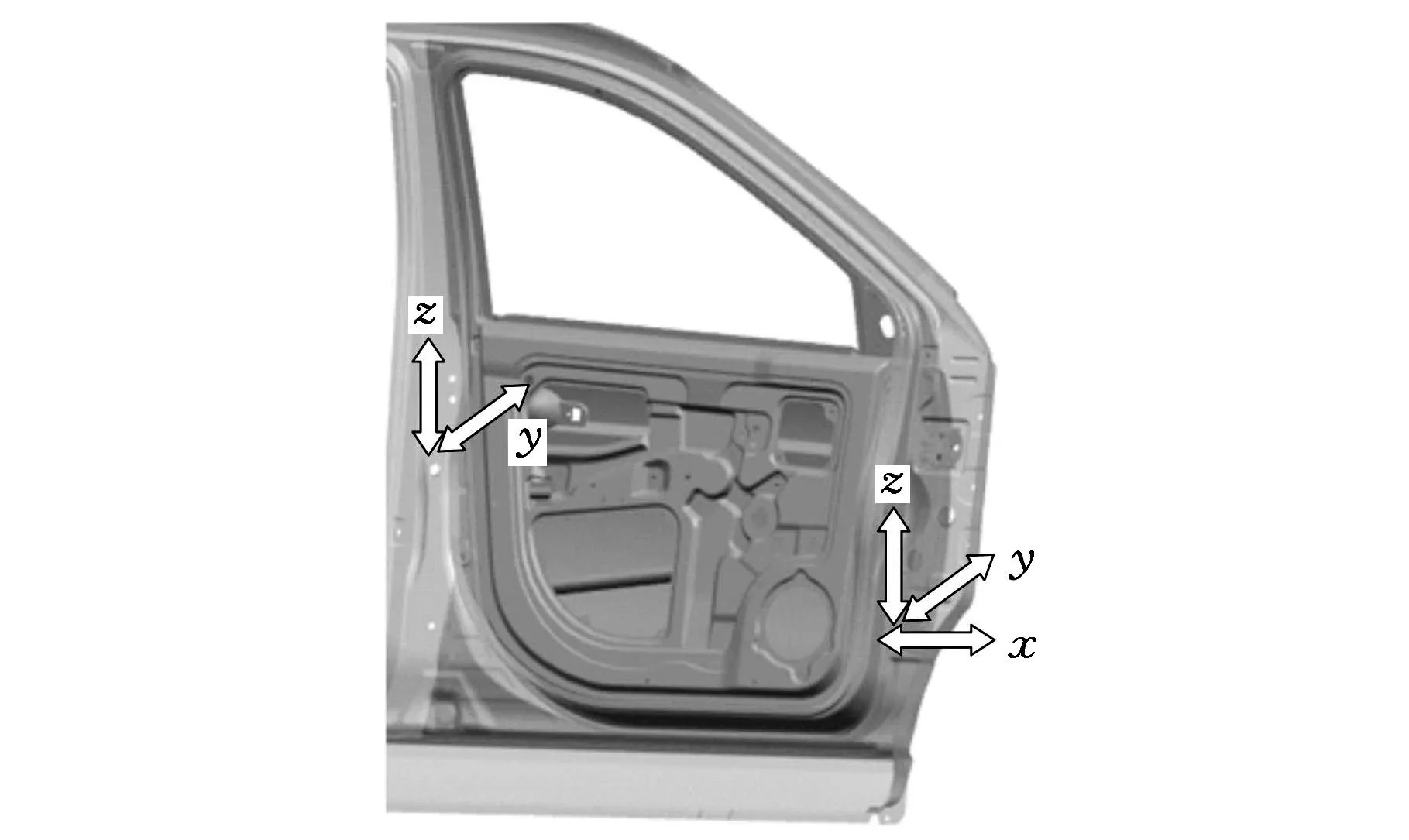
图7　车门附件的位置变化方向

通过输入零件的制造公差数据，对车门装配进行蒙特卡罗仿真模型模拟，可以得到门锁装配误差的范围。锁和锁扣位置的变化直接影响车门关闭力，它们一个很小的误差就会引起关闭力的变化。

蒙特卡罗仿真(MCS)通过建立与问题相似的概率模型，对模型进行大量而简单的重复抽样随机模拟，利用所得到的结果求出特征的统计估计值，并对估计值的精度作出评估[8]。

蒙特卡罗仿真的过程为：首先确定每个偏差源的概率分布，再依据计算精度要求确定抽样次数，采用随机数发生器对源偏差随机采样，每采样一次进行一次偏差分析，得到一个装配偏差样本，当样本数达到抽样次数要求时，即可确定装配偏差的统计参数，如均值、方差等。

在进行蒙特卡罗模拟之前，先从正常生产的车辆中收集100辆车的锁和锁扣位置测量数据，随后统计的位置数据被处理输入到蒙特卡罗模拟中，蒙特卡罗模拟会根据测量的数据生成门锁和锁扣y、z位置的一系列随机值。模拟的次数由计算精度要求确定。

蒙特卡罗模拟法的精度与样本数n有关，在随机变量一定的情况下，增加样本数能够有效地提高计算精度，计算精度与样本数的平方根成正比。根据文献[9]，若模拟结果Fi服从正态分布(μi,σi2)，μi为均值，σi2与si2分别为方差真值与样本方差，那么方差真值的100%(1-α)=95%(α为置信水平)置信区间为

(11)

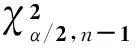
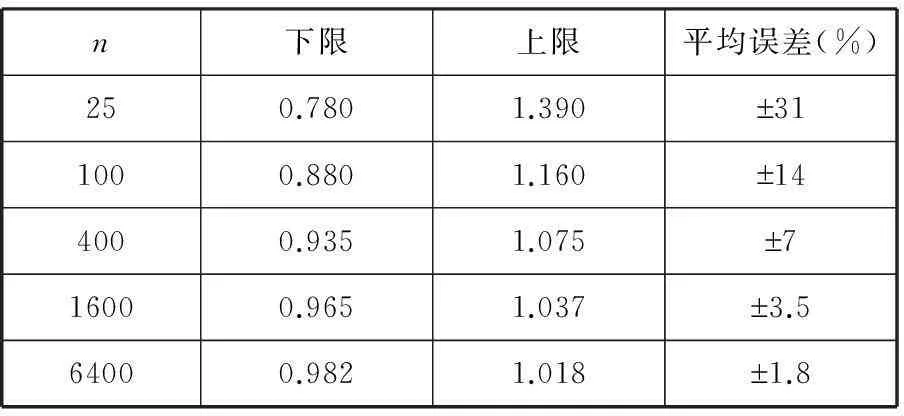
表1　3σi的置信度区间

根据表1并结合此次模拟计算的精度要求，确定模拟次数为6000。

蒙特卡罗模拟生成的门锁和锁扣的一系列位置数据会被输入到关闭力的计算模型并通过计算最后得出关门力的概率分布结果。最后，将计算出来的车门关闭力与在实验室测量的50辆车的数据相比较。

3模拟与试验结果对比

在计算前，需要车门系统的基础数据。表2所示为试验车型密封条的规格。其中包括了门重和它绕铰链轴线的转动惯量。

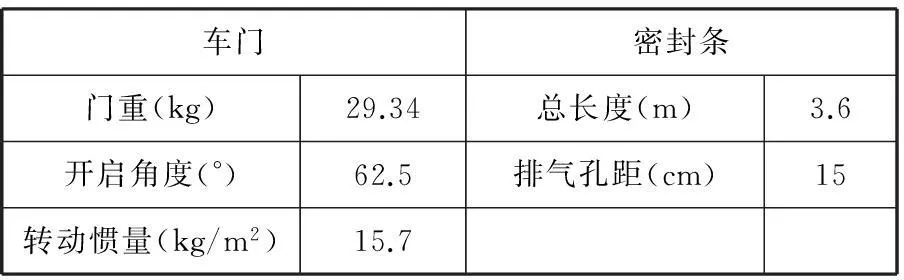
表2　车门及密封条参数

由于整根密封条的材料特性是一样的，故可通过对一段密封条进行压缩试验，得到密封条的CLD曲线。图8所示为该车型密封条CLD曲线。

图8　密封条CLD曲线

3.1车门关闭力模拟计算结果

在不考虑车门装配误差的情况下，将各个参数直接代入关闭力计算的模型中，在计算过程中，将关闭能量转化为关闭力矩大小，力矩半径为车门把手位置到铰链中心轴的距离，力矩的大小能直观地显示关门作用力。

车门在关闭过程中门重一直做功，计算结果为-2.27 N·m。铰链系统整个过程都有耗能，计算结果为0.86 N·m。将该车型的密封条分为24段，在开始关闭过程中密封条没有接触，到最后车门关闭至21°时才开始接触做功，密封条和密封条排气孔共同做功，计算结果为1.93 N·m。门锁在接触后做功，结果为0.45 N·m。在密封条接触后空气阻力做功结果为2.2 N·m，最后计算得整个过程耗能为3.15 N·m。

本文用蒙特卡罗方法模拟门锁的y和z坐标的变化，因为在门锁锁紧的过程中，锁扣沿x轴方向是不受力的，所以门锁x方向的变化对关闭力几乎没有影响。

图9所示是门锁在y轴方向上的装配误差的分布范围， y轴方向很小的位置误差就会影响车门最后关紧的位置，关紧位置沿y轴方向的变化会使车门与侧围的间隙有误差，这样会使密封条最后的受压变形量变大或变小，使得车门关闭力的大小发生变化。在6000次的模拟中，y轴方向的位置误差平均值为-0.6151 mm，标准差为0.343。

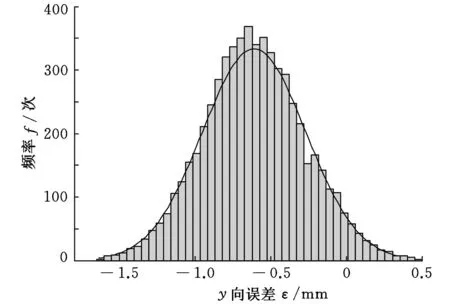
图9　门锁装配y向误差蒙特卡罗模拟概率分布

图10所示是门锁在z轴方向上的装配误差的分布范围，门锁在z轴方向的误差会使车门关紧时的质心位置与定义值发生变化，这就会使由门重消耗的能量发生变化，并且z轴方向的误差会使门锁在扣合过程中摩擦力变化，导致最后的关闭力大小变化。在6000次的模拟中，z轴方向的位置误差平均值为0.165 mm，标准差为0.475。

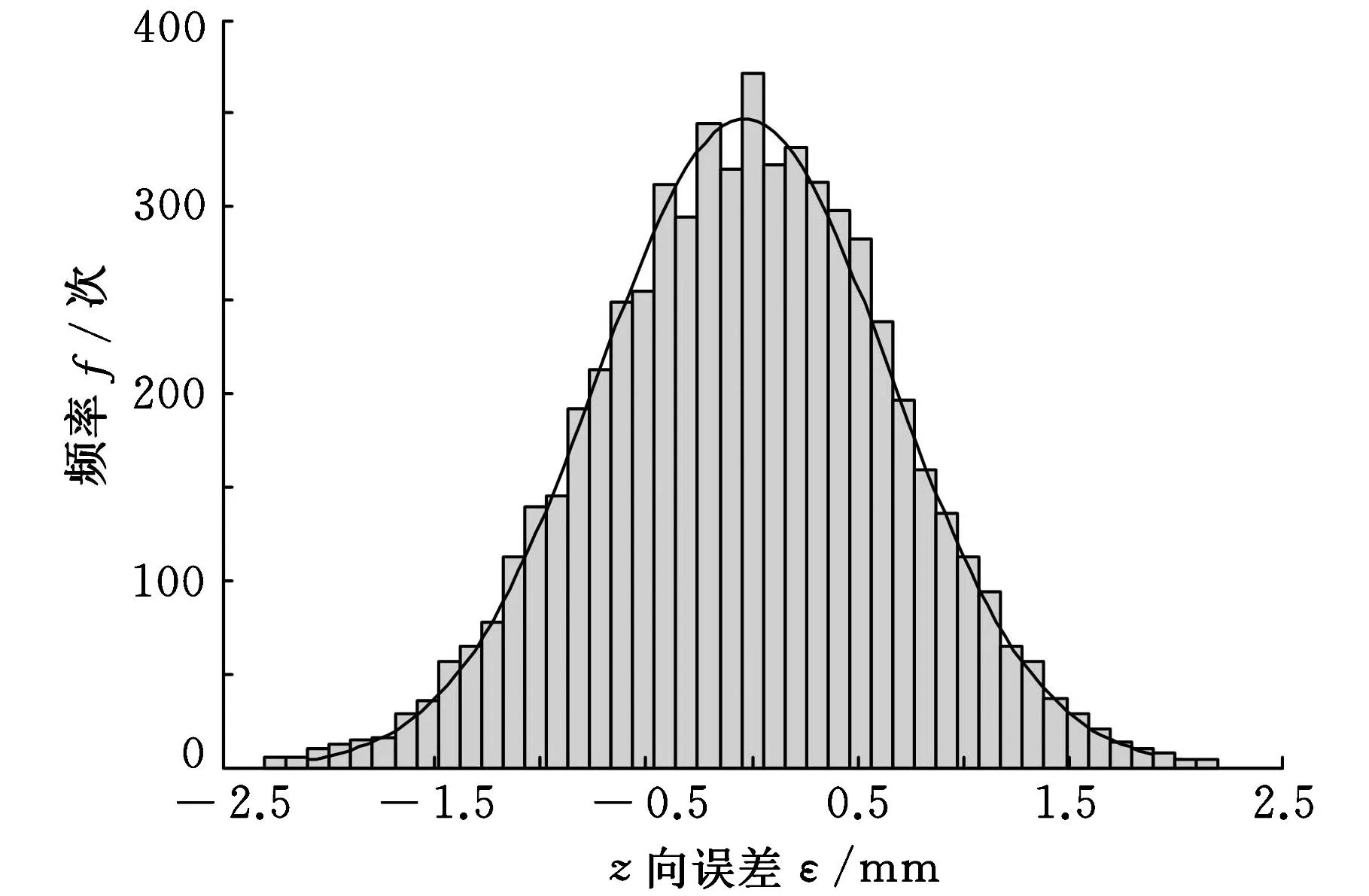
图10　门锁装配z向误差蒙特卡罗模拟概率分布

将以上两个直方图的数据输入到车门关闭力的计算模型中，计算出6000次不同误差下车门关闭力矩的大小，结果如图11所示，关闭力矩的大小范围在2.5 N·m和4.3 N·m之间，平均值是3.361 N·m，标准差是0.268。

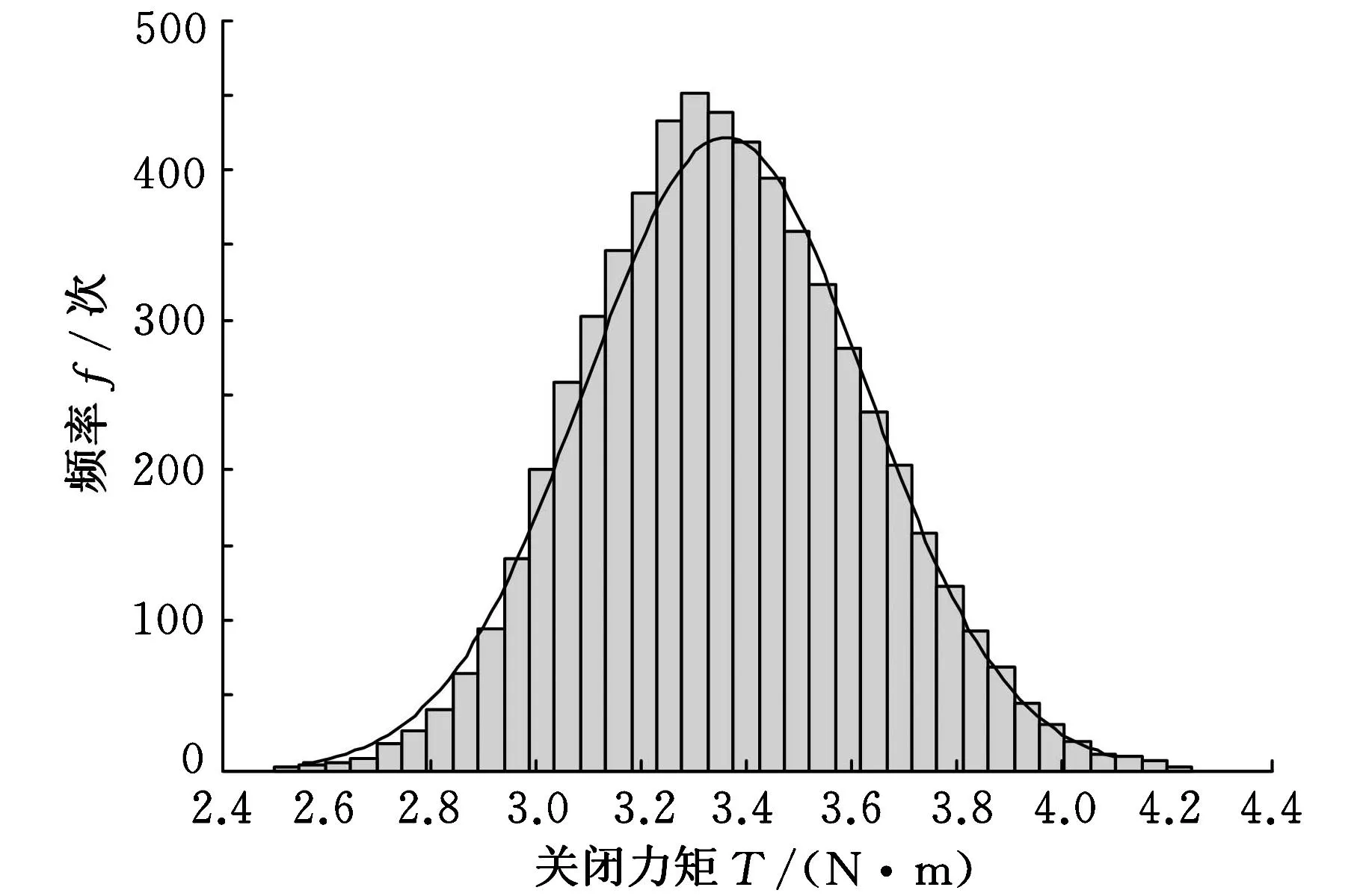
图11　考虑装配误差的关闭力矩计算结果概率分布

3.2车门关闭力试验结果

试验结果来自实验室的50辆汽车在相同环境下的测试。门关闭力的试验是在车门开启的最大位置，通过加能装置在车门把手位置施加一个力，能够让车门刚好锁住，通过力和位移传感器读取试验数据。图12为关闭力试验图。

图12　关门能量测试图

试验数据是通过测试50辆车的左右车门关闭统计的，图13是测量的左前车门关闭力矩的分布图，大小在3.2 N·m到3.9 N·m之间，平均值为3.518 N·m，标准差是0.167。

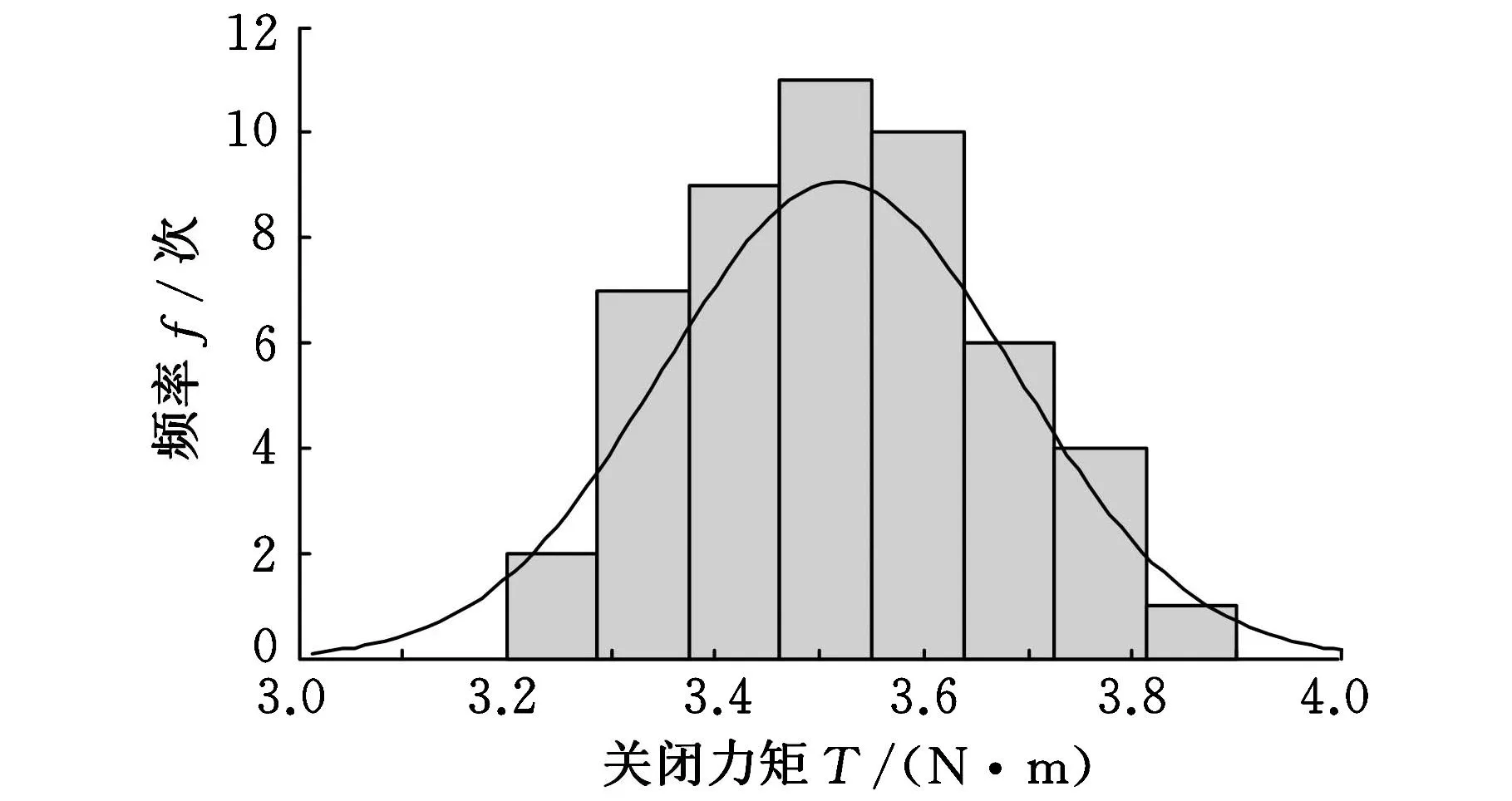
图13　左车门关闭力矩试验结果概率分布

图14所示为右前车门关闭力矩大小的分布图，范围在3.1 N·m到3.9 N·m之间，平均值为3.508 N·m，标准差是0.183。表3所示为计算结果与试验结果的对比。

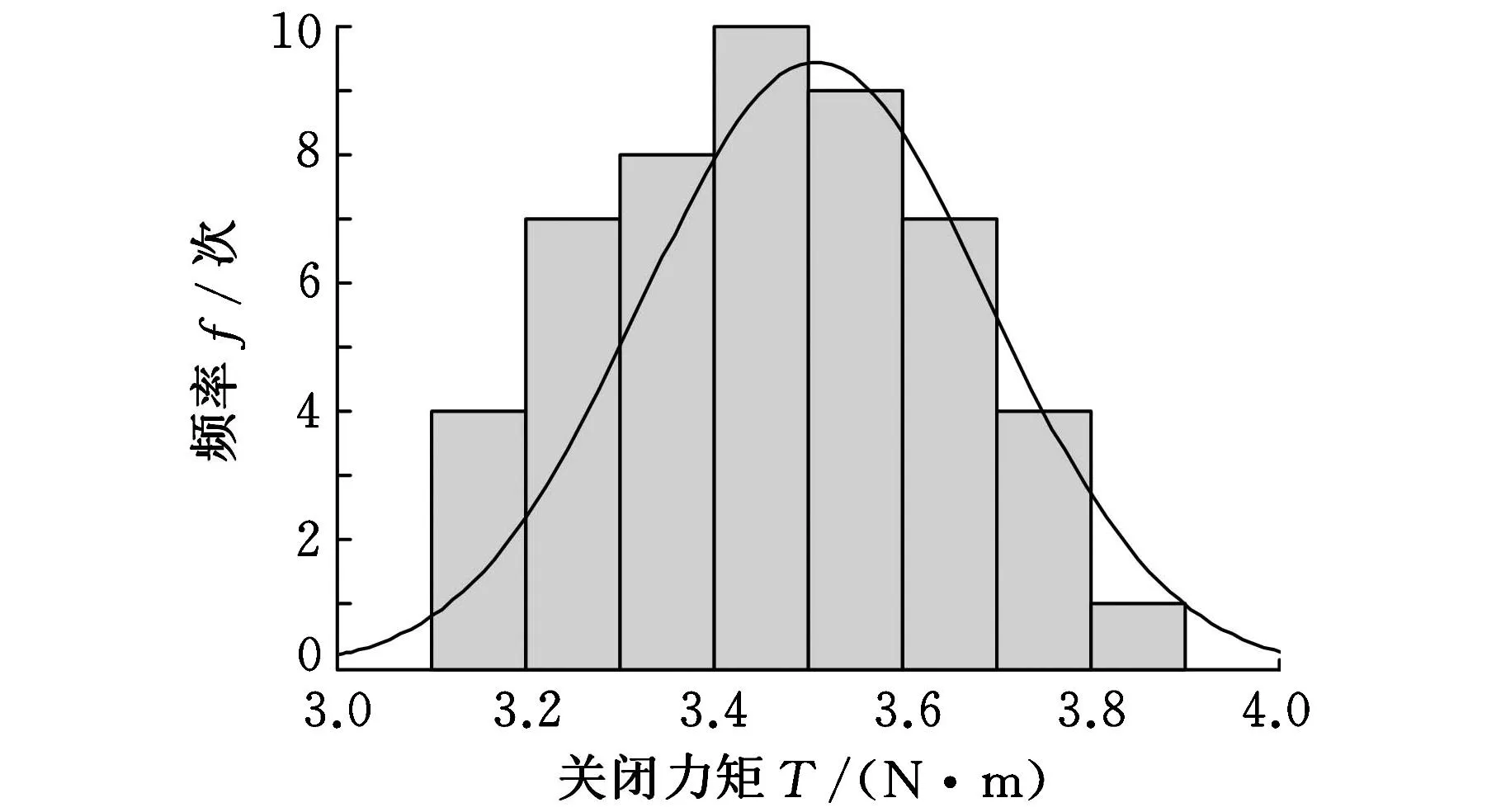
图14　右前车门关闭力矩试验结果概率分布

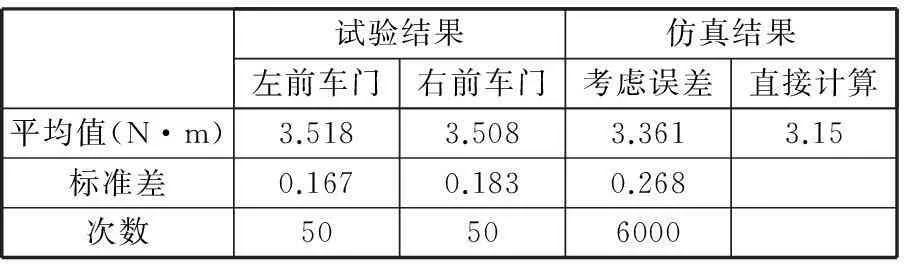
试验结果仿真结果左前车门右前车门考虑误差直接计算平均值(N·m)3.5183.5083.3613.15标准差0.1670.1830.268次数50506000

从上述结果可以看出，考虑了装配误差模拟的关闭力矩计算的平均值跟试验结果相差不到5%，结果比较接近。标准差与试验结果相差较大，这主要是由于试验数据数量与模拟数据数量差距较大的缘故。而不考虑误差直接计算出的关闭力结果与试验结果相差超过10%。

4结论

(1)蒙特卡罗模拟的运用，成功地将车门装配误差结合到关闭力的计算模型中，得到车门关闭力的概率统计分布，并使得关闭力的模拟计算结果与试验数据较接近。

(2)对比考虑装配误差的计算模型结果和直接计算结果，验证了考虑装配误差的车门关闭力预测结果更加接近试验结果，这样的关闭力预测模型能提高预测精度，使设计者能通过该模型很好地预测车门关闭力的大小。

(3)在这个关闭力计算过程中也有很多的部件误差没有考虑，如门内板与侧围匹配面的误差、密封条的时效、门锁弹簧的偏差等。但就结合门锁的装配误差来预测车门关闭力可以看出，部件的误差会对关闭力的计算有一定影响，并且通过本文的方法能够有效地模拟部件误差对关闭力的影响。

综上所述，利用本文提出的分析方法可以研究在车门装配误差影响下的关闭力计算，在设计初期估算出有效的关闭力大小。

参考文献：

[1]Nayak R,Im K．Optimizationof the Side Swing Door Closing Effort[J].SAE Technical Paper,2003-01-0871.

[2]杨蕾，张淑敏，李应军．面向最优关门能量的轿车车门设计[J]．机械制造，2006，44(3):40-42.

Yang Lei，Zhang Shumin，Li Yingjun．Design of Automotive Door Oriented Forward the Optimization of Door Closing Energy[J]．Machinery，2006，44(3):40-42.

[3]Qiu P, Qu Y, Wu S，et al. Finite Element Analysis of Door Closing Effort[J]. SAE Paper,2013-01-1398.

[4]Li J, Mourelatos Z, Schwarze F,et al.Prediction of Automotive Side Swing Door Closing Effort[J].SAE Int. J. Passeng. Cars-Mech. Syst., 2009,2(1):271-284.

[5]尹忠，唐荣平，裘芝敏，等．汽车车门关闭力的计算[J]．公路与汽运，2007(3)：6-7．

Ying Zhong，Tang Rongping，Qiu Zhimin，et al. The Calculation of the Closing Force of Automotive Door[J].Highways & Automotive Applications，2007(3)：6-7．

[6]Huang Z, Wu S, Zhang L. Study of Minimum Door Closing Speed Analysis Method[J]. SAE Technical Paper Series, 2011-01-0782.

[7]Udriste D I, Negrus E M. Construction and Kinematics of Automotive Side Door Latch Mechanisms[J]. SAE Technical Paper Series, 2005-01-0881.

[8]Khakhali A, Nariman-zadeh N, Darvizeh A, et al. Reliability-based Robust Multi-objective Crash Worthiness Optimisation of S-shaped Box Beams with Parametric Uncertainties[J]. International Journal of Crash Worthiness, 2010,15:443-456.

[9]Hines W W, Montgomery D C. Probability and Statistics in Engineering and Management Science[M].3nd Edition.Hoboken: John Wiley & Sons，1990.

(编辑袁兴玲)

Door Closing Force Calculation Considering Door Assembly Deviations

Song KaiLiu JiuwuCheng Aiguo

State Key Laboratory of Advanced Desingand Manufacture for Vehicle Body,Hunan University,Changsha,410082

Abstract:For the inaccurate analyses of automotive door closing force simulation caused by assembling deviations,a approach to accurately calculate the door closing force was proposed.Firstly, by establishing appropriately mechanics model of the components in the process of closing the door, the door lock that impacted the closing force out of several other factors was taken for example, and the probability statistics distribution of door lock’s positional errors in the process of assembling was gained by Monte Carlo simulation.Combined with the door lock’s positional assembling errors in the calculation of the closing force of the mathematical model, the probability distributionof the door closing force was obtained. Then the closing force tests on the prototype were done.The test results show that the calculation accuracy of the door closing force that combined with the door assembling deviations is improved.

Key words:closing force;assembly deviation;Monte Carlo simulation;mechanics model

作者简介：宋凯，男，1981年生。湖南大学汽车车身先进设计制造国家重点实验室副研究员。主要研究方向为汽车车身快速优化设计及疲劳耐久预测。发表论文10余篇。刘九五，男，1990年生。湖南大学汽车车身先进设计制造国家重点实验室硕士研究生。成艾国，男，1972年生。湖南大学汽车车身先进设计制造国家重点实验室教授、博士研究生导师。

中图分类号：U463.8

DOI：10.3969/j.issn.1004-132X.2016.05.006

基金项目：湖南省科技开发计划资助项目(2013TT1006)；广西科技计划重大专项(桂科重1348003-5)；中国博士后科学基金资助项目(2014M552132)；柳州市科技计划资助项目(2013D020201)；湖南大学“青年教师成长计划”资助项目

收稿日期：2015-03-11