空间对接机构捕获锁优化设计

汤树人　陈宝东　刘　仲　康志宇　唐　平

上海宇航系统工程研究所，上海，201109



空间对接机构捕获锁优化设计

汤树人陈宝东刘仲康志宇唐平

上海宇航系统工程研究所，上海，201109

摘要：空间对接机构是实现航天器空间交会对接的关键系统。捕获锁作为对接机构的关键组成部件，具有实现两航天器间捕捉和释放的功能。其中的锁舌弹簧机构是典型的多体系统动力学机构，具有一定的设计难度。针对该问题，分析了锁舌运动规律，简化由分析力学建立的非线性微分方程组，建立了满足工程精度需求的数学模型；接着采用惩罚函数法和随机顺序配对机制改进标准遗传算法，并编制程序完成参数求解；随后应用ADAMS软件进行动力学仿真。捕获锁试验结果表明，捕获力显著减小，性能获得提高。所研制的捕获锁圆满通过了国内载人航天交会对接飞行试验，证明该产品优化设计工作获得了成功。

关键词：空间对接；捕获锁；多体系统；遗传算法；仿真

0引言

空间对接机构是实现载人航天器空间交会对接，以及开展在轨服务的关键系统[1-3]，其中周边式对接机构捕获锁具有实现两航天器间捕捉和释放的功能[4-5]。型号产品研制过程中，对捕获锁上的锁舌弹簧机构有如下要求：对接捕获阶段，要求锁舌能够在卡板器较小的作用力下就压入，并快速弹出完成对卡板器的捕获；对接拉紧阶段，捕获锁能够可靠自锁并承受数千牛的拉力；对接分离阶段，捕获锁解锁后，要求对卡板器仅有数牛的脱离阻力。就空间对接而言，完成捕获是实现对接的先决条件，因此装配在对接机构对接环上的三套捕获锁的性能至关重要。前期经过多轮仿真参数试凑、摸索试验，不断修配锁舌滑槽形状，调整锁舌弹簧机构扭簧和拉簧参数，所设计的捕获锁单个锁舌压入力达34 N。为减小捕获锁锁舌压入力，避免由于捕获力过大而无法快速捕获，并使得空间两飞行器碰撞弹开而导致空间对接失败，就需要对捕获锁开展优化设计工作，从而提高空间对接捕获一次成功率。

1优化设计数学建模

为满足上述空间对接捕获各项要求，采用图1所示的捕获锁结构[6]：锁舌位于捕获锁中部，其受卡板器垂直向下压力，运动轨迹由拉簧、扭簧和卡板器外力综合决定；与此同时，在卡板器下压到底后，由拉簧和扭簧形成的组合弹簧机构提供锁舌自动回弹动力。设计销轴和锁舌等参数，使得处于图1所示位置时，锁舌在销轴约束下处于自锁锁紧状态；在解锁工况时，通过转动手动解锁手柄破坏偏心轴自锁条件，或由电动解锁机构驱动销轴使锁舌脱离自锁位置，卡板器就可以克服拉簧和扭簧较小的阻力而脱离捕获锁锁舌的锁定状态。

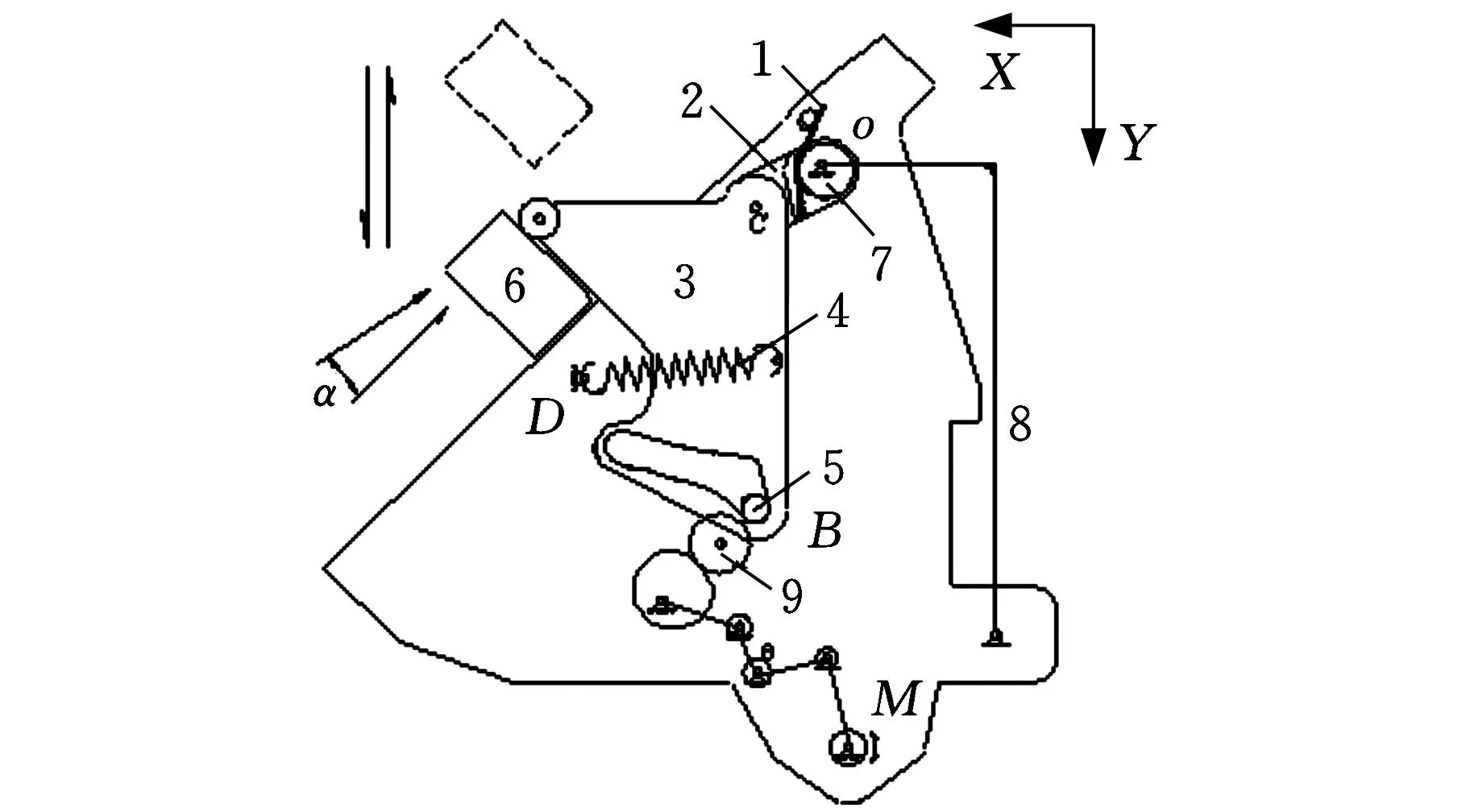
1.扭簧　2.摆杆　3.锁舌　4.拉簧　5.销轴　6.卡板器7.偏心轴　8.手动解锁手柄　9.电动解锁机构图1　捕获锁结构图

捕获锁功能在于实现自动捕获和自锁锁紧。锁舌除两弹簧外无约束的运动可以减小锁舌自动捕获时的压入力，从而使其达到最大的灵活性。因此，建立的数学模型以拉簧的刚度kL、原长l0和扭簧的刚度kN、初始扭矩M04个参数为优化设计对象。预期目标为：确保捕获锁的自动捕获和自锁锁紧功能，并使锁舌在除两弹簧外无其他约束的情况下，具有最大的运动灵活性，反映在测量指标上就是锁舌压入力的值最小。

基于以上想法，首先建立关于锁舌压入力的方程，并将此方程作为目标函数；其次由初始和最终力学平衡关系建立两个约束方程；之后以锁舌回弹时间限制所确定的方程为第三个约束方程。按照文献[7-9]方法建立以上数学模型，其中采用分析力学建立的第三个约束方程为非线性微分方程组，为实现快速求解，故采取简化措施，以建立符合工程精度要求的快速可解模型。

1.1末位置平衡态目标函数的建立

根据锁舌受到卡板器作用力后运动的连续性，以及现有试验数据曲线的直观显示，可以假定锁舌与卡板器相分离、回弹前的那一片刻获得最大的锁舌压入力(该假设由后续的仿真加以初步验证，如果仿真情况与此不符，再进行该目标函数的修改)。根据这一时刻的力学平衡关系，建立压入力目标函数和约束方程。对应锁舌、连杆的受力分析如图2所示。

图2　末位置平衡态受力分析

图2中，坐标原点O为摆杆旋转轴中心，A为锁舌滚轮中心点，B为锁舌与摆杆连接点，C为锁舌与拉簧连接点，D为拉簧与捕获锁基体连接点，图中锁舌处于自锁位置时与销的接触点E未标识。

假设摆杆OB与x轴正向夹角为θ，且如图2所示逆时针方向为正；锁舌简化边线BC与y轴正向的夹角为α，同理假定逆时针方向为正；拉簧DC与x轴正向夹角为β，同理假定逆时针方向为正。

本文中，以l0代表拉簧原长，以θ0代表扭簧不产生扭矩时相对标定零度的转角，以M0代表扭簧预紧扭矩；此外以下标“1”表示初始状态量，以下标“2”表示末状态量。以下捕获锁的基本设计参数为已确定的设计定值：摆杆OB长lOB、锁舌上BC长lBC、AB长lAB、D点坐标(xD，yD)、θ1、α1。

按照基本几何学和力学分析可得：

B点坐标(xB、yB)为

(lOBcosθ,lOBsinθ)

C点坐标(xC、yC)为

(lOBcosθ+lBCsinα,lOBsinθ+lBCcosα)

A点坐标(xA、yA)为

(lOBcosθ+lABcos(α-α1),lOBsinθ+lABsin(α-α1))

扭簧力矩为

M=M0+kN(θ-θ1)

拉簧力为

F′=kL(l-l0)

拉簧长度为

拉簧力F′与x轴的夹角为

β=arcsin((yD-yC)/(xD-xC))

拉簧力F′对于B点力矩长为

lBF=lBCsin(90°-α+β)=lBCcos(α-β)

拉簧力F′对于O点力矩为

MF′O=yCF′cosβ-xCF′sinβ

外力F对于B点力矩长为

lBH=lABsin(45°+α-α1)

外力F对于O点力矩为

MFO=xAFcos45°+yAFsin45°

对B点建立力矩平衡式为

MF′B=MFB

即

F′lBF=FlBH

(1)

对O点建立力矩平衡式为

MF′O+M=MFO

(2)

将以上分析求得量代入相对B点建立的力矩平衡式(1)，整理求得

(3)

将末位置时的参数θ2、α2、β2及A、C点末坐标代入式(3)，并令：

从而得到由末位置确定的目标函数：

F=akL(l2-l0)

(4)

1.2保持末位置平衡约束方程的建立

受力分析及各参量定义、确定与建立末位置平衡态目标函数时相同。

将所求得的各个分析量代入相对O点建立的力矩平衡式(2)，整理求得

(5)

将末位置时的参数θ2、α2、β2及A、C点末坐标代入式(5)，并令：

由此得

F=bkL(l2-l0)+cM0+dkN

(6)

显然，末位置平衡态时，通过相对B点建立力矩平衡式和相对O点建立的力矩平衡式所求得的力大小应该相等，所以由式(6)和式(4)得到一个力平衡约束方程：

g1=(b-a)kL(l2-l0)+cM0+dkN=0

(7)

1.3保持初始位置平衡约束方程的建立

在地面试验时，因为有重力的影响，要求拉簧和扭簧具有一定的初始拉力和扭矩，否则可能会出现锁舌自然下摆一定角度而无法定位在所要求的初始位置的情况。当然，在空间失重条件下，这一个约束条件并不存在。因此，当加入此约束不会较大影响锁舌压入力这一个关键指标时，为方便重力环境下试验则接受该约束；反之，将酌情考虑是否加入该约束。考虑重力环境下初始平衡状态结构图见图3。图3中：m1为摆杆质量，r1为摆杆重心到O点距离，m2为锁舌质量，r2为锁舌重心到过B点铅垂线的距离。

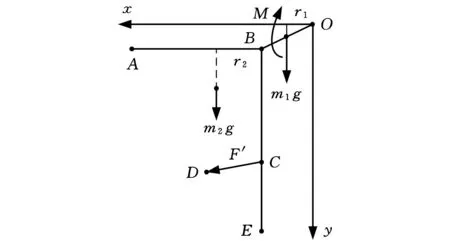
图3　初始位置平衡态受力分析

要防止锁舌和摆杆重力条件下的自然下摆，只需要拉簧力F′和扭簧M 对O点产生的力矩大于重力产生的力矩即可；当有超过时，锁舌受到下端E 处销子的作用力而平衡。

由以上分析结合1.1节分析所得已知量，拉簧力F′和扭簧M 对O点产生的力矩为

M′=M0+kL(l1-l0)cosβ1(lBC+lOBsinθ1)-

kL(l1-l0)sinβ1lOBcosθ1

(8)

重力对O点产生的力矩为

M″=m1gr1cosθ1+m2g(r2+lOBcosθ1)

(9)

由M′-M″>0得到第二个约束方程如下：

g2=M0+kL(l1-l0)cosβ1(lBC+lOBsinθ1)-

kL(l1-l0)lOBsinβ1cosθ1-

m1gr1cosθ1-m2g(r2+lOBcosθ1)>0

(10)

令：

q=(lBC+lOBsinθ1)cosβ1-lOBsinβ1cosθ1

n=m1gr1cosθ1+m2g(r2+lOBcosθ1)

由此得到第二个约束方程：

g2=M0+qkL(l1-l0)-n>0

(11)

1.4锁舌回弹时间约束方程的建立

显而易见，捕获锁捕获运动构件构成了一个二自由度系统，要求得其受到两根弹簧作用力时的准确运动轨迹并最终求得回弹至自锁位置时的时间，可以采用最为基本的分析力学方法。锁舌受力分析如图4所示。图4中，r3为锁舌重心O2与B点距离，φ为BO2与铅垂线方向夹角，J1为摆杆对O点转动惯量，J2为锁舌对B点转动惯量。

图4　锁舌受力分析

系统动能为

(12)

系统势能(在此仅考虑空间失重情况)为

V=0

(13)

由以上得拉格朗日函数:

(14)

拉簧主动力F′(θ,φ)与扭簧主动力矩M(θ)对此系统的虚功δW为

δW=M(θ)δθ+F′(θ,φ)(lOBδθsinθ+lBCδφcosφ)

(15)

为简化工程设计，鉴于实际拉簧与水平夹角β变化很小这一现实情况，在本文中假设其只提供水平方向拉力。

由此得到广义力如下：

Qθ=M(θ)+F′(θ,φ)lOBsinθ

(16)

Qφ=F′(θ,φ)lBCcosφ

(17)

将以上各方程代入拉格朗日方程：

计算化简得

(18)

式(18)即为该系统动力学方程，对其求解后理论上可以得到各个时刻位置对应的相关量，前后运动时间也可以对其进行积分运算而得到。然而，由于式(18)是颇为复杂的非线性微分方程组，实际求解较为困难，考虑到计算效率以及实际工程计算精度需求等各方面因素，提出如下近似回弹时间的计算方法。

首先，实际设计和现有产品锁舌绕B点的旋转角度较小，即φ的始末差值并不大，可将扭簧回复到原始位置的时刻视为锁舌回弹的终止时刻，并不考虑锁舌绕自体旋转所具有的动能，即相当于取消了B处的这一个自由度；然后，将两根弹簧前后的能量差转化为锁舌和摆杆到达终点位置时所具有的动能，由此求得末角速度ω，取其一半为平均角速度ϖ，由θ前后角度差Δθ除以ϖ即可求得近似的回弹时间。显而易见，由此造成的直接影响是计算所得的锁舌回弹角速度过大，因此最后将限定回弹时间乘以一个系数η加以修正。基于以上思路，计算步骤如下：

两弹簧始末位置能量差为

(19)

由M0=kN(θ1-θ0)可以求得

(20)

锁舌和摆杆在末位置时的近似动能为

(21)

由W=T最终求解得

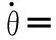
(22)

则锁舌和摆杆回弹时间为

(23)

锁舌回弹时间上限tmax的计算思路为：假定回弹开始那一时刻，与卡板器端角接触点即A点的纵坐标为yA，其值可由该时刻θ和α值代入上文中A点坐标公式求得；卡板器向下运行至终点时，其端角Z点纵坐标yZ不难从现有设计图纸中获得；从飞船对接初始条件中可以找到所需要的对接速度，在此加严设计，取卡板器向下运行速度最大值为v ；由此得到锁舌回弹时间上限计算式：

(24)

将以上各式代入t <ηtmax(可以先取η值为0.85，视后续应用遗传算法优化计算结果再行修改)，运算化简得

(25)

令：

e=l2-l1f=l2+l1

g=(θ2-θ1)2h=2(θ2-θ1)

由此得到第三个约束方程为

g3=ekL(f-2l0)+gkL+hM0-p>0

(26)

1.5待定变量消参

综合整理可以看出：以上各个分量和方程式在终止位置θ2和α2确定时都可以唯一确定，由此对末态值后续应用算法模糊预估时就能进行程序运算。

进一步由锁舌与卡板器结构简图(图5)可以分析得到，锁舌产生回弹动作时，锁舌与卡板器接触点A，都在图示过卡板器角点F(xF、yF)的铅垂线上(考虑锁舌上滚轮半径r的影响则应为xF-r)。由此可以依据几何运动关系将θ2与α2中的一个量用另一个来表示，从而减少算法模糊预估参数数量。

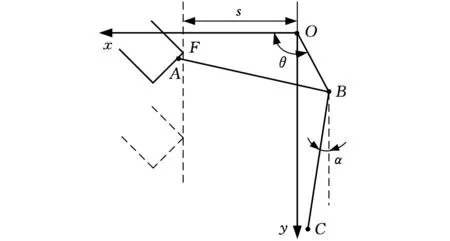
图5　锁舌与卡板器结构简图

由结构简图可以列出以下关系式：

xF-r=xA2=lOBcosθ2+lABcos(α2-α1)

(27)

解得：

(28)

由以上分析得出如下结论：在对拉簧刚度kL、原长l0和扭簧刚度kN、初始扭矩M04个参数进行优化设计的时候，只需要输入终止位置估计量α2，就可以实现目标函数、约束方程求解。

2遗传算法优化求解

遗传算法(geneticalgorithm,GA)是把自然遗传学和计算机科学结合起来的优化方法，可以在整个可行域里进行随机寻优,能够很好地解决一般优化算法所存在的局部最优问题，典型遗传算法流程包含选择、交叉和变异等运算[10-11]。为使遗传算法与所述的工程问题实现衔接，按照所建立的数学模型，设计捕获锁适应度函数如下：

G=100-AF-A1g1-A2g2-A3g3

(29)

即设定适应度最大值为100；同时按照F、g1、g2和g3项目的紧要程度设定A、A1、A2和A34个对应权系数数值。

在遗传算法中，由于运算中的选择对应的是整个群体，因此需要设计一个好的算法，使得选择运算尽可能随机，从而避免多代优化后，在整个群体内显示出“近亲繁殖”的规律，导致运算收敛性不佳[12]。与此同时，为提高程序计算效率，选择运算只有兼具随机性和规律性，才能使所编制的遗传算法程序在实现运算收敛性的同时，又能高效性运行。对于该选择算法设计难题，本文设计基于随机顺序配对机制的选择算法流程[13]。

如图6所示，采用循环链表形式作为初始种群的初始数据库表达结构，从而构成一个闭环的群体。利用随机数生产函数，随机选择其中的一个个体，标志为K。此后，沿顺时针、逆时针两个方向依次选择个体，将个体K-1和K+1作为后续交叉和变异运算的母体，依次类推顺序配对。从该选择算法可以看出，由于每代选择运算时，都是随机抽取一点，可以避免选择机制出现规律性，从而影响进化运算效果；同时又在确定该点之后，所有选择均按照指针顺序移动定位，从而保障了选择运算的高效性。

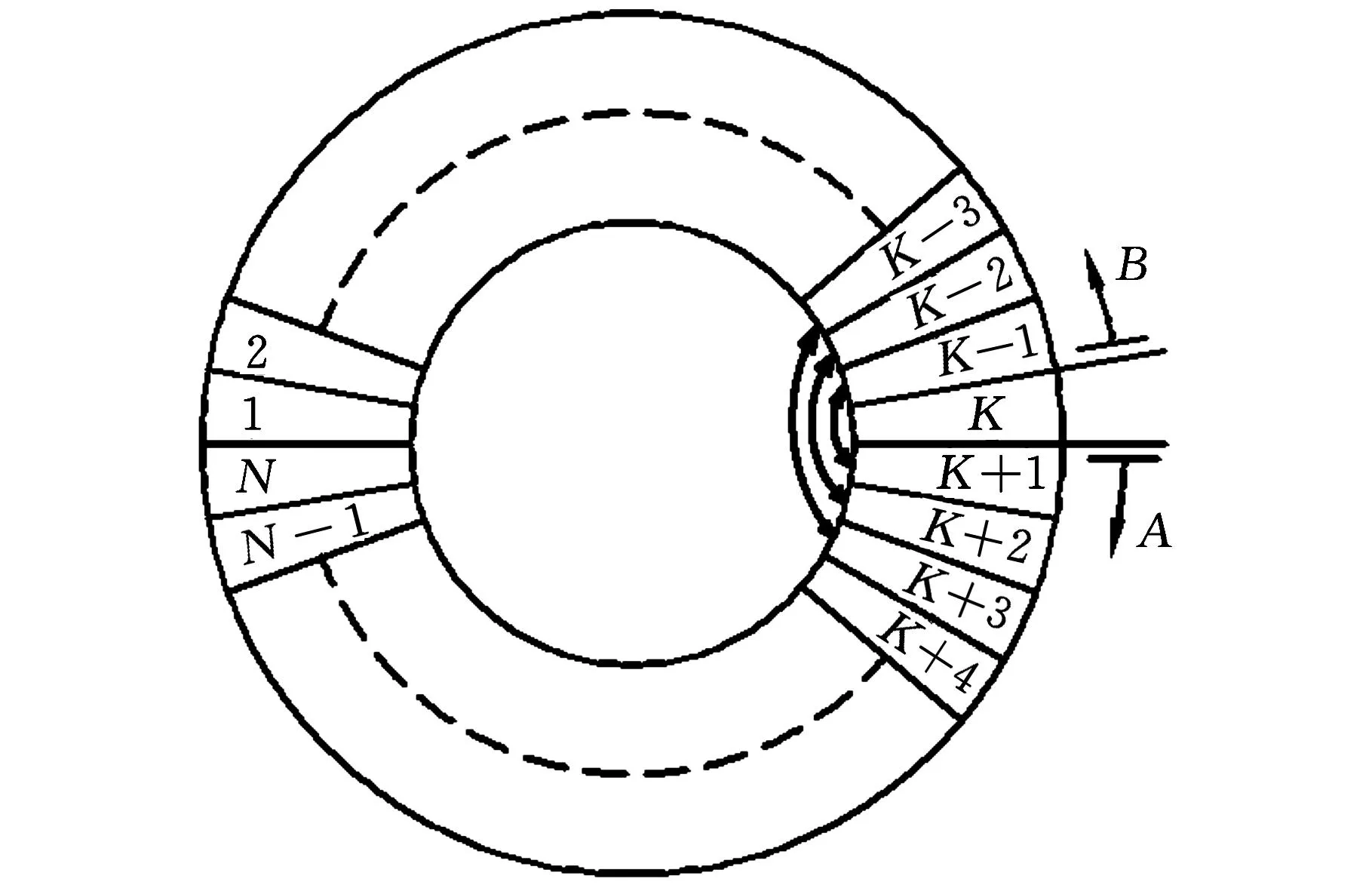
图6　选择算法流程

按照以上基于循环链表进行初始种群选择，构建随机顺序配对机制，改进的遗传算法程序能在1 s内完成程序自检、运算，输出拉簧和扭簧各个优化参数值，并求出对应的锁舌最大压入力F=6.534 N。

3仿真分析复核

目前仿真技术已成为产品设计研究的有效手段，能够有效降低系统研制成本，降低由于设计不当就工程实施投产所存在的风险[14-16]。对此，利用Pro/Engineer软件构建模型后，导入ADAMS动力学仿真系统，并将以上计算得到的优化参数值作为仿真输入，施加运动副、约束和载荷等项目后，进行捕获锁动力学仿真，仿真过程如图7所示。

输出仿真结果曲线，如图8所示，且设定图7a所示位置为卡板器垂直下行位移s的零点，在零点位置接触瞬间，由于设定卡板器以200 mm/s下行运动，与锁舌发生碰撞，因此产生瞬间冲击，该数值约5.451 N，之后振荡衰减，符合碰撞效应。

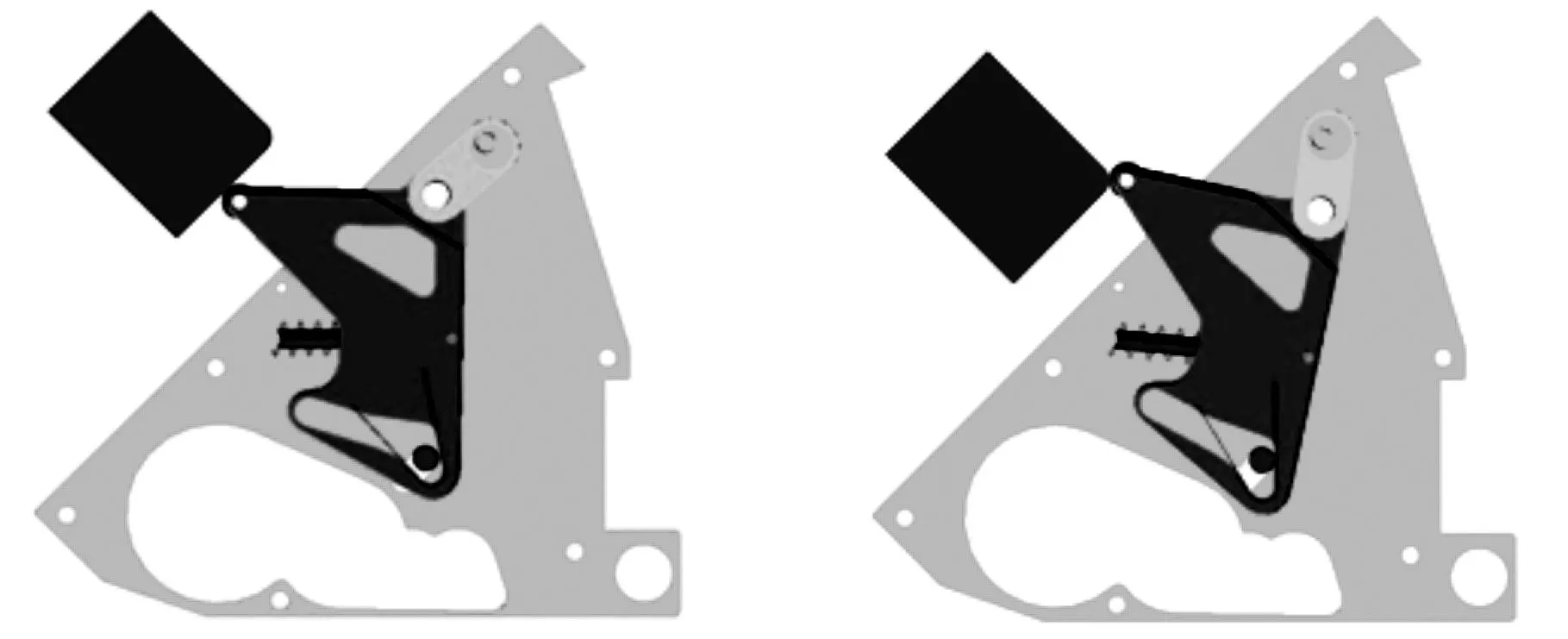
(a)卡板器下压锁舌(b)锁舌最大运动角

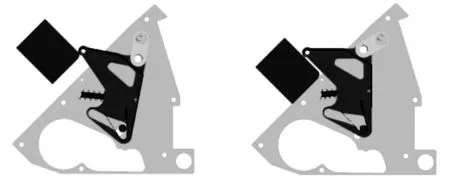
(c)锁舌回弹(d)捕获完成图7　仿真过程

图8　捕获压入力仿真曲线

从捕获力仿真曲线可以看到锁舌压入力F峰值为6.197 N，相比遗传算法程序6.534 N计算值，偏小近5%，分析其原因如下。

(1)输入的终止位置α2为预估量，初始程序运算与仿真测量值有差异，使得锁舌的最大位移得以减小，表现在锁舌压入力上就是所得到的仿真值小于遗传算法程序计算值；

(2)遗传算法程序计算所对应的数学模型，在锁舌回弹时间约束方程的建立过程中，为避免求解复杂非线性微分方程，采用了工程简化处理方法，因此将引入一定的计算偏差。

4优化设计后试验

经一系列优化设计，投产并装配三套捕获锁，每套捕获锁均采取双锁舌设计以提高捕获可靠性，并研制测试装置进行测试工作，如图9所示。

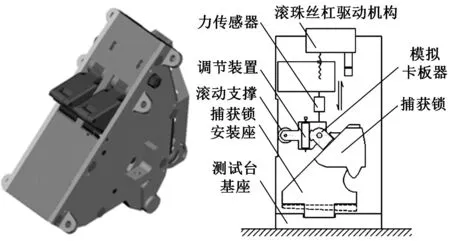
图9　捕获锁及测试装置设计

通过试验，测得三套捕获锁捕获力曲线如图10所示，从中可以看到双锁舌捕获锁的最大捕获压入力F为17.2 N，平均单锁舌压入力为8.6 N，相比理论值增大近30%。原因在于：为确保锁舌回弹时间小于50 ms指标要求，拉簧、扭簧参数均往上取整，以及由于锁舌机构运动摩擦的存在，使捕获压入力增大。总体而言，相比早前单锁舌压入力34 N，大幅减小，显著提高了捕获锁锁舌的运动灵活性。

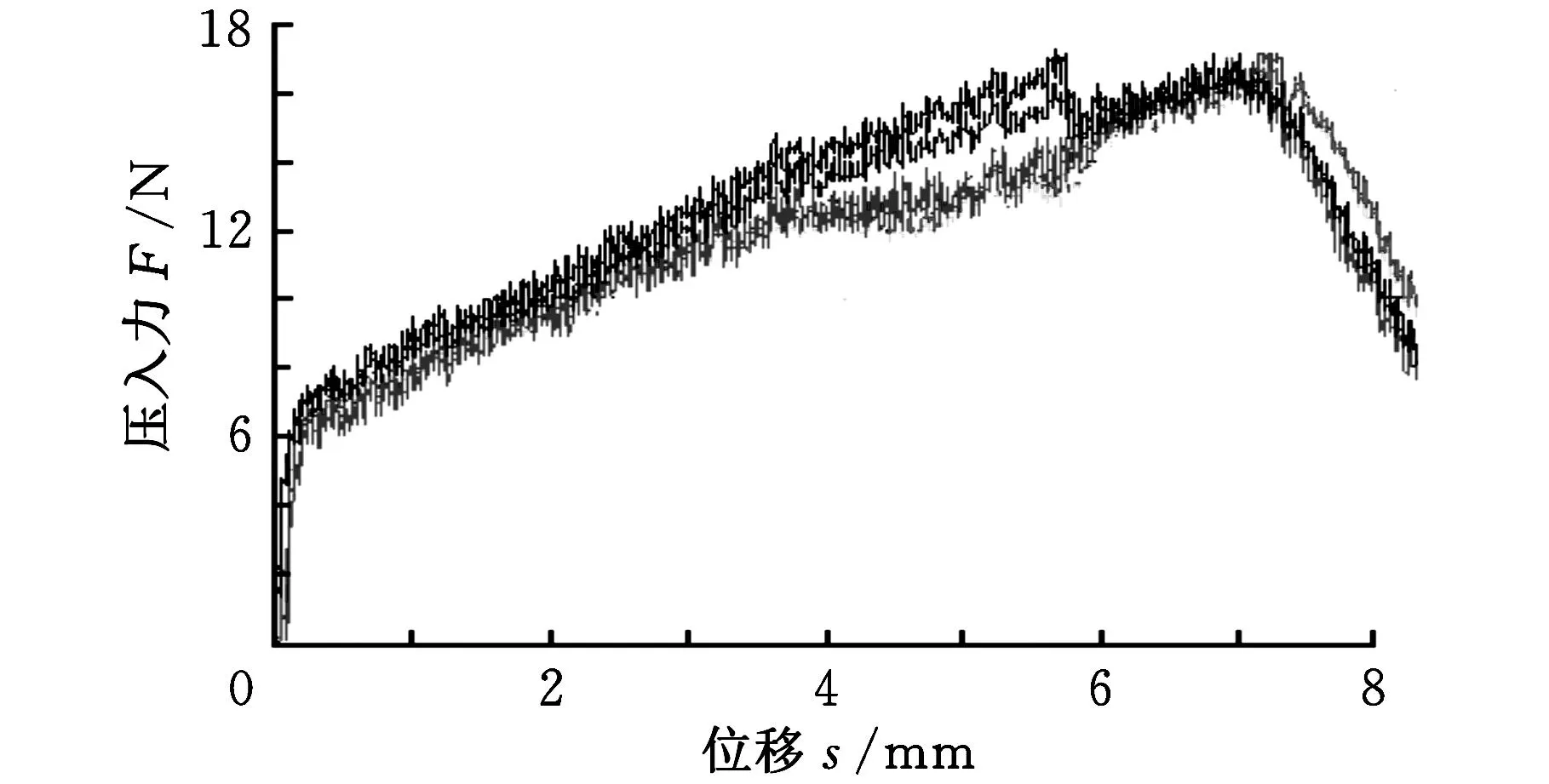
图10　捕获锁捕获压入力测试曲线

最后，将所研制的捕获锁装配至周边式对接机构中，并于2011年11月在实现的“神舟八号”飞船与“天宫一号”目标飞行器的首次交会对接中一次捕获成功；后续所研制的捕获锁产品又在“神舟九号”和“神舟十号”中得以应用，并圆满完成飞行试验，表明捕获锁产品研制工作获得了成功。

5结束语

本文对周边式对接机构捕获锁设计进行分析，首先，建立数学模型；接着，在满足工程需要的前提下，进行了简化处理，避免反复优化计算时求解复杂非线性微分方程这一难题；随后，利用循环链表、采用随机顺序配对机制，改进编制遗传算法程序，实现多参数优化问题快速求解；之后，进行产品仿真分析和试验测试工作，有效改善了捕获锁产品性能；最终，所研制的捕获锁产品成功完成了国内首次交会对接等三次在轨飞行试验，为我国载人航天工程的顺利实施和后续空间站工程的建设和运营作出了贡献。

参考文献：

[1]Sullivan B R．Technical and Economic Feasibility of Telerobotic On-orbit Satellite Servicing[D]．Maryland：Univ．of Maryland Space Systems Laboratory，2005．

[2]Motaghedi P，Stamm S．6 DOF Testing of the Orbital Express Capture System[J]．SPIE，2005，5799：66-81．

[3]陈小前，袁建平，姚雯，等．航天器在轨服务技术[M]．北京：中国宇航出版社，2009．

[4]娄汉文，曲广吉，刘济生．空间对接机构[M]．北京：航空工业出版社，1992．

[5]Michael F M，Gurpartap S S．Rendezvous and Docking for Space Exploration[C]//The AIAA 1st Space Exploration Conference．Orlando：AIAA，2005：1-10．

[6]上海宇航系统工程研究所．捕获锁：中国，ZL200510001546．X[P]．2013-01-02．

[7]王勖成．有限单元法[M]．北京：清华大学出版社，2003．

[8]李东旭．高等结构动力学[M]．2版.北京：科学出版社，2010．

[9]王其藩．高级系统动力学[M]．北京：清华大学出版社，1995．

[10]Goldberg D E．Genetic Algorithms in Search，Optimization and Machine Learning[M]．New Jersey：Addison-Wesley Publishing Company，1989．

[11]董德威，颜云辉，张尧，等．矩形件优化排样的自适应遗传模拟退火算法[J]．中国机械工程，2013，24(18)：2499-2504．

Dong Dewei，Yan Yunhui，Zhang Yao，et al．Adaptive Genetic Simulated Annealing Algorithm in Optimal Layout of Rectangular Parts[J]．China Mechanical Engineering，2013，24(18)：2499-2504．

[12]Hochbaum D S．Approximation Algorithm for NP-hard Problems[M]．London：An International Thomson Publishing Company，1998．

[13]汤树人，陈宝东，柏合民，等．遗传算法在空间对接机构优化设计中的应用[J]．宇航学报，2008，29(2)：139-143．

Tang Shuren，Chen Baodong，Bai Hemin，et al．The Application of Genetic Algorithm in Space Docking Mechanical Optimization[J]．Journal of Astronautics，2008，29(2)：139-143．

[14]陈军．MSC．ADAMS技术与工程分析实例[M]．北京：中国水利水电出版社，2008．

[15]倪俊，徐彬．基于ADAMS的FSAE赛车建模与操纵稳定性仿真[J]．工程设计学报，2011，18(5)：354-358．

Ni Jun，Xu Bin．Modeling and Handling Stability Simulation of a FSAE Racing Car Based on ADAMS[J]．Journal of Engineering Design，2011，18(5)：354-358．

[16]马立峰，王刚，黄庆学，等．复合连杆机构复演滚动轨迹的特性研究[J]．中国机械工程，2013，24(7)：877-881．

Ma Lifeng，Wang Gang，Huang Qingxue，et al．Research on Properties of Compound Linkage Recapitulation Rolling Trace[J]．China Mechanical Engineering，2013，24(7)：877-881．

(编辑袁兴玲)

Optimization Design of Capture Latch in Space Docking Mechanism

Tang ShurenChen BaodongLiu ZhongKang ZhiyuTang Ping

Aerospace System Engineering Shanghai，Shanghai，201109

Abstract：Space docking mechanism was an important portion to realize space docking between aircrafts. As a key component of docking mechanism, capture latches were used to carry out following actions: capture and release. The bolt-spring mechanism in capture latch was quite hard to design as a typical multi-object system. This paper analyzed the movement orderliness of bolt-spring mechanism and built its mathematics model, then simplified those nonlinear equations on the basis of engineering requirements. After that, penalty function and stochastic tactic distribution model were used to improve the standard genetic algorithm, and the calculations were completed and the results were checked by ADAMS simulation method. At last，capture latch tests indicate that capture force reduces and capability improves observably. Finally, capture latch put across China on-orbit space docking test, and attested upwards optimization design successfully.

Key words：space docking; capture latch; multi-object system; genetic algorithm; simulation

作者简介：汤树人，男，1981年生。上海宇航系统工程研究所高级工程师。主要研究方向为空间机构优化与在轨服务总体设计。获发明专利10项，发表论文10篇。陈宝东，男，1968年生。上海宇航系统工程研究所研究员。刘仲，男，1979年生。上海宇航系统工程研究所高级工程师。康志宇，男，1976年生。上海宇航系统工程研究所研究员、博士。唐平，男，1970年生。上海宇航系统工程研究所研究员。

中图分类号：TH122

DOI：10.3969/j.issn.1004-132X.2016.05.008

基金项目：国家载人航天空间交会对接工程;上海市科技人才计划项目(14XD1423400)

收稿日期：2015-02-27