大兆瓦级风电齿轮箱耦合动态特性及结构噪声分析

杨长辉　徐涛金　吴灿元

1.重庆理工大学汽车零部件先进制造技术教育部重点实验室，重庆，4000542.重庆齿轮箱有限责任公司，重庆，402263



大兆瓦级风电齿轮箱耦合动态特性及结构噪声分析

杨长辉1徐涛金1吴灿元2

1.重庆理工大学汽车零部件先进制造技术教育部重点实验室，重庆，4000542.重庆齿轮箱有限责任公司，重庆，402263

摘要：风电齿轮箱是风电机组的重要组成部分，其动态性能的好坏直接影响整个机组的性能。建立了具有两级行星加一级平行轴齿轮传动的大兆瓦级风电齿轮箱齿轮-传动轴-轴承-箱体系统耦合非线性动力学有限元模型，采用Lanczos法对齿轮箱系统进行耦合模态分析。在综合考虑直斜齿轮时变啮合刚度、齿轮误差及齿轮啮合冲击等内部激励因素综合作用影响下，运用直接积分法对整个风电齿轮箱系统进行了动态响应求解，从而获得齿轮箱各点的振动位移、速度及加速度动态评价指标，并且对系统结构噪声进行了分析。研究结果可为大兆瓦级风电齿轮箱的动态性能优化提供参考。

关键词：风电齿轮箱；内部激励；动态响应；结构噪声

0引言

增速齿轮箱是风力发电机组重要的传动部件，其传动的稳定性、可靠性及动态性能关系到整个风电系统的正常运行。随着风电增速齿轮箱向大兆瓦级方向的发展，齿轮在重载工况且伴随外部变载荷作用下，齿轮箱的振动性能及噪声预估就显得尤为重要。国内外学者从数学模型和有限元模型等方向对此进行了大量研究。Abboudi等[1]在考虑内外激励源作用下采用集中质量法建立了12自由度的风电齿轮箱动力学微分方程，以研究参变量对齿轮箱振动特性的影响。Helsen等[2]采用多种柔刚度耦合方式对齿轮箱系统动态特性进行了对比分析。Kahraman[3]建立了复合行星轮系动力学模型并进行了自由扭转振动特性的研究分析。马辉等[4]利用转子系统有限元模型和斜齿轮集中质量模型相结合的方式，通过修改啮合刚度矩阵研究了系统模态变化规律。Abbes等[5]针对齿轮箱在时变刚度激励下采用声固耦合方法进行了声辐射分析。由于风电齿轮箱系统非线性耦合效应、传递误差及冲击载荷等因素的存在，采用传统数值解析法进行分析计算变得十分复杂，而有限元法有利于齿轮箱系统动态特性分析及噪声评估[6-7]。

本文综合考虑齿轮啮合刚度激励、误差激励及啮合冲击激励等内部激励因素，建立大兆瓦级风电齿轮箱非线性耦合有限元模型，研究在内部激励作用下齿轮箱系统的动态响应特性及预估系统结构噪声。

1大兆瓦级风电齿轮箱耦合有限元模型

1.1风电增速齿轮箱传动原理

5 MW大功率分流风电增速齿轮箱传动原理如图1所示。该齿轮箱由行星架输入并驱动行星轮带动太阳轮转动，太阳轮输出作为下一级齿轮传动的输入。系统包含两级行星轮系统和一级平行轴齿轮传动。行星轮传动系统结构属于NGW型，输入级行星系统作为低速级，由5个行星直齿轮内啮合传动，第二级行星系统作为中速级，由3个行星斜齿轮内啮合传动，输出级作为高速级，由斜齿轮外啮合传动。该增速齿轮箱齿轮传动参数见表1。

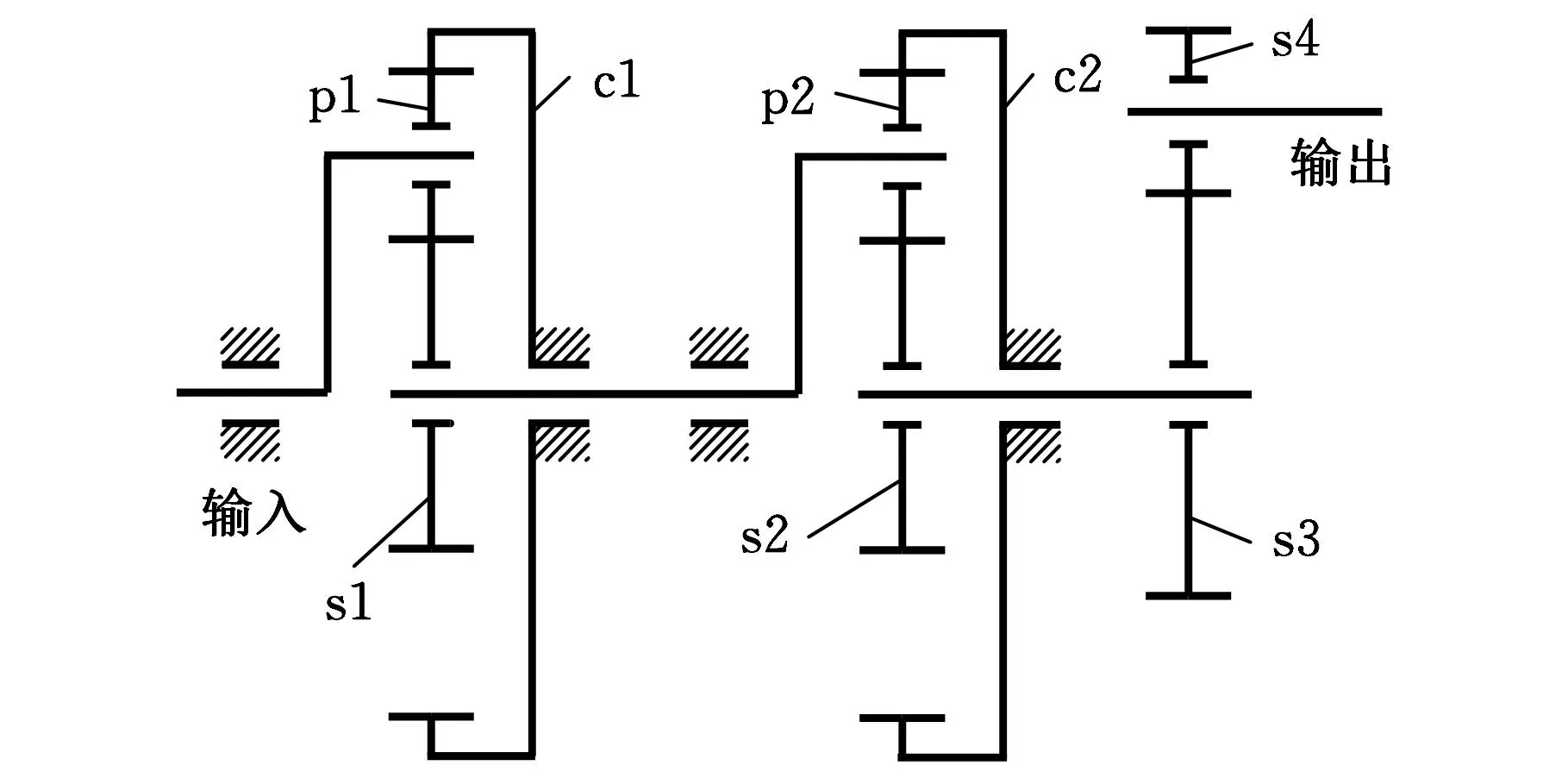
pi、si、ci分别表示行星轮、太阳轮和内齿圈；i=1,2，表示齿轮传动级数；s3表示输出大齿轮；s4表示输出齿轮轴图1　5 MW风电增速齿轮箱传动原理图

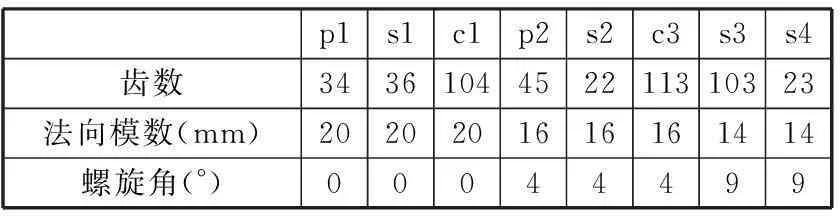
p1s1c1p2s2c3s3s4齿数3436104452211310323法向模数(mm)2020201616161414螺旋角(°)00044499

1.2风电增速齿轮箱有限元模型

风电增速齿轮箱结构比较复杂，建立系统实体模型时对某些部件作了相应的简化处理，如太阳轮与行星架处的花键连接用圆孔配合作等效处理。为了改善网格质量，在建模时忽略了螺栓孔、键槽、小圆弧和倒角等小特征，上述简化处理方式并不影响系统有限元分析的准确程度。根据该增速齿轮箱结构及各级齿轮传动参数，建立系统三维实体模型，该增速齿轮箱系统实体模型及内部传动结构模型分别见图2、图3。

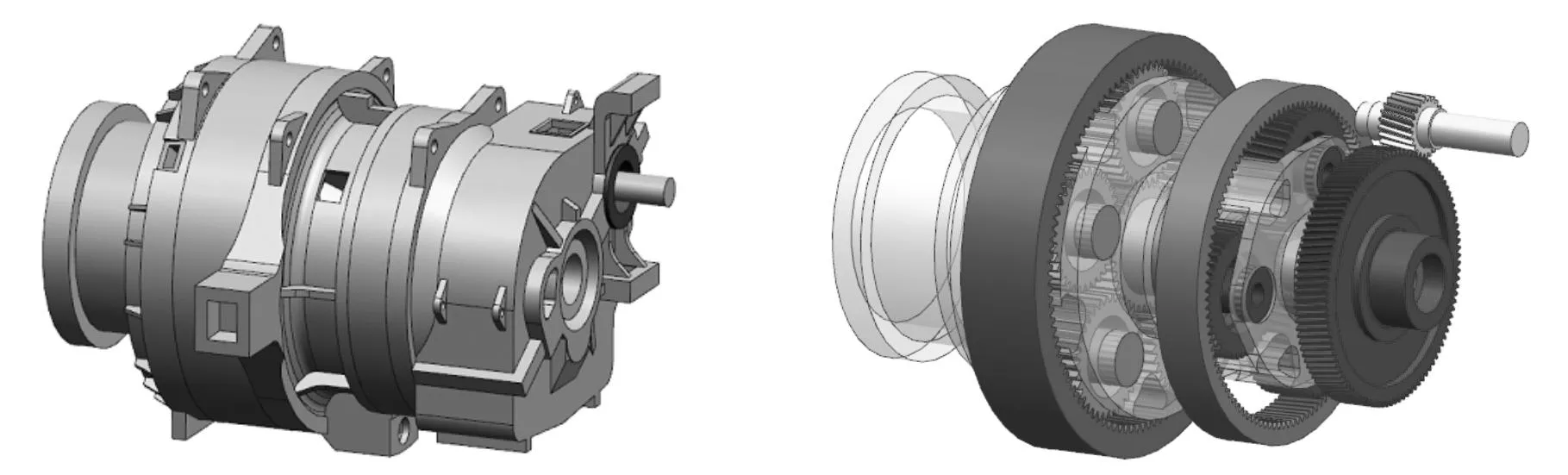
图2　齿轮箱系统实体模型图3　传动系统实体模型

根据已建立的风电增速齿轮箱实体模型，采用前处理有限元软件Hyper mesh对实体进行网格划分。对齿轮等规则零部件，划分六面体单元并赋予单元类型为C3D8I，对箱体等不规则零部件，划分四面体单元并赋予单元类型为C3D10，网格数量共计583 800单元、623 471节点。

在系统有限元模型中，啮合齿轮副用弹簧单元连接，箱体轴承座内表面与传动部件及行星轮与行星轮轴之间用弹簧单元模拟轴承，轴承用4个弹簧单元模拟，4个弹簧单元呈“十”字形分布，弹簧刚度由生产厂家提供。对输入输出部件释放转动自由度，支撑臂完全约束作为边界约束条件。建立齿轮-传动轴-轴承-箱体耦合非线性动力学有限元模型，如图4所示。

图4　齿轮箱耦合有限元模型及原理图

2系统内部动态激励求解

2.1齿轮啮合动力学微分方程

把一对啮合齿轮传动副简化为图5所示的振动系统，则齿轮传动的非线性动力学方程[8]表示为

(1)

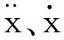
图5　系统振动模型

不考虑外部激励，则式(1)可变为

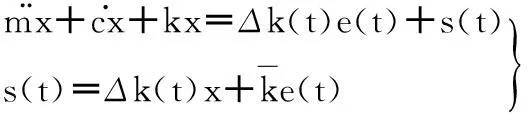
(2)

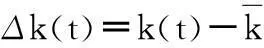
齿轮内部动态激励由时变刚度激励、误差激励和啮合冲击激励组成，则内部动态激励为

Ft=Δk(t)e(t)+s(t)

(3)

2.2齿轮时变啮合刚度激励

2.2.1直齿轮时变啮合刚度计算

计算直齿轮时变啮合刚度的方法通常有材料力学法、弹性力学法和有限元法。本文采用材料力学法中的石川法。由于直齿轮副啮合存在单双对齿啮合过程，在两啮合区交替时啮合刚度产生突变，并且啮合过程中同时参与啮合的轮齿对数随时间作周期变化，因此时变刚度曲线表现为方波形和周期性。低速级行星直齿轮系统中的太阳轮与行星轮以及行星轮与内齿圈的时变啮合刚度激励曲线如图6所示。

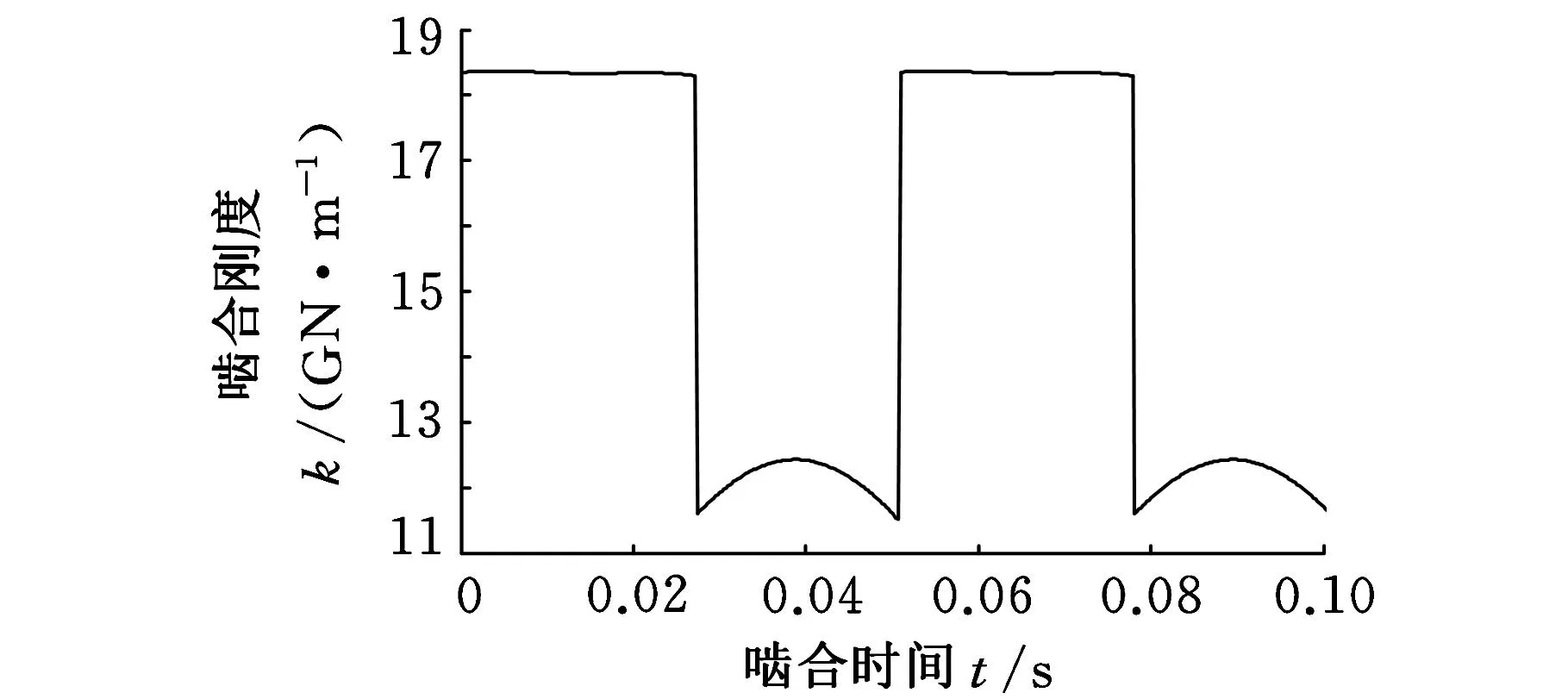
(a)太阳轮与行星轮啮合刚度激励

(b)行星轮与内齿圈啮合刚度激励图6　低速级直齿轮时变啮合刚度曲线

2.2.2斜齿轮时变啮合刚度计算

关于斜齿轮轮齿啮合刚度计算，可以通过研究接触线长度变化来计算齿轮瞬时啮合刚度的变化[9]，从而计算出斜齿轮轮齿啮合刚度。设齿轮在某段时间内转过的齿数为n，则轮齿啮合周期Tz与时间t的关系为

n=t/Tz

(4)

设k0为斜齿轮啮合副接触线上的一单位长度所具有的啮合刚度，视为一常数，则斜齿轮啮合副上的变啮合刚度k(n)与啮合接触线长度L(n)存在的关系式为

k(n)=k0L(n)

(5)

设n=0时接触线刚进入啮合平面，端面重合度εa大于轴向重合度εb时，瞬时接触线长度为

L(n)=B0(n)b/cos(β b)

(6)

式中，B0(n)为啮合线长度系数；b为齿宽；β为基圆螺旋角。

通过傅里叶级数变换可得

a0=2εa/p

cos(2πjεb/p)-cos[2πj(εa+εb)/p]-1}

sin(2πjεb/p)-sin[2πj(εa+εb)/p]}

式中，p为同时啮合的最大齿对数。

中速级太阳轮和行星轮、行星轮和内齿圈以及高速级输出齿轮副的斜齿轮时变啮合刚度激励分别如图7、图8所示。

(a)太阳轮和行星轮啮合刚度激励

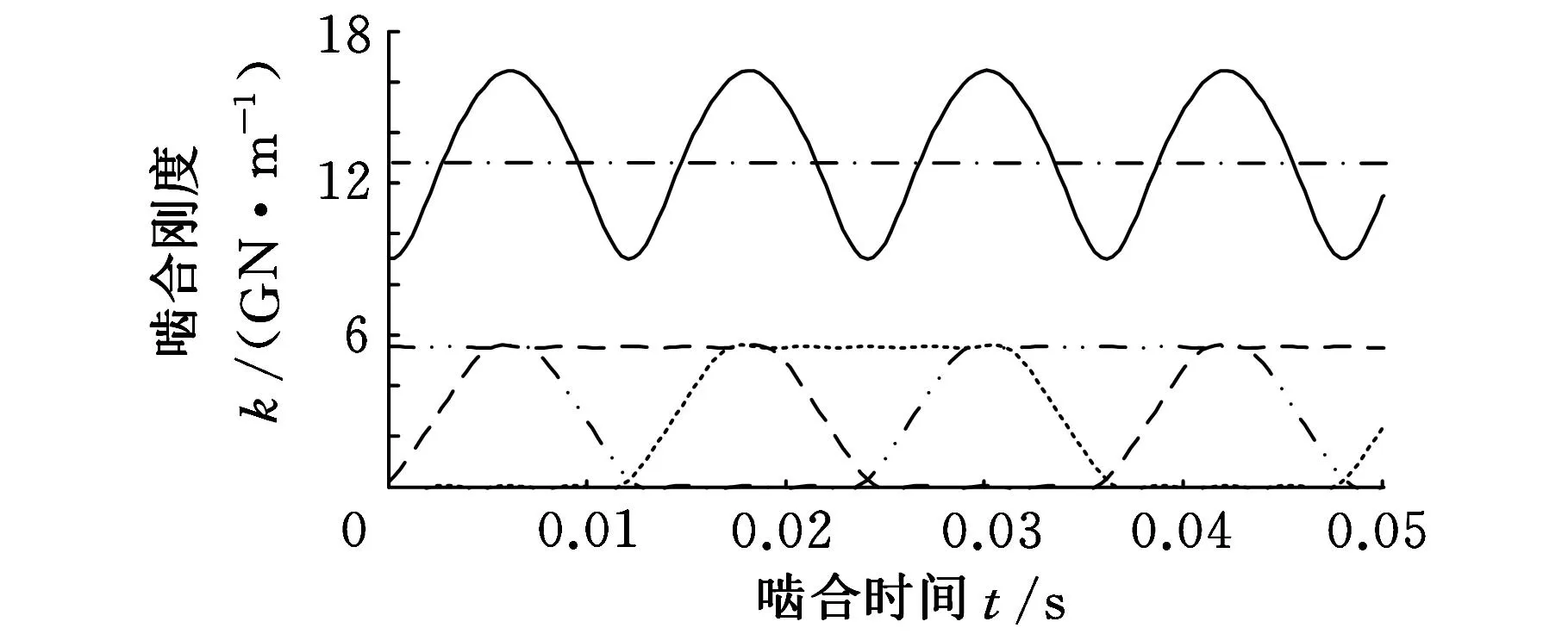
(b)行星轮和内齿圈啮合刚度激励

图7　中速级斜齿轮啮合刚度激励曲线

图8　高速级斜齿轮副啮合刚度激励

2.3齿轮误差激励

齿轮啮合误差是由齿轮加工误差和安装误差引起的，会导致齿轮啮合齿廓偏离理论的理想啮合位置，使齿轮瞬时传动比发生变化，造成轮齿之间的碰撞和冲击，产生齿轮啮合的误差激励。对于误差激励，采用简谐函数来模拟。齿轮的偏差根据齿轮设计精度等级来确定，则齿轮的齿形误差和基节误差可用正弦函数表示为

e(t)=e0+ersin(2πt/Tz+φ)

(7)

式中，e0、er分别为轮齿误差的常值和幅值；φ为相位角。

对于风电齿轮箱低速级、中速级和高速级齿轮，根据精度等级分别计算得到图9所示的误差激励曲线。

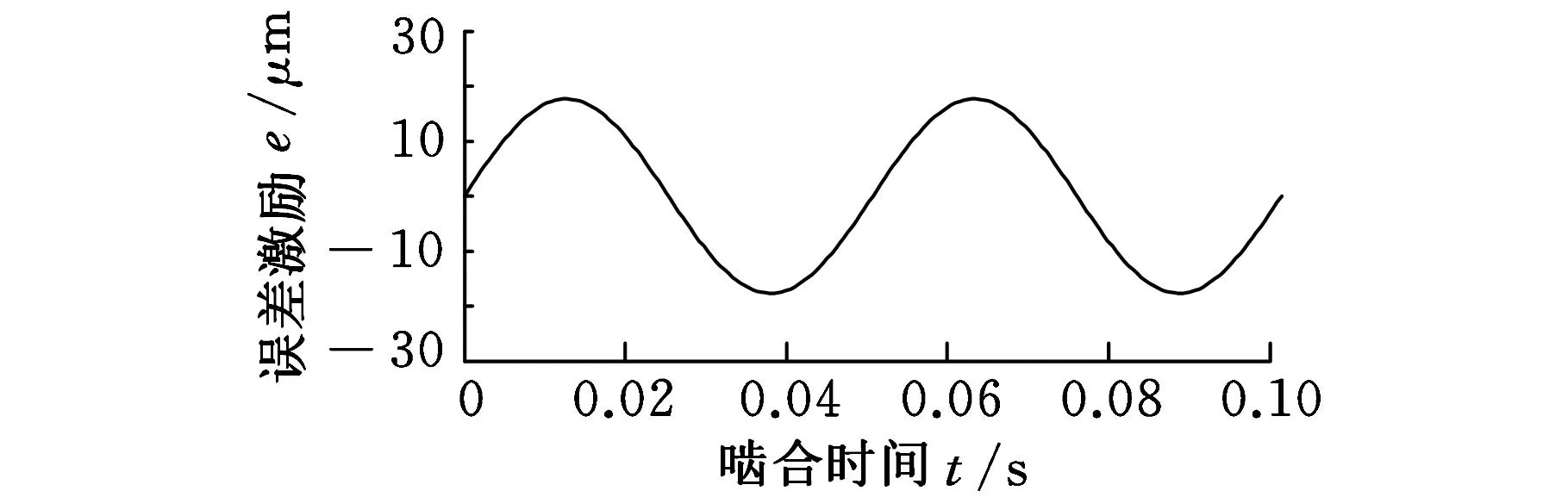
(a)低速级

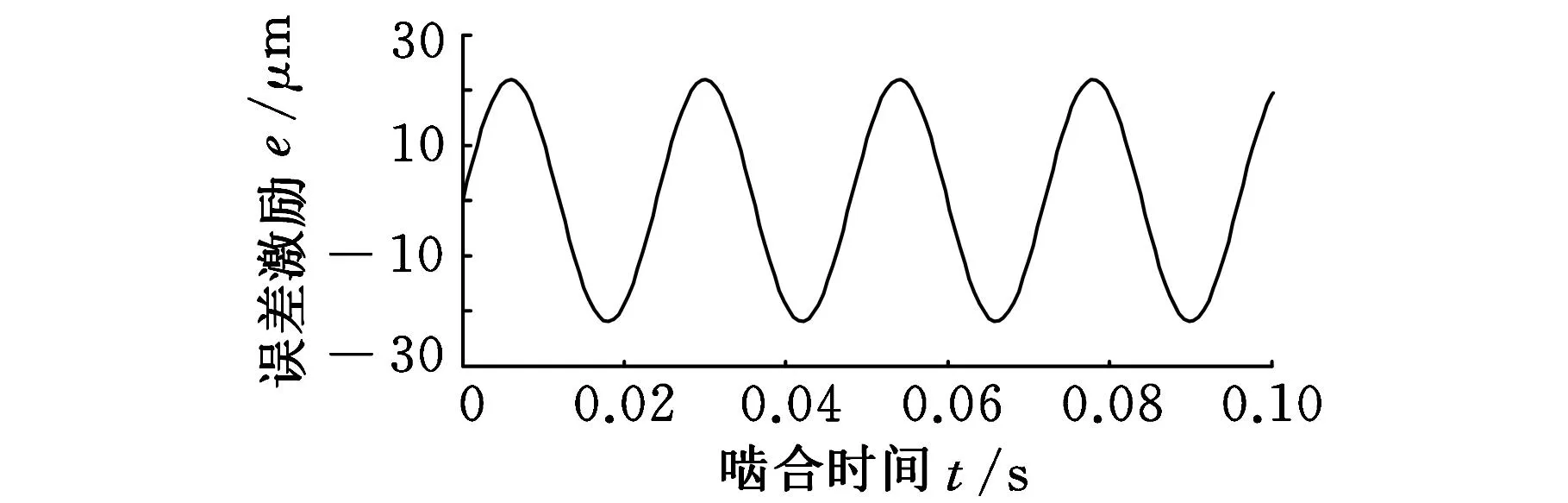
(b)中速级

(c)高速级图9　各级齿轮误差激励曲线

2.4齿轮啮合冲击激励

啮合冲击激励包括啮入冲击和啮出冲击。这是因为齿轮在啮合过程中，轮齿发生变形以及轮齿存在误差导致轮齿产生基节误差，使齿轮在啮入和啮出时偏离理论啮合线而引起了啮入和啮出冲击。本文只考虑齿轮啮入冲击，采用齿轮接触动力学有限元法仿真计算求得[10]。风电增速齿轮箱各级齿轮啮入冲击激励分别如图10所示。

2.5内部动态激励

由式(3)可知，齿轮内部动态激励包括啮合刚度激励、误差激励和冲击激励。将齿轮啮合刚度的变刚度部分与齿轮综合误差相乘，再加上冲击激励就可得到合成动态激励。风电增速齿轮箱各级齿轮内部动态激励合成曲线如图11所示。

3风电齿轮箱动态特性分析

3.1风电齿轮箱耦合模态分析

在有限元模态分析中，系统的固有特性(固有频率和固有振型)与约束状态有关，而与所受外载荷无关。齿轮箱系统自由振动微分方程为

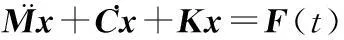
(8)

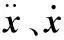
(a)低速级

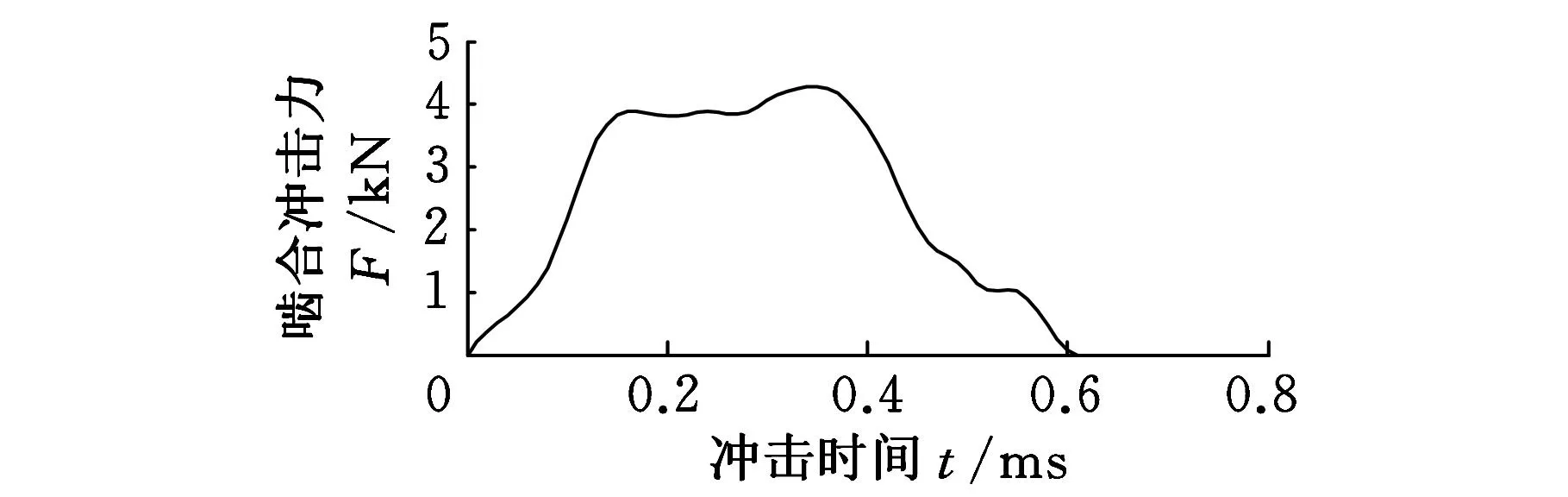
(b)中速级

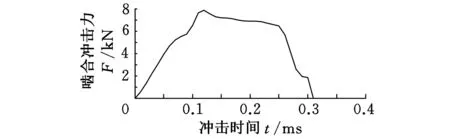
(c)高速级图10　各级齿轮啮入冲击激励曲线

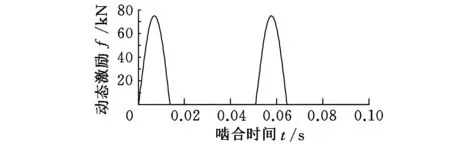
(a)低速级

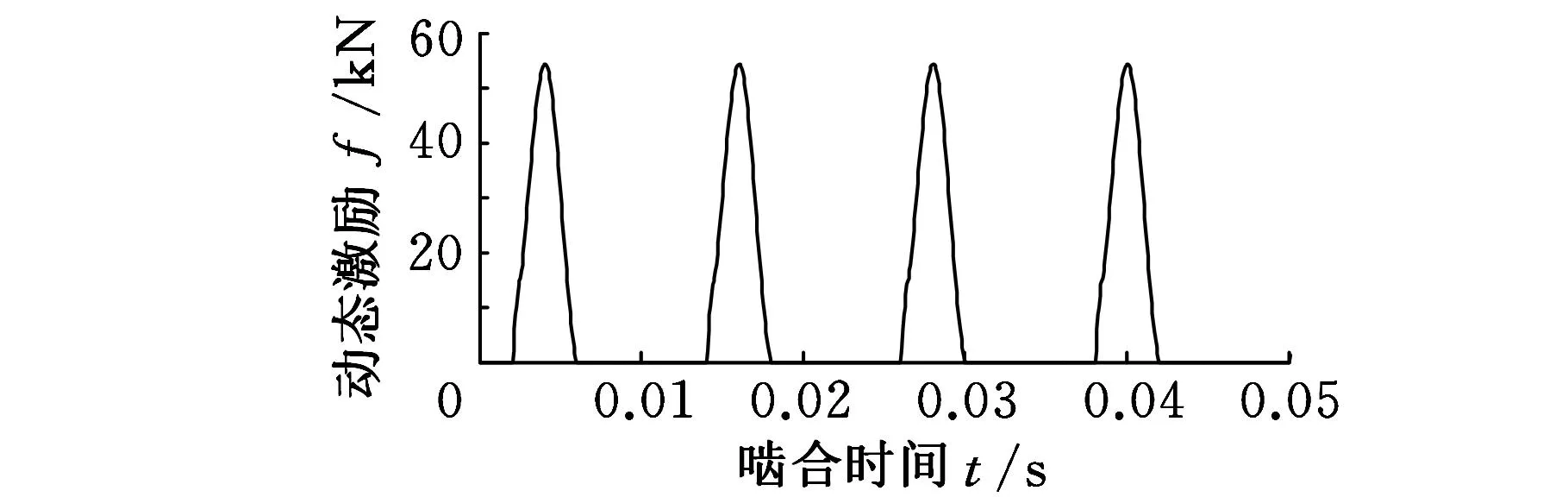
(b)中速级

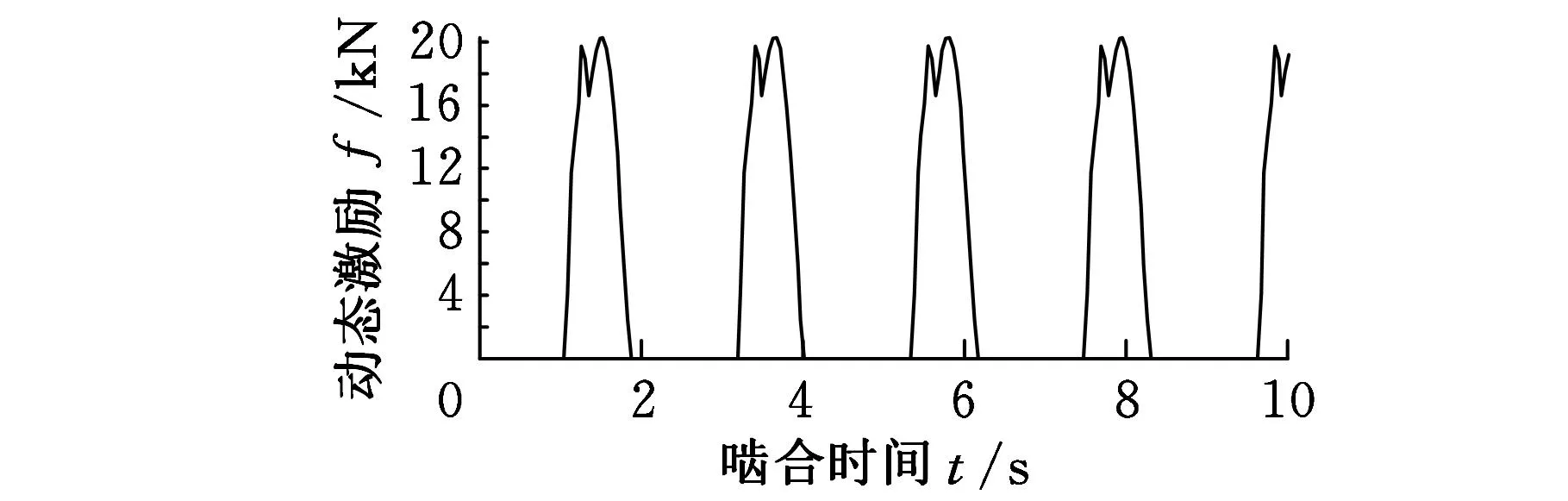
(c)高速级图11　各级齿轮副内部动态激励合成曲线

本文采用Lanczos方法在ABAQUS有限元软件中对风电齿轮箱系统进行约束模态求解。得到前10阶固有频率和振型，表2列出了前10阶固有频率及其对应振型。图12为第1阶和第2阶固有振型图。

该齿轮箱输入转速为11.38r/min，在此转速下低速、中速和高速级齿轮啮合频率分别为19.73Hz、83.35Hz和466.19Hz。高速级齿轮啮合频率与系统第44阶固有频率464.68Hz十分接近，产生共振现象，因高阶振型对结构实际振动贡献量非常小，对齿轮系统结构不会造成较大的危害。

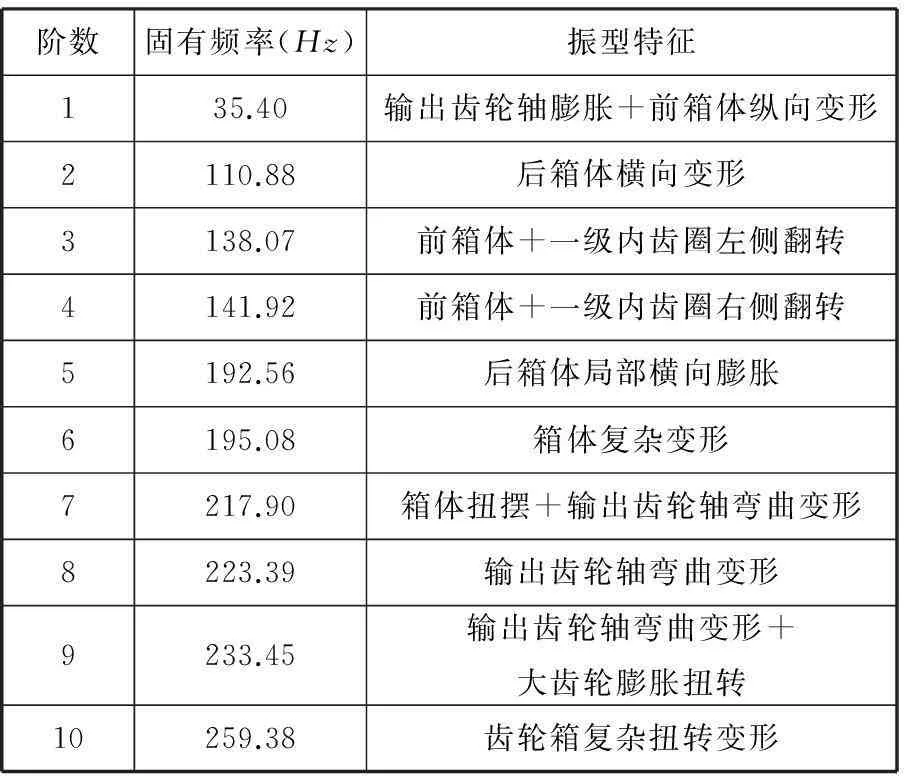
表2　风电齿轮箱前10阶固有频率及振型

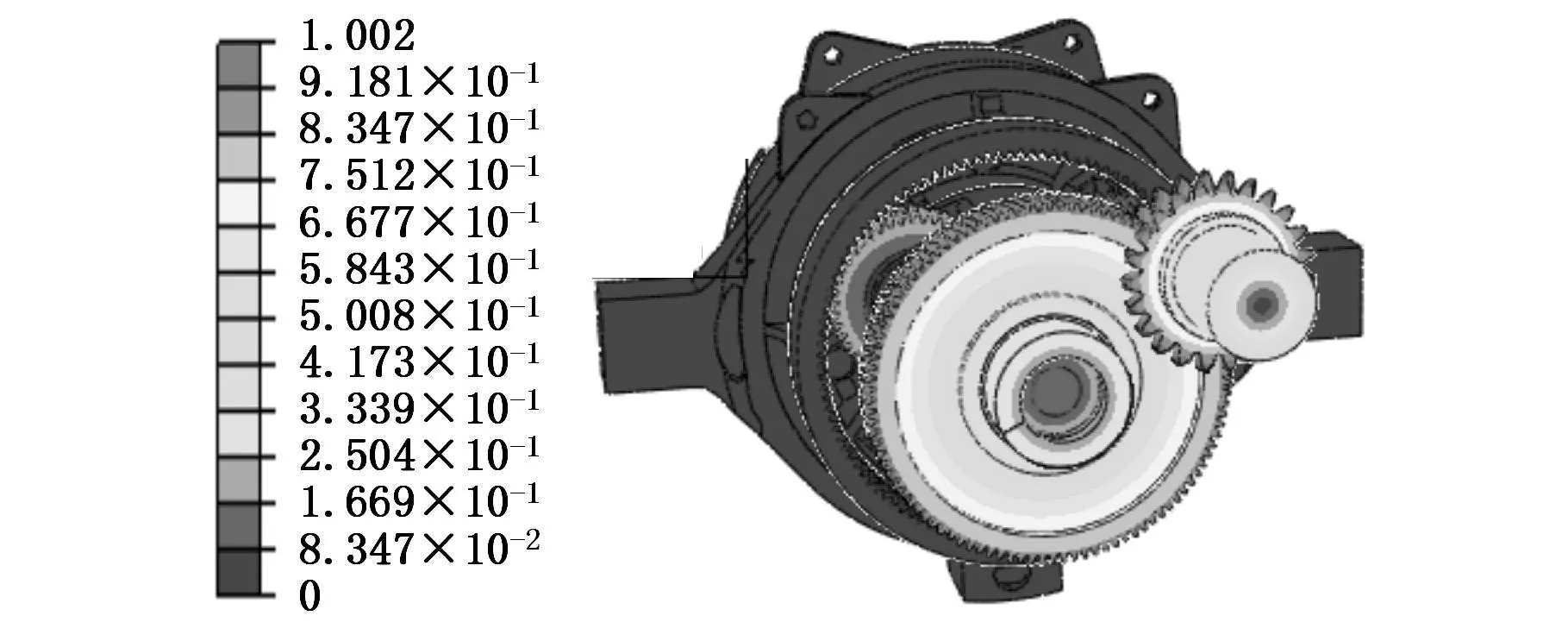
(a)第1阶振型

(b)第2阶振型图12　风电齿轮箱振型图

3.2风电齿轮箱系统动态响应分析

在ABAQUS软件中，基于模态计算结果，把动态激励施加到各级齿轮啮合位置上，采用振型叠加法对齿轮箱系统进行瞬态响应分析。把求解得到的各点位移、速度和加速度振动特性时域曲线，经过快速傅里叶变换(FFT)得到对应的频响曲线。为了保证求解精度，选取若干连续周期进行分析以消除瞬态激励产生的影响。在振动较大的轴承座处，布置齿轮箱测试点位置，如图13所示。

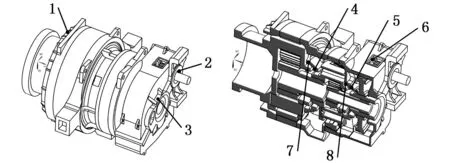
图13　齿轮箱测试点分布

对齿轮箱各测试位置在三个方向的振动响应曲线进行分析，以测试点3为例，结果如图14～图16所示。

(a)位移时域曲线(b)速度时域曲线

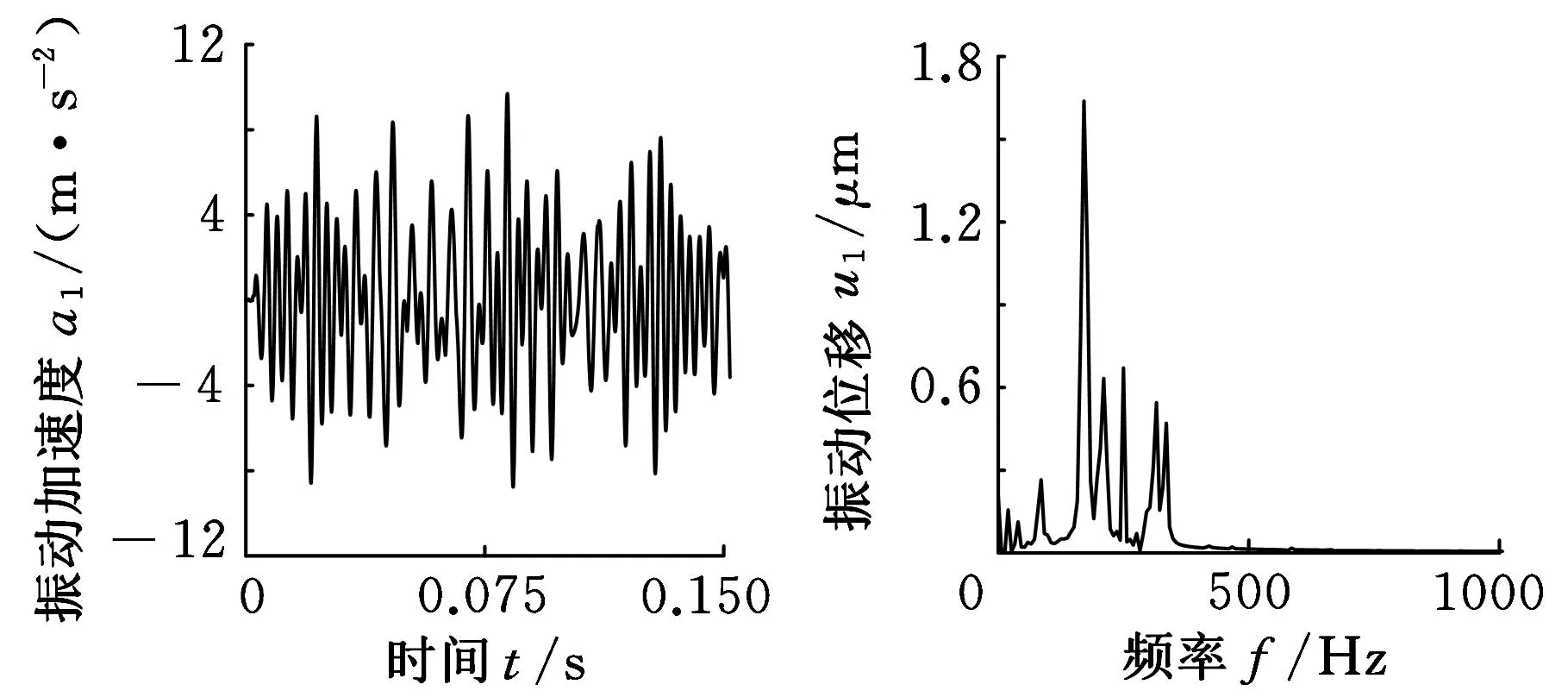
(c)加速度时域曲线(d)位移频域曲线图14　测试点3振动响应(X向)

(a)位移时域曲线(b)速度时域曲线

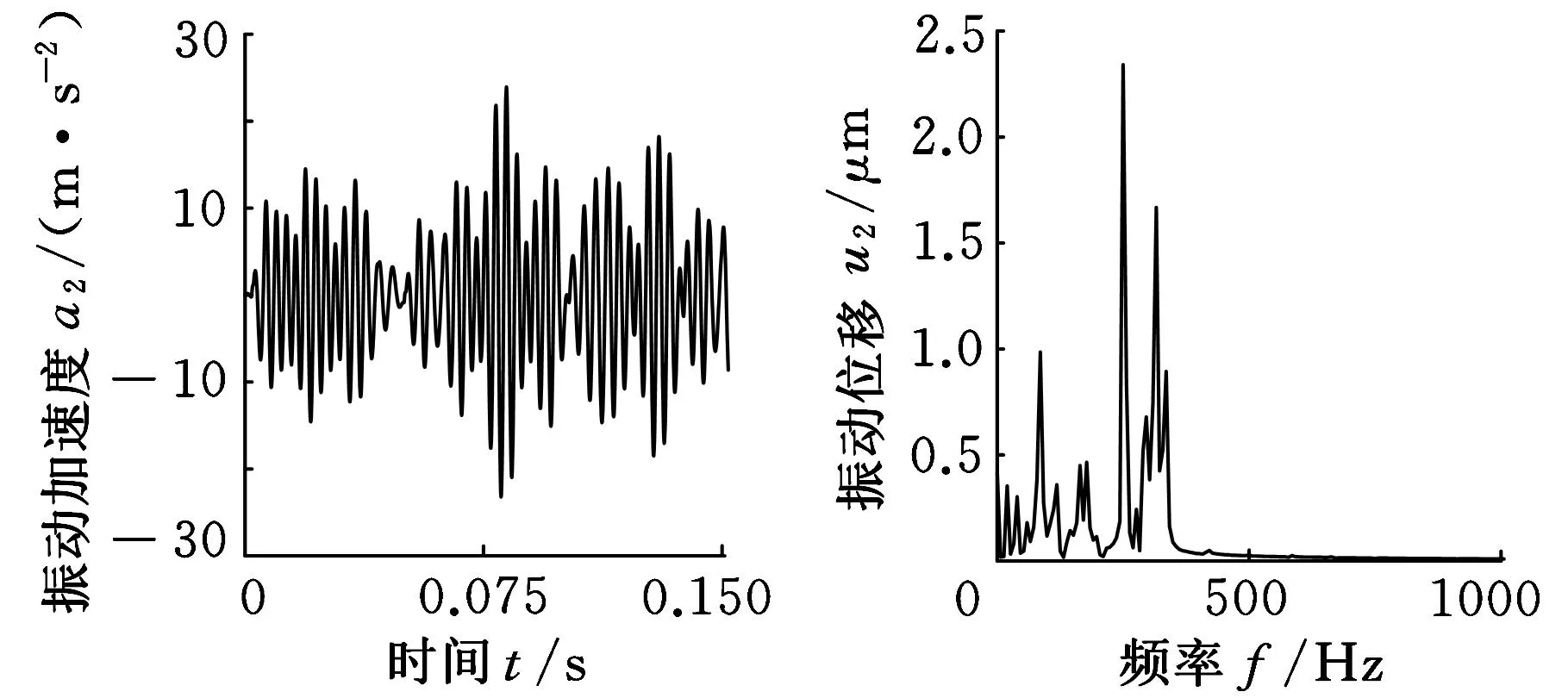
(c)加速度时域曲线(d)位移频域曲线图15　测试点3振动响应(Y向)

从X、Y、Z三方向的频谱图分析可知，测试点3位置处主要在400 Hz以下频率发生振动，第一级啮合频率和第二级啮合频率引起的振动比较显著，第三级啮合频率产生的振动比较小。

采用各测试点振动速度有效值来评价齿轮箱系统振动大小，反映齿轮箱振动的强烈程度。振动强烈程度由如下表达式定义：

(9)

(a)位移时域曲线(b)速度时域曲线

(c)加速度时域曲线(d)位移频域曲线图16　测试点3振动响应(Z向)

式中,vS为振动强烈程度,mm/s；vX、vY、vZ分别为X、Y、Z三方向上的振动速度有效值,mm/s；NX、NY、NZ分别为X、Y、Z三方向上的计算点数。

齿轮箱上各测试点位置在X、Y、Z三方向上计算得到的振动速度有效值如表3所示。

表3　各位置振动速度有效值　mm/s

由表3可知，各计算节点的振动速度有效值均小于4.5mm/s，根据GB/T6404.2-2005-T测定标准对齿轮箱振动进行评估，齿轮箱处于B级振动水平，处于正常振动状态。

结构噪声是在齿轮啮合过程中产生的，啮合过程中齿轮发生的冲击和摩擦导致振动噪声产生。在齿轮传动系统中，齿轮是主要的噪声源。结构噪声包括自鸣噪声和加速度噪声两部分，其中加速度噪声占主要部分，约占结构噪声的85%～90%[11]。对齿轮箱振动特性分析得到的加速度频响结果进行1/3倍频程转换就可以得到不同频率段的结构噪声值。以测试点3位置处的加速度噪声频率分布直方图为例，见图17。

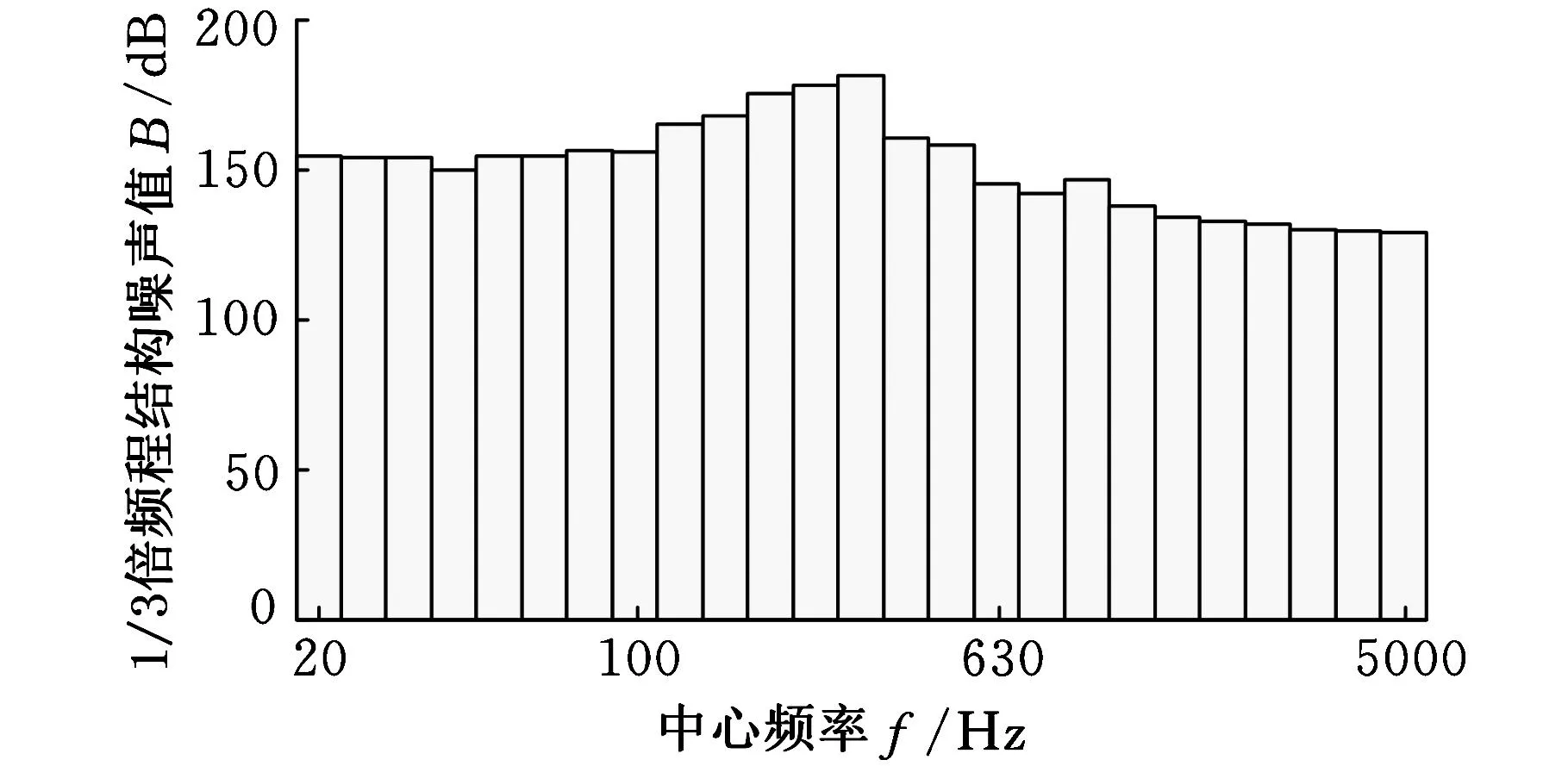
图17　测试点3加速度频率分布直方图

由图17可以看出，在第3级啮合频率附近处加速度噪声值达到最大值。

4结论

(1)对齿轮箱各级轮齿时变啮合刚度激励、误差激励以及啮入冲击激励进行模拟并合成内部动态激励，并将该内部动态激励作为求解齿轮箱振动响应的输入激励。

(2)采用Lanczos法对齿轮箱进行模态分析，前两级啮合频率不在固有频率附近，不产生共振现象，第3级啮合频率与第44级固有频率相近，但属于高阶共振，对结构影响较小。

(3)采用振型叠加法对齿轮箱进行振动响应分析得出，系统主要在400Hz以下频率发生振动，前两级啮合频率产生的振动比第3级啮合频率产生的振动大，不过齿轮箱振动处于正常范围。

(4)对测试点3位置处的结构噪声值进行分析得出，在第3级啮合频率附近处加速度噪声值达到最大值，结合振动实验可以优化测点布置，为大兆瓦级增速齿轮箱振动状态的在线监测奠定基础。

参考文献：

[1]AbboudiK，WalhaL,DrissY,etal.DynamicBehaviorofaTwo-StageGearTrainusedinaFixed-SpeedWindTurbine[J].MechanismandMachineTheory,2011,46:1888-1900.

[2]HelsenJ，VanhollevekeF,MarrantB,etal.MultibodyModelingofVaryingComplexityforModalBehaviorAnalysisofWindTurbineGear-Boxes[J].RenewableEnergy,2011,36: 3098-3113.

[3]KahramanA.AKinematicsandPowerFlowAnalysisMethodoloyforAutomaticTransmissionPlanetaryGearTrains[J].JounalofMechanicalDesign,2004,126: 1071-1081.

[4]马辉，朱丽莎，王奇斌，等.斜齿轮—平行轴转子系统模态耦合特性分析[J].中国电机工程学报，2012,32(29):131-136.

MaHui,ZhuLisha,WangQibin,etal.ModalCouplingCharacteristicAnalysisofaHelicalGearRotorSystemWithParallelShafts[J].ProceedingsoftheCSEE, 2012,32(29):131-136.

[5]AbbesMS,BouazizS.AnAcoustic-structuralInteractionModelingfortheEvaluationofaGearbox-radiatedNoise[J].MechanicalSciences,2008,50:569-577.

[6]陆波，朱才朝，宋朝省,等.大功率船用齿轮箱耦合非线性动态特性分析及噪声预估[J].振动与冲击，2009,28(4):76-80.

Lu Bo, Zhu Caichao, Song Chaosheng, et al. Coupled Nonlinear Dynamic Characteristics Analysis and Noise Pre-estimation of a Large Burden Marine Gearbox[J]. Journal of Vibration and Shock, 2009,28(4):76-80.

[7]魏静，孙清超，孙伟,等.大型风电齿轮箱系统耦合动态特性研究[J].振动与冲击，2012,31(8):16-23.

Wei Jing, Sun Qingchao,Sun Wei, et al. Dynamical Coupling Characteristics of a Large Wind Turbine Gearbox Transmission System[J]. Journal of Vibration and Shock, 2012,31(8):16-23.

[8]李润方，王建军.齿轮系统动力学-振动、冲击、噪声[M].北京：科学出版社，1997.

[9]李瑰贤，马亮，林少芬.宽斜齿轮副啮合刚度计算及扭振特性的研究[J].南京理工大学，2002,26(1):35-38.

Li Guixian,Ma Liang,Lin Shaofen. Research on Calculating Meshing Stiffness and Torsion Vibration Property of a Helical Geared System[J]. Journal of Nanjing University of Science and Technology, 2002,26(1):35-38.

[10]Lin Tengjiao, Ou H, Li Runfang.A Finite Element Method for 3D Static and Dynamic Contact/Impact Analysis of Gear Drives[J].Computer Method in Applied Mechanics and Engineering，2007,196(9/12):1716-1728.

[11]Guan Y H, Li M F, Lim T C, et al．Comparative Analysis of Actuator Concepts for Active Gear Pair Vibration Control[J]．Journal of Sound and Vibration， 2004，269(1/2)：273-294．

(编辑袁兴玲)

Analyses of Dynamic Coupling Characteristics and Structural Noise of Multi-Megawatt Wind Turbine Gearbox

Yang Changhui1Xu Taojin1Wu Canyuan2

1.Key Laboratory of Advanced Manufacturing Technology for Automobile Parts,Ministry of Education,Chongqing University of Technology,Chongqing,400054

2.Chongqing Gearbox Co.,Ltd.,Chongqing,402263

Abstract:Wind-turbine gearbox was one of the most important components of wind-turbine, its dynamic performance had direct impact on the whole system. A coupled nonlinear dynamic FE model containing gears-shafts-bearings-housing for a multi-megawatt wind turbine gearbox of planetary gear transmission was built comprehensively to perform the coupled modal analysis of the whole gearbox with Lanczos method. In consideration of the nonlinear factors of the time-varying mesh stiffness of spur and helical gears, gear errors and gear mesh impact, the dynamic response of the system was studied using direct integration method under the effects of internal excitation. The vibration displacement, velocity and acceleration as the dynamic evaluation indexes of the wind turbine gearbox were obtained, and the structural noise was also analyzed. All results provide useful theoretical basis for dynamic optimization of multi-megawatt wind turbine gearbox system.

Key words：wind turbine gearbox; internal excitation; dynamic response; structural noise

作者简介：杨长辉，男，1976年生。重庆理工大学机械工程学院副教授。主要研究方向为机械制造及其自动化。徐涛金，男，1991年生。重庆理工大学机械工程学院研究生。吴灿元，男，1987年生。重庆齿轮箱有限责任公司工程师。

中图分类号：TH12；TH122

DOI：10.3969/j.issn.1004-132X.2016.05.007

基金项目：国家科技支撑计划资助项目(2012BAA01B05)；国家国际科技合作专项项目(2013DFA70730)；重庆市教委科学技术研究资助项目(KJ1400938)

收稿日期：2015-03-23