行胜于言：命题研讨重在变式改编——以两道八年级期末几何综合题为例

☉江苏省东海县张湾中学　朱春水



行胜于言：命题研讨重在变式改编——以两道八年级期末几何综合题为例

☉江苏省东海县张湾中学朱春水

我们知道，七、八年级期末考试通常是地区（县、区）为单位组织命题，然而相比中考命题来看，由于研制团队、打磨时间等诸多因素的影响，不少考题仍然有打磨优化的空间，本文梳理两道考题的批阅手记、变式改编，最后再就命题研究提出一些初步思考，供研讨.

一、两道考题的批阅手记和变式改编

考题1：如图1，平面直角坐标系中，点A的坐标为（4，0），以OA为一边，在第四象限作等边△OAB，点C是y轴上一动点，连接AC，以AC为一边，在直线AC的下方作等边△ACD.

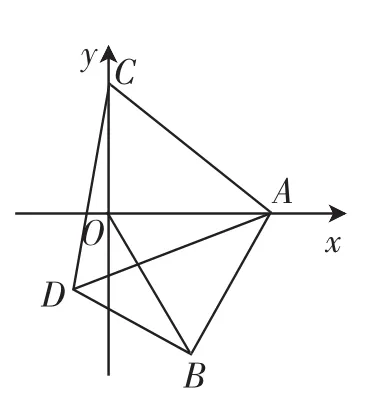
图1

（1）随着点C的运动，∠ABD的大小是否会发生变化？请说明理由.

（2）是否存在点C，使得△ABD是等腰三角形？若存在，求此时C点的坐标；若不存在，请说明理由.

批阅手记：笔者访谈学生解答情况表明，在20分钟内能完全贯通思路的不到10%，追问原因，发现不少优秀学生都是因为第一问中的线段繁多，没有能迅速捕捉、聚焦在△ACO和△ADB，从而影响了思考的方向，在外围转圈子，消耗时间；第二问能给出两解的更是少数，不少学生难以想象当点C在y轴负半轴上的图形，从而影响了思路获取.为了追求考题的易进难出，渐次生长，我们给出如下变式.

变式改编1：如图2，平面直角坐标系xOy中，点A的坐标为（4，0），以OA为一边作等边△OAB（顶点B在第一象限），点C是y轴负半轴上任意一点，连接AC，以AC为一边作等边△ACD.

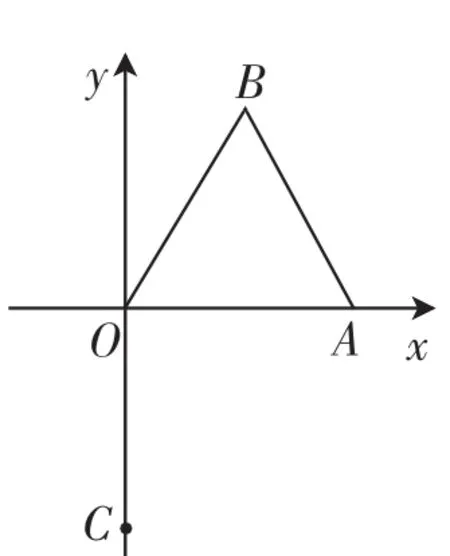
图2

（1）当点C的坐标为（0，-4）时，在图2中作出符合要求的△ACD.（要求：尺规作图，保留痕迹，不写作法）

（2）当点D落在第二象限时，连接BD，求证：AB⊥BD.

（3）设直线BD交x轴于点E，当OE=4时，求点C的坐标.

改编意图：为了使得题干信息所对应的图形比较简洁，我们把等边△ACD隐去，而安排学生在第一问中以尺规作图的方式自主画出，同时让学生注意要分类讨论，这事实上也是修正“考题1”中的不恰当表述“在直线AC的下方作等边△ACD”，在几何语句中，通常不可以描述直线上方、下方这样的个性化语句；第二问则是限制点D出现在第二象限后，让学生研究∠ABD的不变性；第三问则将问题放开，全面探究点C的可能位置，而又是关于两个特殊位置的研究，如果学生在第一问就漏解，则第三问也可能会漏解，但第一、三问之间又可以互相暗示、启发、呼应.

人文意境：一个“稳定”“向上”的等边三角形传递着正能量；那个不确定的等边三角形第3个顶点D，“上下呼应”，可不要忽视躲藏在“下面”的“D”呀，一旦解放C点在y轴负半轴的限制，很可能“谷底扎根，浴火重生”……

考题2：（2014年黑龙江齐齐哈尔，第26题改编）在△ABC中，AB=AC，∠BAC=90°，如图3，过点A作直线MN∥BC，D为直线MN上一点，连接BD，过点D作DE⊥BD，交AC于点P.

（1）求证：BD=DP.

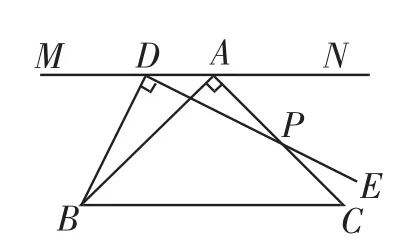
图3

图4

（2）如图4，若DE与CA的延长线交于点P，BD=DP是否成立？如果成立，请给予证明；如果不成立，请说明理由.

（3）在图5中，DE与AC的延长线交于点P，BD与DP是否相等？请直接写出你的结论，无需证明.

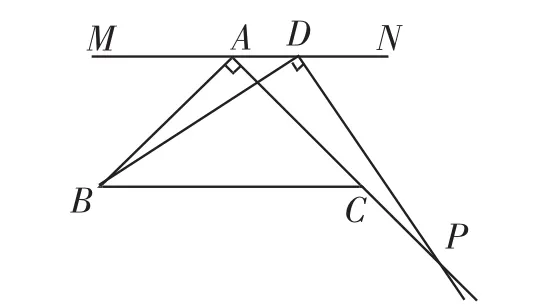
图5

批阅手记：这道考题改编自2014年黑龙江齐齐哈尔中考数学卷第26题，占8分，据说评分标准是前两问各3分，第三问2分.不少学困生什么都不会，只是在第二问中写了一个“成立”，第三问中写了一个“相等”，结果得3分；而不少优秀学生在第一问就消耗了大量精力，没有时间再解决第二、三问，也就什么都没有写，也得3分.批阅的老师们都感觉到极不公平、哭笑不得.可见这道考题的两个严重缺陷：第一，梯度不合理；第二，设问不恰当，导致评分不合理.以下给出变式改编.

变式改编2：在Rt△ABC中，∠BAC=90°，AB=AC，过点A作直线MN∥BC，D为直线MN上一点，连接BD，过点D作DE⊥BD，交直线AC于点P.

（1）如图3，当点P落在边AC上时，点D到直线AB、AC的距离_____相等；（填“一定”或“不一定”）

（2）如图4，若DE与CA的延长线交于点P，求证：BD= DP；

（3）当点D在射线AN上时，连接BP，判断△BDP的形状，并说明理由.

改编意图：虽然考题2的证明方法多样，辅助线构造也很多，然而能顺利揭示不同小问之间的关系的一种辅助线是过点D向AB、AC引垂线段，这样随着点D的变化，这种辅助线都可快速贯通思路，所以我们安排了第一问的填空，为的是启发学生；而第二问继续给出图形，但是要证明“BD=DP”，如果善于利用第一问中的启发就可顺利求证，如果另起炉灶，也有很多思路可以贯通；第三问则没有给出图形，要求学生自已画出符合要求的图形并证明，将能力提到一定高度，实现必要的区分功能，而不是让什么都不懂的学困生可以猜想“相等”就能拿到两分，就数学的本质来看，“猜想”虽然是重要的，可是离开“证明”还算是数学吗？

二、关于命题的进一步思考

1.命题工作责任重大，使命光荣，切忌原题照抄

从当前网络上流行的很多地区的期末试卷来看，大多数地区的把关题（这里主要是指全卷的最后一两题，用以承担对优秀学生的区分功能）仍然是简单的“拿来主义”或“低级改编”，甚至有不少地区是“原题照抄”，这种迎合题海战术的原题照抄或低级改编现象是需要批判的，其导向是鼓励本地区师生在复习备课时开展大量的练习、题海战术，“你做得多就能碰得到原题”的命题导向一定要在命题中得到回避，这也是让试卷公平、公正的基本保证.

2.命题工作需要修炼“三个理解”基本功

近年来，人民教育出版社中学数学室原主任章建跃博士提出的“三个理解”在教学研究、课例研究中得到普遍的重视和实践.然而在命题工作中，还鲜有研究者从基于理解数学、理解教学、理解学生的角度开展命题研究工作，笔者认为，“三个理解”恰恰也应该是命题工作的立足点，一道试题的呈现往往反映了命题者本身对数学的理解，是追求繁杂、冗长的数学问题呈现还是简洁大气、自然好懂的数学问题呈现，往往反映了命题者本身的旨趣品味和价值取向.此外，像“考题2”那样，上来第一问就是一个比较难的证明题，甚至把不少优秀学生都拒之门外的设问方式，显然是在“理解学生”这个角度上做得不够.章建跃博士也曾“非常肯定的”说过，“好的题目”绝不是教辅资料中汇编的各地的考题、练习，“好的题目”要追求易进难出，自然生长，简洁好懂，值得回味等.从这个意义上说，我们对两道考题的改编也是想倡导简洁自然、易进难出，吸引更多考生参与进来，同时也有效避免出现“考题2”评分上的尴尬处境.

参考文献：

1.罗增儒.数学解题学引论［M］.西安：陕西师范大学出版社，2008.

2.【美】波利亚，著.怎样解题［M］.阎育苏，译.北京：科学出版社，1982.

3.邓东皋，孙小礼，张祖贵，编.数学与文化［M］.北京：北京大学出版社，1999.

4.钟启泉.“批判性思维”及其教学［J］.全球教育展望，2002，31（1）.

5.刘东升.经历问题生成，深刻理解教材——人教八上“每日一题”的命题实践与思考［J］.中学数学（下），2014（4）.