基于相似特征点集的SIFT匹配改进算法

高　放，陆频频，王　旭

(辽宁工程技术大学 测绘与地理科学学院,辽宁 阜新 123000)



基于相似特征点集的SIFT匹配改进算法

高放，陆频频，王旭

(辽宁工程技术大学 测绘与地理科学学院,辽宁 阜新 123000)

摘要：当影像中存在相似或重复场景时，传统SIFT匹配算法存在匹配成功率低，目前改进的SIFT匹配算法计算量大。基于相似特征点集的SIFT匹配改进算法，依据相似性或重复场景的影像纹理特点，在SIFT特征点匹配过程中，通过设定阈值提取初始同名点，建立针对未成功匹配参考特征点的相似特征点集，利用已获取初始同名点建立仿射几何约束模型构建参考特征点的匹配约束窗口，在该窗口内利用特征点相对主方向及尺度约束，对特征相似点集进行匹配获得同名点，最后采用RANSAC算法剔除误匹配点。对比实验结果表明，在影像像对间存在较多相似性场景，同时存在较大尺度缩放、旋转变换、视角及模糊差异的情况下，文中算法在匹配成功率和计算复杂度上具有明显的优势。

关键词：SIFT;相似特征点集;几何约束;匹配;初始同名点

在基于特征的影像匹配技术中，尺度不变特征变换 (Scale Invariant Feature Transform,SIFT)算法由于对尺度缩放、旋转及弱仿射变换保持良好的不变性而受到广泛关注[1-3]。当影像中存在重复或相似场景时，以梯度方向向量距离作为相似性测度将会降低特征匹配的成功率[4-6]。因此SIFT算法近年来被广泛改进，通常包括：第一类方法是建立几何约束模型来对特征点进行约束匹配。如利用核线模型、同名直线模型或影像粗匹配模型对特征点进行几何约束匹配[7-8]。这种方法匹配成功率较高，但需预先获取一些约束模型的参数。第二类方法是以初始匹配点出发，通过构建几何约束模型来对剩余特征点进行匹配[9]。相对于第一类方法，第二类方法匹配成功率更高，但不足之处在于需要对剩余特征点进行遍历几何约束，故耗时较长。第三类方法是在局部描述子的基础上引入了全局向量，以此来增大重复相似场景特征之间的差异[10]。但该方法需对所有特征点进行全局计算，增加了算法的复杂度，同时也很难对影像尺度变换保持不变性。

针对上述方法中存在的问题，本文依据影像中重复或相似场景的纹理特点，在SIFT特征匹配阶段，提出一种基于特征相似点集的匹配方法。该方法有异于先建立几何约束模型再进行特征向量匹配策略，而是基于传统SIFT特征匹配方法同时建立同名点集和相似特征点集，利用同名点约束相似点集进行匹配，从而有效限定相似性场景的特征匹配搜索范围，避免了传统特征点二次约束匹配的遍历计算，大幅降低算法的复杂度，提高相似性场景同名点匹配成功率。

1算法

如图1所示为本文提出匹配算法流程图，首先在像对影像上提取特征点，利用最近次近邻方法基于阈值判断得到两组点集，对不符合阈值要求的特征点求取对应影像中前n个最近邻特征点，构成针对该特征点的相似特征点集。符合阈值要求的匹配点通过随机几何约束模型及RANSAC算法剔除误匹配点后构成初始同名点，利用初始同名点构建约束窗口模型、特征点相对主方向和尺度约束模型，利用上述多种约束模型对特征相似点集进行约束匹配，满足要求的点构成新同名点，采用RANSAC算法剔除误匹配点后，最终基于同名点集对待匹配影像进行纠正。

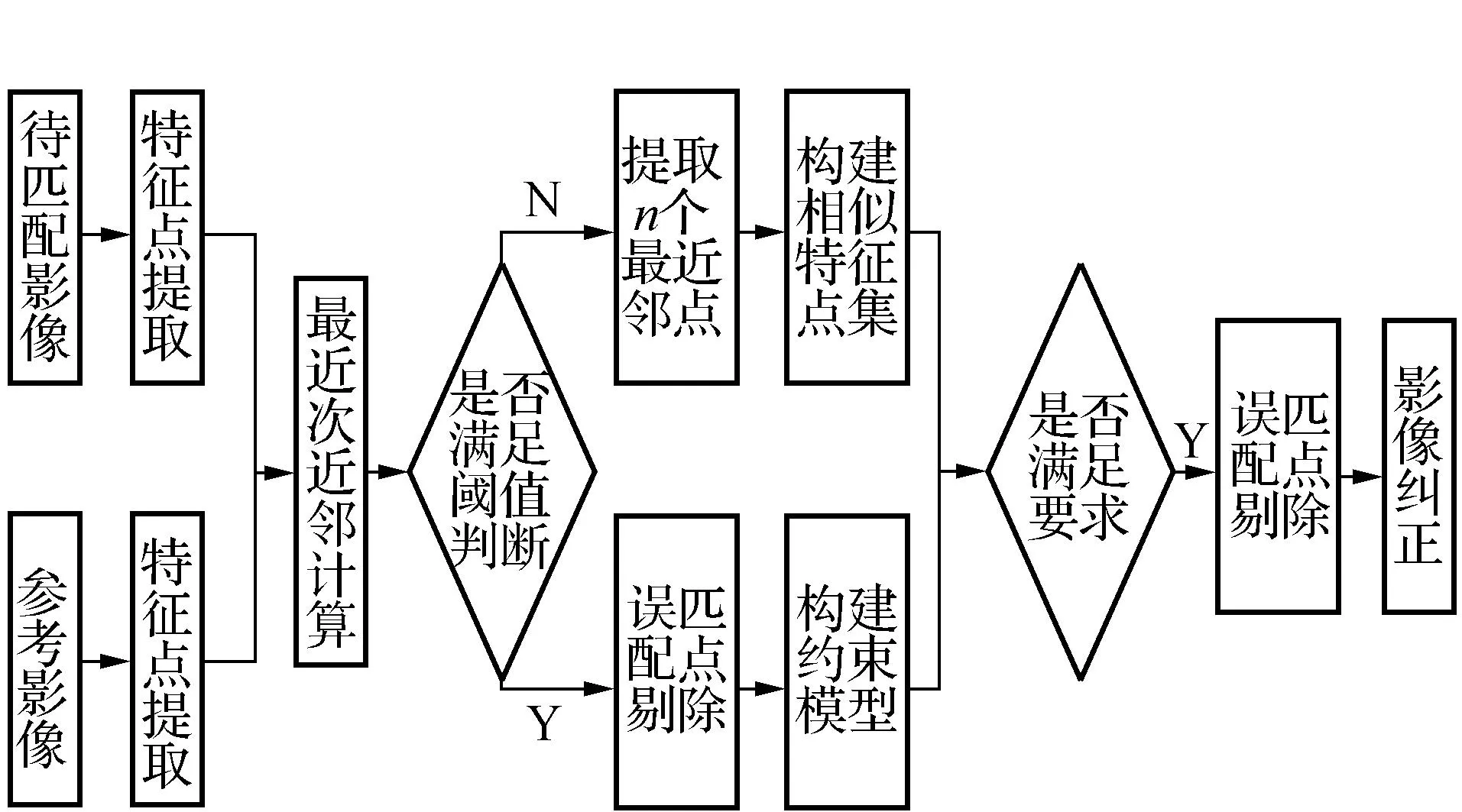
图1　匹配方法流程

1.1SIFT 算法简介

Lowe 在2004年总结前期工作的基础上，提出一种通过构建影像尺度空间的方式寻找对尺度、旋转、光照变换保持不变的兴趣点，并利用梯度方向向量来对特征点进行描述，其步骤包括：尺度空间构建、特征点主方向确定、描述符生成及特征匹配4个步骤。根据SIFT原理，特征点表达为

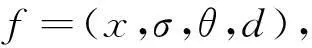
式中：x为特征点坐标，σ为平滑尺度因子，θ为特征点主方向，d为SIFT特征描述符。在SIFT算法中，匹配测度是通过计算特征点描述符之间的最近次近欧氏距离比值，低于最近次近距离阈值ε即为匹配点。

1.2初始匹配点提取与特征相似点集构建

当影像中存在重复或者相似场景时，传统SIFT匹配测度中阈值ε作用受到弱化，特征描述子之间的欧氏距离将出现以下情况：①真实同名点和相似特征点欧氏距离比值高于阈值ε；②相似特征得到的欧氏距离低于真实同名特征。其原因在于，SIFT特征描述子刻画的是特征点所在局部区域影像梯度方向向量信息。当不同特征点所在局部影像场景存在重复或者相似问题时，描述子趋于一致。依据相似性场景在影像中纹理信息近似的特点，假定欧氏距离最近邻中前n个特征点均可能成为潜在同名点，建立针对参考影像特征点对应的特征相似点集。

算法：

for (int i = 0；i < m；i++)

for(int k = 0；k < n；k++ )

{

if(di1/di2<ε)

(放入初始匹配点队列)break;

else

(将k点加入i点的相似特征点集)

}

其中，m为参考影像特征点数量，n为点i对应的待匹配影像上最近距离特征点数量。

1.3匹配测度

1)随机抽取3对匹配点，同时记录匹配点对之间的相对尺度和相对主方向平均值。两两判断相对尺度之差和相对主方向之差是否低于阈值h1，满足条件直接进入步骤(2)，否则重新随机抽取3对匹配点。

2)利用3对匹配点构建影像仿射变换模型，利用该模型求取参考影像上同名点在待匹配影像上的理论匹配点，当待匹配影像上理论匹配点与匹配点之间距离低于阈值h2时，保留该匹配点，否则该匹配点被剔除。

3)采用误匹配点剔除模型对步骤(2)处理后剩余的匹配点进行误差剔除，获得最终初始匹配点集。

利用初始匹配点集统计匹配点之间的平均相对尺度δσ和平均相对主方向δθ，对参考影像特征点及待匹配影像上的相似特征点集进行约束匹配。

首先利用初始匹配点采用最小二乘方法建立几何约束模型，通常遥感影像纠正模型包括透射模型、多项式模型，采用仿射变换模型作为几何约束模型：

(1)

式中：(X,Y)为待匹配影像点坐标；(x,y)为参考影像点坐标；a1，a2，a3，b1，b2,b3为变换系数。

如图2所示，利用式 (1) 计算的待匹配影像上理论匹配点，dr为约束窗口半径，窗口内黑点为对应在该窗口内相似特征点，箭头方向为特征点主方向。判断点PTref与窗口内相似特征点的相对主方向是否满足式(2)，符合要求方可作为候选匹配点。

(2)

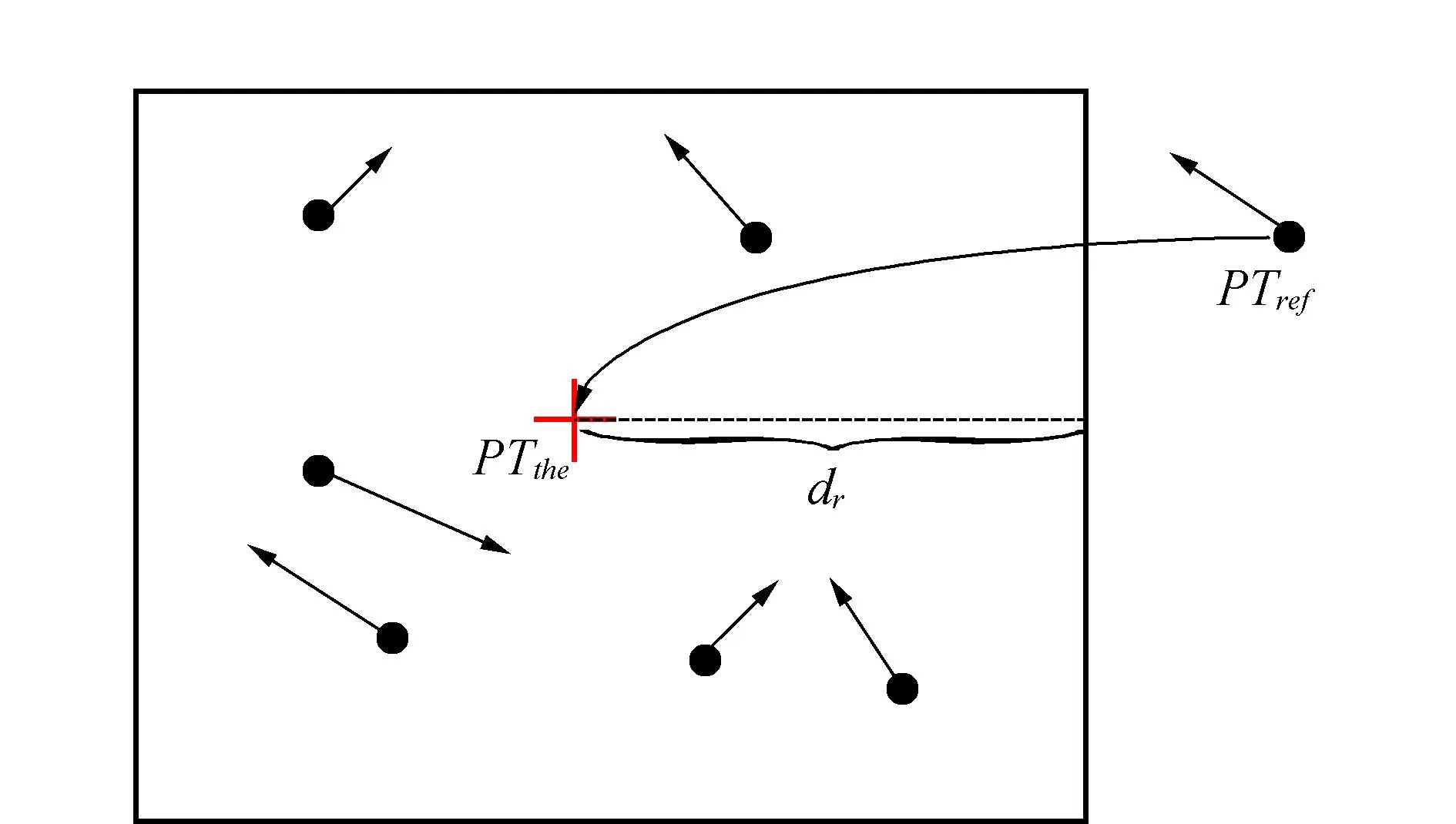
图2　约束窗口

通过式(3)判断点PTref与候选匹配点之间的相对尺度是否满足条件，满足条件候选匹配点可作为新同名点。

(3)

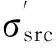
利用误匹配点剔除模型对新获取的同名点和初始同名点进行处理，得到最终的匹配点集。

1.4误匹配点剔除模型

初始匹配过程中均需要剔除低精度匹配点。通常误差剔除方法包括Data snooping方法和一致性检查方法[11-13]。但有关文献表明上述方法均受到初始匹配点分布影响，仅能剔除部分误匹配点。而随机抽样一致性算法 (Random Sample Consensus，RANSAC)采用随机抽样的方法，通过一种从局部到整体的策略实现误差的剔除[14]。该算法在样本中存在 50%以上的误匹配时，依然可以有效获取正确的匹配。因此，论文选取RANSAC方法剔除误匹配点。

2实验及其结果分析

2.1实验数据

选取不同类型含有较多相似性场景的影像像对进行实验，包括近景数字影像、航天卫星影像，同时像对间存在着尺度缩放、角度变形、影像模糊及视角变换等多种差异，以此来验证算法的稳健性。如图3所示4组测试数据中每行影像中按照从左到右顺序的第一幅为参考影像(即a1、b1、c1、d1)，第二幅为待匹配影像(即a2、b2、c2、d2)，相关数据描述见表1，由于所选取的影像类型不同，局部几何变形各异，无法采用如仿射、多项式、单应矩阵等全局性几何转换模型对影像进行纠正和检测匹配精度。在ENVI软件中利用人工来对影像均匀选取20对测试点，然后基于同名点利用小面元微分法对影像纠正计算测试点坐标，最后按照式(4)来计算匹配精度。

(4)

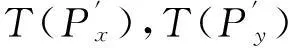
表1　测试数据描述

2.2实验结果与分析

如图3所示，由于同名点数量较大，尤其是c组数据同名点超过1 000对，无法采用连线方式清晰显示同名点结果，为了更好的显示纠正结果，将待匹配影像纠正结果与参考影像进行叠加分析。如图3所示，每行影像中按照从左到右顺序的第三幅为待匹配影像纠正后与参考影像的叠加结果，从图3中可以看到纠正影像与参考影像纹理吻合效果很好。

表2给出本文算法与经典SIFT算法匹配方法的比较分析结果。其中，表中匹配点表示剔除粗差后剩余的正确匹配点。

1)由表2可以看到，相对于其他两种方法，虽然在4组像对中本文方法计算速度居中，但对比同名点数量，本文算法具有明显的优势。这说明当影像存在相似或重复场景时SIFT算法的匹配成功率低问题，本文算法能够给予很好的解决。从影像匹配精度上来看，本文算法具有最高的精度。

图3　各组数据的匹配结果

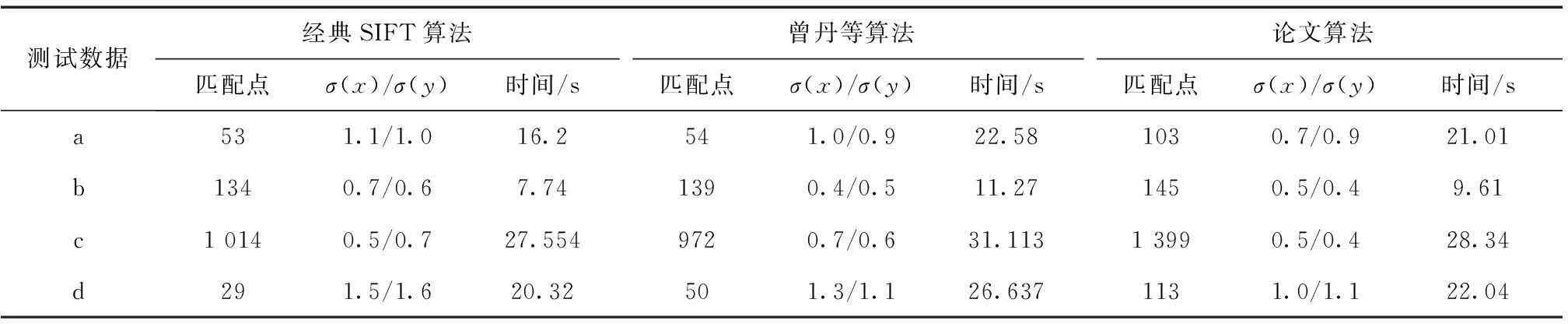
测试数据经典SIFT算法曾丹等算法论文算法匹配点σ(x)/σ(y)时间/s匹配点σ(x)/σ(y)时间/s匹配点σ(x)/σ(y)时间/sa531.1/1.016.2541.0/0.922.581030.7/0.921.01b1340.7/0.67.741390.4/0.511.271450.5/0.49.61c10140.5/0.727.5549720.7/0.631.11313990.5/0.428.34d291.5/1.620.32501.3/1.126.6371131.0/1.122.04

2)在数据(a)组和数据(d)组可以看到，影像间均存在较大的尺度缩放和角度变形问题，尤其(a)组像对间存在接近于3倍尺度缩放。通过对3种算法的同名点数量与影像匹配精度对比分析表明，本文算法的匹配点数量是其他两种算法的2倍，同时精度更高，表明本文算法能够满足较大尺度缩放和旋转变换下的影像匹配问题的需求；而对像对间存在接近于135°角度变形的数据(d)组分析表明，当影像中存在相似性场景的梯田特征数量较大，采用梯度方向向量作为匹配测度的SIFT匹配方法数量明显较低。而本文算法由于利用场景间的特征相似性建立相似点集，并通过特征几何约束、相对主方向及尺度等多重约束，避免了特征向量之间的二次匹配，因而能够提高算法匹配的速度，并较好解决了相似性场景的匹配问题。

3)针对模糊影像的匹配问题，本文选取了数据(b)组的数据来进行验证分析。由于数据(b)组影像间存在模糊现象，使得不同特征场景纹理特征之间相似性加大，相异性降低，这为不同场景特征的独特性描述带来困难，从而降低SIFT算法匹配的成功率。本文算法和曾丹等算法在匹配数量和精度上相差不大，均比SIFT算法有所提高，而相对于曾丹等算法，本文算法的计算速度更高。

4)如图3(c)所示，针对视角变化问题，本文选取的是纹理相似度极大且视角存在较大差异的墙面。本文算法的匹配成功率和精度均为最高，表明本文算法良好的匹配性能。

3结论

SIFT特征描述子作为一种局部描述子，当影像中存在相似性大或重复的场景时传统匹配算法成功率低，而目前改进的SIFT匹配算法也存在计算量大的问题。有鉴于此，本文依据相似性场景的纹理特点，提出一种基于相似特征点集的SIFT匹配改进算法。当影像间存在相似性场景及不同几何变形差异情况下，与其他算子的实验比较表明，本文算法具有计算量小、匹配点数量大、匹配精度高的优点。但由于在算法设计过程中需要人为分析设定一些参数，因此如何进一步改进算法实现参数的自动化设定将是未来研究的方向。

参考文献：

[1]郭俊喜.多源高分辨率遥感影像自动匹配算法[J].测绘工程，2014,23(7)：17-21.

[2]王亚东,雷国华,安波,等.一种仿人足球机器人视觉系统环境特征获取与识别方法[J].黑龙江工程学院学报(自然科学版),2013,27(2)：68-71.

[3]曾丹,史浩,张琦.多相似内容图像的特征匹配[J].计算机辅助设计与图形学学报, 2011,23(10):1725-1733.

[4]袁修孝,李然.带匹配支持度的多源遥感影像SIFT匹配方法[J].武汉大学学报(信息科学版),2012,37(12):1438-1442.

[5]史建东，耿利川，秦永志.基于BSIFT的无人机影像快速拼接算法[J].测绘与空间地理信息，2015，38(5)：124-127

[6]李鹏,武文波,王宗伟,基于非线性尺度空间的多源遥感影像匹配[J].测绘科学，2015，40(7)：41-45.

[7]戴激光,宋伟东,贾永红,等.一种新的异源高分辨率光学卫星遥感影像自动匹配算法[J].测绘学报,2013,42(1):80-86.

[8]康永辉,戴激光,宋伟东.异源高分辨率遥感影像的三维重建[J].测绘科学，2015，40(6)：156-161.

[9]WU B,ZHANG Y,ZHU Q.A triangulation-based hierarchical image matching method for wide-baseline images[J].Photogrammetric Engineering & Remote Sensing,2011,77(7)：695-708.

[10] 纪华，吴元昊，孙宏海，等.结合几何全局信息的SIFT特征匹配算法[J].光学精密工程,2009,17(2):439-444.

[11] 王恺,陈世平,曾湧,一种遥感影像同名点密集匹配方法[J].测绘科学，2015，40(4)：141-146.

[12] 张登荣,蔡志刚,俞乐.基于匹配的遥感影像自动纠正方法研究[J].浙江大学学报(工学版),2007,41(3):402-406.

[13] 张海荣,刘燕华,孙久运.航空影像自动化镶嵌及几何纠正[J].测绘科学，2015，40(8)：72-76.

[14] 侯天怡,尤红建,孙显.以卫星影像为底图的无人机图像自动拼接方法[J].测绘科学，2015，40(6)：11-16.

[责任编辑：李铭娜]

Improved sift matching algorithm based on similar feature point setGAO Fang,LU Pinpin,WANG Xu

(School of Geomatics,Liaoning Technical University,Fuxin 123000,China)

Abstract：Considering the low matching rate of traditional SIFT algorithm and large amount of calculation for the present improved SIFT matching method when similar or repeat scene existing in images,a new improved SIFT matching method is proposed based on similar feature point set in this paper.Firstly,initial matching points are extracted by threshold during traditional SIFT mateching method,at the same time the similar feature point set is built for the reference point feature which can not be matched.Secondly,geometrical constraint model is constructed by the initial homonymy points,which is used to build constraint window for reference point feature.Then the relative scale and main orientation of SIFT features are utilized to extract the homonymy points.At last,RANSAC is imbedded to eliminate mismatching points.Compared with other matching algorithms,the proposed algorithm has significant advantages in terms of successful matching rate and computational complexity.

Key words：SIFT(scale inveriant feature transform);similar feature point set;geometrical constraint;matching;initial homonymy point

中图分类号：P216

文献标识码：A

文章编号：1006-7949(2016)06-0019-05

作者简介：高放(1992-)，女，硕士研究生.

收稿日期：2015-01-15;修回日期：2015-08-29