基于部分最小二乘岭估计的粗差定值定位

金丽宏，吕玉婷，汪　耀，许运鹏，张小龙

(1.武汉科技大学 城市学院，湖北 武汉 430083； 2.中国地质大学 信息工程学院，湖北 武汉 430074; 3.国家知识产权局专利局专利审查协作四川中心，四川 成都 610213; 4.中建二局第二建筑工程有限公司第四分公司，河南 郑州 450000)



基于部分最小二乘岭估计的粗差定值定位

金丽宏1，吕玉婷2，3，汪耀2，许运鹏2，张小龙4

(1.武汉科技大学 城市学院，湖北 武汉 430083； 2.中国地质大学 信息工程学院，湖北 武汉 430074; 3.国家知识产权局专利局专利审查协作四川中心，四川 成都 610213; 4.中建二局第二建筑工程有限公司第四分公司，河南 郑州 450000)

摘要：在利用部分最小二乘原理进行粗差定值定位时，模型的法方程矩阵可能存在病态性，使得到的粗差定值定位结果不可靠。文中针对观测数据包含多个粗差且法方程病态问题，利用岭估计处理病态问题，建立部分最小二乘岭估计的粗差定值定位方法，给出粗差搜索步骤，利用迭代算法实现多个粗差的定值和定位。通过模拟算例分析部分最小二乘法、部分最小二乘岭估计在粗差搜索方面的效果，从另一个角度探讨粗差处理方法，推广现有的误差理论，证明文中方法的有效性。

关键词：粗差；病态性；部分最小二乘；岭估计；定值定位

在测绘数据处理中，粗差的存在严重影响最小二乘平差结果，为消除或减弱这种影响，国内外学者已进行广泛研究并得到不少解决粗差问题的方法，如数据探测法[1]、部分最小二乘法[2-4]、均值漂移法[5]、LEGE法[6-8]、拟准检定法[9]、抗差估计[10-11]等。部分最小二乘法原理简单，适用于处理数据量较大的观测值，文献[2]分别研究了观测数据独立或相关时粗差的定值定位方法，文献[3]研究了对相关观测值中粗差的快速搜索法。在实际测量中，因观测数据不足或平差模型中参数之间存在近似相关性，使得观测方程的系数矩阵表现出明显的复共线性，法方程矩阵出现病态问题。若观测数据同时存在病态性与粗差问题，因病态性的影响，部分最小二乘法对粗差定值定位失效。

为实现法方程矩阵病态的观测数据中多个粗差的定值定位，本文将岭估计[12-14]方法引入平差模型，建立了基于部分最小二乘岭估计的粗差定值定位理论。首先将观测值进行分组，利用岭估计处理病态问题，得到了该模型下的部分最小二乘岭估计及粗差估计值表达式；然后给出了逐次逐个粗差搜索的步骤，实现了多个粗差的定位。最后用一组算例验证了本文方法的有效性。该估计方法为处理同时存在粗差与病态的观测数据提供了一种新的思路，扩大了部分最小二乘法的适用范围。

1粗差定值

为实现观测数据中粗差的定值定位，基于系统聚类思想，将观测值分为两组，第1组为不含粗差的r个观测值Lr，第2组为含全部粗差的q个观测值Lq，则两组观测值基于Gauss-Markov平差模型的误差方程表示为

(1)

(2)

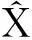
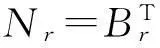
为克服病态性的影响，重新实现粗差的定值定位，将岭估计引进平差模型，根据岭估计的定义，则第1组观测值的平差准则为

(3)

其中：κ为岭参数，M为对称正定矩阵，对于岭估计，M通常为单位阵，观测式(1)在式(3)条件下得到的估计值即为部分最小二乘岭估计。

首先对于式(3)关于X求极小值，即有

(4)

再将式(1)代入式(4)得到参数解为

(5)

根据式(1)、式(5)得到第1组观测数据的残差为

(6)

相应的单位权中误差估值为

(7)

最后将式(5)代入式(2)得第2组观测值的改正数为

(8)

2粗差定位

实际测量中，粗差的个数与位置事先是无法得知的，通过逐步搜索每次定位一个粗差，直到找到全部粗差为止。观测值不含误差时其单位权中误差明显小于含粗差时的单位权中误差，因此，搜索过程中，通过判断最小二乘岭估计中最小的单位权中误差减小的程度决定是否继续搜索。结合文献[2]的判别标准与部分最小二乘岭估计，本文采用下式对单位权中误差减小的显著性进行判断。

(9)

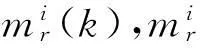
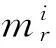
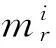
若bizhi>2，单位权中误差显著变小，说明观测数据中只含一个粗差，该单位权中误差所对应的观测值在原观测数据中的位置即为粗差位置q1，结束搜索；

若bizhi<2，单位权中误差有所减小但并不明显，表示观测值至少含2个粗差，需要继续进行搜索，进入步骤3)。

最后根据定位结果将观测值分为含粗差与不含粗差两组，对第1组观测值重新平差求得部分最小二乘岭估计，再根据式(8)算得粗差估值。

3算例分析

为了验证方法的有效性，现模拟一个算例进行证明。观测值为：L=BX+Δ，Δ～N(0,1)，观测值数n=10，X的真值为X=[11111]T，必要观测数t=5，其设计矩阵为

不妨在第2、6个观测值处分别加入大小为10的粗差。

根据病态性诊断方法中的条件数法[13]，计算法方程系数阵N=BTPB的条件数为1.289 2×105，病态性严重。

1)利用部分最小二乘法探测粗差。粗差搜索过程中，假设观测数据不含粗差时，平差求得的单位权中误差为1.686 6；假设观测值含一个粗差时，计算得到单位权中误差最小值为0.832 3，位置为第2个观测值，计算单位权中误差比值大于2，搜索结束，判断原观测值只有第2个观测值含粗差，与真实粗差位置不符。基于此定位结果算得的参数解为

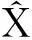
-118.402 43.989 9]T，

其值远远偏离真值。

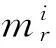
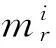
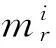
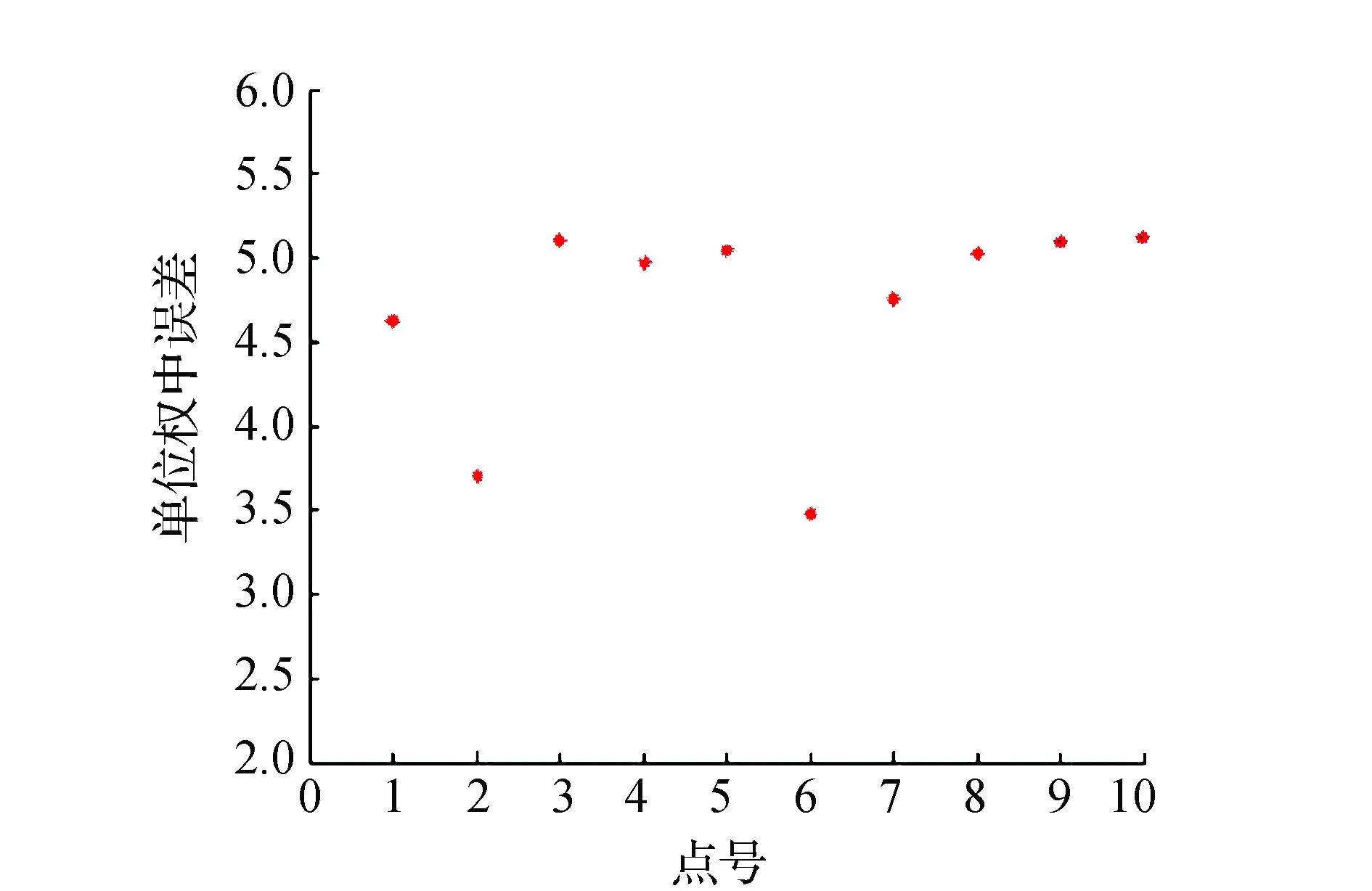
图1　假设有1个粗差时的单位权中误差

图2　假设有2个粗差时的单位权中误差

计算结果表明，当观测数据的法方程矩阵病态时，传统的部分最小二乘法对粗差定值定位失败；部分最小二乘岭估计方法可以在观测数据存在病态问题时实现多个粗差的定值定位。

4结论

对法方程矩阵病态的观测数据进行粗差探测，本文结合岭估计与部分最小二乘法各自的优点，提出了基于部分最小二乘岭估计的粗差探测方法，在改善数据病态性的同时，实现粗差的定值定位。通过公式推导与算例分析，可以得到如下结论：

1)当观测数据同时存在粗差与病态问题时，因病态性的影响，传统的部分最小二乘法无法对粗差定值定位。本文通过引入岭估计解决病态问题，并结合部分最小二乘原理推导出了部分最小二乘岭估计。

2)基于部分最小二乘岭估计得到了粗差估值表达式，通过逐次逐个搜索方法实现对多个粗差定位。利用模拟算例证明该方法能对多个粗差进行准确定位，且得到的粗差估值接近其真实值。

3)本文方法丰富了部分最小二乘理论，扩大了其适用范围，为处理包含粗差与病态问题的观测数据提供了一种思路。

参考文献：

[1]BAARDA W. A Test Procedure for Use in Geodetic Networks [J]. Netherlands Geod Comm.,1968,2(5):5-7.

[2]王爱生，欧吉坤.部分最小二乘平差方法及在粗差定值与定位中的应用[J].测绘科学，2005，30(2):70-72.

[3]林国庆，范东明，谢用.部分最小二乘平差的快速多维粗差定位定值法[J].测绘，2010，33(4):162-164.

[4]王海涛,欧吉坤,袁运斌，等. 估计观测值粗差三种方法的等价性讨论[J]. 武汉大学学报(信息科学版)，2013,38(2):162-166.

[5]宋力杰. 均值平移模型的理论研究及其分析[J].测绘学院学报，2009，17(3):160-162.

[6]於宗俦，李明峰. 多维粗差的同时定位与定值[J].武汉测绘科技大学学报，1996，21(4):323-329.

[7]於宗俦，李明峰. 对LEGE法性质的进一步讨论及其改进搜索方法[J].武汉测绘科技大学学报，1998，23(3):238-243.

[8]宋力杰，杨元喜. 均值漂移模型粗差探测法与LEGE法的比较[J].测绘学报，1999，28(4):295-300.

[9]欧吉坤. 粗差的拟准检定方法(QUAD法) [J]. 测绘学报，1999，28(1):15-20.

[10] 余学祥，吕伟才.抗差估计在粗差探测及平差计算中的应用[J].测绘工程，1996，5(3):40-44.

[11] 何伟，李明，阚起源.抗差加权非等时距GM(1，1)模型在大型建筑物沉降预测中的应用[J].测绘工程，2014，23(4):62-68.

[12] 归庆明，李国重. 岭-压缩组合估计及其在测量平差中的应用[J].大地测量与地球动力学，2002，22(1):16-21.

[13] 王振杰. 大地测量中不适定问题的正则化解法研究[D].中国科学院研究生院(测量与地球物理研究所)，2003.

[14] 丁士俊. 测量数据的建模与半参数估计[D]. 武汉：武汉大学，2005.

[责任编辑：刘文霞]

Location and evaluation of gross error based on partly least square ridge estimationJIN Lihong1, LYU Yuting2,3, WANG Yao2, XU Yunpeng2, ZHANG Xiaolong4

(1.City College,Wuhan University of Science and Technology,Wuhan 430083,China；2.School of Information Engineering, China University of Geosciences, Wuhan 430074,China;3.Patent Examination Cooperation Center of the Patent Office, SIPO, Chengdu 610213,China;4.The Fourth Construction Engineering Co.,Ltd. of China Construction Second Engineering Bureau, Zhengzhou 450000,China)

Abstract：By using the principle of partly least square to locate and value the gross errors in the observational data, the matrix equation of the adjustment model may have ill-posed problems, which results in the locations and evaluations of the gross error unreliable. For the observational data which contain gross errors and have ill-posed problems,firstly,this paper chooses the ridge estimation to deal with the ill-posed problems,then proposes a method based on the partly least square ridge estimation to locate and value the gross errors, and the specific search steps for gross errors are given. The locations and evaluations of the gross error can be gotten through the iterative algorithm. At last, the method of partly least square and the partly least square ridge estimation to locate and value the gross errors in one simulating computation are analyzed. The proposed method’s validity is verified. This method discusses the gross error approach from another perspective, which will extend the existing error theory.

Key words：gross error;ill-posed problem;partly least square;ridge estimation;location and evaluation

中图分类号：P207

文献标识码：A

文章编号：1006-7949(2016)06-0061-04

作者简介：金丽宏(1977-)，女，副教授.

基金项目：国家自然科学基金资助项目(41374017)

收稿日期：2015-03-25