一种基于K-D树优化的ICP三维点云配准方法
刘 江,张 旭,朱继文
(1.黑龙江工程学院 测绘工程学院,黑龙江 哈尔滨 150050;2.北京建筑大学 测绘与城市空间信息学院,北京 100044)
一种基于K-D树优化的ICP三维点云配准方法
刘江1,张旭2,朱继文1
(1.黑龙江工程学院 测绘工程学院,黑龙江 哈尔滨 150050;2.北京建筑大学 测绘与城市空间信息学院,北京 100044)
摘要:为提高三维点云数据配准精度和速度,提出一种基于K-D树优化的ICP三维点云配准方法,首先采用中心重合法实现点云数据的粗配准,然后利用K-D tree快速搜索最近点对改进传统ICP方法,完成三维点云数据精配准,该方法克服传统ICP算法中由于利用欧式距离来判断最近点所引起的工作量大、耗费时间多的缺陷,提高点云的配准速度。在此基础上利用斯坦福不同密度Bunny点云数据进行实验验证,结果表明在采用中心重合法实现三维点云粗配准的基础上,利用K-D tree优化ICP算法,能够提高点云配准的精度、速度和稳定性。
关键词:点云配准;k-d tree;中心重合;精度;稳定性
随着数字城市不断向前发展,大规模三维数据采集技术迅速提升,由激光原理、摄影测量原理等方式产生多种点云数据。这些三维点云数据不仅可以记录物体的空间信息,同时还可以得到物体表面的几何信息。在实际获取点云数据时考虑到测量设备、测量范围的限制以及被测物体外形的复杂性等,每次扫描只能获取当前视点下的点云,其坐标是相对于当前的仪器坐标系而言的,要得到被测物体完整的三维模型,需要从不同的视点对被测物体进行扫描,并将不同视点获取的点云数据进行配准。
H.Alt等提出基于Hausdorff距离和Frechetl距离几何结构形状的配准[1]。其中,在解决噪声点和局部遮挡等问题上Hausdorff距离体现出明显的优势,同时Hausdorff距离解决在计算变形时欧式距离所产生的扭曲与失真[2]。Frechetl距离是基于收敛性提出的,因此配准后的点云数据具有很强的收敛特性。Barequet等提出以有向脚标对部分表面进行配准,用这种方法进行配准既简单而又快速,但是不足之处是配准结果的精确度不高[3]。这些算法彼此之间存在着一定的共性,都是根据点云或曲面寻找特征相似的区域,寻求最佳的目标函数,利用目标函数值最小化来提高配准的精度。ICP算法最初由Besl和Mckey提出,是一种点配准方法,但配准的效率不高、耗费时间长,需要对算法进行一定的改进。在本文应用k-d tree的方法对ICP算法进行改进,进一步提高点云的配准效率。
1改进的三维点云配准算法
点云配准大致分成两个过程粗配准和精配准,粗配准是对点云数据的重叠部分进行大致拟合,为精配准提供平移和旋转参数的初始值,精配准是在粗配准的基础上进行再次配准,使用这种配准方式可以提高配准的准确度。目前,粗配准的方法主要有标签法、主方向贴合法、中心重合法等,在本文利用中心重合法进行点云粗配准。
1.1中心重合法
中心重合法在点云粗配准中利用点云A与待配准点云B的中心重合,从而降低两组点云数据之间的平移差值。
1)计算点云A与点云B对应点集的质心
(1)
(2)


(3)
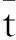
(4)
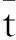
对两组点云数据进行中心重合,可缩小点云之间的平移错位,为下一步的精配准提供初始位置,提高点云的配准精度。
1.2精配准
在三维点云数据配准过程中,计算旋转变换矩阵和平移矩阵,这是任何一种算法都不可避免的。在利用粗配准得到的初始位置,本文选用ICP算法进行点云精配准,并在算法中用单位四元数算法求解迭代过程中的旋转矩阵。
1.2.1单位四元数算法
1)求解两组对应点集协方差
(5)
式中:∑ab两点集协方差;N为点云数目;
2)计算出反对称矩阵

(6)
式中:∑ba为∑ab的转置据矩阵。
3)利用求得的反对称矩阵A中A23,A31,A12位置上的元素定义一个新的列向量,Δ=[A23,A31A12]′.
4)用列向量Δ与上面的协方差∑ab组成一个新的4阶矩阵
(7)
式中:E3为一个三阶的单位矩阵;Δ′为Δ的转置矩阵;tr(∑ab)为协方差∑ab的迹。

(8)
式中:q0,q1,q2,q3为四元向量的参数;
(9)
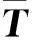
1.2.2ICP算法
ICP算法在点云配准中广泛应用,特别是在精配准过程中,在点云配准中进行迭代运算,配准精度高、效果可靠。ICP算法步骤:
1)确定对应点对:由点云A中的点在待配准点云B中搜索出相应的最近的点,组成对应点对。
2)计算两组新点集的质心,按照式(1)和式(2)计算新点集质心。
3)计算目标函数f(Rk,Tk),以目标函数值最小为原则。
(10)
式中:Rk为最优旋转矩阵;Tk为平移矩阵;f(Rk,Tk)为目标函数值。
4)用最优旋转矩阵Rk和平移矩阵Tk,使配准点云B坐标变换到Bk+1。
(11)
5)计算点对的平均距离
(12)
(13)
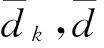
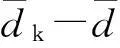
1.3ICP算法改进
ICP算法虽然在配准中广泛应用,但算法本身配准的效率低、花费时间长,特别在海量的点云数据中更为明显。因此需要对ICP算法进行改进,以提高配准的效率。传统的ICP算法以欧式距离为衡量标准来判断最近点,这种方式工作量大、耗费时间多。而利用K-Dtree能快速搜索最近点对,提高点云的配准效率。
图1为ICP算法配准流程,在寻找最近点对时,利用K-Dtree搜索最近点。其搜索步骤如下:
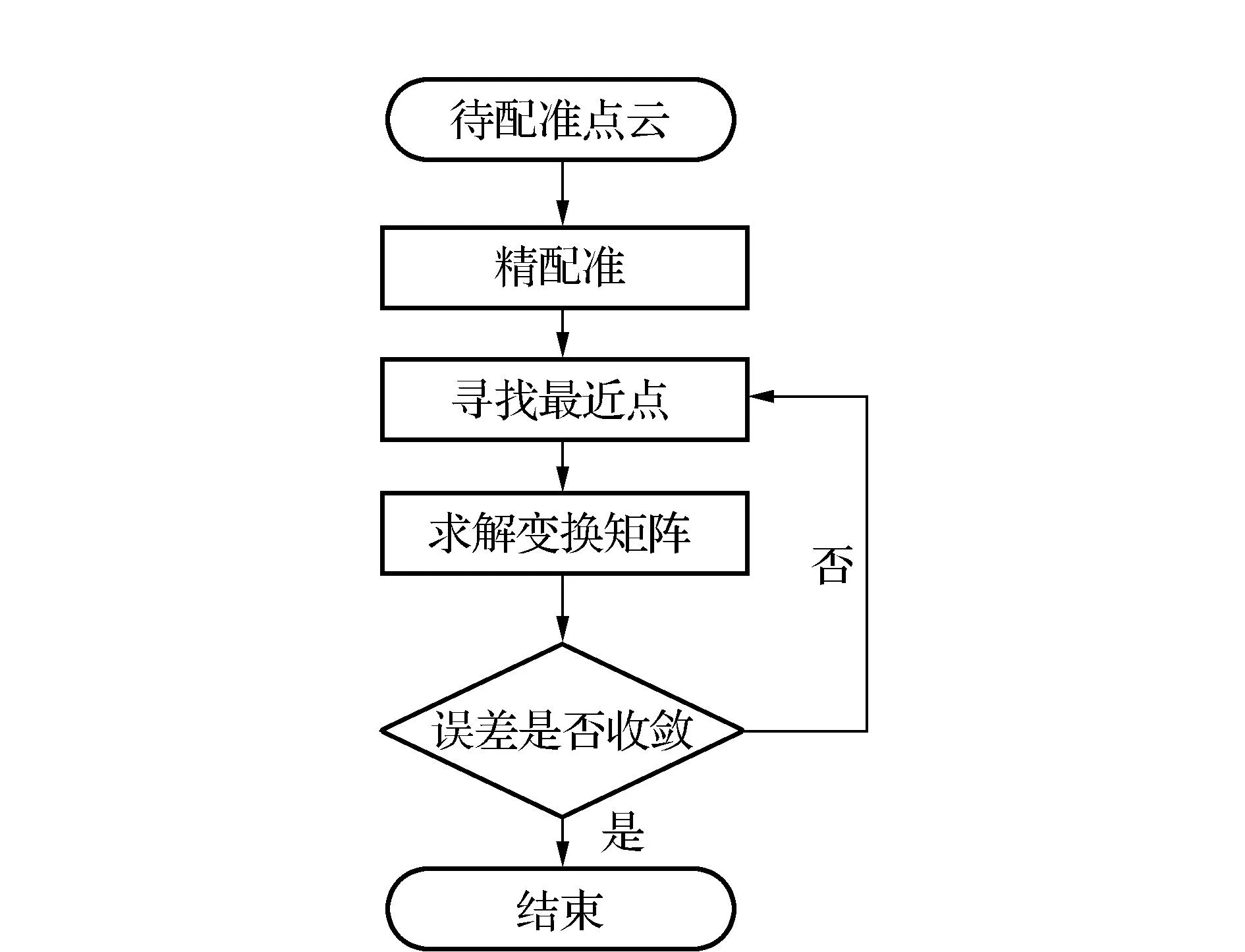
图1 ICP算法配准流程
1)将待查询的结点与所确定的分裂维的值进行比较,若小于等于分裂维的值进入左子树分子;若大于分裂维的值就进入右子树分支,这种方式循环到二叉树的叶子结点,沿着搜索路径找到处于和待查询点同一子空间的最近邻近似点;
2)对点进行“回溯”操作,若在搜索路径上结点的其它子空间结点上有更近点,则跳到子空间结点上去搜索距离最近点;
3)反复进行步骤①和②到搜素路径为空结束搜索。
2实验验证与分析
本文采用的是斯坦福Bunny点云数据,其中稀疏点云分辨率低,点云数目为112 782;密集点云分辨率高,点云数目为330 406。两组点云数据都是在不同视点下且存在着一定平移旋转平移。其中图2为2组点云数据的示意图。

图2 原始点云数据
对图2中的稀疏以及密集点云按照本文方法分别粗配准,得图3所示的点云数据粗配准结果图。

图3 点云数据粗配准结果
在图3粗配准的基础上,采用ICP对其精确配准。得图4所示的点云数据精配准结果图。

图4 点云数据ICP精配准结果
在图3粗配准基础上,采用改进ICP算法对其精配准,得图5所示点云数据精配准结果图。
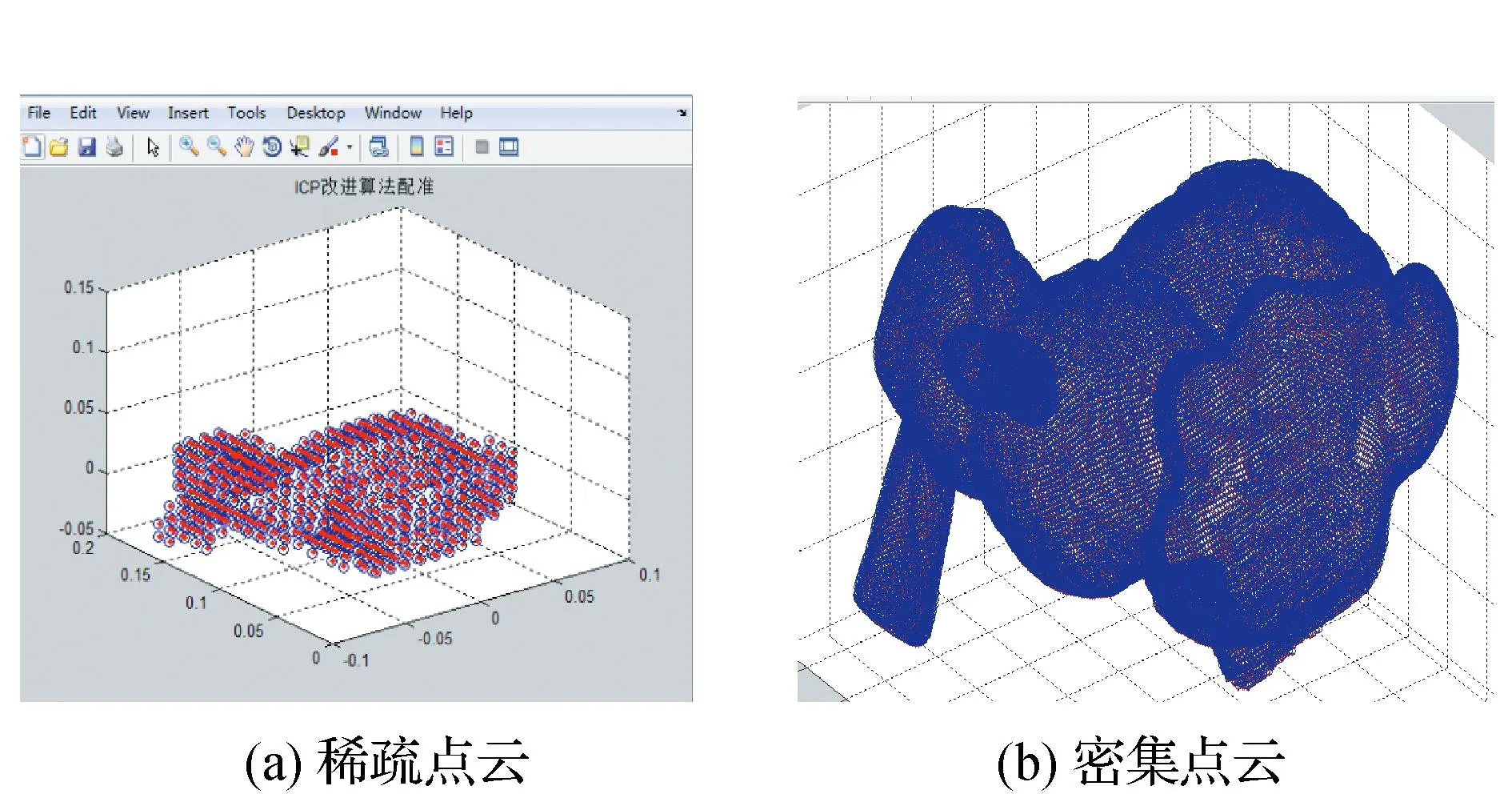
图5 改进的ICP配准结果
对实验结果分析得到传统ICP算法迭代次数与配准误差关系图,见图6;K-D树优化ICP算法迭代次数与配准误差关系图,见图7。

图6 迭代次数,误差关系
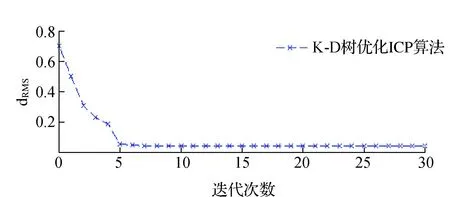
图7 改进后迭代次数,误差关系
从实验结果图6和图7上可以发现:
1)在配准误差上:前5次的迭代中误差虽然随着迭代次数的增加而逐渐减少,而在图7中前5次的迭代中误差减小的幅度大而快。传统的ICP算法误差减小的幅度要比改进的ICP算法小的多,即在误差上改进的ICP算法要优于传统的ICP;
2)在迭代次数上:在相同的15次迭代中传统的ICP算法要得到与改进后ICP算法相同的配准效果,要进行更多的迭代次数。即在迭代次数上改进的ICP算法要优于传统的ICP算法;
3)对相同两组点云数据进行配准,在配准的时间上,传统的ICP算法迭代的次数要多,误差减小的幅度要慢,改进的ICP在配准的过程中耗费的时间比传统算法小的多。传统ICP算法对点云数据进行配准耗费时间为36s,而改进后算法对点云数据进行配准耗费的时间仅为1.3s,花费的时间要比传统的ICP算法低的多。
表1说明对不同数目点云利用k-dtree改进的ICP算法进行配准比用传统的ICP算法配准耗费的时间少的多,并在点云数量较多时表现更为明显,则可得在点云配准中利用k-dtree改进的ICP算法能提高配准效率。

表1 点云实验配准时间统计
3结束语
本文采用中心重合法实现点云数据的粗配准,然后利用k-d tree快速搜索最近点对改进传统ICP方法,完成三维点云数据精配准。该方法提高三维点云数据配准的精度和速度,特别在海量点云数据和不同密度三维点云数据应用中更为明显,而且具有较好的稳定性。但是对于大型点云数据,该方法效率还是不能完全满足应用需求,在搜索策略需进一步的改善。
参考文献:
[1]张蕾,冀治航,普杰信.约束改进的ICP点云配准方法[J].计算机工程与应用,2012(18):197-200.
[2]马婷.点云数据的显示及配准[D].长春:吉林大学,2007.
[3]王蕊,李俊山,刘玲霞.基于几何特征的点云配准算法[J].华东理工大学学报(自然科学版),2009,(05):768-773.
[4]朱宁宁.基于共面条件的点云配准旋转角参数求解方法[J].测绘与空间地理信息,2015,38(5):202-205.
[5]吴禄慎,孔维敬.基于特征点的改进ICP三维点云配准技术[J].南昌大学学报(工科版),2008(3):294-297.
[6]郑德华.ICP算法及其在建筑物扫描点云数据配准中的应用[J].测绘科学,2007,32(2):31-32.
[7]吴静,靳奉祥,王健.基于三维激光扫描数据的建筑物三维建模[J].测绘工程,2007,16(5):57-60.
[8]贺磊,余春平,李广云.激光扫描数据的多站配准方法[J].测绘科学技术学报,2008,(06):410-413.
[责任编辑:李铭娜]
ICP three-dimensional point cloud registration based on K-D tree optimizationLIU Jiang1,ZHANG Xu2,ZHU Jiwen1
(1.School of Surveying and Mapping Engineering,Heilongjiang Institute of Technology,Harbin 150050,China;2.School of Mapping and City Space Information,Beijing University of Civil Engineering and Architecture,Beijing 100044,China)
Abstract:In order to improve the precision and speed of the three-dimensional point cloud registration,it presents a three dimensional point cloud registration based on ICP K-D tree optimization in this paper.First of all,the centre superposition method is adopted to realize the point cloud coarse registration,and then improve the traditional ICP where the K-D tree is used to quickly search the closest pair of points to enhance the speed of the point cloud registration.Finally the three dimensional point cloud coarse registration is completed precisely.The method overcomes the defects of the traditional ICP algorithm using Euclidean distance to determine the closest pair of points which is time-consuming and plains lots of work.On the basis of this method,the experiment can be verified through different density Bunny Stanford point cloud data.The result shows that using K-d tree optimization of ICP algorithm,the precision,speed and stability of the point cloud registration are improved when the centre superposition method is adopted to realize the three dimensional point cloud coarse registration.
Key words:point cloud registration;K-D tree;centre superposition;precision;stability
中图分类号:P208
文献标识码:A
文章编号:1006-7949(2016)06-0015-04
作者简介:刘江(1980-),男,讲师,硕士.
基金项目:黑龙江省自然科学基金资助项目(D201413)
收稿日期:2015-06-26,修回日期:2015-07-21

