多时滞的非线性微分方程的渐近稳定性

黄明辉

(广州华夏职业学院 基础部，广东 广州 510935)



多时滞的非线性微分方程的渐近稳定性

黄明辉

(广州华夏职业学院 基础部，广东 广州 510935)

摘要:以时滞的非线性微分方程为研究对象，利用不动点定理证明了时滞的非线性微分方程的渐近稳定性，并得到了零解渐近稳定的充分条件.

关键词:时滞; 渐近稳定性; 不动点； 非线性

1问题的提出

近年来，时滞微分方程的研究得到了数学、物理以及化学等多个领域学者的关注[1-2].研究下列多时滞非线性微分方程的渐近稳定性

(1)

其中bi∈C(R+,R)和τi∈C(R+,R+)，f连续可导及满足Lipschitz条件，当t→∞时，t-τi(t)→∞，i=1,2,…,N.

关于方程(1)的研究已经取得了很多研究成果[3-8].例如，Jin C H、Luo J W[3]利用Banach不动点定理证明了以下时滞微分方程的渐近稳定性

(2)

上述方程(2)是方程(1)中f(x)=x的特殊情况.当N=1和N=2，τ1=0时，方程(1)相应地改变为

x′(t)=-b(t)x(t-τ(t))

(3)

和

x′(t)=-b1(t)x(t)-b2(t)x(t-τ(t)).

(4)

Yorke J A[4]对方程(3)证明了：如果存在正数β和q，使得

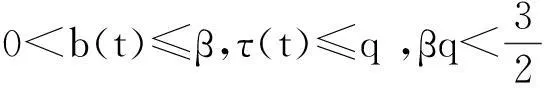
(5)

20世纪以来，Lyapunov直接法是研究微分方程零解稳定性的主要方法[10-15]. 但是，仍然存在很多问题并没有得到解决.本文仿用Jin C H和Luo J W[15]的方法，利用Banach不动点建立了新的渐近稳定性条件，并且不要求τi(t)有界，也不要求bi(t)恒正或者恒负.

2主要结论

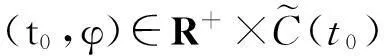
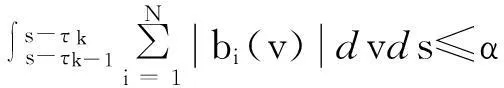
其中bi(t)在区间[m(0),∞)连续，i=1,2,…,N.

方程(1)的解渐近稳定当且仅当

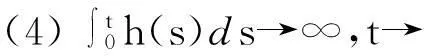
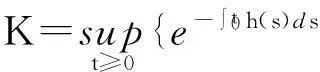
将方程(1)转换为以下形式：

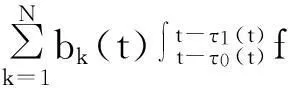
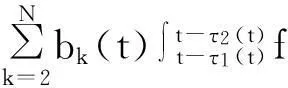
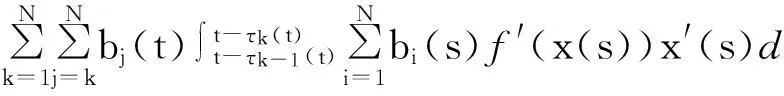
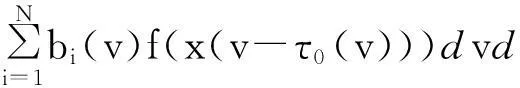
定义算子P:S→S，当t∈[m(t0),t0]时，(Px)(t)=φ(t)和t≥t0时，

(6)

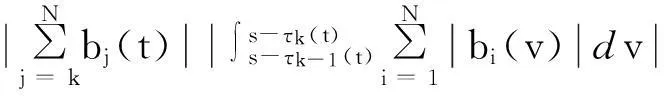
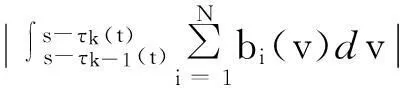
由(4) 可知，存在T3>T1，当t≥T3时

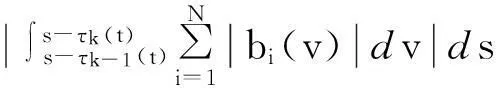
接下来，证明P是压缩映射.对任意x,y∈S，

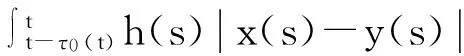
根据压缩映射原理，P在S中存在唯一的不动点x，x是方程(1)的解，即在[m(t0),t0]上且初始函数为φ(s)的解x(t)=x(t,t0,φ)→0，当t→∞时.

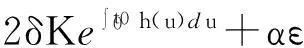
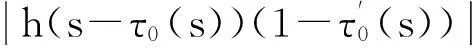
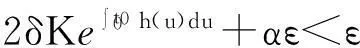
(7)

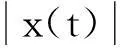
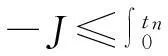
设

s≥0.

由3)可知，

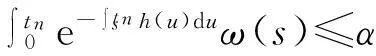
从而，有

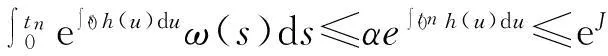
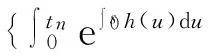
其中δ0>0，满足2δ0KeJ+α<1.

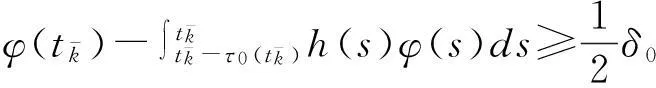
(8)

这与式(8)相矛盾，所以(4)是方程(1)的零解渐近稳定的必要条件.证明完毕.

3算例

考察以下标量方程

x′(t)=-b1(t)f(x(t-τ1(t)))-b2(t)f(x(t-τ2(t)))，

(9)

γ为充分小的正数.

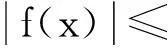
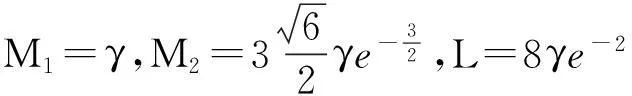
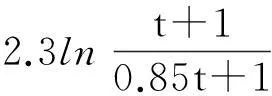
以及

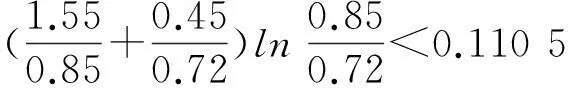
令α=0.373 8 + 0.373 8 + 0.207 2 +

因为γ是足够小的正数，可以选取充分小的γ，使得α<1，由定理1可知，方程(9)的零解渐近稳定.

参考文献：

[1] 彭世国. 中立型泛函微分方程的周期解[J]. 广东工业大学学报，1997，14(1):8-13.

PENG S G. Periodic solutions of nonlinear neutral functional differential equations[J]. Journal of Guangdong University of Technology, 1997, 14(1):8-13.

[2] 彭世国.n维无究延滞的 Liénard 型方程的周期解[J]. 广东工业大学学报，1997，14 (2):20-26.

PENG S G. Periodic solutions ofn-dimensional liénard equations with infinite retardation [J]. Journal of Guangdong University of Technology, 1997, 14 (2):20-26.

[3] JIN C H, LUO J W. Asymptotic stability of differential equations with several delays [J]. Publ Math Debrecen, 2011, 78(1):89-102.

[4] YORKE J A. Asymptotic stability for one-dimensional functional differential-delay equations [J]. Differential Equations, 1970, 7(1):189-202.

[5] KRISZTIN T. On the stability properties for one dimensional functional equations [J]. Funkcial Ekvac, 1991, 34(2):241-256.

[6] YONEYAMA T. On the stability theorem for one-dimensional functional delay-differential equation [J]. J Math Anal, 1987, 125(4):161-173.

[7] YONEYAMA T. On the stability for the delay-differential equation [J]. J Math Anal Appl, 1986, 120(1):271-275.

[8] HARA T, YONEYAMA T, MIYAZAKI R. Some refinements of Razumikhin’s method and their applications[J]. Funkciak Ekvac，1992(2), 35: 279-305.

[9] MUROYA Y. On Yoneyama’s stability theorems for one-dimensional delay differential equations[J]. J Math Anal Appl, 2000, 247(1):314-322.

[10]GRAEF J R, QIAN C, ZHANG B. Asymptotic behavior of solutions of differential equations with variable delays[J]. Proc London Math Soc, 2000, 81(1):72-92.

[11] BURTON T A. Stability by fixed point theory or Liapunocv’s theory: a comparison[J]. Fixed Point Theory , 2003, 4(1):15-32.

[12] BURTON T A, Furumochi T. Krasnoselskii’s fixed point theorem and stability[J]. Nonlinear Anal，2002, 49(4):445-454.

[13] BURTON T A. Stability by Fixed Point Theory for Functional Differential Equations[M]. New York：Dover Pubilications , 2006.

[14] ZHANG B. Fixed points and stability in differential equations with variable delay[J]. Nonlinear Anal, 2005, 63(5-7):233-242.

[15] JIN C H, LUO J W. Fixed points and stability in neutral differential equations with variable delays[J]. Proc Amer Math Soc, 2008, 136(6):909-918.

Asymptotic Stability of Nonlinear Differential Equation with Time Delays

Huang Ming-hui

(Department of Basic Education, Guangzhou Huaxia Technical College, Guangzhou 510935, China)

Abstract:This paper takes the nonlinear delay differential equation as the research subject and uses the fixed point theorem to prove asymptotic stability of nonlinear differential equations with delays. Some sufficient conditions for asymptotic stability of the trivial solution are also established.

Key words:time delays; asymptotic stability; fixed point; nonlinear

中图分类号:O175.14

文献标志码:A

文章编号:1007-7162(2016)01- 0062- 05

doi:10.3969/j.issn.1007- 7162.2016.01.012

作者简介:黄明辉(1988-)，男，助教，硕士研究生，主要研究方向为微分动力系统.

基金项目:广东省自然科学基金资助项目(S2011010005029)

收稿日期:2014- 09- 23