一种新的三维二次自治型混沌系统的分类准则

陈保颖， 高学军

(广东工业大学 应用数学学院, 广东 广州 510520)



一种新的三维二次自治型混沌系统的分类准则

陈保颖， 高学军

(广东工业大学 应用数学学院, 广东 广州 510520)

摘要:基于调控网络的观点，提出一种新的关于三维二次自治型混沌系统的分类准则.首先，把混沌系统看成生物学上的调控网络，网络中的每个节点唯一地对应于混沌系统的一个变量，通过研究调控网络的运行机制，以理解混沌产生的机制.然后，根据调控网络与三维自治多项式型混沌系统之间的关系，讨论三维二次自治型混沌系统的分类.

关键词:混沌系统； 调控系统； 混沌分类； ilinikov定理

近几十年来，尽管混沌理论及其研究内容得到了快速发展和极大丰富[1-5],但混沌研究仍很零散，缺乏系统性，研究结果极大地依赖于特定模型.混沌的传统研究思路与研究手段的局限导致混沌理论最近几十年难有突破，基本停留在早期的水平.甚至与混沌有关的某些基本问题还没有得到解决，例如：在三维自治多项式型常微分方程系统中，具有怎样结构的系统才会产生混沌；如何找出具有产生混沌潜能的所有可能系统；基于混沌的特征如何分类其中的混沌系统等.

目前为止，许多学者试图寻找三维二次多项式自治混沌系统标准型和一般性理论.特别的，关于混沌判定的理论结果主要有：Marotto定理(离散型)与i’lnikov同(异)宿轨定理(连续型)[6-7].尽管如此，如何对自治系统中的混沌进行合理分类，仍然没有系统结果，甚至相关研究也较少.然而，研究混沌系统的分类问题无论从理论研究还是从工程应用角度，都是十分重要且有意义的.

本文主要讨论三维二次多项式自治系统混沌分类的问题.关于混沌分类，目前主要有两种不同的代数准则以及一种解析分类准则：两种不同的代数准则分别由elikovsky等[8]和Yang[9]提出，这些准则是根据系统的线性化系统的系数来给出的，因此属于局部性准则.然而，一个非线性系统的线性部分往往只影响系统的局部动力学性质，混沌行为主要取决于非线性部分的影响.因此，这两种准则虽然可以对某些混沌系统进行分类，但却不能很好地揭示出混沌吸引子的几何结构和混沌的形成机制[10].周天寿提出了一种新的解析分类准则[11]，即基于i′lnikov同(异)宿轨准则，混沌系统分为4类：i′lnikov同宿轨型；i′lnikov异宿轨型；i′lnikov同异宿轨混合型以及其他类型.这种准则对现有的自治型混沌系统能够做出较为科学的分类，然而不管是利用传统意义下还是推广的i′lnikov定理来证明混沌的存在性[12]，需要事先假定系统存在一条同(异)宿轨线.由于同(异)宿轨的敏感性，因此应用中这个条件通常很难判断，这促使我们试图寻找一种更好的混沌分类方法.本文借用生物学上的调控原理将三维二次自治型混沌系统映射为调控网络，讨论网络结构分类与混沌分类之间的关系，从调控网络结构的观点提出了一种新的关于三维二次自治型混沌系统的分类准则.

1确定性方程得到网络结构图的一般规则

为了划分和理解三维二次自治多项式型动力系统的结构，以下面的二维数学模型(把x，y看做网络节点)为例给出由确定性方程得到网络结构图的一般规则：

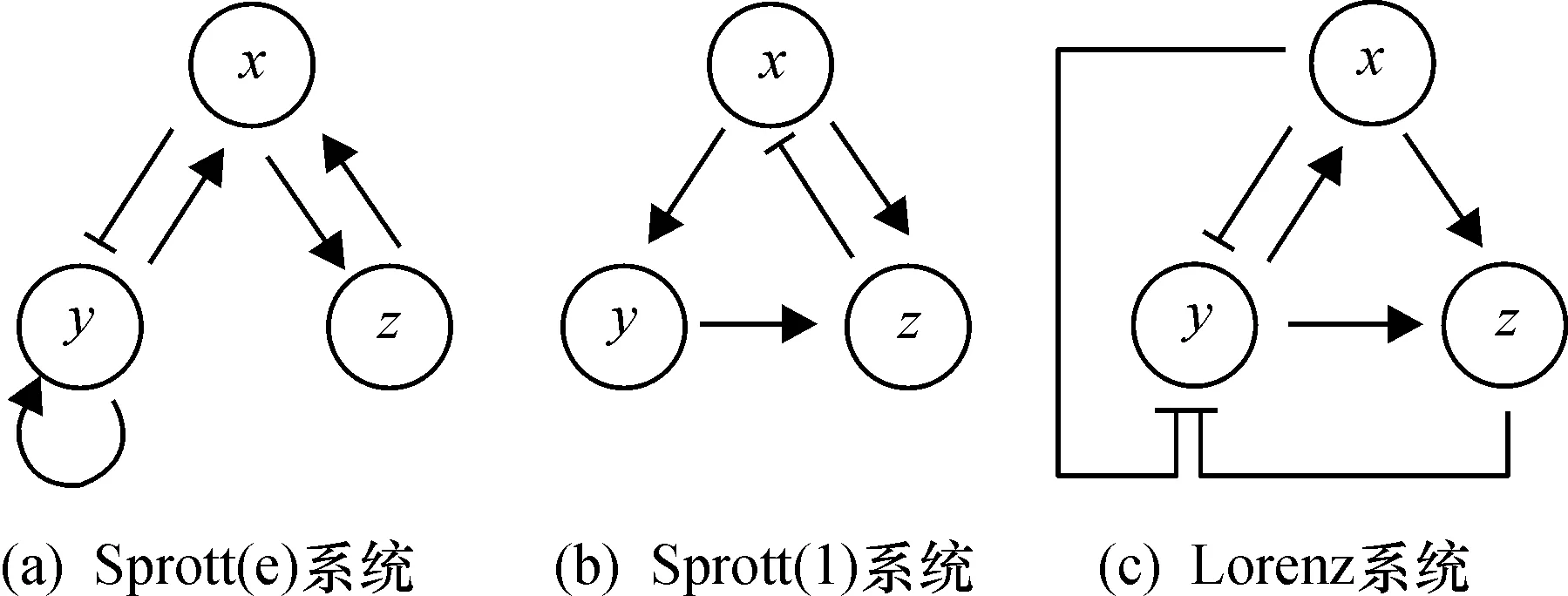
图1　混沌系统的调控网络示意图

2基于调控网络的一种新的混沌分类准则

为了从网络结构的角度对三维二次自治型混沌系统做出合理的分类,首先确定三维二次自治型混沌系统的网络结构的核心构件，如图2(b)所示.其中，数字代表各个调控网络核心构件示例，网络复杂度按照箭头方向逐渐降低.以图1(a)中Sprott(e)系统为例，其网络结构由一个正反馈和一个负反馈以及自促进耦合而成.假设删掉网络中的一条调控关系(y节点的自促进)后相应的网络仍可产生混沌性态(表明这条调控关系对混沌性态的形成仅起修饰作用)，但是继续删掉一条调控关系(x节点对z节点的促进)后，无论如何调整系统参数、变化初值条件，相应的网络都不会生成混沌，那么删掉y节点的自促进后的网络结构可看作Sprott(e)系统生成混沌的一个核心构件.然后，利用地图集策略[15]，以所有的3节点混沌调控网络作为节点构造一拓扑复杂网络，如图2(a)所示.节点的位置取决于该调控网络中调控关系的数量,如果3节点调控网络调控关系数目多，则位于网络上层，反之，位于下层；如果调控网络之间可通过添加或删除一条调控关系相互变异，则相应的节点间连通，反之，不连通.在此拓扑复杂网络中(由上至下逐层)于底层找到几种典型网络模块,它们应该是候选混沌网络的核心构件，形式相对简单并且拓扑不等价.那么由这些最简混沌网络模块的种类即可实现混沌分类的目的.

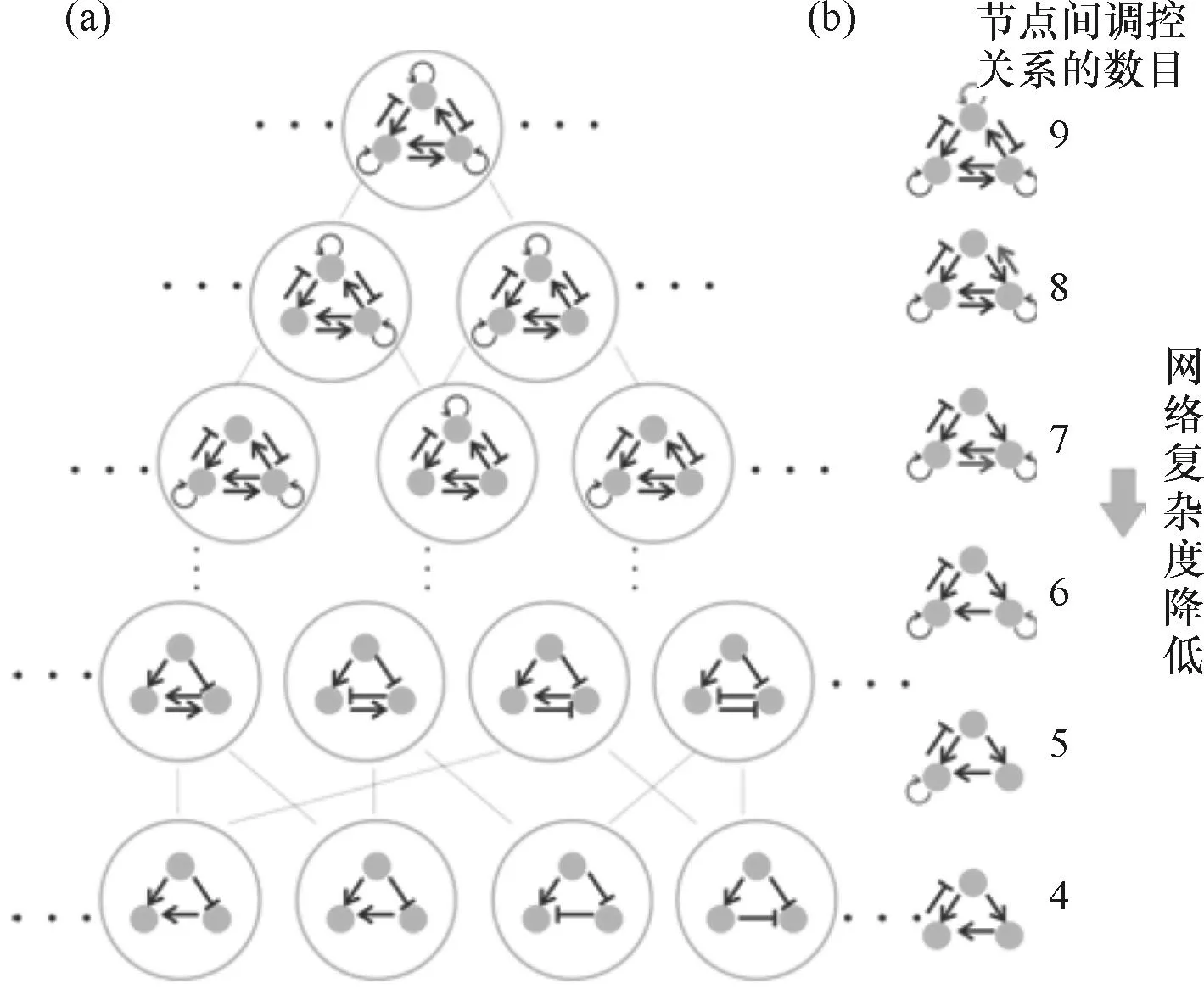
图23节点调控网络作为节点构成的拓扑复杂网络的一部分示例(a)和混沌调控网络核心构件示例(b)

Fig.2A part of the example about a 3-node network as nodes of the topologically complex network(a) and the example of how to determine the chaotic regulatory network core(b)

3结论

本文基于调控网络的观点提出了一种新的关于三维二次自治型混沌系统的分类准则.从系统结构的角度来研究混沌的产生机制，利用生物学上的调控网络理论来研究混沌产生与系统结构之间的关系，这种新的研究方法将对揭示混沌的本质机制有重要帮助.

参考文献：

[1]LEONOV G A, KUZNETSOV N V, VAGAITSEV V I. Hidden attractor in smooth Chua system[J]. Physica D, 2012, 241(18): 1482-1486.

[2] JAFARI S, SPROTT J C. Simple chaotic flows with a line equilibrium[J]. Chaos Solit Fract, 2013, 57: 79-84.

[3] JAFARI S, SPROTT J C, Golpayegani S. Elementary quadratic chaotic flows with no equilibria[J]. Phys Lett A, 2013, 377(9): 699-702.

[4]赵舒阳,刘伟,蔡耀河.一种改进的混沌局部搜索的人工蜂群算法[J]. 广东工业大学学报,2013,30(4): 55-60.

ZHAO S Y, LIU W, CAI Y H. Artificial bee colony algorithm based on improvement of chaotic local search[J]. Journal of Guangdong University of Technology, 2013,30(4): 55-60.

[5] 禹思敏.网格多翅膀超混沌系统的构造与生成[J].广东工业大学学报,2014,31(2): 1-6.

YU S M. Construction and generation of grid multi-wing hyperchaotic systems[J]. Journal of Guangdong University of Technology, 2014,31(2): 1-6.

[6] MAROTTO F R. Snap-back repellers imply chaos in Rn[J]. J Math Anal Appl, 1978, 63: 199-223.

[9] YANG Q G. A chaotic system with one saddle and two stable node-foci[J]. Int J Bifur Chaos, 2008, 18(5): 1393-1414.

[10] LÜ H, CHEN G R. Generating multiscroll chaotic attractors: theories, methods and applications[J]. Int J Bifur Chaos, 2006,16(4): 775-858.

[11] ZHOU T S, CHEN G R. Classification of chaos in 3-D autonomous quadratic systems-I. basic framework and methods[J]. Int J Bifur Chaos, 2006, 16(9): 2459-2479.

[12] ZHENG Z H, CHEN G R. Existence of heteroclinic orbits of thei′lnikov type in a 3D quadratic autonomous chaotic system[J]. J Math Anal Appl, 2006, 315(1): 106-119.

[13] SPROTT J C. Some simple chaotic flows[J]. Phys Rev E, 1994, 50(2): 647-650.

[14] LORENZ E N. Deterministic nonperiodic flow[J]. J Atmos Sci, 1963, 20: 130-141.

[15] COTTERELL J, SHARPE J. An atlas of gene regulatory networks reveals multiple three-gene mechanisms for interpreting morphogen gradients[J]. Molecular Systems Biology, 2010, 6(1): 425- 439.

New Classification Rules of 3-D Quadratic Autonomous Chaotic System

Chen Bao-ying, Gao Xue-jun

(School of Applied Mathematics, Guangdong University of Technology, Guangzhou 510520, China)

Abstract:This paper discusses the classification rules of chaos in 3-dimensional quadratic autonomous systems. The author develops a new effective classification and provides a basic classification framework. Based on regulatory network, the research first views a chaotic system as a regulatory network in which every node corresponds uniquely to a variable in the chaotic system. Then, it studies the relationship between regulatoy networks of 3 nodes and 3-dimensional autonomous chaotic system of polynomial type. Finally, the paper classifies 3-dimensional autonomous chaotic systems of polynomial type from the viewpiont of regulatory network.

Key words:chaotic system; regulatory system; chaos classification; ilinikov theorem

中图分类号:N93

文献标志码:A

文章编号:1007-7162(2016)01- 0026- 03

doi:10.3969/j.issn.1007- 7162.2016.01.005

作者简介:陈保颖(1980-)，女，讲师，主要研究方向为混沌的控制与反控制. E-mail：sunnycby@126.com.通信作者: 高学军(1962-)，女，副教授，主要研究方向为微分方程数值计算. E-mail：gaoxxj@163.com.

基金项目:国家自然科学基金资助项目(11326130，11501128);广东省对外科技合作项目(2013B051000075)

收稿日期:2015- 05- 14