基于两垂直方向虚拟平移的波达方向判定算法

肖志贤，林福民

(广东工业大学 物理与光电工程学院， 广东 广州 510006)



基于两垂直方向虚拟平移的波达方向判定算法

肖志贤，林福民

(广东工业大学 物理与光电工程学院， 广东 广州 510006)

摘要:提出了一种针对均匀圆阵接收信号波达方向(direction of arrival，DOA)判定的算法，该算法相对于其他算法，更能充分利用信号中的有用信息，达到提高算法判定精度的目的.算法将接收信号数学模型在Z轴和X轴方向分别进行虚拟平移，通过模式激励，构造出两个包含接收信号DOA信息的满秩Toeplitz矩阵，达到相干信号解相干的目的.先后根据Z轴、X轴方向旋转因子特性的不同，先得出信号俯仰角的估计值，再得出方位角的估计值，完成二维波达方向的判定.仿真结果验证了该算法对于相干信号DOA判定的正确性，而且对于强相干和低信噪比的入射信号DOA也能有效区分和判定.

关键词:均匀圆阵； 波达方向估计； Toeplitz矩阵

智能天线技术[1-4]的关键技术之一就是对各种入射信号波达方向DOA (direction of arrival)进行判定，为了更好地实现此功能，必须采用阵列天线，相比于均匀线阵，均匀圆阵具有可实现360°全方位和二维角无模糊覆盖的优点，所以近年来得到了广泛的关注[5-7]，然而，均匀圆阵接收信号的阵列流型不具备范德蒙德形式，以致传统算法如多重信号分类[8](multiple signal classification, MUSIC)算法、旋转不变信号参数估计[9](estimation of signal parameter via rotational invariance techniques，ESPRIT)算法等子空间类算法无法直接运用于均匀圆阵的DOA估计.文献[10]提出了MODE-TOEP算法，该算法采用模式激励技术，将均匀圆阵转化为虚拟的均匀线阵，构建包含DOA信息的满秩Toeplitz矩阵，达到解相干目的，通过谱峰搜索，完成DOA估计，该算法可以有效分辨相干信号的DOA，弥补了传统MUSIC算法只适用于非相干信号的缺陷，但该算法不能充分地对强相关和低信噪比信号进行有效的分辨，为此，文献[11]在均匀圆阵接收信号数学模型基础上，将阵列信号往Z轴方向虚拟平移，构建了波达方向矩阵，实现了对相干入射信号DOA二维角的判定，提高了算法的分辨率，但同时由于应用波达方向矩阵是以损失子阵列孔径为代价的，一定程度上造成了阵列资源的浪费.文献[12]提出了一种圆阵垂直平滑解相干算法，但对于阵列信号数学模型而言，由于均匀圆阵的高度对称性，X轴方向的虚拟平移与Y轴方向的虚拟平移等价，因此该算法在X轴、Y轴两方向上重复平移只是对阵列接收信号DOA信息的重复利用，并不能达到提高算法估算精度的目的，而且算法中只针对了入射信号一维角的判定，不能发挥均匀圆阵能对入射信号DOA二维角判定的优势.

本文基于均匀圆阵信号数学模型，提出了一种基于两垂直方向虚拟平移的DOA算法，该算法的独特性主要体现为利用阵列信号在Z轴、X轴方向相位旋转因子特性的不同，将阵列信号在Z轴、X轴方向进行虚拟平移，构造两个Toeplitz矩阵，利用信号子空间和噪声子空间的正交特性，先对俯仰角进行估计，然后对方位角进行估计，完成均匀圆阵相干信号的DOA估计.该算法与其他虚拟平移算法相比而言，不是对DOA信息进行简单的重复利用后取均值，而是根据两垂直方向旋转因子不同，从不同层面对DOA信息进行进一步虚拟扩展处理，充分利用了阵列接收信号中的DOA信息，提高了算法的分辨率，与此同时，由于是虚拟平移后的阵列信号处理，避免了阵列资源的浪费.仿真对比结果表明，对于低信噪比情况下的相干信号，该算法能有效减小其DOA估算误差、提高DOA估算精度.

1数学模型

假设在系统中有K个窄带远场信号入射到如图1所示的均匀圆阵中，该圆阵以圆心为参考点，由M个同性阵元组成，模型中采用前L个信号为相干信号，其余(K-L)个信号为非相干信号，不考虑阵元与阵元之间的互耦效应，则第k个阵元的接收信号可以表示为

(1)

其中，si(t)为第i个信号信号幅度，r为均匀圆阵半径，λ为入射波波长，nk(t)为功率σ2空域白噪声且与各信号互不相干，βi=ρiejΔφi，i= 1,2,…,L为信号的衰减系数假设(β1= 1, Δφ1= 0)[13].

图1　均匀圆阵

阵列接收信号矢量可以表示为

X(t)=[x1(t),x2(t),…,xM(t)]T=AS(t)+N(t)，

(2)

式中S(t)=[s0(t),s1(t),…,sK-1(t)]T为阵列入射信号矢量，N(t)=[n0(t),n1(t),…,nK-1(t)]T为噪声矢量，A=[a(θ0,φ0),a(θ1,φ1),…,a(θK-1,φK-1)]为阵列流型矢量.另外，

(3)

为均匀圆阵的方向矢量，其中，rk= 2πk/M，k= 0,1,…,M-1，可以看出，均匀圆阵的方向矢量不具备有范德蒙德形式，为了使均匀线阵的解相干算法可以直接应用到均匀圆阵，需采用模式激励将均匀圆阵转化为虚拟均匀线阵[14]

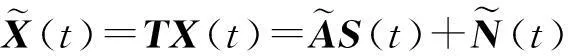
(4)

转化矩阵T为T = J-1F/M，式中

F=[w-k,w-k+1,…,wk]H，

(5)

wk=[1,ej2πk/M,…,ej2πk(M-1)/M]H，

(6)

J=diag{1/jkJk(β)}.

(7)

令h≈2πR/λ为模式激励的最大模式数，则k=-h,…,0,…,h，Jk(β)为k阶第一类贝塞尔函数.假如满足M>2h+1，虚拟线阵的阵列流型为

(8)

可以看出，转化后的虚拟线阵阵列流型具有范德蒙德形式，可将均匀线阵的解相干算法用于均匀圆阵DOA估计.

2垂直方向虚拟平移DOA判定算法

均匀圆阵阵列接收信号矢量为

X(t)=[x1(t),x2(t),…,xM(t)]T=AS(t)+N(t)，

(9)

将其往X轴方向平移n次，第m次平移的相位旋转因子为

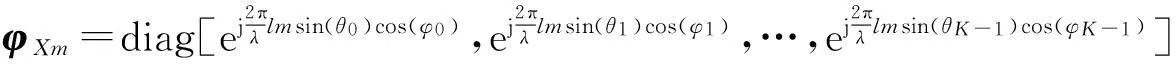
(10)

m= 1,2,3,…,n，其中l为阵列信号每次平移的距离，平移后的第m个阵列接收信号矢量为

Xxm(t)=[x1(t),x2(t),…,xM(t)]T=

AφXmS(t)+N(t).

(11)

阵列接收信号矢量往Z轴方向平移p次，第q次平移的相位旋转因子为

(12)

q= 1,2,3,…,p，其中，l为阵列信号每次平移的距离，平移后的第q个阵列接收信号矢量为

Xzq(t)=[x1(t),x2(t),…,xM(t)]T=

AφZqS(t)+N(t).

(13)

用模式激励方法，将平移后X轴、Z轴方向上信号矢量分别转化为具有K= 2h+1个模式元素的对称虚拟均匀线阵，如图2所示.

图2　虚拟均匀线阵

接收信号矢量可表示为

(14)

Z轴上有p个均匀线阵，第q个阵列接收信号协方差矩阵可表示为

(15)

Rss=E[s(t)s(t)H]为有用信号的协方差矩阵；I2h+1为(2h+1)×(2h+1)单位矩阵.式(15)协方差矩阵的第m行、第n列的元素可表示为[13]

(16)

m,n=-h,…,0,…,h.

(17)

(18)

(19)

RZToep=

(20)

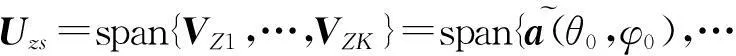
(21)

(22)

同样，X轴上有n个均匀线阵，第m个阵列接收信号协方差矩阵可表示为

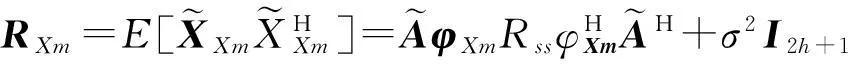
(23)

Rss=E[s(t)s(t)H]为有用信号的协方差矩阵；I2h+1为(2h+1)×(2h+1)单位矩阵.式(23)协方差矩阵的第m行、第n列的元素可表示为

(24)

其中dm,n、σ2、δm,n定义与之前所述一样，以矩阵RXm第m行元素构成包含DOA估计信息的Toeplitz矩阵：

RXToep=

(25)

同理分析，矩阵为满秩，照样可以达到解相干的目的,对RXToep进行特征值分解，同样可得到K个大特征值和M-K+1个小特征值，相应特征向量空间为

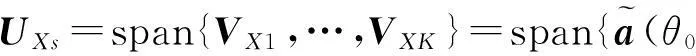
J(φXm(k,:))=

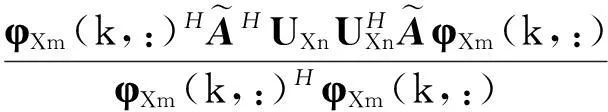
(26)

(27).

完成信号二维角的波达方向估计.

3算法步骤

(1) 利用模式激励将均匀圆阵转换为均匀线阵；

(2) 利用相位旋转因子式(10)和式(12)将均匀线阵分别在X轴、Z轴方向进行虚拟平移；

(3) 分别得出虚拟平移后的信号协方差矩阵，利用式(20)和式(25)构造相应的Toeplitz矩阵；

(4) 首先对Z轴方向上构造的Toeplitz矩阵特征分解，利用式(21)最小值，求出俯仰角的估计值；

(5) 对X轴方向上构造的Toeplitz矩阵特征分解，利用式(26)最小值，求出来波方位角的估计值，完成信号二维角的波达方向估计.

4仿真结果分析

为验证算法的可行性和有效性，本文进行了Matlab仿真实验.仿真DOA算法估计性能、均方根误差实验中采用(仿真图中二维空间谱估计及DOA估计角度单位均为度)：

(1) 8阵元均匀圆阵，阵间间距为d=λ/2；

(2) 激励模式的最大模式数h=3，可激发2h+1个相位模式，形成阵元数为7的虚拟均匀线阵；

(3) 在X轴、Z轴方向上，每次平移的距离为0.1r(r为均匀圆阵半径)；

(4) 3个入射角信息，其中信号1为独立信号，信号2、信号3为强相干信号，入射角度分别为：(θ1,φ1) =(80°,70°)、(θ2,φ2) =(90°,75°)、(θ3,φ3) =(150°,50°).

图3、图4中所示为信噪比SNR=20 dB、快拍数为1 024、基于两垂直方向虚拟平移的波达方向判定算法的空间谱估计以及入射信号俯仰角、方位角的来波方向估计，从两图中可以看出，当入射信号为强相干信号，入射角度比较邻近时，该算法能够很好地抑制相干信号之间的干扰，也能够精确地估算出入射信号的来波方向，精确度较高.

图5所示为本文算法与文献[8]MODE-TOEP算法与文献[10]垂直平滑算法在不同信噪比条件下DOA估计的均方根误差关系曲线图.由图5可见，在信噪比SNR<15 dB情况下，本文算法相对于MODE-TOEP算法和垂直平滑算法而言，DOA估计的误差及波动更小，估计精度更高.当SNR>15 dB，3种算法性能均趋于稳定.仿真实验表明，基于两垂直方向虚拟平移的波达方向估算算法在低信噪比环境中，比MODE-TOEP算法[8]和垂直平滑算法[10]DOA估计误差更小，估计精度更高.

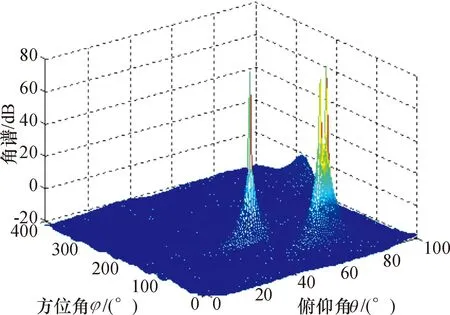
图3　二维空间谱估计

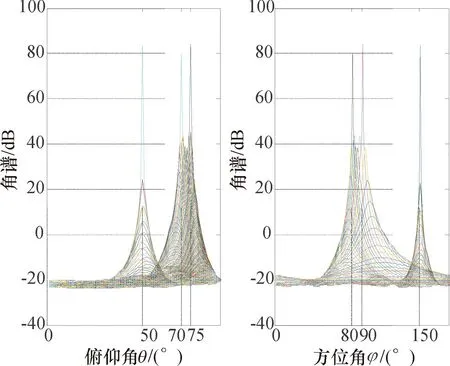
图4　DOA估计

图5　均方根误差与信噪比关系曲线图

Fig.5Graph of root mean square error and signal-to-noise ratio

图6所示为本文算法在不同信噪比下均匀圆阵阵元数M分别为6、8、10的均方根误差曲线图，由图6可见，随着阵元数的增加，二维估计角度均方根误差不断减小，估计精度相应提高.这是由于均匀圆阵阵元数增加，转化为虚拟均匀线阵的相位模式相应增加，使得接收数据中含DOA估计信息更加丰富具体.但与此同时，阵元数增加会导致硬件成本的增加，所以，在实际应用中，估算精度和阵元数目还应折衷处理.

图6　不同阵元数下均方根误差曲线图

5结论

本文提出了一种基于两垂直方向虚拟平移的Toeplitz矩阵算法.该算法利用阵列信号在Z轴、X轴方向上旋转因子的不同，将信号在Z轴、X轴两垂直方向上进行虚拟平移，经过模式激励，将均匀圆阵转化为阵列流型具有范德蒙德形式的虚拟均匀线阵，构造两个包含DOA估计信息的Toeplitz矩阵，利用信号子空间和噪声子空间的正交特性，完成均匀圆阵相干信号的DOA估计.仿真对比实验验证了算法对于提高均匀圆阵相干信号尤其是在低信噪比情况下DOA估算精度的可行性和有效性.同时，在实际应用中，针对算法在Z轴、X轴方向上每次平移的距离对算法性能的约束问题，还有待进一步研究讨论.

参考文献：

[1]LIBERTI J C, RAPPAPORT T S. Smart antennas for wireless communications: IS-95 and third generation CDMA applications [M]. New York: Prentice Hall PTR, 1999.

[2] ALEXIOU A, HAARDT M. Smart antenna technologies for future wireless systems: trends and challenges[J]. IEEE Communications Magazine, 2004, 42(9): 90-97.

[3] 李庚禄， 林福民， 张华福. 表面开十字形辐射槽的新型GNSS贴片天线的研究和应用[J]. 广东工业大学学报，2014，31(2): 90-94.

LI G L, LIN F M, ZHANG H F. Research and application of a novel GNSS microstrip patch antenna with a cross slot cut in the patch[J]. Journal of Guangdong University of Technology, 2014, 31(2): 90-94.

[4] 汪雪刚， 李瑞， 吴多龙, 等. GPS 双频圆极化微带天线的设计[J]. 广东工业大学学报， 2011， 28(2): 43-46.

WANG X G, LI R, WU D L, et al. The design of dual-band circularly polarized patch antenna for GPS[J]. Journal of Guangdong University of Technology, 2011, 28(2): 43-46.

[5] IOANNIDES P, BALANIS C A. Uniform circular arrays for smart antennas[J]. IEEE Antennas and Propagation Magazine, 2005, 47(4): 192-206.

[6] WEBER R J, HUANG Y. Performance analysis of direction of arrival estimation with a uniform circular array[C]// Aerospace Conference, 2012. [S.l.]: IEEE, 2012:1-7.

[7] ASKARI M, KARIMI M. Sector beamforming with uniform circular array antennas using phase mode transformation[C]// Iranian Electrical Engineering Conference, 2013. [S.1.]: IEEE, 2013:1-6.

[8] SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]. Antennas and Propagation, IEEE Transactions on, 1986, 34(3): 276-280.

[9] ROY R, PAULRAJ A, KAIATHh T. ESPRIT——A subspace rotation approach to estimation of parameters of cisoids in noise[J]. Acoustics, Speech and Signal Processing, IEEE Transactions on, 1986, 34(5): 1340-1342.

[10]SHUYAN G, HUI C, YONGLIANG W, et al. A novel algorithm for estimating DOA of coherent signals on uniform circular array[C]// Radar Conference, 2006. [S.l.]：IEEE, 2006: 1-4.

[11] 毛维平, 李国林, 谢鑫. 均匀圆阵相干信源二维波达方向估计[J]. 系统工程与电子技术, 2013, 35(8): 1596-1601.

MAO W P, LI G L, XIE X. 2D-DOA estimation of coherent signals based on uniform circular array[J]. System Engineering and Electronic, 2013, 35(8): 1596-1601.

[12] 杨逸, 曹祥玉, 杨群. 一种圆阵垂直平滑解相干算法[J]. 火力与指挥控制, 2012, 37(9): 141-142.

YANG Y, CAO X Y, YANG Q. The coherent DOA estimation of uniform circular array based on SVD algorithm[J]. Fire Control & Command Control, 2012, 37(9): 141-142.

[13] HAN F M, ZHANG X D. An ESPRIT-like algorithm for coherent DOA estimation[J]. Antennas and Wireless Propagation Letters, IEEE, 2005, 4(1): 443-446.

[14] 杨益新, 孙超. 圆阵相位模式空间波束输出的高分辨目标方位估计算法研究[J]. 信号处理, 2000, 16(2): 121-125.

YANG Y X, SUN C. Studies on high resolution bearing estimation algorithms to beam outputs in phase mode space of circular arrays[J]. Signal processing, 2000, 16(2): 121-124.

[15] YAN H, FAN H H. On source association of DOA estimation under multipath propagation[J]. Signal Processing Letters, IEEE, 2005, 12(10): 717-720.

Algorithm of Direction of Arrival Estimation Based on Virtual Translation in Two Vertical Directions

Xiao Zhi-xian, Lin Fu-min

(School of Physics and Optoelectronic Engineering, Guangdong University of Technology, Guangzhou 510006, China)

Abstract:A new algorithm aiming at improving the estimation accuracy of direction of arrival (DOA) based on uniform circular array (UCA) has been proposed in this paper. Compared with other algorithms, the new proposed one can make the most of the useful information hiding in the received signal by shifting virtually in two vertical direction. Firstly, it shifts the mathematical mode of array received signals at the z axis and x axis respectively with the method of mode excitation. And then, two new full rank Toeplitz matrices relating to the information of DOA estimation have been reconstructed so the purpose of decorrelation has been achieved. Through the different properties of rotation factor at z axis and x axis successively, the researchers obtain the estimation of pitch angle and then the estimation of azimuth angle. Result analysis of simulation shows the validity of the DOA estimation of coherent signal as well as the strong coherence and low SNR incoming signals.

Key words:uniform circular array (UCA); direction of arrival (DOA) estimation; Toeplitz matrix

中图分类号:TN 911.7

文献标志码:A

文章编号:1007-7162(2016)01- 0045- 06

doi:10.3969/j.issn.1007- 7162.2016.01.009

作者简介:肖志贤(1990-)，男，硕士研究生，主要研究方向为智能天线阵列信号处理.

基金项目:广州市科技计划项目(201510010093)

收稿日期:2014- 11- 19