浅谈面积法在几何证明中的应用

杨敏欣

（福建省惠安第五中学）

浅谈面积法在几何证明中的应用

杨敏欣

（福建省惠安第五中学）

在初中几何题中，经常会碰到一些和垂线段有关的问题，这就要求学生要懂得利用特殊位置法猜测垂线段之间的数量关系，善于构造三角形并利用三角形面积之间的数量关系证明结论。

面积法；垂线段；等边三角形；几何证明

探究内容：

①探究直角三角形三边与斜边上的高的数量关系。

②如图2，等腰△ABC中，AB=AC，P是底边BC上一动点P到两腰的距离分别为PE、PF，PE+PF是一个定值吗？该定值会等于谁？证明你的猜想。

如果P点在BC或CB的延长线上，你又能得到什么结论?

把等腰三角形改成等腰梯形，还有同样的结论吗？

③如图3，在矩形ABCD中，P是AB上一动点，PE⊥AC于E，PF⊥BD于F，PE+PF是一个定值吗？本探究题和探究②有联系吗？

④如图4，等边△ABC中，P是三角形内任意一点P到三边的距离分别为PD、PE、PF，PD+PE+PF是定值吗？该定值会等于谁？证明你的猜想。当P点在等边三角形ABC外部时,上述的和还会是定值吗？

图1

图2

图3

图4

如果P点在△ABC外，你又能得到什么结论？

探究①：如图1，设AB=c，BC=a，AC=b，AD=h，由三角形面积可得S△ABC=bc=ah，∴h=。

探究②：（1）如图2，当P点在线段BC上，设h为△ABC中BC边上的高。

图2 -1

因而可得PE+PF的和是一个定值。

（2）如图2-2，当P点在线段CB的延长线上，设h为△ABC中BC边上的高，连接AP

因而PF-PE的差是一个定值。

同理可证，当P点在BC的延长线上，PE-PF的差也是一个定值，为

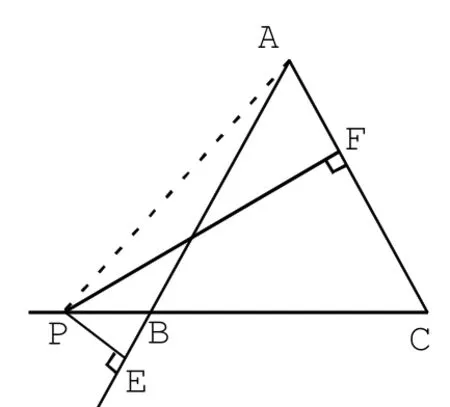
图2 -2

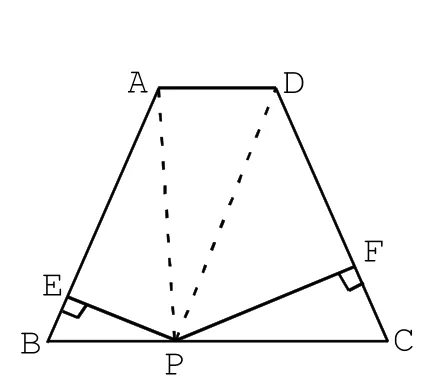
图2 -3

当把等腰三角形改为等腰梯形时，

（1）如图2-3，当动点P在BC线段上运动，连接AP和DP，设h为等腰梯形ABCD的高，

（2）如图2-4所示，当动点P在BC线段的延长线上运动时，连接AP和DP

图2 -4

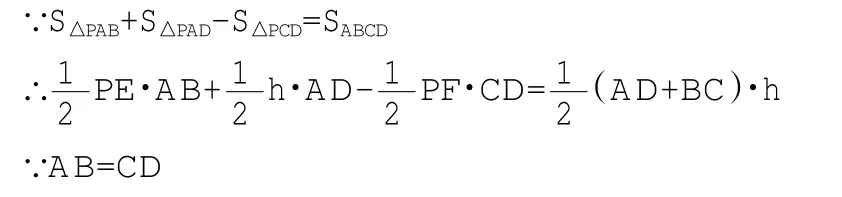
同理可证，P点在CB的延长线上，PF-PE的差也是一个定值，PE-PF=

结论：当把等腰三角形改为等腰梯形时，动点P在线段BC上运动时，PE+PF的和是一个定值，为；当动点P在BC或 CB的延长线上为定值。

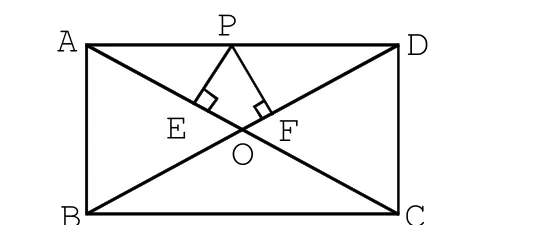
图3

探究④：（1）如图4-1，当P点在三角形ABC内部时，连接AP和BP，CP

故PE+PF+PD的和为定值。

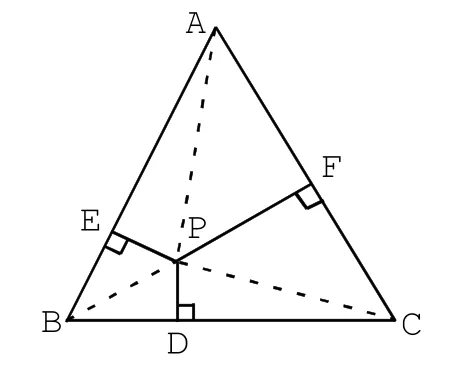
图4 -1

图4 -2

（2）如图4-2，当P点在三角形ABC外部时，连接AP和BP，CP

故PE+PF-PD的值为定值。

［1］朱德祥，朱维宗.初等几何研究［M］.高等教育出版社，2003.

［2］余昌红.浅谈等面积法在几何题中的应用［J］.新课程导学，2011（13）.

·编辑 谢尾合