在学习相似三角形时要重视对应关系

金银千

（江苏省盐城市尚庄初级中学）

在学习相似三角形时要重视对应关系

金银千

（江苏省盐城市尚庄初级中学）

在学习相似三角形时，课本特别强调：“表示两个三角形相似时要把对应顶点写在的对应位置上.”也就是说，教师要重视相似三角形中的对应关系.但是，在解决三角形相似的一些实际问题时，有不少同学往往会忽略这一点.

相信；重视；对应关系

例1.S老师提出这样一道思考题：如图1，梯形ABCD中，AD∥BC，对角线AC、BD相交于点O，试问△AOB与△DOC是否相似？

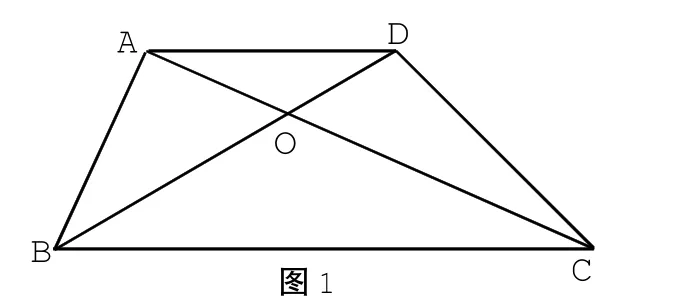
Z同学对此作了如下解答：

答：△AOB∽△DOC理由：因为AD∥BC，所以△AOD∽△BOC，所以，所以，又因为∠AOB=∠DOC，所以△AOB∽△DOC.

你认为该同学的解答是否正确？并说明理由.

分析：表面看来，这个同学的解答好像是没有问题的，但事实上△AOB与△DOC不一定相似，问题出在哪里呢？仔细推敲他的解答过程，由AD∥BC，可知∠DAO=∠BCO，∠ADO=∠CBO，那么这两个相似三角形的三组对应顶点分别为A与C，D与B，O与O，则Z同学的解答中“△AOD∽△BOC”的正确写法为：△AOD∽△COB.从而此相似三角形的对应边成比例的比例式应为，观察此比例式可知，成比例的四条线段不能构成△AOB与△DOC的对应边，因此，不能判定△AOB与△DOC相似.由此可知，该同学的解答不正确.

例2.一个钢筋三脚架三边长分别是20cm、50cm、60cm，现要再做一个与其相似的钢筋三脚架，而只有长30cm和50cm的两根钢筋，要求以其中的一根为一边，从另一根上截下两段（允许有余料）作为另两边，则此钢筋三脚架三边所有可能的长度为____.

错解：将50cm的钢筋截成两段，并设截成的两段的长分别为xcm和ycm.

因为要做的一个钢筋三脚架与原钢筋三脚架相似，则根据相似三角形的对应边成比例，可得，解之得x=10，y= 25.所以此钢筋三脚架的三边长分别为10cm、25cm、30cm.

分析：解决此题的关键是运用相似三角形的对应边成比例，求截得两边的长.而此题中的边的对应关系显然具有不确定性，因此，确定边的对应关系又是解决这个问题的前提条件和关键，错解就是忽略了这一点.

正解：以30cm的钢筋为一边时，设另两边的长分别为xcm和ycm.因要做的一个钢筋三脚架和原钢筋三脚架相似，则根据边的对应关系，可得比例式或或，解之得x=75，y=90（不满足x+y≤50，舍去）或x=12，y= 36或x=10，y=25.

以50cm的钢筋为一边时，设另两边的长分别为xcm、ycm则x+y≤30＜50，两边之和小于第三边，不能构成三角形.

因此，此钢筋三脚架三边的长分别为12cm、30cm、36cm或10cm、25cm、30cm.

例3.如图2所示，在矩形ABCD中，AB=12cm，BC=6cm，点P沿AB边从点A开始向点B以2cm/s的速度移动，点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发，用t（秒）表示移动的时间（0≤t≤6），试问：t为何值时，以点Q、A、P为顶点的三角形与△ABC相似？错解：当△QAP与△ABC相似时，有，即，解之，得t=1.2

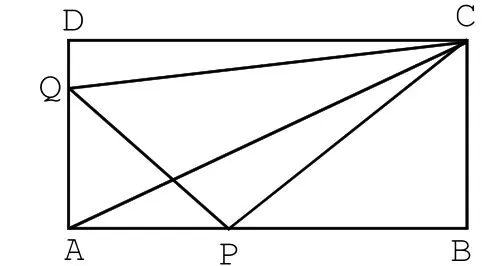
图2

答：t为1.2秒时，以点Q、A、P为顶点的三角形与△ABC相似.

分析：由题意，知∠QAP=∠B=90°，要求以QAP为顶点的三角形与△ABC相似，另一组对应角尚不明确，故需要分类讨论.

因为∠QAP=∠B=90°，故

（1）当∠AQP=∠BAC时，有Rt△AQP∽Rt△BAC，得即，解之得t=1.2（2）当∠AQP=∠BCA时，有Rt△AQP∽Rt△BCA，可得，即，解之得t=3

答：t为1.2秒或3秒时，以点Q、A、P为顶点的三角形与△ABC相似.

重视相似三角形中的对应关系，注意对“对应”的理解，一方面能使我们易于分清相似三角形中对应的边和角，另一方面还能使我们进一步理清实际问题中的各种可能。

［1］刘学俊.“用相似三角形解决问题2”教学设计［J］.数学学习与研究，2016（15）.

［2］张翔.例说相似三角形的综合运用［J］.中学生数学，2016（18）.

·编辑 谢尾合