基于最小平方距离的区间值合作对策求解模型与方法

李登峰，刘家财,2

(1.福州大学经济与管理学院，福建 福州 350108；2.福建农林大学交通与土木工程学院，福建 福州 350002)

基于最小平方距离的区间值合作对策求解模型与方法

李登峰1，刘家财1,2

(1.福州大学经济与管理学院，福建 福州 350108；2.福建农林大学交通与土木工程学院，福建 福州 350002)

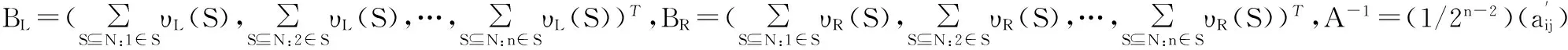
区间值合作对策；最小平方法；损失函数；配送联盟；数学规划

1 引言

由于管理决策环境与条件的不确定性、信息的不完备性与不准确性、局中人利益的多元化与目标的多样性、知识经验与能力的局限性，局中人联盟的特征(或支付)函数通常用模糊值而非精确值来表示[1-4]。联盟特征函数用区间值表示的合作对策就是联盟值具有不确定性的合作对策的一种重要形式，常简称为区间值合作对策。在区间值合作对策中，往往无法确切地知道每个联盟的收益，而只能估计出联盟收益的模糊值，并且将其用一个闭区间的形式来表示。区间值合作对策是清晰(经典)合作对策的重要推广，近年来受到了一些研究者的关注，并逐渐被运用于解决一些竞争型经济管理决策问题[5-14]。比如，银行破产问题就是一个很好的区间值合作对策例子。Han Weibin等[5]介绍了区间值核心的概念和拟Shapley值，讨论了两者之间的关系并给出了可能存在的区间值解。Alparslan等[9]将经典的两人合作对策理论拓展到区间值两人合作对策，研究了核心、平衡性和超可加性等相关的概念。Li Dengfeng[13]给出了一种用于求解支付值用区间值来表示的矩阵对策的简单而高效的线性规划模型，并证明其是经典矩阵对策的拓展。

然而，现有区间值合作对策求解方法，大多数直接利用区间值减法等进行运算，极可能造成局中人收益(或分摊成本)的不确定性放大或为负值等问题。为此，本文借鉴最小平方法的思想，从任意联盟中的所有局中人都希望他们从最大联盟中获得的分配值之和至少能尽可能地接近其联盟值这一愿望为出发点(即局中人参与大联盟后所获得的分配值之和不应和他们单独形成联盟时获得的联盟收益偏离太多)，构造区间值距离公式，并建立以联盟分配与联盟支付之差的平方和为最小的数学优化模型，据此求解确定每个局中人的区间值分配，有效地避免了传统区间值合作对策求解过程中使用区间值减法带来的局中人区间值分配放大或分配所得为负值等不合理现象。

2 区间值运算与距离

2.1 区间值运算

用I(R)表示实数集R上所有有界闭区间集合。区间值a=[aL,aR]={x|x∈R,aL≤x≤aR}，其中aL∈R和aR∈R。显然，若aL=aR，则区间值a=[aL,aR]退化为一个精确数即实数，记为aL或aR。因此，区间值是精确数的拓展。换句话说，精确数是区间值的一种特殊情形。

区间值运算在区间值合作对策中具有重要作用。本小节介绍几种常见区间值运算法则[5,13-15]。

定义1 设a=[aL,aR]和b=[bL,bR]为I(R)上的两个区间值，γ∈R为任意实数。则：

(1)区间值相等：a=b当且仅当aL=bL和aR=bR。a=b意味着区间值a和b完全相同；

(2)区间值加法：a+b=[aL+bL,aR+bR]；

(3)区间值减法：a-b=[aL-bR,aR-bL]；

(4)区间值与实数的乘积：

2.2 区间值之间的距离

定义2设a=[aL,aR]、b=[bL,bR]和c=[cL,cR]是I(R)上的任意三个区间值。若满足下面三条条件：

(1)D(a,b)≥0；

(2)D(a,b)=D(b,a)；

(3)D(a,b)≤D(a,c)+D(c,b)，

则称D(a,b)为区间值a和b之间的距离。

为更好描述最小平方法思想在区间值合作对策中的应用，给出如下区间值距离(平方)公式：

D(a,b)=(aL-bL)2+(aR-bR)2

(1)

显然，式(1)满足定义2中条件(1)和(2)。下面仅证明条件(3)。事实上，根据式(1)，得：

D(a,b)=(aL-bL)2+(aR-bR)2≤[(aL-cL)2+(cL-bL)2]+[(aR-cR)2+(cR-bR)2]=[(aL-cL)2+(aR-cR)2]+[(cL-bL)2+(cR-bR)2]=D(a,c)+D(c,b)

即D(a,b)≤D(a,c)+D(c,b)。因此，式(1)为区间值a和b之间的距离。

3 求解区间值合作对策的最小平方优化模型

3.1 区间值合作对策

区间值合作对策υ定义在局中人集合N={1,2,…,n}上，区间值υ(S)为联盟S⊆N的联盟特征(或支付)值，也即区间值特征函数，记υ(S)=[υL(S),υR(S)]。规定υ(∅)=0，其中∅为空集。通常将υ({i})简写成为υ(i)(i∈N)。

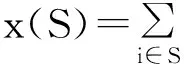
任意联盟S⊆N中的所有局中人都希望他们从最大联盟中获得的分配值之和尽可能地接近其联盟值υ(S)。利用式(1)，则区间值x(S)与υ(S)的差异可表示为如下的距离(平方)：

所有联盟S⊆N的距离之和可以表示为：

L(x)可看作为所有联盟的一种损失函数。

3.2 最小平方优化模型及其解法

容易看出，使损失函数L(x)取得最小值的解，可以得到所有局中人的一种最优分配方案，即区间值合作对策的一种解。为此，建立如下数学优化模型：

(2)

对L(x)关于变量xLj和xRj(j∈S⊆N)分别求偏导数，并令其等于0，即有：

从而可得：

(3)

(4)

为了求解xLi和xRi(i=1,2,…,n)，将方程组(3)和(4)分别展开，可得：

(5)

和

(6)

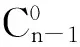
通过上述分析，可得：

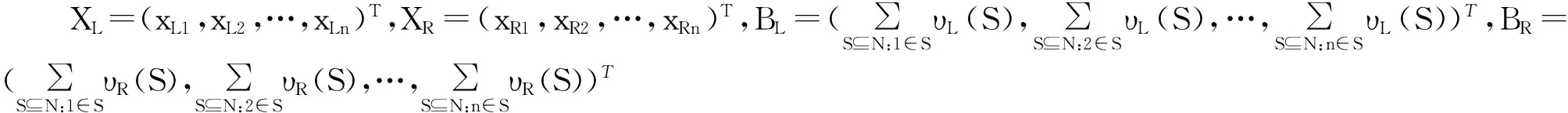
则方程(5)与(6)可分别写成如下矩阵形式：

AXL=BL

AXR=BR

记矩阵为：

其中E为单位矩阵。经过一系列初等行变化，可得：

(A,E)～

显然，矩阵A和E行等价，从而矩阵A可逆，且：

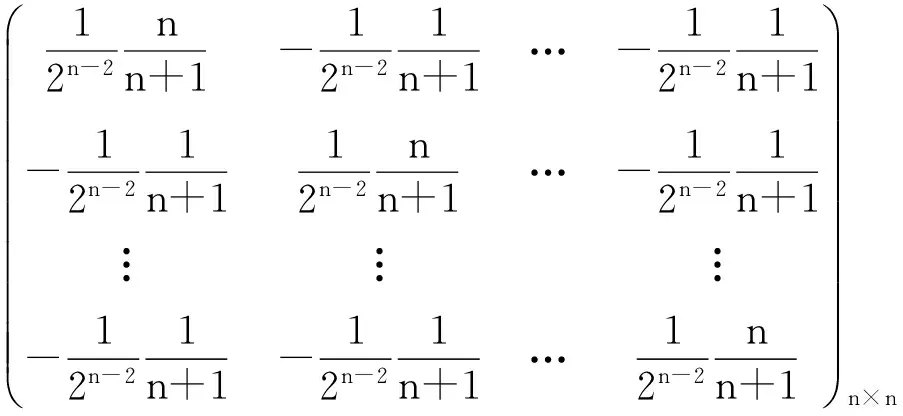
利用矩阵乘法，可得到方程(5)和(6)的解分别如下：

XL=A-1BL

(7)

XR=A-1BR

(8)

由此可以计算得到局中人i∈N的分配值，即区间值xi=[xLi,xRi](i=1,2,…,n)。

3.3 最小平方优化模型的拓展及其解法

有趣的是，在两次金融危机——1997年亚洲金融危机、2008年美国次贷危机之后世界各国的FD与kaopen指数均出现增速骤减，对于中低收入国家而言甚至出现了两个指标的负向变化。这一现象一方面说明金融危机对于不同发展阶段国家的影响可能是异质的，低收入国家由于经济规模、金融体系发展等相对滞后可能会承担更多的风险。另一方面也说明国家依据当前国际金融与国内金融环境审慎调整金融政策与金融开放政策是应对金融危机的当然举措。

在上述优化模型即式(2)中，可根据管理决策实际需要，增加一些约束条件，比如，集体合理性条件(或有效性)即x(N)=υ(N)。于是，由式(2)可容易地写出如下带有约束条件的数学优化模型：

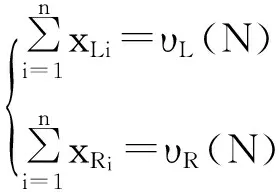
(9)

为了求解式(9)，构造如下拉格朗日函数：

其中λ和μ为拉格朗日乘子。

对L(x,λ,μ)分别关于变量xLj、xRj(j∈S⊆N)、λ和μ求偏导数，并令其等于0，可得：

和

从而可得：

(10)

和

(11)

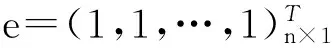
(12)

eTX′L=υL(N)

(13)

求解方程(12)，可得：

(14)

代入方程(13)，可得：

(15)

根据式(14)和(15)，可得到：

即，

(16)

用类似方法求解方程组(11)，可得：

(17)

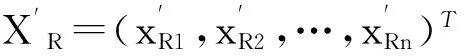
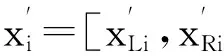
4 实例计算分析

4.1 案例背景及计算

假设有3家不同的快递企业(即局中人)1、2和3均要为某高校配送物品，由于受到市场环境、油价、人工成本、城市道路状况等多种因素的影响，快递企业无法提前预知确切的配送收益，只能预估出大致的收益范围，即配送所得的收益用闭区间来表示。若上述3家快递企业都选择单独对高校进行配送，其期望收益范围均为10至11万元，即υ(1)=υ(2)=υ(3)=[10,11]。若快递企业开展共同配送，则通过资源整合可以较大的提高收益，具体为：若快递企业1和2开展共同配送，则联盟{1,2}的收益为υ({1,2})=[28,32]；若快递企业1和3开展共同配送，则联盟{1,3}的收益为υ({1,3})=[30,38]；若快递企业2和3开展共同配送，则联盟{2,3}的收益为υ({2,3})=[25,28]；若3家快递企业一同合作开展共同配送，则收益可大大提高，即最大联盟N={1,2,3}的收益为υ({1,2,3})=[45,50]。

对于参与共同配送的3家快递企业来说，都不希望自己参加大联盟后所获得的收益比单干或彼此之间形成子联盟时获得的联盟收益少太多，这将降低甚至破坏他们参与大联盟的积极性；反之，参与大联盟的任何一家快递企业也绝不希望看到其他两家快递企业因为参与了大联盟，所分配得到的收益比其单干或形成子联盟时获得的联盟收益高太多，这也将影响其加入大联盟的积极性。为了平衡这种矛盾，我们希望看到每一家快递企业参与大联盟后获得的收益都与其单干或形成子联盟时获得的联盟收益尽可能的接近，这不失为一种公平、合理的利益分配方案。为此，利用公式(7)和(8)对大联盟获得的收益进行分配。

将上面的相关数据代入式(7)和(8)，可得：

即，快递企业(即局中人)1、2和3得到的分配值分别为：

x1=[xL1,xR1]=[15.1,18.1],x2=[xL2,xR2]=[12.6,13.1],x3=[xL3,xR3]=[13.6,16.1]。

因此，快递企业1从合作中可以期望得到的收益在15.1至18.1万元之间；快递企业2从合作中可以期望得到的收益在12.6至13.1万元之间；快递企业3从合作中可以期望得到的收益在13.6至16.1万元之间。显然，3家快递企业通过合作均可获得更多的收益。

若考虑集体合理性(即有效性)条件，则利用式(16)和(17)，可得：

于是，快递企业(即局中人)1、2和3所得的分配值分别为：

这样，快递企业1从合作中可以期望得到的收益在16.3至19.0万元之间；快递企业2从合作中可以期望得到的收益在13.8至14.0万元之间；快递企业3从合作中可以期望得到的收益在14.8至17.0万元之间。因此，3家快递企业通过合作均可获得更多的收益，且3家快递企业从最大联盟中分配得到的收益的上限之和与下限之和与最大联盟收益的上、下限分别相等，即所有的收益均分配完毕。

为验证本文所提出模型与方法的正确性及可靠性，用Lingo软件对上述实例进行求解，所得结果与利用式(7)和(8)(或式(16)和(17))求得的结果完全一致，有兴趣的读者可自行验证。

4.2 与现有方法的比较分析

(1)求解方法复杂性和计算量方面的优势。利用于晓辉等[16]中的方法，为求得各个局中人的收益分配，需要分别对每个局中人进行求解，工作量大、计算过程重复且繁琐；利用本文提出的方法，只需代入一次数据，即可同时得到最大联盟(或子联盟)中所有局中人的收益分配。

(2)应用范围方面的优势。利用于晓辉等[16]中的方法，局中人所得区间值收益的上限和下限之和分别为234/6和56，与最大联盟的区间值收益[45,50]相比有较大偏差，不满足集体合理性(或有效性)条件即x(N)=υ(N)；利用本文提出的方法(式(16)和(17))，局中人所得区间值收益的上限和下限之和分别为45和50，与最大联盟的区间值收益[45,50]的上、下限一致，即满足集体合理性(或有效性)，也即最大联盟的收益被完全充分地分配。换句话说，当参与合作的局中人不希望联盟在收益分配过程中出现“空头支票”或联盟收益还有剩余时，用本文提出的方法比于晓辉等[16]中方法更加合理。此外，由于于晓辉等[16]所提方法运用了区间值减法运算，当用区间值来表示的联盟特征值υ(S)=[υL(S),υR(S)](S⊆N)覆盖υ(Si)=[υL(Si),υR(Si)](i∈S,S⊆N)，即υL(Si)≤υL(S)≤υR(Si)时，极易出现局中人参加联盟后所分配得到的收益为负值或比单干时候获得的收益更少的情形，这显然不合理。在这种情况下，用本文所提方法进行合作收益的分配显得更为有效和实用。准确、具体地说，于晓辉等[16]的方法只适用于求解一类具有联盟大小单调性(SizeMonotonicity)的区间值合作对策[7]，即区间值联盟特征函数满足条件：υR(S)-υL(S)≥υR(Si)-υL(Si)(i∈S,S⊆N)，而本文方法适用于求解包括具有联盟大小单调性的区间值合作对策在内的任意区间值合作对策，即不要求区间值合作对策具有任何附加的约束条件。

(3)求解结果合理性方面的优势。利用于晓辉等[16]中的方法，局中人所得区间值收益的范围最大为6.2，且均大于5；利用本文提出的方法，局中人所得区间值收益的范围最大为3，最小为0.2，有效地降低了分配结果的不确定性。

5 结语

针对区间值合作对策问题，本文利用最小平方法和区间值距离概念，构建最小平方优化模型，并导出局中人区间值分配值的解析公式。文中方法原理简单、计算量小，并且由于计算过程中未直接使用区间值的减法运算，可有效地避免区间值减法带来的局中人分配值不确定性放大以及局中人分配值可能为负值等不合理问题，可为区间值合作对策问题提供一种新的有效解决途径，有望在更多的经济、社会、管理等领域得到广泛应用。

然而，从实例计算结果可以看出，利用式(9)求得的局中人分配结果虽然满足集体合理性条件，但却没有完全满足联盟合理性条件。比如，厂商(即局中人)1与3最终获得的区间值分配值(即收益)的上界之和(36万元)小于他们组成联盟{1,3}时获得的区间值联盟值的上界(38万元)，导致厂商1与3组成的联盟{1,3}会有分裂的动机，从而影响最大联盟的稳定性。当然，这样的问题在Branzei等[3,6]，Han Weibin[5],Alparslan等[7]，Mallozzi等[8]和于晓辉等[16]类似方法中同样存在。因此，能否像核心(Core)一样，在式(2)(或式(9))中同时考虑个体合理性、联盟合理性和集体合理性等约束条件，并导出类似于式(7)和(8)(或式(16)和(17))的局中人分配值(解析公式)将是今后研究的一个重要内容。

[1] 李登峰.模糊多目标多人决策与对策[M].北京:国防工业出版社,2003.

[2] Li Dengfeng. Lexicographic method for matrix games with payoffs of triangular fuzzy numbers[J]. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2008, 16(3): 371-389.

[3] Branzei R, Branzei O, Alparslan Gök S Z, et al. Cooperative interval games: A survey[J]. Central European Journal of Operations Research, 2010, 18(3): 397-411.

[4] 李登峰.直觉模糊集决策与对策分析方法[M].北京:国防工业出版社,2012.

[5] Han Weibin, Sun Hao, Xu Genjiu. A new approach of cooperative interval games: The interval core and Shapley value revisited[J]. Operations Research Letters, 2012, 40(6): 462-468.

[6] Branzei R, Dimitrov D, Tijs S. Shapley- like values for interval bankruptcy games[J]. Economics Bulletin, 2003, 3(8): 1-8.

[7] Alparslan Gök S Z, Branzei R, Tijs S. The interval Shapley value: An axiomaticzation[J]. Central European Journal of Operations Research, 2010, 18(2): 131-140.

[8] Mallozzi L, Scalzo V, Tijs S. Fuzzy interval cooperative games[J]. Fuzzy Sets and Systems, 2011, 165(1): 98-105.

[9] Alparslan Gök S Z, Miquel S, Tijs S. Cooperation under interval uncertainty [J]. Mathematical Methods of Operational Research, 2009, 69(1): 99-109.

[10] Branzei R, Alparslan Gök S Z, Branzei O. Cooperation games under interval uncertainty: On the convexity of the interval undominated cores[J]. Central European Journal of Operations Research, 2011, 19(4): 523-532.

[11] Yu Xiaohui, Zhang Qiang. An extension of cooperative fuzzy games[J]. Fuzzy Sets and Systems, 2010, 161(11): 1614-1634.

[12] Alparslan Gök S Z, Branzei O, Branzei R, et al. Set-valued solution concepts using interval-type payoffs for interval games[J]. Journal of Mathematical Econo- mics, 2011, 47(4-5): 621-626.

[13] Li Dengfeng. Linear programming approach to solve interval-valued matrix games[J]. Omega, 2011, 39(6): 655-666.

[14] Li Dengfeng. Models and methods of interval-valued cooperative games in economic management[M].Switzerland:Springer, 2014.

[15] Moore R E. Methods and applications of interval analysis[M]. SIAM: Studies for Industrial and Applied Mathematics, 1979.

[16] 于晓辉,张强.模糊合作对策的区间Shapley值[J].中国管理科学,2007,(Z1):76-80.

Models and Method of Interval-valued Cooperative Games Based on the Least Square Distance

LI Deng-feng1， LIU Jia-cai1,2

(1.School of Economics and Management, Fuzhou University, Fuzhou 350108, China；2.School of Traffic and Civil Engineering, Fujian Agriculture and Forestry University, Fuzhou 350002, China)

interval-valued cooperative game; least square method; loss function; dispatch coalition; mathematical programming

1003-207(2016)07-0135-08

10.16381/j.cnki.issn1003-207x.2016.07.016

2014-12-24；

2015-10-20

国家自然科学基金重点项目(71231003)；国家自然科学基金资助项目(71171055)；高等学校博士学科点专项科研基金资助课题(20113514110009)；福建省社会科学规划项目(2013C024)；福建省教育厅科技项目(JA13122)

李登峰(1965-)，男(汉族)，广西博白人，福州大学经济与管理学院教授，博导，研究方向：经济管理决策与对策(博弈),E-mail:lidengfeng@fzu.edu.cn.

O

A