中小企业信用再担保体系演化稳定条件分析

汪 辉，邓晓梅，杨伟华，冯 珂

(1.清华大学建设管理系，北京 100084；2.军事经济学院军队财务系，湖北 武汉 430035)

中小企业信用再担保体系演化稳定条件分析

汪 辉1，2，邓晓梅1，杨伟华2，冯 珂1

(1.清华大学建设管理系，北京 100084；2.军事经济学院军队财务系，湖北 武汉 430035)

为研究非强制性再保情况下，中小企业信用再担保体系稳定发展应具备的条件，本文建立中小企业信用担保与再担保机构行为策略的演化博弈模型，利用微分方程稳定性原理求解演化稳定策略，并确定再担保体系稳定发展所需的条件；以此为基础，在保证再担保体系稳定发展的前提下，定量描述了担保和再担保机构之间的风险分担比例、再担保保费、最低政府风险补贴要求等再担保运营机制具有的可调节范围；最后，结合算例进行验证和应用分析。研究发现：1)若担保机构加入再担保体系后，同时满足再担保机构增加的收益为正、担保机构增加的收益大于申请成本，则可保证再担保体系稳定发展；2)代偿率对再担保运营机制的可调节范围有重要影响，代偿率越高，风险分担比例、再担保保费具有的可调节空间越小，若随代偿率上升不存在调节空间时，需要政府对担保、再担保机构进行适当的风险补贴，以保证再担保体系稳定发展。这些研究结果为我国中小企业信用再担保的实践提供了理论参考。

中小企业信用再担保；演化稳定条件；可调节范围

1 引言

中小企业信用再担保是中小企业信用担保体系的拓展和延伸，指以国家政策为导向，通过再担保合约，由再担保机构为中小企业信用担保(以下简称“担保”)机构提供一定比例的再担保责任，实现为担保机构增信和分散风险的一种制度安排[1-4]。不同于一般的信用再担保，中小企业信用再担保(以下简称“再担保”)不以盈利为目的，通常可获得政策扶持，如财政资金支持、税收优惠、贴息贷款等，同时担保、再担保保费确定也要体现政策特点。

目前，具有稳定中小企业信用再担保体系的国家主要有日本、韩国、德国等。在这些国家，依据相关法律，担保机构将被自动纳入再担保体系，每笔担保业务实行自动再担保[5]。结合我国的特点，中小企业信用再担保体系建设应坚持“政策性引导、公司化管理、市场化运作”的模式[2-4]，并未将担保机构自动纳入再担保体系，这意味着再担保机构需要通过市场机制建立与担保机构之间的再担保关系。在非强制性自动再保的市场条件下，担保和再担保机构是直接的被担保人和担保人，他们的行为策略对再担保体系的稳定发展有着重要的直接影响。那么，通过市场化手段吸引担保机构选择加入再担保体系，进而形成稳定的再担保体系应具备什么条件？在保证再担保体系稳定发展的前提下，担保与再担保机构之间的风险分担、再担保保费具有多大的可调整空间？最低政府补贴应满足什么要求？这些都是当前我国再担保体系发展中迫切需要解决的问题。

目前，国外学者主要围绕中小企业信用担保展开研究，内容涉及面广，如担保资金压力测试[6]、担保体系内中小企业违约概率预测[7]、担保保费估计[8]、担保政策效果评估[9]等等，但较少涉及再担保的内容。国内关于再担保的文献除再担保模式方面的研究外，主要聚焦于以下三个方面。一是关于再担保体系中风险分担和再担保保费问题的研究：于孝建和徐维军[10]采用数理模型分析方法，通过分析各合作方的风险和收益，确定最优风险分担比例；薛钰显和王东超[11]利用讨价还价博弈模型分析了担保、再担保机构之间风险比例确定的方法，认为风险分担比例应由担保、再担保机构的消耗系数及保费确定。二是关于政府补贴问题的研究：林平和袁中红[12]通过对广东省信用担保机构的全面考察，建议应建立基于再担保的风险补偿机制和财政弥补机制；蔡文宇和陈玉菁[13]通过静态博弈分析，认为中小企业信用担保体系引入政府补贴有助于增强担保市场的有效需求和供给；财科所[14]分析了财政支持中小企业信用担保的必要性、可行性，在借鉴国外成功经验做法基础上，针对我国当前担保体系中存在的问题，提出应该建立财政资金支持担保体系的长效机制、促进财政支持路径的集中化和系统化；冯涛等[15]通过建立数理模型对不同的财政资助方式进行比较分析，认为通过再担保机构对担保体系进行风险补贴是最优选择。三是关于再担保体系中各方经济效益的研究：如马国建等[16]、梅强等[17]利用仿真手段研究了再担保体系中各方的经济效益。

这些成果为再担保实践起到了一定的指导作用，但都以完全理性人假设为基础，与现实存在一定差距；也未考虑再担保体系发展的稳定性问题，更未涉及在确保再担保体系稳定发展的前提下，不同再担保运营机制所具有的动态调节空间。

实际上，在非强制性自动再保的市场条件下，再担保系统的发展过程是担保与再担保机构之间不断博弈的过程，由于未来的不确定性，不可能通过一次博弈就达到均衡状态，需要从动态的角度，探寻双方博弈行为策略的调整过程、演化趋势和稳定性条件。因此，面对未来的不确定性，参与博弈的担保、再担保机构更符合有限理性的假设，可自由确定自身的行为策略，通过不断地模仿学习，从各自的策略集合中选择较优策略，以提高环境适应能力。

演化博弈理论是从系统论出发，以有限理性为基础，通过“复制动态”、“最优反应动态”等学习调整机制描述群体模仿学习、调整策略的演化博弈过程[18]。其中，复制动态适合描述大群体、学习速度较慢的演化博弈过程，即，每种策略在当前阶段的收益将决定下一阶段采取该策略的参与者数量在群体中所占的比例，经过长期的重复，采取较高收益策略的参与者数量在群体中的比例将会越来越高，而采取较低收益策略的群体比例会越来越低，直至最后消亡[19]。与传统博弈理论相比，演化博弈以有限理性假设为前提，更加贴近现实，在经济、社会、环境等相关领域得到了广泛应用[20-22]。

因此，在再担保系统中，将具有一定数量的担保和再担保机构看成两个不同的群体，由于这两类群体都是集体决策，不同机构之间存在信息不对称，他们从认知不足到策略调整的反馈过程较慢，利用复制动态来研究他们策略选择的互动机制，探索形成稳定再担保体系所应满足的条件，将更加贴近实际。

与已有研究不同，本文将运用演化博弈理论，假设担保、再担保机构属于有限理性人，构建担保和再担保机构的行为策略演化博弈模型；然后利用微分方程稳定性原理寻找系统的演化稳定策略(ESS，Evolutionary Stable Strategy)及其条件，进而确定通过市场化手段形成稳定再担保体系应具备的条件；在保证再担保体系稳定发展的前提下，进一步分析担保与再担保机构之间的风险分担、再担保保费以及最低政府补贴要求等再担保运营机制具有的可调节空间，为再担保运营机制的动态调整提供理论参考。

2 担保-再担保行为策略的演化博弈模型

2.1 系统背景与基本假设

(1)担保、再担保机构符合有限理性人假设。这意味着担保、再担保机构面对未来的不确定性，难以在一次事件中做出最优决策，需要通过模仿学习较优策略，改进自身的行为。

(2)假设担保机构的授信额度每年都可以全部用完。当前普遍现象是担保机构因授信不足，难以满足中小企业的信贷需求，故此假设符合实际。

(3)假设担保、再担保机构为了获取更多收益而调整自身的行为策略。尽管中小企业信用担保的宗旨是为解决中小企业的融资困境，担保、再担保机构不应以追求盈利为首要目标，但追求适当的收益也是必要的，否则因不断亏损而倒闭，就谈不上扶持中小企业了。

(4)假设政府通过再担保体系对担保机构进行风险补贴，未加入再担保体系的担保机构不能得到政府的风险补贴。目前我国已基本形成由政策性担保、互助担保和商业担保并存的担保体系，但并未形成统一的补贴形式，其中，政策性担保机构可获得较为稳定的政府补贴，而其他担保机构却较难享受政府的资助[14]。但非政策性担保机构却占有较大比重，据融资性担保业务监管部际联席会议办公室公布的数据，截至2011年，全国融资性担保公司共8402家，其中民营及外资控股占81.3%。根据已有研究成果，本文假设通过再担保机构向担保机构进行风险补贴符合发展方向，不考虑对未加入再担保体系的担保机构进行财政风险补贴符合当前客观现实。

(5)假设经过考察筛选加入再担保体系的担保机构会继续保持良好的运营状态，若因落实中小企业信用担保政策出现收支缺口，可及时得到政府的风险补贴，不至出现亏损，此假设与财政支持中小企业信用担保体系发展的宗旨一致[14]。

记担保机构自有资金为K，银行对其放大倍数为n，保费费率为g1(以担保金额为基数)，对被担保人的平均调查监控成本为V1(以担保金额为基数)，年平均代偿率为ω，代偿后反担保物变现占代偿金额的比例为C，申请加入再担保体系的成本为F1，加入再担保体系后，应付的再担保费率为g2(以担保保费为基数)，承担的风险比例为λ；再担保机构考察担保机构的成本为F2，对加入体系的担保机构平均监控成本为V2(以分担的再担保金额为基数)。政府对再担保机构的补贴为代偿金额的a倍，a∈[0,1]，通过再担保机构对担保机构的补贴为代偿金额的b倍，b∈[0,1]。

在再担保系统中，对于担保机构，可选择的策略集合为A={A1,A2}，其中A1表示申请加入再担保体系，A2表示不申请加入；而再担保机构可选择的策略集合为B={B1,B2}，其中B1表示再担保机构接受担保机构的申请，B2表示不接受申请，则可建立担保、再担保机构博弈的支付矩阵，如表1所示。

表1 担保、再担保机构博弈的支付矩阵

2.2 演化博弈模型的构建

假设担保机构采取A1策略的比例为p，采取A2策略的比例为(1-p)；再担保机构采取B1策略的比例为q，则采取B2策略的比例为(1-q)。则担保机构，采取A1策略的期望收益为E1，采取A2策略的收益为E2，如式(1)、(2)所示：

(1)

E2=nKg1-ωnK(1-C)-V1nK

(2)

则担保机构的平均期望收益E为：

E=pE1+(1-p)E2

(3)

依据Malthusian动态方程[23]，担保机构采取A1策略的复制动态方程为：

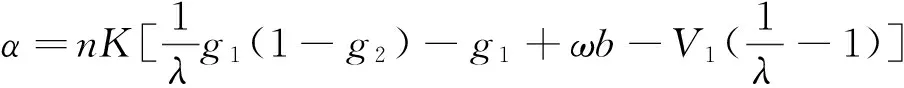
(4)

同理，再担保机构采取B1策略的收益D1，采取B2策略的收益为D2，平均期望收益D及采取B1策略的复制动态方程G(q)分别如式(5)～(8)所示:

(5)

D2=-pF2

(6)

D=qD1+(1-q)D2

(7)

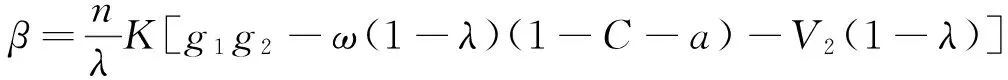
(8)

则担保、再担保机构的演化博弈系统可由(4)、(8)式组成的微分方程组进行描述，即：

(9)

其中，p∈[0,1]，q∈[0,1]。

3 再担保体系演化稳定条件分析

3.1 担保机构策略选择的演化博弈分析

根据(4)式，当q=q*=F1/α(即，再担保机构选择接受担保机构加入策略的比例，与担保机构加入再担保体系后单位增加收益的申请成本相等)时，p取任何值均为稳定状态。当q≠q*时，担保机构的策略选择将与q值有关，下面根据微分方程稳定性原理分析在此情况下担保机构的演化稳定策略。

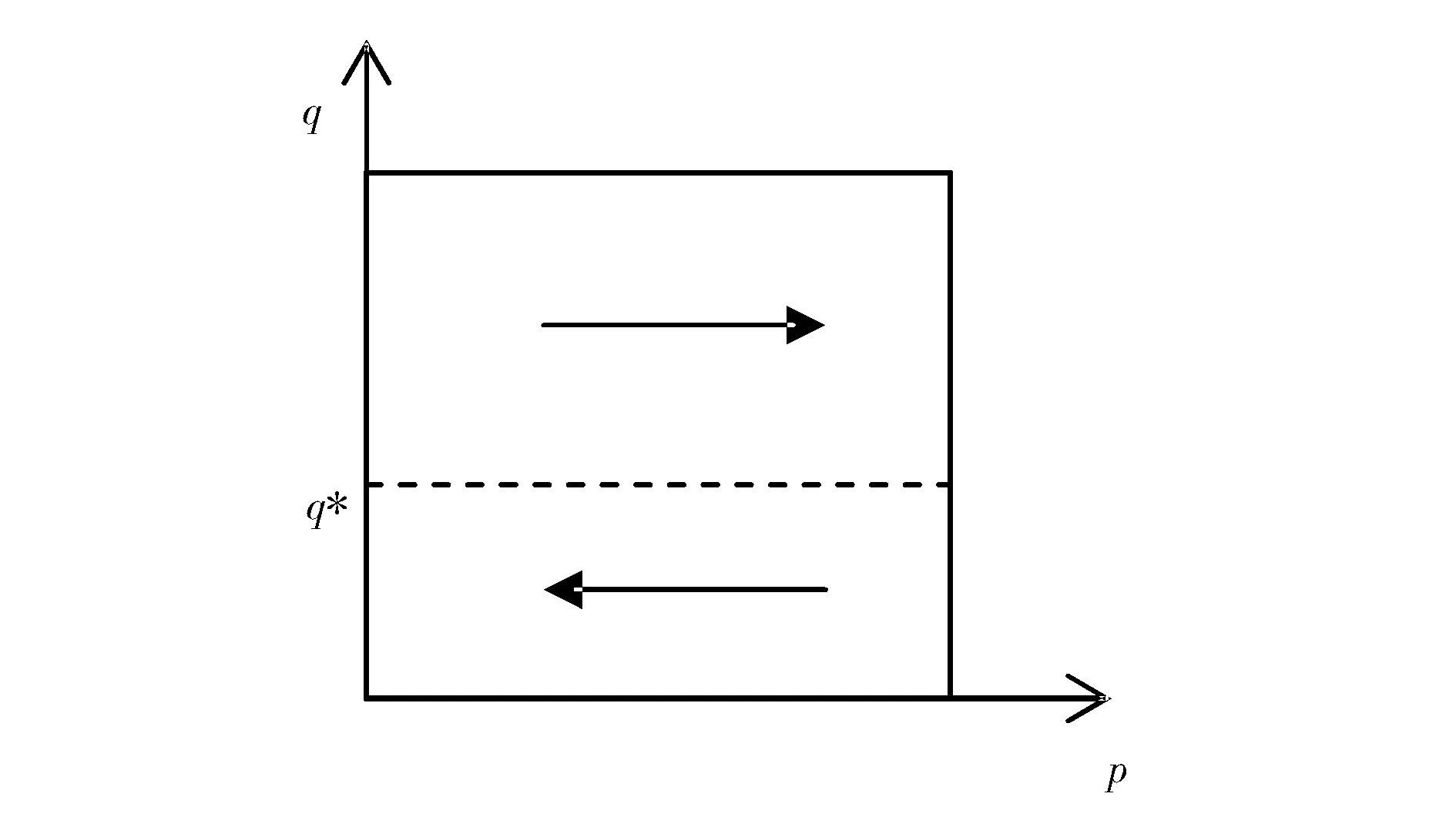
图1 α>0时担保机构系统的演化路径

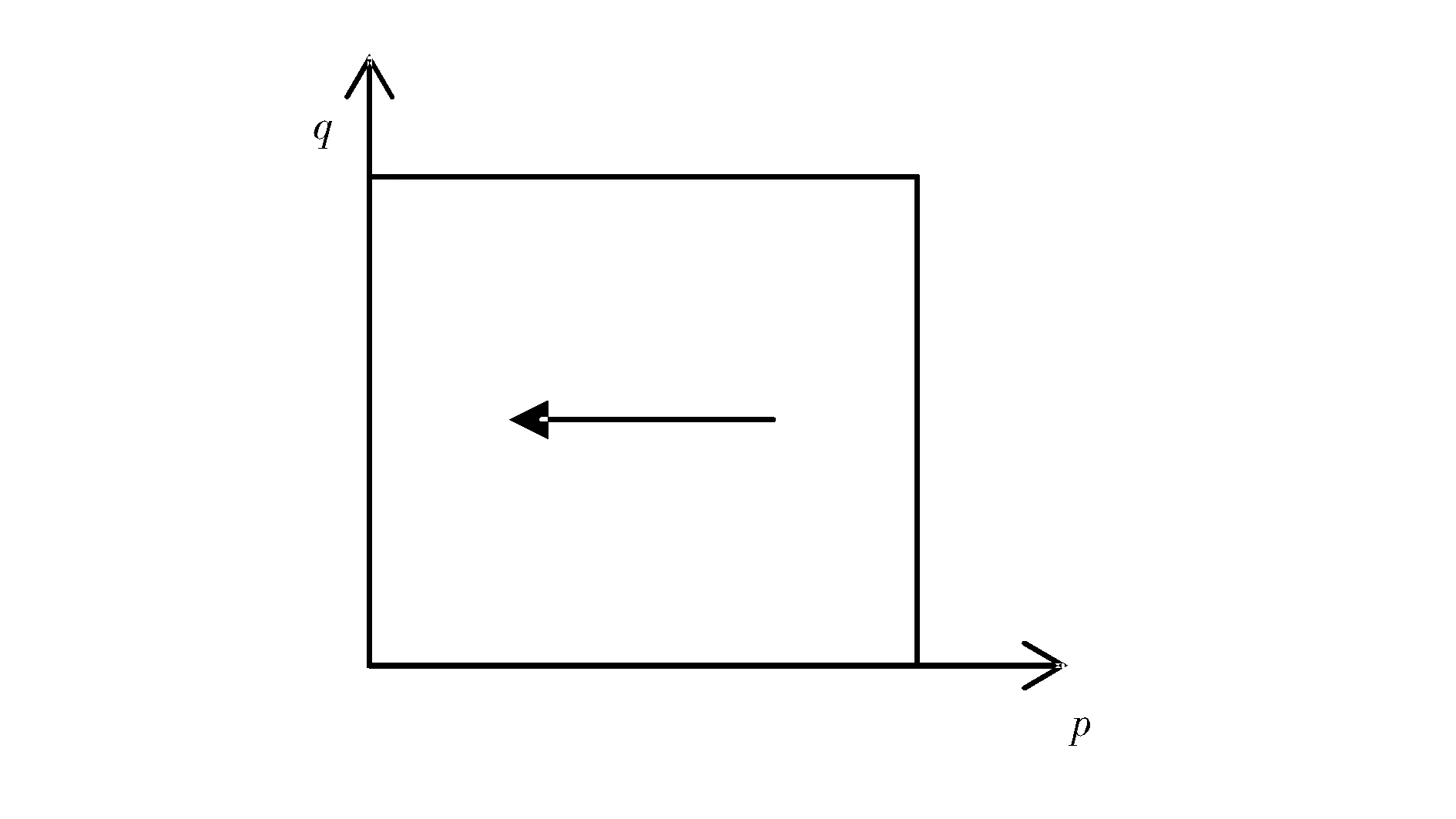
图2 α<0时担保机构系统的演化路径

3.2 再担保机构策略选择的演化博弈分析

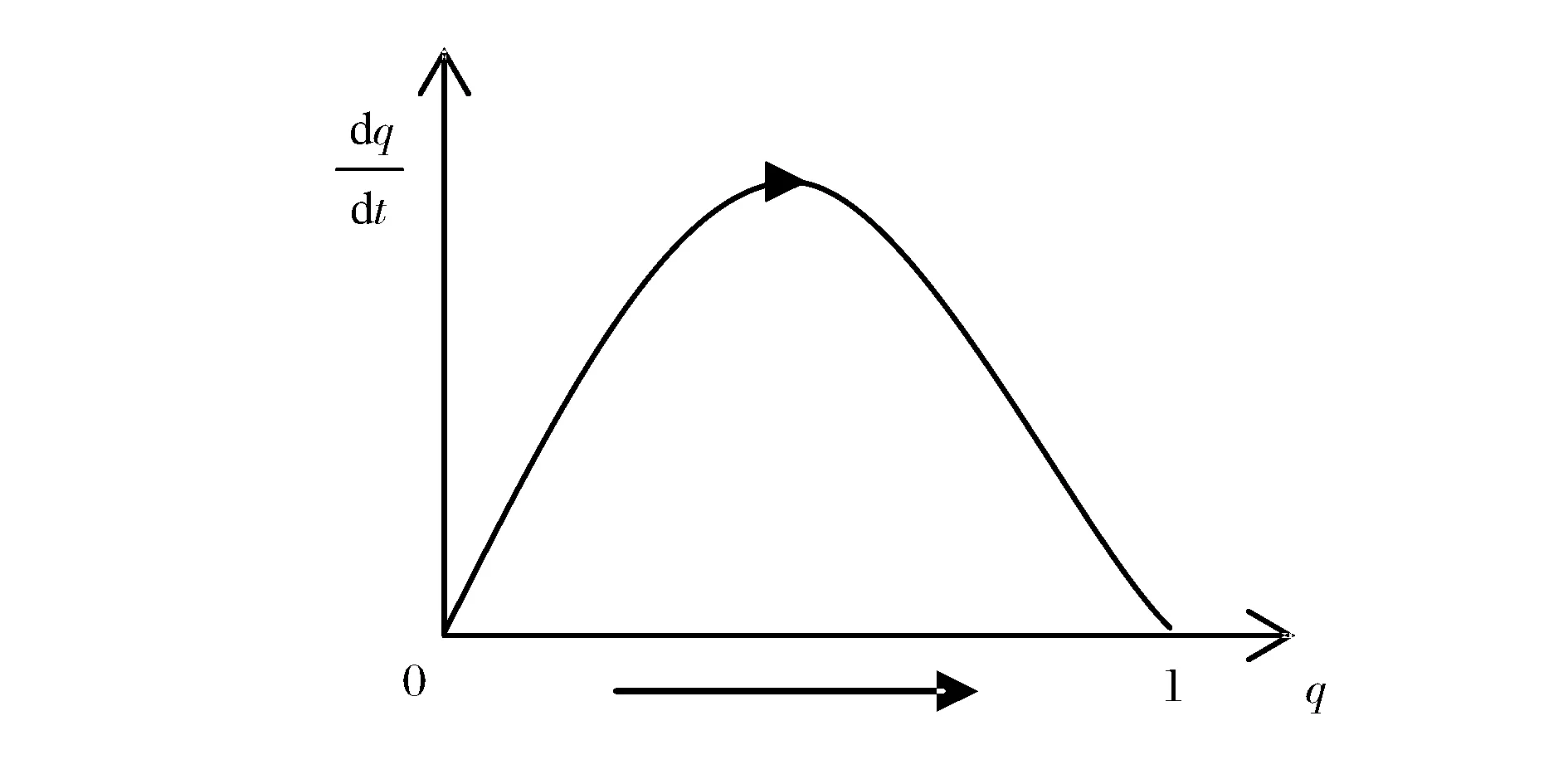
图3 β>0时再担保机构策略的演化路径

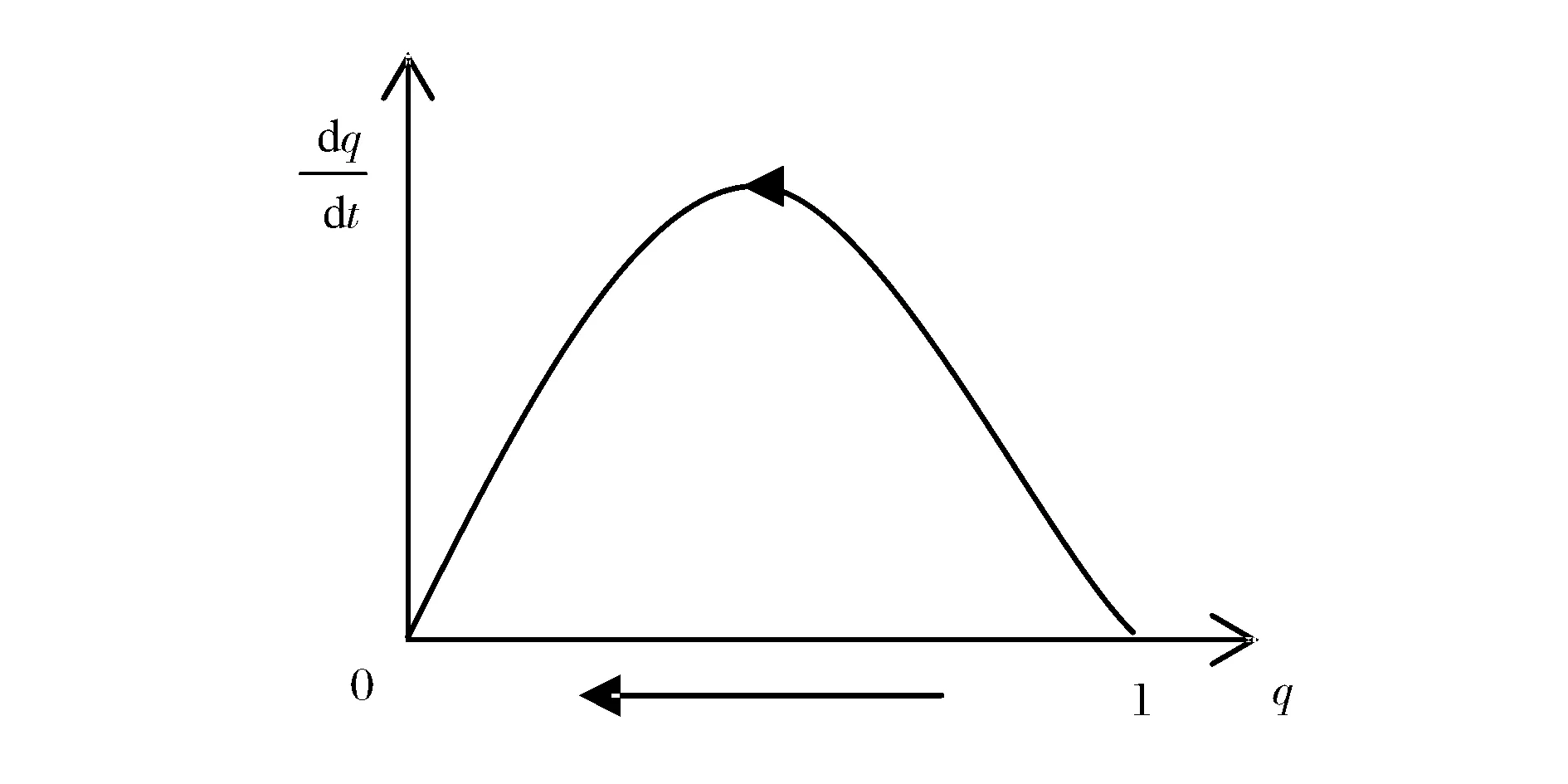
图4 β<0时再担保机构策略的演化路径

3.3 再担保系统的演化稳定性分析

根据担保和再担保机构策略选择的演化博弈系统对应的微分方程组(9)，可得其对应的雅克比矩阵J、行列式Det(J)、迹Tr(J)如式(10)、(11)、(12)所示：

(10)

Det(J)=(1-2p)(αp-F1)×βp(1-2q)-αβpq(1-p)(1-q)

(11)

Tr(J)=(1-2p)(αq-F1)+βp(1-2q)

(12)

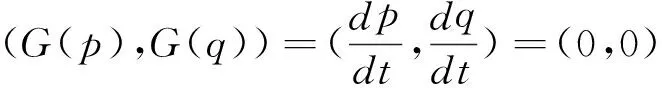
进一步利用雅克比矩阵局部稳定性分析法[24]和中心流形定理[25]对该微分方程组系统进行演化稳定性分析，结果如表2所示。

表2 均衡点的演化稳定性分析

根据表2的结果可知，共有三种可能的演化稳定策略(ESS)：

(1)当担保机构加入再担保体系后增加的收益α大于申请成本F1，接受担保机构加入的再担保机构初始比例q小于担保机构加入再担保体系后单位增加收益的申请成本F1/α，并且，接受担保机构加入再担保体系后再担保机构增加的收益β为负；或者担保机构加入再担保体系后增加的收益α、接受担保机构加入再担保体系后再担保机构增加的收益β均为负时，担保机构将选择“不申请加入”再担保体系、再担保机构将选择“不接受”加入，再担保体系将随着时间的流逝，最终消亡。

(2)当担保机构加入再担保体系后增加的收益α为负，而接受担保机构加入再担保体系后再担保机构增加的收益β为正时，担保机构将选择“不申请加入”再担保体系、再担保机构将选择“接受”加入，再担保体系将随着时间的流逝也会逐渐消亡。

(3)当担保机构加入再担保体系后增加的收益α大于申请成本F1，并且接受担保机构加入再担保体系后再担保机构增加的收益β为正时，担保机构将选择“申请加入”再担保体系、再担保机构将选择“接受”加入，最后会形成稳定的再担保体系。

因此，通过担保、再担保机构策略选择的演化分析可知，要使策略组合：担保机构将选择“申请加入”再担保体系、再担保机构选择“接受”加入，成为系统的演化稳定策略，必须满足：再担保机构接受担保机构加入再担保体系后增加的收益β为正，并且，担保机构加入再担保体系后增加的收益α大于申请成本F1。这正是在非强制性自动再担保的市场条件下，再担保体系能够稳定演化发展所应具备的条件。当然这些条件，都以本文基本假设为前提。

4 再担保体系不同运营机制可调整范围分析

若要保证再担保体系可持续稳定发展，必须保证β>0且α-F1>0。同时，根据本文的基本假设(5)，政府的风险补贴可及时弥补再担保体系中担保机构的收支缺口，再担保机构接受担保机构加入再担保体系后，担保机构的收益不为负。也即：

在保证再担保体系稳定发展的基础上，据(13)～(15)式可进一步分析风险分担比例、再担保保费的可调整空间，以及最低政府补贴要求，为再担保体系不同运营机制的动态调整提供参考。

4.1 风险分担比例的可调整范围

在再担保体系中，如担保机构自身承担的风险比例过高，则再担保体系增信、分险的作用难以发挥；若再担保机构分担的风险过高也会导致其入不敷出，难以实现可持续发展。为保证再担保体系的可持续稳定发展，依据(13)～(15)式，担保机构承担的风险比例λ必须同时满足如(16)、(17)、(18)式的关系：

(19)

对于(17)式，同样地，政府给予再担保机构的风险补贴也不可能大于实际代偿金额，故ω(1-C-a)≥0，而且监控成本V2>0，则有：

(20)

综合以上分析，在确保再担保体系可持续稳定发展的条件下，担保机构承担的风险比例λ应满足：

(21)

担保机构风险比例λ的下限由(17)式转化而来，说明担保机构的最小风险分担比例由再担保机构增加的收益β是否为正所控制；而上限由(16)、(18)式转化而来，意味着担保机构的最大风险分担比例由其加入再担保体系后自身的收益是否为正、以及增加的收益α是否大于申请成本F1共同决定，也即，担保机构的最小风险分担比例由外界因素决定，而最大风险分担比例由自身因素决定，符合客观现实。特别地，在其它量不变的情况下，代偿率ω越高，λ的下限会增大，而上限需要进行比较才能确定。当代偿率上升至一定程度，λ可调整的空间将不存在，意味着再担保体系单靠调整担保机构承担的风险比例难以维持稳定，需要采取其它措施。

4.2 再担保费率的可调整范围

再担保保费应根据代偿风险、再担保机构所承担的风险比例等因素确定，但由于代偿风险的不确定性，再担保保费通常只能依据历史数据进行估计，因此在保证再担保体系稳定发展的条件下，讨论再担保费率的可调节范围，对再担保体系运营机制的动态调整也同样具有很强的现实意义。依据(13)～(15)式，再担保费率应满足如下关系：

由于n、K、g1>0，且0<λ<1，故再担保费率g2可调整的范围如(25)式所示：

(25)

类似地，再担保最低费率据(23)式转化而来，由再担保机构自身因素决定——增加的收益β是否为正；而最高费率据(22)、(24)式转化而来，受外界因素控制，由加入再担保体系的担保机构收益是否为正、以及其增加的收益α是否大于申请成本F1共同决定。特别地，在其它量不变的情况下，代偿率ω越高，再担保费率g2的下限将会增大，而上限需要经过比较才能确定；当代偿率上升至一定水平后，g2的可调整空间将不复存在，说明此时仅仅通过调节再担保保费无法保证再担保体系的稳定发展，需要采取其它措施。

4.3 最低的政府风险补贴

依据(13)～(15)式，为保证再担保体系的稳定发展，政府对再担保、担保机构的补贴应该满足如下关系：

由于ω、n、K>0，且0<λ<1，故政府对再担保机构的补贴应满足：

(29)

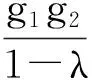
对担保机构的风险补贴应满足：

(30)

政府对担保机构的风险补贴下限由据(26)、(28)式转化而来，意味着最低风险补贴由担保机构收益是否为正、以及其增加的收益α是否大于申请成本F1共同决定。

政府风险补贴是再担保体系稳定发展的最后保障，当担保和再担保的风险分担比例、再担保保费等运营机制可调整空间不存在时，可根据当期的代偿情况，参考(29)、(30)式的最低补偿力度，形成动态的政府补偿机制。

5 算例分析

为更加直观展示再担保体系的演化博弈过程，验证建立稳定再担保体系应具备的条件是否正确，展现不同再担保运营机制的动态调整范围，下面结合具体算例进行应用分析。

以当前银行与担保机构合作的框架为基础，并参考文献[16-17]、融资性担保业务监管部际联席会议公布的2012年行业数据、中国融资担保协会整理的相关数据、工信厅联企业﹝2014﹞65号文件及对部分担保、再担保机构调研的数据，假设演化博弈开始时刻，模型中涉及变量的赋值分别为：担保机构自有资金K=10000万元，银行对担保机构的放大倍数n=4，担保机构保费费率g1=2%，担保机构对被担保人的平均调查监控成本V1=0.6%，年平均赔付概率ω=2%，反担保物变现占代偿金额的比例C=60%，担保机构申请加入再担保体系的成本F1=0.5万元，再担保机构考察担保机构的成本F2=0.5万元，担保机构加入再担保体系后承担的风险比例λ=50%，再担保费率g2=30%，再担保机构对担保机构的平均监控成本V2=0.2%，政府对再担保机构的风险补贴a=0，对担保机构的风险补贴b=0，则担保、再担保机构的收益矩阵如表3所示，并假设在博弈开始时，至少有一家担保机构申请加入再担保体系，即p≠0，再担保机构也不会拒绝所有的担保机构加入，即q≠0。

表3 担保、再担保机构的收益矩阵

5.1 再担保体系演化稳定性分析

根据各变量的赋值，可得β=80>0，α-F1=80-0.5=79.5>0，满足非强制性自动再保市场稳定演化的条件，故此时再担保体系经过演化，最终可以形成稳定系统。下面进一步验证再担保体系稳定演化条件的正确性。

根据(9)式，可知描述该系统演化过程的微分方程组为：

利用maple软件绘制该系统的相位图，如图5所示。从图5可知，该系统随时间流逝，最终收敛于p=1、q=1，说明它是系统的演化稳定策略，也即，通过不断的博弈和模仿学习，担保机构最终都会选择“申请加入”再担保体系、再担保机构将选择“接受”加入。该结论与依据再担保市场稳定演化条件判断的结果相同，说明再担保体系稳定演化条件是正确的。

图5 再担保系统演化的相位图

5.2 不同再担保运营机制的可调整范围

(1)风险分担比例的可调整区间

依据(21)式，可得担保机构承担的风险比例λ可调整的范围为：

40%<λ

演化过程中，代偿率ω变化时，λ的变化范围如表4所示。

表4 λ随代偿率变化时的取值范围

注：表中方框内数据是根据上、下限表达式计算的结果，但该可调整范围并不存在。

从表4可知，在其它量不变时，随代偿率的上升，担保机构风险分担比例λ的下限将增大，说明当代偿率上升，适当提高担保机构承担的风险比例，可保持再担保系统稳定发展。其上限此时受条件α-F1>0所控制，而b=0，故其上限并不随代偿率变化。当代偿率上升到一定程度，如ω=3%时，λ的可调整区间将不存在，这意味着系统将不会稳定发展。若要保证再担保体系继续稳定发展，必须采取其他的措施，如增加政府对担保、再担保机构的风险补贴，适当提高担保保费等。

(2)再担保费率的可调整范围

据(25)式，再担保费率g2的可调整区间为：

25%

演化过程中，代偿率ω变化时，g2的变化范围如表5所示。

表5 g2随代偿率变化时的取值范围

注：表中方框内数据是根据上、下限表达式计算的结果，但该可调整范围并不存在。

从表5可知，在其它量不变时，随代偿率的上升，再担保费率g2的下限将增加，说明当代偿率上升时，再担保机构可适当提高再担保费率，以保证系统稳定发展；其上限受条件α-F1>0所控制，而b=0，故上限并不随代偿率变化。当代偿率增大到一定程度，如ω=3%时，再担保费率g2的调整区间将不存在，意味着再担保体系将不能继续稳定发展，同样需要采取其它措施，如增加政府对再担保机构的风险补贴，降低再担保机构的风险分担比例，适当提高担保费率等。

(3)最低政府风险补贴要求

据(29)式，可得：

a>-10%，即取a=0

故在其它量不变时，政府无需对再担保机构进行补贴，再担保体系能够稳定发展。

据(30)式，可得：

b>max(-39.9%,-9.9%)，即取b=0

说明在其它量不变时，政府无需对担保机构进行补贴，再担保体系也可稳定发展。

演化过程中，代偿率ω变化时，政府对担保、再担保机构的最低风险补贴变化走势如表6所示。

表6 a、b随代偿率变化时的取值范围

从表6可知，在其它量不变时，随代偿率的上升，为保证再担保体系的稳定发展，政府需要再担保机构进行风险补贴；当代偿率上升到一定程度，不仅需要对再担保机构进行补贴，同时还需对担保机构进行补贴；当代偿率较低，如ω≤2%，担保、再担保机构在没有政府补贴的情况下，再担保体系也能稳定发展。

6 结语

本文假设担保、再担保机构为有限理性人，在非强制性再保的市场条件下，利用演化博弈理论分析了担保、再担保机构行为策略的演化博弈过程，根据演化稳定策略的形成条件确定了形成稳定再担保体系应具备的条件；同时，在保证再担保体系稳定发展的前提下，讨论了不同再担保运营机制所具有的可调整空间。主要得出如下结论：(1)在政府风险补贴能够及时弥补信用担保机构亏损的假设前提下，若接受担保机构加入再担保体系后再担保机构增加的收益为正，并且担保机构加入再担保体系后增加的收益大于申请成本，则可保证再担保体系稳定发展；(2)代偿率对再担保运营机制的可调整范围有重要影响，代偿率越高，风险分担比例、再担保保费具有的可调节范围越小，若随代偿率上升不存在调节范围时，需要对担保、再担保机构进行适当的风险补贴，以保证再担保体系稳定发展。

受当前信用担保理论和相应数据体系建设的限制，本文仅研究了担保、再担保机构具有确定性收益的演化博弈过程。实际上，处于不同时点，因代偿率的不确定性，担保和再担保机构收益是变化的，因此本模型与现实有一定差距。进一步研究可聚焦于担保体系数据的进一步完善，对代偿率的随机过程进行定量描述，再利用具有随机收益的演化博弈形式，分析再担保体系的稳定演化条件，为再担保体系稳定发展提供更加贴近实际的理论参考。

[1] 吴建成，黄建. 再担保体系建设对中小微企业金融服务的影响问题研究[J]. 江苏社会科学，2014，(5)：91-96.

[2] 曾江候，侯赞. 中小企业再担保机构运作模式选择的数理分析[J]. 统计与决策，2007，(21)：137-140.

[3] 文学舟，梅强. 中小企业信用再担保体系建设及基本框架设计[J]. 企业经济，2008，(5)：169-171.

[4] 陈晓红，钟凡，韩文强. 我国再担保体系建立模式研究[J]. 理论前沿，2008，(8)：43-44.

[5] ADB (Asian Development Bank), Development of small and medium-sized enterprise credit guarantee companies [M/OL]. [2014-07-07]http://adb.org/sites/default/files/projdocs/2013/46023-001-prc-tar.pdf.

[6] Ju Yonghan, Sohn S Y. Stress test for a technology credit guarantee fund based on survival analysis [J]. Journal of the Operational Research Society, 2015, 66(3): 463-475.

[7] Chang W T, Yu C H, Kuo C J. A prediction of the probability of default of SMEs on the credit guarantee schemes [J]. Journal of Statistics & Management Systems, 2013, 16(2-3): 109-135.

[8] Kuo C J, Chen C M, Sumg C H. Evaluating guarantee fees for loans to small and medium-sized enterprises [J]. Small Business Economics, 2011, 37(2): 205-218.

[9] Oh I, Lee J D, Heshmati A. Evaluation of credit guarantee policy using propensity score matching [J]. Small Business Economics, 2009, 33(3): 335-351.

[10] 于孝建，徐维军.中小企业信用再担保各合作方的风险和收益分析[J]. 系统工程，2013，31(5)：33-39.

[11] 薛钰显，王东超. 中小企业信用再担保机构的风险分担比例研究[J]. 内蒙古社会科学(汉文版)，2013，(3)：103-106.

[12] 林平，袁中红.信用担保机构研究[J]. 金融研究，2005，(2)：133-144.

[13] 蔡文宇，陈玉菁. 我国中小企业信用担保引入政府补贴的可行性探讨：基于博弈论的视角[J]. 上海金融，2009，(12)：25-28.

[14] 财政部财政科学研究所课题组. 财政支持中小企业信用担保政策研究[J]. 经济研究参考，2010，(31)：2-34.

[15] 冯涛，徐肇成，郭蕾. 财政资助中小企业信用担保计划方式的比较研究[J]. 财政研究，2011，(8)：32-34.

[16] 马国建，张冬华. 中小企业信用再担保体系经济效益研究[J]. 软科学，2010，24(7)：111-115/120.

[17] 梅强，许红珍. 再担保体系内银保风险共担研究——基于系统动力学[J]. 技术经济与管理研究，2014，(2)：78-82.

[18] Dindo P, Tuinstra J. A class of evolutionary models for participation games with negative feedback [J]. Computational Economics, 2011, 37(3): 267-300.

[19] Antoci A, Borghesi S, Galeotti M. Environmental options and technological innovation: An evolutionary game model [J]. Journal of Evolutionary Economics, 2013, 23(2), 247-269.

[20] 曾江洪，崔晓云. 基于演化博弈模型的企业集团母子公司治理研究[J]. 中国管理科学，2015，23(2)：148-153.

[21] 李勇建，王治莹. 突发事件中舆情传播机制与演化博弈分析[J]. 中国管理科学，2014，22(11)：87-96.

[22] 郑君君，闫龙，张好雨，何鸿勇. 基于演化博弈和优化理论的环境污染群体性事件处置机制[J]. 中国管理科学，2015，23(8)：168-176.

[23] Webull J. Evolutionary game theory [M]. Princeton: Princeton Press, 1995.

[24] Friedman D. Evolutionary games in economics [J]. Econometric, 1991, 59(3): 637-666.

[25] 马知恩，周义仓. 常微分方程定性与稳定性方法[M]. 北京：科学出版社，2001.

Analysis on Evolutionary Stability Conditions for SMEs Credit Re-guarantee System

WANG Hui1,2, DENG Xiao-mei1, YANG Wei-hua2, FENG Ke1

(1. Department of Construction Management, Tsinghua University，Beijing 100084, China;2. Military Economics Academy, Wuhan 430035, China)

In countries with stable small and medium-sized enterprises (SMEs) credit re-guarantee system, SMEs credit guarantee companies are required to join the re-guarantee system, and every SMEs credit guarantee agreement is automatically guaranteed by re-guarantee company. However, SMEs credit re-guarantee system is not mandatory in China. An important question is what conditions shall be matched in order to form a stable SMEs credit re-guarantee system through market mechanism rather than compulsory means. To answer the question, an evolutionary game model between SMEs credit guarantee companies and re-guarantee companies was developed to explore the evolutionary stability conditions for SMEs credit re-guarantee system. The evolutionary stable strategies and corresponding conditions of the system were found by utilizing the stability theory of differential equations. Under the premise of steady development of the system, adjustable ranges of operating mechanisms in the re-guarantee system, such as risk sharing proportion, re-guarantee rate and minimum government subsidy, were also further discussed quantitatively. Lastly, a numerical example was provided to verify and applicate the conclusions. The results show that the stable development of SMEs credit re-guarantee system needs two conditions: the incremental payoff of re-guarantee companies has to be positive, and the incremental payoff of guarantee companies has to exceed the filing costs after SMEs credit guarantee companies joining in the SMEs credit re-guarantee system. The results also show that the compensation rate has significant influences on the operating mechanisms in the re-guarantee system. The greater the compensation rate, the lesser the adjustable range of risk sharing proportion and re-guarantee rate. Moderate government subsidy is needed if the adjustable range of risk sharing proportion and re-guarantee rate is absent. The research results provide theoretical references that can be used to improve China’s SMEs credit re-guarantee system.

SMEs credit re-guarantee system; evolutionary stability conditions; adjustable arranges

1003-207(2016)07-0001-10

10.16381/j.cnki.issn1003-207x.2016.07.001

2015-02-07；

2015-10-14

国家自然科学基金面上项目(71473145)

邓晓梅(1969-)，女(汉族)，四川人，清华大学建设管理系副教授，博士，研究方向：工程担保、工程管理，E-mail:dengxm@tsinghua.edu.cn.

F830

A