基于粒子群算法搜索的非侵入式电力负荷分解方法

李如意，黄明山，周东国，周 洪，胡文山



基于粒子群算法搜索的非侵入式电力负荷分解方法

李如意1，黄明山1，周东国2，周 洪2，胡文山2

(1.河南许继仪表有限公司，河南 许昌 461000；2.武汉大学动力与机械学院，湖北 武汉 430072)

非侵入式电力负荷分解是根据入口处电流、电压信号进行用电负荷辨识的一种方法。然而，由于电流、电压波动等因素干扰，单一特征所得到的分解结果通常会与实际用电设备投切结果不一致。为了可靠地提升在线非侵入式电力负荷分解能力，构建了基于谐波的电流特征表达并结合功率两个特征作为设备投切状态辨识的目标函数。同时，引入了正态分布的度量函数，将其融合并作为粒子群(Particle Swarm Optimization, PSO)算法的适应度函数，以此寻找最佳的电力负荷分解结果。最终，通过实验室开发的非侵入式负荷分解装置进行实验。实验结果表明所述方法能获得更好的在线电力负荷分解能力。

非侵入式；电力负荷分解；粒子群算法；适应度函数

0 引言

非侵入式电力负荷监测是一种仅通过安装在用户电力入口端的传感器获取电压、电流等信息便可获得家庭用电设备的投切情况的技术，从而帮助用户了解在不同时段各类用电设备的工作状态[1]。同时，也可以帮助用户制定合理的节能计划，并使用户有针对性地去开展节能手段[2]。对于电力企业而言，这种非侵入式电力负荷数据的获取，有助于预测电力系统的负荷组成[3-6]，实现国家电力资源的优化配置。因此，建设高效的负荷监测系统，成为了各个国家投入研究的重点。它不仅可为电力行业节能减排提供有力支撑[7]，同时在建设节约型社会和缓解能源压力等方面都具有十分重要的意义。

非侵入式负荷监测方法最早由Hart在20世纪80年代提出[8]，其主要监测电力入口处稳态功率的变化来实现负荷分解(其负荷分解流程如图1所示)，从而奠定了非侵入式电力负荷分解的基本框架。

图1非侵入式负荷分解基本框架

在图1所示框架中，集合分析是整个非侵入式电力负荷分解的基础。通常需要提取每个用电设备的可靠负荷印记(Label Signature, LS)，用以标识用电设备，以便后续进行分解与辨识。在现有的研究中，常用的负荷印记包括稳态谐波、功率特征、瞬态特征等[9-10]。文献[11-12]采用有功功率作为单一特征对用电设备进行识别；文献[13]采用稳态谐波信息，并通过智能优化算法进行最优电力负荷分解。相比于稳态特征，瞬态特征注重于描述用电设备投入运行的负荷细节，特别是用电设备开启瞬间的信息，它几乎可以作为用电设备唯一的标签[10, 14]。为此，一些研究者开始着眼于信息信号处理方法，例如小波分析[15]等。但是，瞬态特征劣势也相当明显，例如需要高采样率及持续的处于监测状态。而且瞬态特征不具有叠加性，当多个设备一同工作或投切时的干扰，都会直接影响电力负荷的准确分解与辨识。在最近的一些研究中，低采样非侵入式电力负荷分解成为了共同关注的目标[11, 16-17]。

为了有效辨识用电设备投切状态，一般而言，除了与用电设备标签特征相关之外，还与后续的优化或辨识算法有关。文献[16]采用多状态隐马尔科夫模型并采用新的Viterbi算法进行电力负荷分解；文献[17]提出了一种采用减除聚类和最大似然分类器，对开关类用电设备进行负荷分解；文献[18]采用贝叶斯方法来实现对用电设备有功功率进行状态估计；文献[19]采用SVM/GMM的混合模型完成负荷分解的任务。相比于那些采用模式识别算法负荷分解，构建新的最优化目标函数不失为一种好的电力负荷分解方式。文献[20]采用整数规划的方法来对家庭电力设备进行分解；文献[21]将电力负荷分解转化为背包问题，并采用优化算法进行分解；而文献[13]则采用微分进化算法对谐波及相角信息进行分解，以辨识用电识别的投切。一般而言，构建不同的最优化目标函数可能会求解得到不一样的负荷分解结果。事实上，一个好的最优化目标函数是决定最终取得最优电力负荷分解结果的关键。为此，本文结合用电设备稳态工作下电流特征、功率等信息构建了最优化目标函数，并作为粒子群算法的适应度函数进行最优搜索。最后在实验室所开发的平台上实验，验证了本文电力负荷分解方法的有效性。

1  非侵入式电力负荷稳态特征及功率

通常，用电设备正常工作稳态电流存在一定的统计规律特性[9]，而且根据基尔霍夫电流定律，一个入口节点的电流由各个出口支路的电流线性叠加得到，即总电流是各个用电设备投切时电流的叠加。为了构建电流特征表达模型，本文引入信号的频域表达理论，将电流信号用一组谐波进行表征，以此作为用电设备特征。

为了便于分析，这里假定一个用户家庭有个设备可进行投切，则可以建立如式(1)方程组。

式中，I为电流I分解到次谐波上的幅值。一般而言，在电流信号中，以{(),()} ，=1,2,…,作为基函数具有很好的表达效果。为此，将对每个cos(kωt+θ)用如式(2)方式进行表达。

式中：为基波角频率；表示谐波次数；s和t分别表示系数。例如某一个用电设备工作时，一个周期内的电流如图2(a)所示，通过分解，最终可以得到的结果如图2(b)所示。

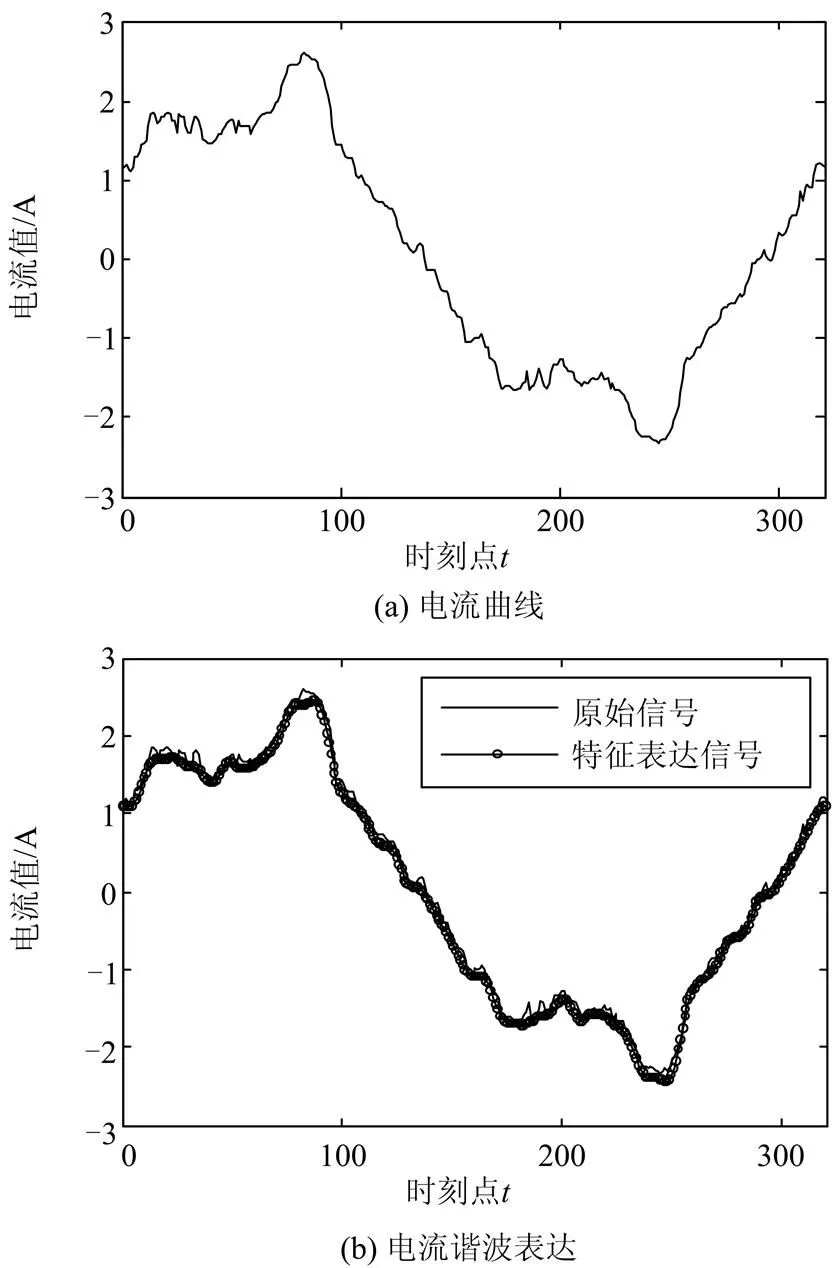
图2谐波电流特征表达及其逼近效果

进一步地，从式(2)可得到相位角θ为

同时，可计算用电设备的功率为

特别注意的是，式(2)中由于A/D采样频率的约束，通常只取前个谐波分量，从而得到了用电设备特征标签的个谐波进行表达。

考虑到大多数常用用电设备状态都可以用投入和关闭表示，为了方便，令a表示设备的投切状态(a=1表示投入，a=0表示关闭)。于是，负荷分解就可以转换为如式(5)目标函数。

式中：m表示入口处的总电流m中第个谐波系数；||.||表示2范数。因此，非侵入式电力负荷分解其本质上就是求解一组最优的1,…,a。

此外，每个设备的功率信息也具有一定的叠加性，即认为总功率是每个设备投切状态时功率的累加和。因此可构建如式(6)优化目标函数对电力负荷功耗进行分解。

式中：P是数据库第个设备的功率；为当前功率。

由于式(5)和式(6)属于整数最优化规划，为了寻找最优解，本文将上述两种特征进行融合作为最优化目标函数，并嵌入到粒子群(Particle Swarm Optimization, PSO)算法的适应度函数中，通过PSO算法的求解找到最优的1,…,a，使得式(5)和式(6)同时达到最优，即实现非侵入式电力负荷在线分解。

2  粒子群最优电力负荷分解方法

2.1 粒子群算法简介

粒子群算法是一种由Eberhart和Kennedy根据鸟群捕食的行为所开发的进化计算方法。通常，在将其应用于优化问题求解过程中，认为每个可行解作为一个“粒子”，所有的粒子都有一个被适应度函数所决定的适应值。同时，每个粒子还有一个速度决定它们飞翔的方向和距离。然后，这些粒子追随当前的最优粒子值和个体极值在解空间中进行迭代更新，最终收敛于最优解，其整个算法流程如图3所示。

在粒子群算法中，粒子的更新以及速度按照如下方式进行。

式中：为粒子的维数；为惯性权重，用于平衡“开发”与“探测”能力；1和2为学习因子，通常取[0, 2]之间的正常数；1和2是介于[0, 1]之间的随机值；为约束因子，用于控制速度的权重。另外，位置变化和速度变化需根据实际情况进行相应约束，使其不超过边界值。

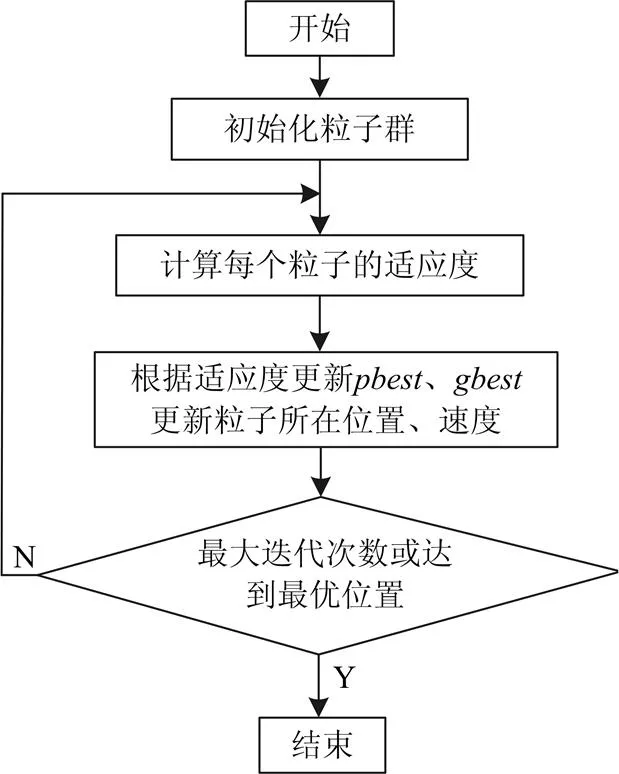
图3粒子群算法流程图

2.2 适应度函数构建

在PSO算法以及诸如遗传算法等进化算法中，适应度函数是度量群体中各个个体有可能达到或有助于找到最优解的优良程度。在实际应用中，适应度函数通常由最优化目标函数所替代，例如在本文中，适应度函数可由式(5)和/或式(6)所构建。一般而言，不同的适应度函数可能会求解得到不一样的电力负荷分解结果。事实上，一个优良的适应度函数是决定最终取得最优电力负荷分解结果的关键。

由于用电设备的电流谐波特征或者功率特征，在一定程度上容易受到用电线上电压、电流波动等干扰，特别是小功率和大功率设备一起投入时，单一特征所构建的目标函数对最终负荷分解结果的准确性会产生一定影响。因此，为了获得准确的电力负荷分解结果，本文将式(5)和式(6)合在一起，构建PSO算法的适应度函数，基于此搜寻最佳的1,…,a，即同时实现式(5)和式(6)最优。基于此，本文首先引入以正态分布形式的一个度量函数，其表达式如式(9)所示。

式中，参数σ标准差，用来调整分布。显然，其f(d)值由d和σ共同决定。然后，将其以乘积的方式进行结合，得到PSO的适应度函数：

式(10)中，1和2根据样本数据库进行人工设置。在本文中，设置1=1，2=100。

从式(10)可以看出，适应度函数值是由1和2的值共同决定。特别地，当1达到最小而2有较大偏差，或者2达到最小而1有较大偏差时，式(10)在一定程度上会弥补因单个目标函数(式(5)或式(6))所决定的负荷分解错误，从而为提高电力负荷分解结果的准确性奠定基础。

进一步地，为了便于说明整个PSO算法搜索过程，其主要步骤如下：

1) 设置初始化种群大小，维数，学习因子1和2，惯性权重，约束因子=1；

2) 在解空间范围内[0, 2-1]，随机设置粒子群初始位置值x(每个粒子的位置值均由二进制值(12…a)所对应的十进制表示)，初始速度值v；

3) 根据粒子群位置值，计算适应度函数式(10)，记录每个个体适应度极值所对应的位置，以及适应度函数全局最大值所在位置；

4) 根据以及，由式(7)和式(8)更新速度x和位置v；

5) 如果迭代次数未超过预设值以及当前的最优适应度值非最优，则转到步骤3)；否则，停止迭代，输出最优个体位置值，即最优解。

3 算例分析

本方法在研究室所开发的非侵入式负荷分解硬件平台上实验，如图4所示，并采用8种常用的用电设备(微波炉，电风扇，台式电脑，烧水壶，电热器，取暖器，电饭煲，电视机，分别用1,…,8标记)进行测试，共256种组合。在数据库中，首先将采集得到的电流、电压进行存储，然后提取15次谐波和其平均功率作为特征，其平均功率如表1所示，电流及其谐波幅值如图5所示，其中各次谐波所对应的幅值详见表2。

图4非侵入式负荷装置样机

表1实验所使用的用电设备功率信息

Table 1 Power information of devices

表2家用设备正常工作下电流的15次谐波幅值

Table 2 Harmonic value of device in home

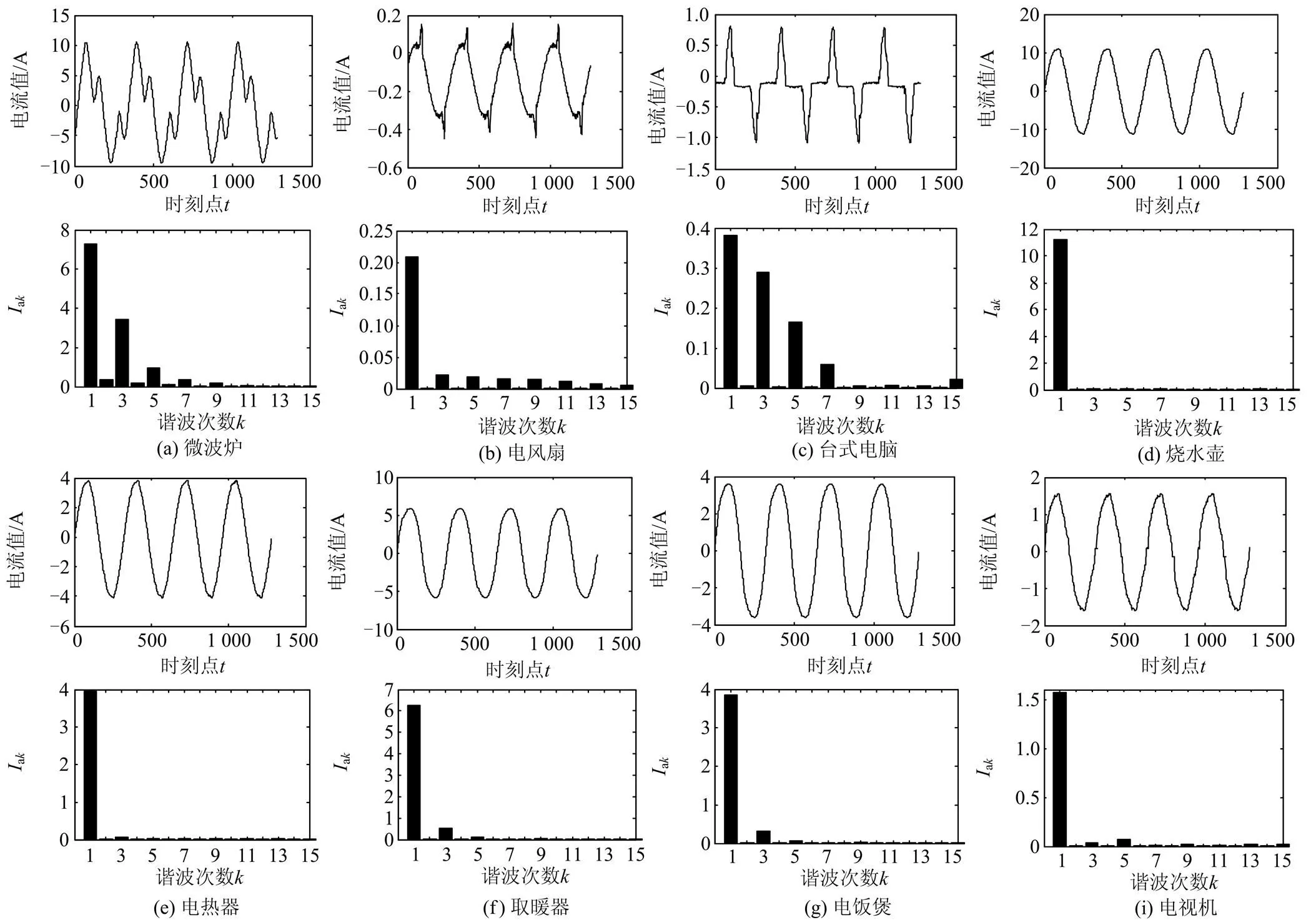
图5用电设备电流及k次谐波幅值

实验中，设置PSO算法每一个粒子位置值由二进制值(12345678)所对应的十进制表示，种群数为10个，惯性因子设置为0.8，学习因子均为0.5，最大迭代次数为50，约束因子为1。

为了说明本文所构建的适应度函数的有效性，在实验中，分别采用式(5)和式(6)作为适应度函数进行对比，得到的实验结果如表3所示。从表中可以看出，本文所构建的目标函数在一定程度上要优于式(5)或式(6)所对应的目标函数。

表3电力负荷分解测试结果

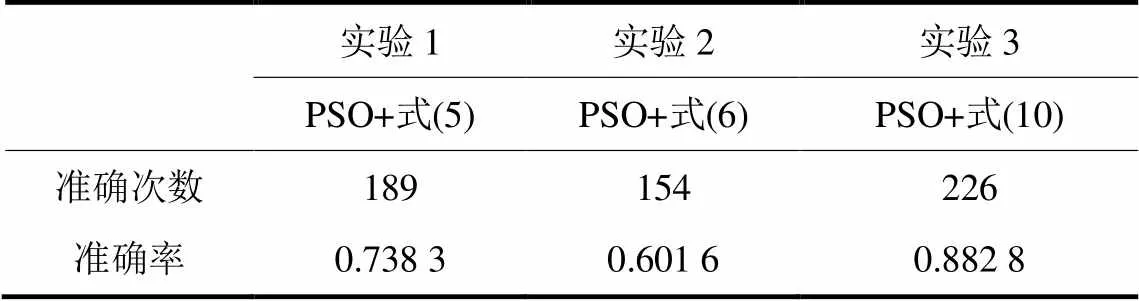
Table 3 Results of non-intrusive load disaggregation

此外，为了直观描述本文方法在线非侵入式电力负荷分解性能，表4给出了采用式(5)和/或式(6)发生分解错误而式(10)方法分解正确的典型的三个案例，即分别是三种设备、四种设备、五种设备共同工作，其他设备处于关闭状态，其中电流及其谐波表达如图6所示。最终，对应的实测结果如表5所示。从表中可以看出，式(6)所构建的目标函数主要考虑功率特征，因此当多个设备投切时，容易发生误分解，例如测试实例2，实测功率为2 097.1 W。从数据库上看，电风扇、台式电脑、烧水壶以及电视机组合功率为2 092.5 W，而微波炉和取暖器的功率和为2 101 W。显然后者比前者更接近实测功率，因此发生分解错误。相比而言，采用式(5)作为目标函数，其负荷分解率要高于采用式(6)，其主要归结于谐波特征具有更加丰富的信息。但总的而言，本文方法结合谐波特征和功率特征，更适合于非侵入式电力负荷分解。

另外，图7给出了PSO方法关于第一个测试例子的收敛性。从图中可以看出，PSO在迭代18次后进入稳定，得到的粒子的位置为100，转化为二进制值01100100后，可得电风扇、台式电脑以及取暖器在工作，与实际情况设备状态开启一致。

表4电力负荷分解测试例子

Table 4 Examples of non-intrusive load disaggregation

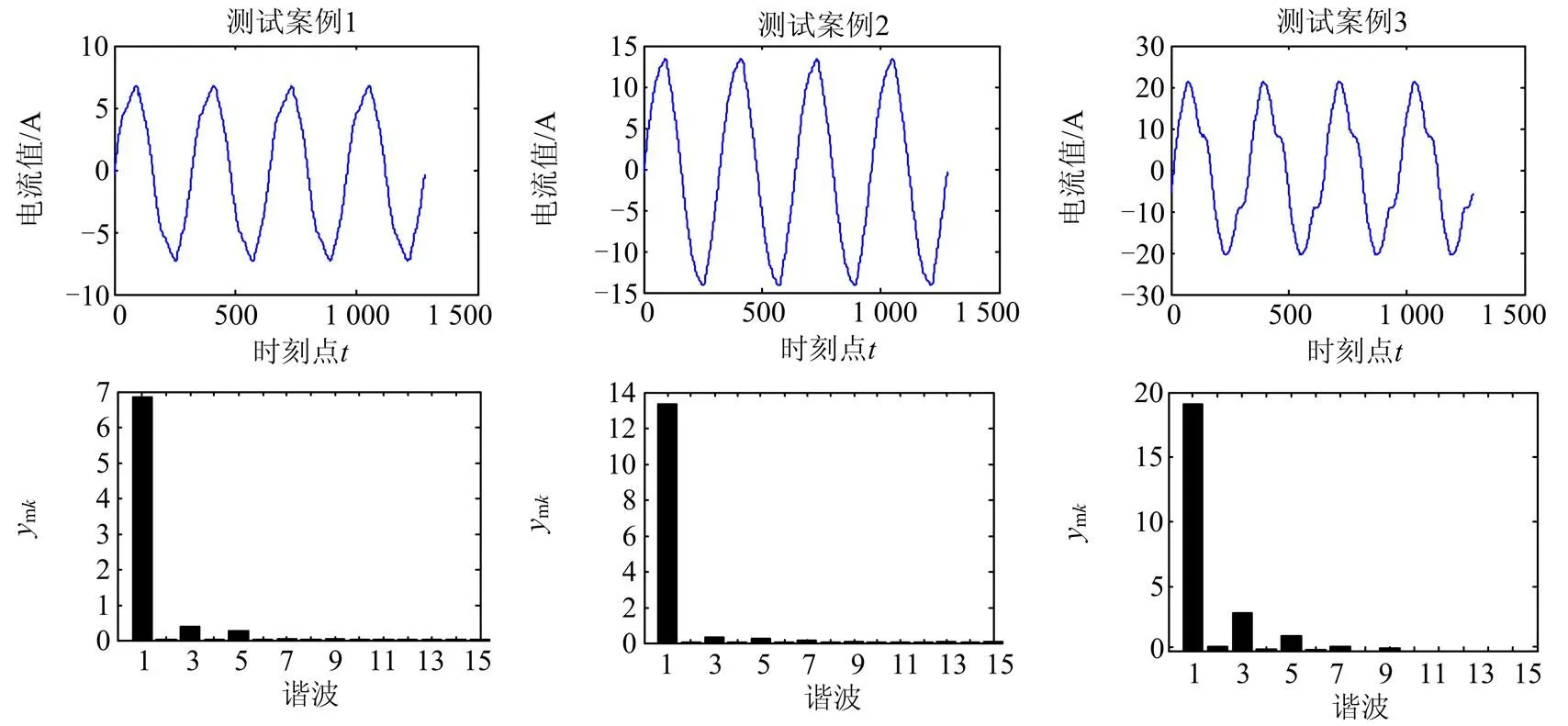
图6测试案例电流及其k次谐波幅值

表5电力负荷分解测试例子结果

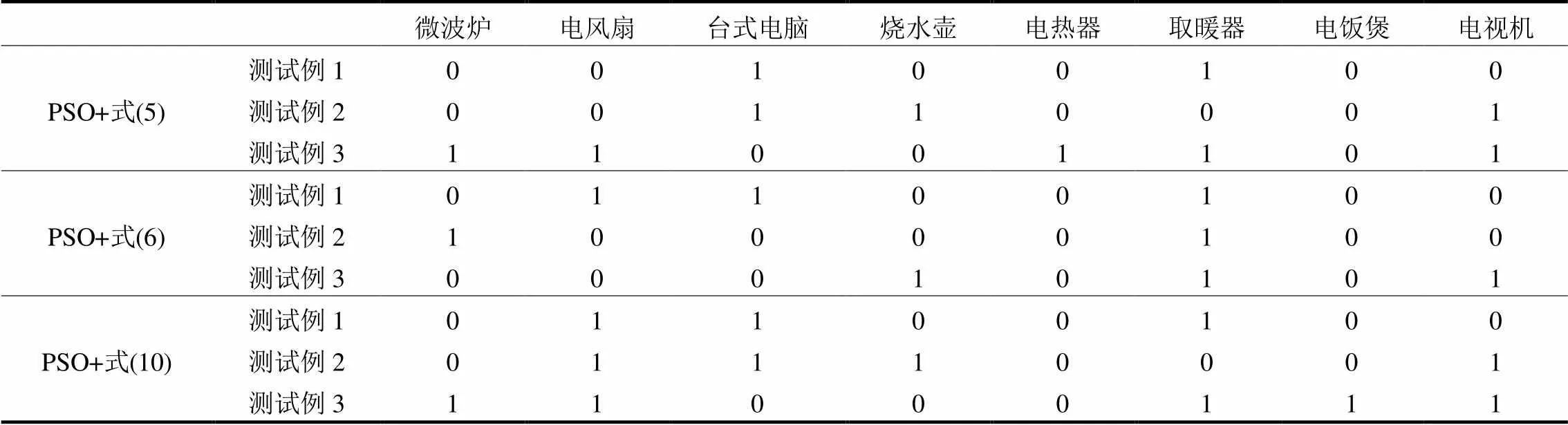
Table 5 Results of examples of non-intrusive load disaggregation

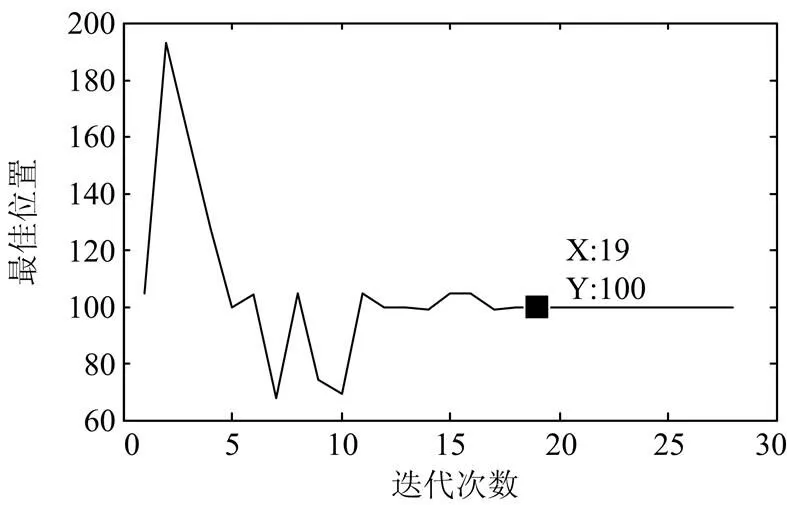
图7 PSO算法的收敛性

4 结语

为了提高电力负荷分解性能，本文提出了一种以电流的谐波表达作为特征，并结合功率特征对用电设备进行表征，构建了一种正态分布形式的度量函数，并以此作为粒子群最优搜索算法的适应度函数，实现非侵入式电力负荷分解。实验及案例比较分析，结果验证了本文方法较单一特征作为PSO适应度函数进行电力负荷分解更优，且其准确率超过80%，具备了较好的在线非侵入式电力负荷分解能力。在下一步中，我们将会深入展开多状态设备的状态辨识方法，更进一步提高用户用电体验。

[1] 鲍伟, 高翔, 沈冰, 等. 智能变电站非侵入式测试技术研究[J]. 电力系统保护与控制, 2015, 43(20): 125-129.

BAO Wei, GAO Xiang, SHEN Bing, et al. Research method of "non-intruding test" for smart substation[J]. Power System Protection and Control, 2015, 43(20): 125-129.

[2] 郑小霞, 刘庆强, 林顺富, 等. 面向非干预式负荷监测的居民负荷微观特性研究[J]. 电力系统保护与控制, 2014, 42(10): 62-70.

ZHENG Xiaoxia, LIU Qingqiang, LIN Shunfu, et al. Research of the microscopic signatures of residential loads for NILM[J]. Power System Protection and Control, 2014, 42(10): 62-70.

[3] 马哲, 舒勤. 基于ESPRIT分解算法的短期电力负荷预测[J]. 电力系统保护与控制, 2015, 43(7): 90-96.

MA Zhe, SHU Qin. Short term load forecasting based on ESPRIT integrated algorithm[J]. Power System Protection and Control, 2015, 43(7): 90-96.

[4] 李龙, 魏靖, 黎灿兵, 等. 基于人工神经网络的负荷模型预测[J]. 电工技术学报, 2015, 30(8): 225-230.

LI Long, WEI Jing, LI Canbing, et al. Prediction of load model based on artificial neural network[J]. Transactions of China Electrotechnical Society, 2015, 30(8): 225-230.

[5] 谷云东, 张素杰, 冯君淑. 大用户电力负荷的多模型模糊综合预测[J]. 电工技术学报, 2015, 30(23): 110-115.

GU Yundong, ZHANG Sujie, FENG Junshu. Multi-model fuzzy synthetic forecasting of electric power loads for larger consumers[J]. Transactions of China Electrotechnical Society, 2015, 30(23): 110-115.

[6] 马斌, 张丽艳. 一种基于径向基神经网络的短期风电功率直接预测方法[J]. 电力系统保护与控制, 2015, 43(19): 78-82.

MA Bin, ZHANG Liyan. Short-term wind power direct forecasting based on RBF neural network[J]. Power System Protection and Control, 2015, 43(19): 78-82.

[7] 刘文学, 梁军, 贠志皓, 等. 考虑节能减排的多目标模糊机会约束动态经济调度[J]. 电工技术学报, 2016, 31(1): 62-70.

LIU Wenxue, LIANG Jun, YUN Zhihao, et al. Multi- objective fuzzy chance constrained dynamic economic dispatch considering energy saving and emission reduction[J]. Transactions of China Electrotechnical Society, 2016, 31(1): 62-70.

[8] HART G W. Nonintrusive appliance load monitoring[J]. Proceedings of the IEEE, 1992, 80(12): 1870-1891.

[9] AHMED Z, ALEXANDER G, MUHAMMAD A I, et al. Nonintrusive load monitoring approaches for disaggregated energy sensing: a survey[J]. Sensors, 2012, 12: 16838- 16866.

[10] LIANG J, NG S K K, KENDALL G, et al. Load signature study — part I: basic concept, structure, and methodology[J]. IEEE Transactions on Power Delivery, 2010, 25(2): 551-560.

[11] DINESH C, NETTASINGHE B W, GODALIYADDA R I, et al. Residential appliance identification based on spectral information of low frequency smart meter measurements[J]. IEEE Transactions on Smart Grid, 2015: 1-12.

[12] PARK H. Load profile disaggregation method for home appliances using active power consumption[J]. Journal of Electrical Engineering and Technology, 2013, 8(3): 572-580.

[13] 黎鹏, 余贻鑫. 非侵入式电力负荷在线分解[J]. 天津大学学报, 2009, 42(4): 303-308.

LI Peng, YU Yixin. Non-intrusive method for online power load decomposition[J]. Journal of Tianjin University, 2009, 42(4): 303-308.

[14] HASSAN T, JAVED F, ARSHAD N. An empirical investigation of V-I trajectory based load signatures for non-intrusive load monitoring[J]. IEEE Transactions on Smart Grid, 2014, 5(2): 870-878.

[15] CHANG H H, YANG H T, LIN C L. Load identification in neural networks for a non-intrusive monitoring of industrial electrical loads[J]. Lecture Notes in Computer Science, 2008, 5236: 664-674.

[16] MAKONIN S, POPOWICH F, BAJIC I V, et al. Exploiting HMM sparsity to perform online real-time nonintrusive load monitoring[J]. IEEE Transactions on Smart Grid, 2015: 1-11.

[17] HENAO N, AGBOSSOU K, KELOUWANI S. Approach in nonintrusive type I load monitoring using subtractive clustering[J]. IEEE Transactions on Smart Grid, 2015.

[18] MARCHIORI A, HAKKARINEN D, HAN Q, et al. Circuit-level load monitoring for household energy management[J]. IEEE Pervas Comput, 2011, 10(1): 40-48.

[19] LAI Y X, LAI C F, HUANG Y M, et al. Multi-appliance recognition system with hybrid SVM/GMM classifier in ubiquitous smart home[J]. Information Science, 2013, 230: 39-55．

[20] SUZUKI K, INAGAKI S, SUZUKI T, et al. Non-intrusive appliance load monitoring based on integer programming[C] // Proceedings of SICE Annual Conference, USA, 2008: 2742-2747.

[21] LIN Y H, TSAI M S. Development of an improved time-frequency analysis-based nonintrusive load monitor for load demand identification[J]. IEEE Transactions on Instrumentation and Measurement, 2014, 64(6): 1470-1483.

(编辑 魏小丽)

Optimized nonintrusive load disaggregation method using particle swarm optimization algorithm

LI Ruyi1, HUANG Mingshan1, ZHOU Dongguo2, ZHOU Hong2, HUWenshan2

(1. Henan Xuji Instrument Co., Ltd., Xuchang 461000, China; 2. School of Power and Mechanical Engineering, Wuhan University, Wuhan 430072, China)

Nonintrusive load disaggregation is a kind of method for recognizing the state of appliances by using the current and voltage in the power bus. However, the obtained results are usually not coincided with the actual results, because of the fluctuation of current and voltage. To promote the performance of disaggregation, the effective features are built by the harmonic of current and the feature of real power. And particularly, the measurement function which is utilized to combine the harmonic of current and the feature of real power together is introduced into the fitness function inherent in the particle swarm optimization (PSO) algorithm, thus finding the optimal results of energy disaggregation using PSO algorithm. Finally, experiments are performed on the hardware equipment developed by our Labs. The results demonstrate the good performance for energy disaggregation online.

non-intrusive; load disaggregation; particle swarm algorithm; fitness function

10.7667/PSPC160239

2015-11-28；

2016-03-07

李如意(1965-)，男，硕士，高工，研究方向为机电控制及自动化；

黄明山(1962-)，男，硕士，高工，从事电气工程方向研究；

周东国(1985-)，男，通信作者，博士，讲师，研究方向为智能电网、模式识别。E-mail: dgzhou1985@whu.edu.cn