基于元件层级和电源可达性的配电网可靠性评估混合算法

胡美玉，胡志坚，邓奥攀，王小飞，汪 祥



基于元件层级和电源可达性的配电网可靠性评估混合算法

胡美玉，胡志坚，邓奥攀，王小飞，汪 祥

(武汉大学电气工程学院，湖北 武汉 430072)

提出一种配电网可靠性快速评估算法以解决重复遍历网络拓扑的问题。以开关元件为界形成配电系统元件分区和负荷分区。提出建立元件等级和开关层级以直接判断动作保护元件的位置，结合高度稀疏的等效支路连接矩阵快速分析负荷与电源及备用电源之间的可达性，建立等效负荷故障后果模式列表。采用序贯蒙特卡罗模拟，根据元件所属分区搜索负荷故障类型，统计故障停电次数和停电时间，计算可靠性指标。分别以各元件分摊的负荷故障时间和系统缺供电能量辨识负荷点和系统的薄弱环节。算例验证结果表明，该算法能正确高效地计算可靠性指标，适用于复杂配电网可靠性评估。

可靠性评估；元件等级；开关层级；可达性；薄弱环节

0 引言

配电系统作为连接发输电系统与用户的纽带，反映了电力系统对用户连续供电的能力，其可靠性集中体现了整个电力系统的结构及运行特性[1]。统计表明[2]，在所有用户停电故障中，80%以上是由电力系统的配电环节故障导致的。随着用户对供电可靠性要求的提高，可靠性评估以及薄弱环节的辨识对配电网改造和规划具有重要的意义。

配电系统采用的可靠性评估方法主要有状态枚举法和蒙特卡罗模拟法(Monte Carlo simulation，MCS)[3-8]。其中状态枚举法主要包括故障模式后果分析法[9](Failure mode and effect analysis，FMEA)和状态空间法[10]。采用故障模式后果分析法，需要依次枚举配电系统所有可能的元件故障，随着配电系统规模的增大，故障模式后果分析表非常庞大。在FMEA的基础上，网络等值法[11]将网络结构转化成简单辐射状配电网的可靠性评估，但是不能一次性形成负荷和系统的可靠性指标。最小路法[12]、最小割集法[13-14]将待枚举的故障元件限制在最小路和最小割集中，但是建立复杂系统的最小路和最小割集需花费大量的时间。文献[15]结合递归算法和网络等值法，利用树的递归遍历实现配电网的等值过程；级别树算法[16]通过形成开关树和断路树，简化系统结构和故障遍历过程；逆流传递和顺流归并法[17]通过逆流传递计算下游故障的影响和顺流归并计算上游故障的影响；文献[18]采用贝叶斯网络法在评估配电系统可靠性的同时辨识系统薄弱环节。

配电网可靠性评估的实质是判断负荷点与电源点之间是否有连接通路的问题，文献[19]将可达性分析引入配电网可靠性评估中，用于判断故障后果模式，能有效避免对网络拓扑进行搜索。但是存在以下几点问题：1) 对配电网中所有节点建立邻接矩阵，邻接矩阵的规模庞大；2) 需要在故障模拟前形成故障大、小区域，而不能直接判断动作开关的位置；3) 隔离小区域故障时，直接断开邻接矩阵中故障区域的所有邻接关系，这并不适用于分析开关故障时负荷类型。4) 不能模拟系统的演变过程和辨识薄弱环节。

本文提出了一种面向动作开关和电源可达性通路的贝叶斯网络时序模拟法用于配电系统可靠性评估。该算法首先形成配电系统元件分区和负荷分区，根据元件等级、开关层级快速确定各阶段动作保护元件的位置，动态修改等效支路连接矩阵，通过电源可达性通路分析建立元件块-负荷块故障后果列表，可有效避免重复遍历网络拓扑；然后采用MCS模拟元件故障事件，直接搜索状态列表确定负荷块故障类型，引入熔断器因子简化元件与电源之间有无熔断器影响，提高了配电系统可靠性指标的计算速度；运用贝叶斯网络诊断推理算法，辨识配电系统薄弱环节。结合实例计算，验证了该算法的高效性和正确性。

1  可达性分析

1.1 建立配电系统分区

实际配电系统的开关元件数量相对较少，并且能在系统故障时迅速隔离故障。针对配电系统这一特点，本文以图1所示的简单辐射状配电网为例，暂时不考虑负荷支路上熔断器的影响，以断路器或隔离开关为边界建立分区。图中B1~B2表示断路器，L1~L12表示馈线，T1~T5表示变压器，F1~F5表示熔断器，LP1~LP5表示负荷，N/O表示联络开关，S表示隔离开关。

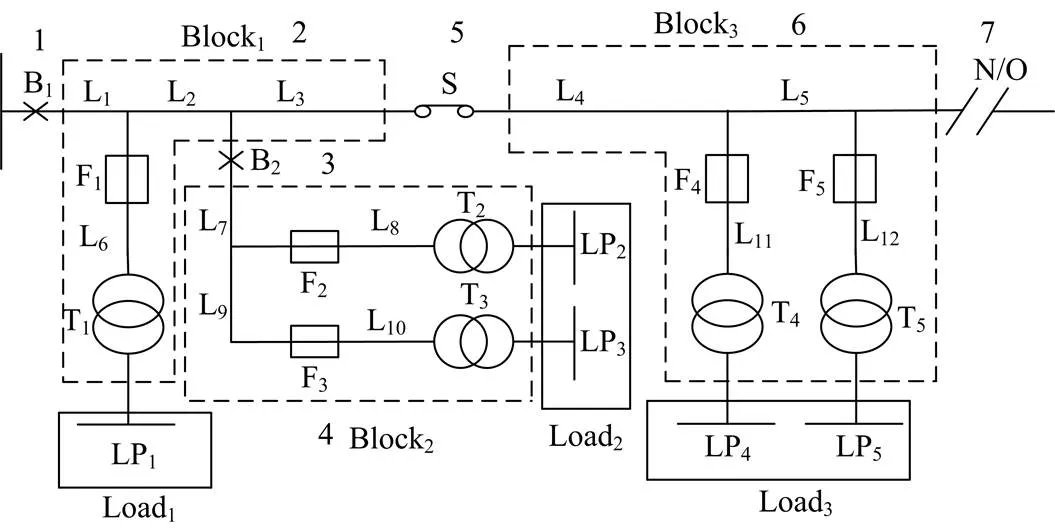
图1简单辐射状配电网

配电系统元件分区的原则是分区中任意元件故障导致的故障后果模式相同；负荷分区的原则是任意元件块故障导致的负荷故障类型均一致。同一分区的元件统一处理，同一分区的负荷故障类型统一存储，可以减小网络规模和存储空间，提高可靠性评估速度。

1.2 等效配电系统支路连接矩阵

图1所示的原配电系统总支路数为26，节点数为27，原始配电系统节点邻接矩阵是一个方阵，而等效后系统的支路连接矩阵是一个的方阵。矩阵是一个高度稀疏的对称矩阵，且对角元素全为0，计算时只需对上三角元素进行动态修正。

可达性是指节点或者支路之间的连通关系，通过配电系统支路连接矩阵可得支路的可达性矩阵：

为方便分析故障负荷类型，假设系统中所有开关为闭合状态，则可达性矩阵，系统各支路都是连通的。

1.3 负荷的故障类型

由于开关能迅速隔离故障，不同位置负荷点的停电持续时间并不相同。根据故障停电时间长短，将负荷分为以下四类。

A类：不受故障影响；

B类：故障时间为隔离开关操作时间；

C类：故障时间为隔离开关操作时间与联络开关切换时间之和；

D类：故障时间为元件的故障修复时间。

配电系统发生故障后，负荷故障类型是由动作开关的位置和电源可达性通路决定的，判定过程包括以下四步：

1) 确定故障元件的位置；

2) 确定动作断路器的位置，隔离故障大区域；

3) 确定最小故障分区的隔离开关(断路器、隔离开关、联络开关)的位置，隔离故障小区域；

4) 判断负荷与电源及备用电源的可达性。

开关动作的原则是在隔离故障的同时尽可能靠近故障元件，减小停电范围。为了能够快速准确地确定步骤2)和步骤3)中动作开关的位置，本文提出元件分级和开关分层的概念。

定义1：元件等级

同一等级馈线上元件等级相同，并且根据同一等级馈线数目同相连上一级馈线首端(靠近主电源侧)距离的远近对馈线进行编号。主馈线等级为1且只有一条，编号为1。定义主馈线的分支馈线为二级馈线，二级馈线的分支馈线为三级馈线，依此类推。二级馈线等级为2，根据二级馈线与主馈线首端的距离由近及远，依次编号为1, 2,…；三级馈线等级为3，根据三级馈线与二级馈线首端的距离以及二级馈线的编号由近及远进行编号，如二级馈线的编号为1，三级馈线依次编号为11, 12,…。图1所示的配电网中，等级为1的开关有B1、S、N/O；等级为2的开关有B2。

定义2：开关层级

设主馈线首端断路器层级为1，根据分区后开关与主电源距离的由近及远，依次为2, 3,…。

开关分级分层矩阵建立如下：

认为配电系统中断路器、隔离开关、联络开关均能100%可靠动作。结合各馈线出线处均设置断路器的特点，根据故障元件的类型和位置，可分为以下三种情况判定负荷故障类型。

情况1：故障元件不是母线或者各馈线首端断路器。

3) 分析可达性矩阵，若支路与主电源连接值为1，则该支路上的负荷为A类；否则为待处理支路。

6) 分析可达性矩阵，若待处理支路与主电源连接值为1，则该支路上的负荷为B类；若待处理支路与备用电源连接值为1，则该支路上的负荷为C类；若待处理支路与所有电源连接值为0，则该支路上的负荷为D类。

以图1中支路6故障为例说明上述过程，第一步，支路6等级为1，矩阵中等级为1并且最靠近支路6的断路器为支路1，此时支路连接矩阵以及可达性矩阵为

由式(6)中主电源直接相连支路1所在行可知，此时所有负荷支路与主电源之间均没有通路，所有负荷支路均为待处理支路。

第三步，支路5开关层级为2，故障支路之后等级为1与开关层级差值最小的为支路7，直接在原始连接矩阵中断开支路5和支路7。此时可达性矩阵如式(7)所示。

由式(7)可知，Load1、Load2与主电源之间有通路，为B类负荷；Load3与备用电源和主电源都没有通路，为D类负荷。

情况2：母线及主馈线首端断路器故障。

1) 搜索故障元件之后等级为1的断路器，搜索到的第一个断路器以及该断路器之前的二级馈线断路器(不包括故障元件)为动作断路器。

2) 搜索动作断路器之前是否有隔离开关，若有则断路器支路闭合，隔离开关支路断开；否则断路器支路断开。

母线或主馈线首端断路器故障，负荷只能为C类或D类，因此只需判断负荷与备用电源是否有通路。

情况3：分支馈线首端断路器故障。

步骤2)、步骤3)和步骤4)中搜索到的开关均为隔离小区域故障的开关，故障类型的判断过程与情况1相同。并且情况3也适用于子馈线首端断路器拒动的情况。

2  基于MCS的贝叶斯推理算法

序贯MCS是根据元件的故障时间与修复时间的概率分布以及随机数发生器，对元件状态进行抽样，得到系统组合状态。

2.1 元件模型

配电系统的元件主要包括传输线路、变压器、断路器、隔离开关、联络开关、熔断器。从可靠性的角度来看，配电网内的元件都是可修复元件，因此，配电网可以看作是一个可修复的系统[20]。

开关元件不可靠动作可以用概率来表示，因此配电系统元件均可用两状态模型表示。“1”表示正常工作状态，持续时间为元件平均无故障工作时间(Time to Failure, TTF)，“0”表示故障状态，持续时间为元件平均故障修复时间(Time to Repair, TTR)。本文采用指数分布作为元件无故障工作时间和故障修复时间服从的概率分布。

2.2 模拟法评估流程

步骤2：建立配电系统分区(元件分区、负荷分区)，生成负荷故障类型列表。

步骤3：生成与故障率不为0元件数对应的随机数，根据式对各元件状态持续时间进行采样，，则为故障元件，并将该最小工作时间累加至系统仿真时间。

步骤6：计算可靠性指标和停电时间概率分布。

2.3 贝叶斯诊断推理的实现过程

贝叶斯诊断推理为：在结果已发生的前提下，计算引起结果发生的某种原因发生的概率。结合负荷故障类型分类，负荷点故障的概率可表示为

经理论推导可知，负荷故障后验概率的大小取决于元件的可靠性参数，故障率与修复时间乘积最大的元件为负荷点的薄弱环节[18]。本文采用影响负荷的各元件故障时间与负荷总故障时间的比值表示后验概率，以后验概率最大者为负荷点的薄弱环节。

2.4 可靠性指标计算公式

配电系统主要可靠性指标均可由负荷点可靠性指标计算得到。负荷点可靠性指标计算如下：

负荷停运率的概率分布可用式(14)计算。

3  算例分析

本文采用IEEE RTBS Bus6中的馈线F4~F7组成的子系统为算例，如图2所示。该系统包括23个负荷，23个熔断器，23台配变，30条线路，4台断路器和1个分段开关。该系统参数引自文献[22-23]。

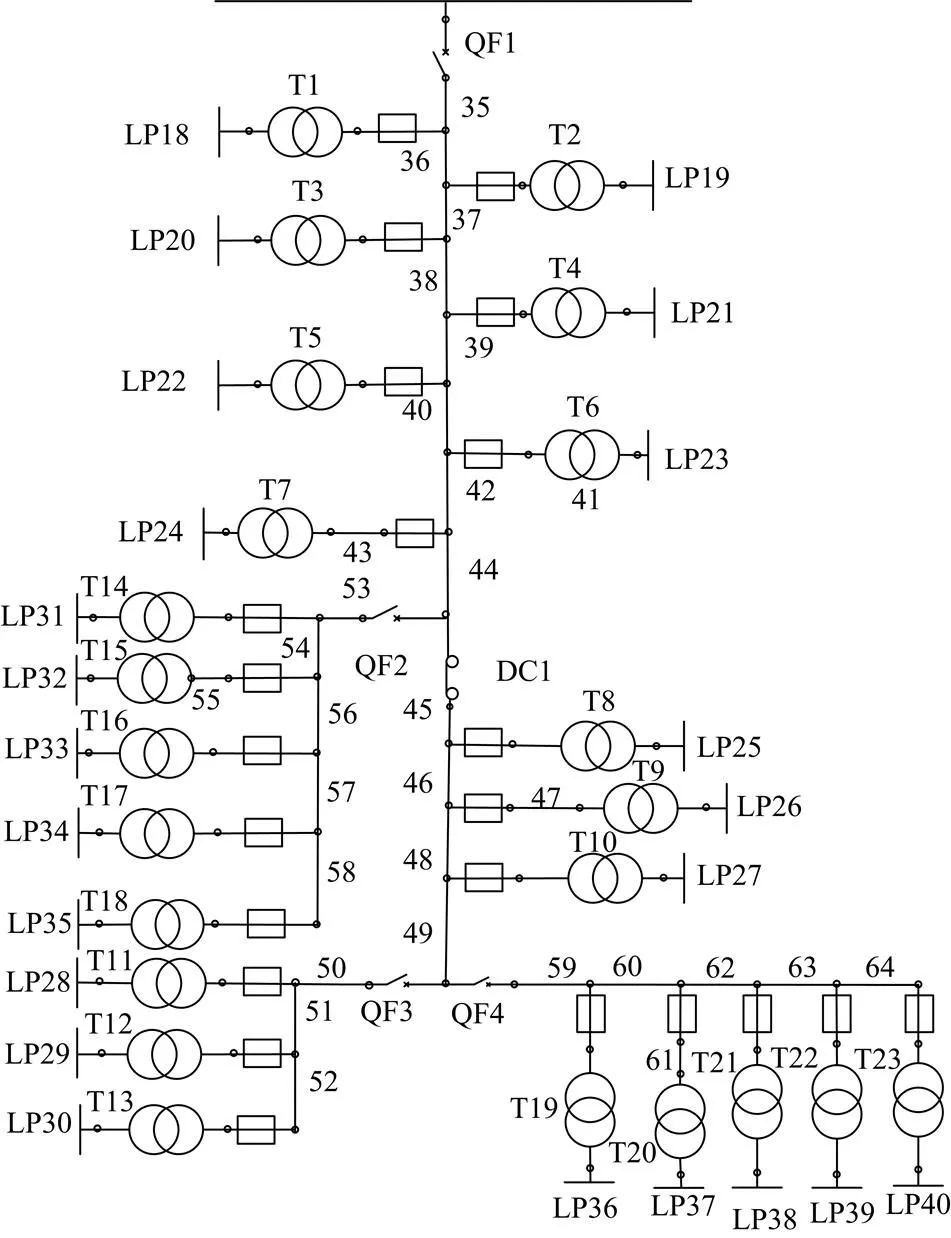
图2 IEEE RTBS Bus6子系统接线图

在Matlab R2013a中分别应用遍历算法，结合可达性分析结果的解析法和模拟法对算例进行可靠性评估。设断路器可靠熔断的概率为f=100%，分段开关、联络开关的切换时间均为1 h，变压器无备用。多次模拟结果表明可靠性评估结果是收敛的，不考虑开关及母线故障时，部分负荷的可靠性计算结果如表1所示。

表1部分负荷点可靠性指标

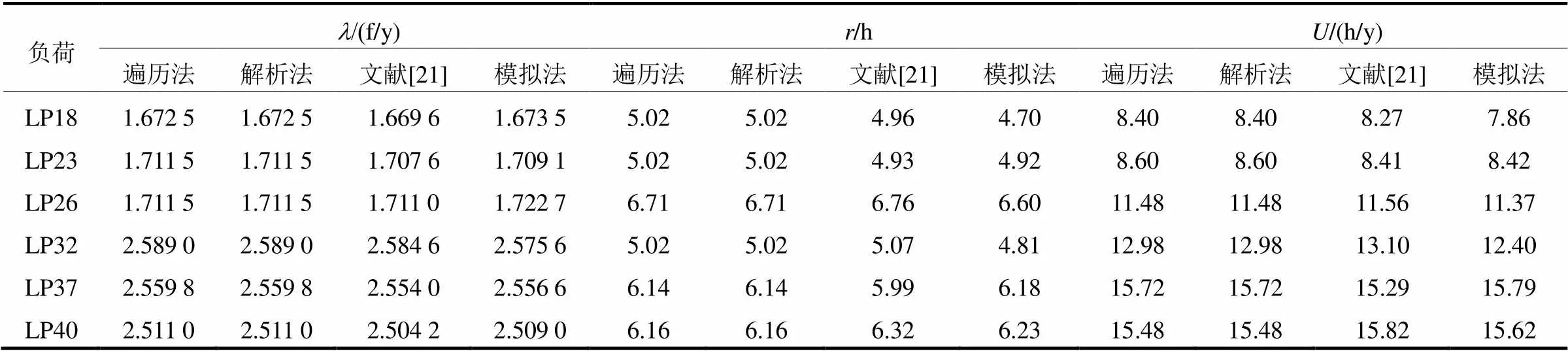
Table 1 Part load point reliability indices

表1结果表明，本文解析法与遍历法计算结果完全相同，模拟法与文献[21]以及解析法计算结果基本一致，验证了算法的正确性。

为比较同一类型算法在同一软件中的计算时间，给出遍历算法和本文解析法的计算时间如表2所示。

表2典型算例计算时间

Table 2 Computing time of typical example

从表2中计算时间可知，本文算法可靠性评估速度较传统算法有较大的提高。

部分负荷年停电频率的概率分布如图3所示。对辐射状配电网，离电源越近的负荷点年停电次数为0、1、2次的概率越大，可靠性越好，与负荷年平均故障率计算结果一致。

分别计及开关故障、变压器备用、熔断器不可靠熔断概率对系统可靠性指标的影响，与上述4种算法下的系统指标对比如表3所示。

表3系统可靠性指标

Table 3 System reliability indices

对比基本评估结果与其他各项计算结果可知：增加变压器备用，系统的停电频率指标基本不变，系统以及用户年平均停电时间大大减小，从而有效地降低了系统的缺供电量，提高了系统的供电可用率；熔断器可靠熔断概率对系统可靠性影响较大，熔断器可靠熔断的概率越小，配电系统可靠性越差；由于开关数目较少并且故障率较小，线路开关故障对系统停电频率和停电时间影响均不大。

采用2.3节贝叶斯诊断推理，统计典型负荷与系统的薄弱环节，取前5项如表4所示。

表4典型负荷及系统薄弱环节

Table 4 Typical load point and system weaknesses

根据表4结果可知，负荷的薄弱环节均为负荷支路上的变压器，这是因为负荷点薄弱环节是故障率与修复时间乘积最大的元件，而变压器的故障修复时间为200 h，故障率为0.015。线路35在大部分典型负荷的薄弱环节中，因此必定是整个系统最薄弱环节。

为验证薄弱环节辨识的正确性，将线路35、40、48的故障率置零，系统可靠性指标计算结果如表5所示。

表5系统可靠性指标的比较

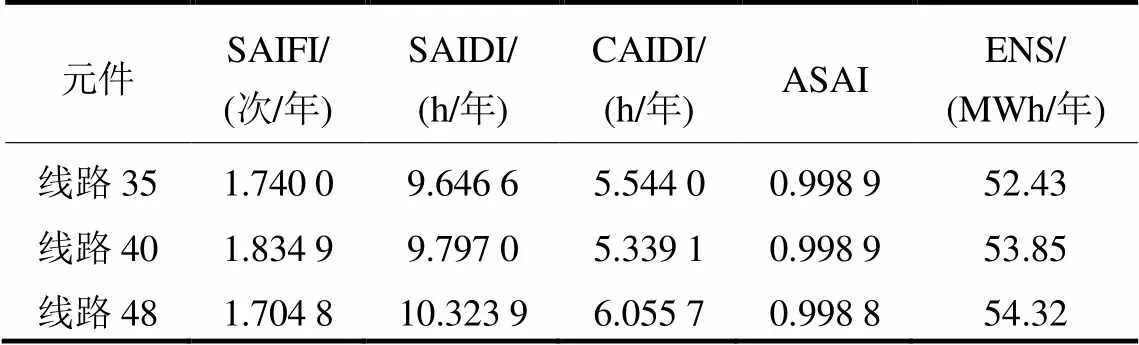
Table 5 Comparison of system reliability indices

由表5结果可知，改善线路35的可靠性参数对整个配电网可靠性的效果最显著，而改善线路48的可靠性参数对配电网系统平均停电频率的效果最佳，这是因为线路48是该系统中故障率最大的元件。然而由于其在配电系统中的位置靠近线路末端，部分负荷在其故障后可以通过切换开关恢复供电，因此分摊的缺供电量并不是最大，不是配电系统最薄弱环节，以上结果验证了薄弱环节分析的正确性和有效性。

4  结语

1) 对配电系统分区建立支路连接矩阵，可以减小连接矩阵的规模，节省存储空间；

2) 采用馈线分级和开关分层，可快速确定元件故障时保护动作开关的位置；

3) 结合动作开关顺序和位置，根据负荷与电源之间的连接通路判断负荷故障类型，有效地避免系统遍历，简化评估过程；

4) 将贝叶斯网络算法与蒙特卡罗模拟法相结合，可有效地辨识薄弱环节。

[1] 张鹏, 王守相. 大规模配电系统可靠性评估的区间算法[J]. 中国电机工程学报, 2004, 24(3): 77-84.

ZHANG Peng, WANG Shouxiang. A novel interval method for reliability evaluate on large scale distribution system[J]. Proceedings of the CSEE, 2004, 24(3): 77-84.

[2] BILLINTON R, BILLINTON J. Distribution system reliability indices[J]. IEEE Transactions on Power Delivery, 1989, 4(1): 561-568.

[3] 赵洪山, 赵航宇. 考虑元件故障率变化的配电网可靠性评估[J]. 电力系统保护与控制, 2015, 43(11): 56-62.

ZHAO Hongshan, ZHAO Hangyu. Distribution system reliability analysis considering the elements failure rate changes[J]. Power System Protection and Control, 2015, 43(11): 56-62.

[4] 苏傲雪, 范明天, 李仲来, 等. 计及风力发电影响的配电系统可靠性评估[J]. 电力系统保护与控制, 2013, 41(1): 90-95.

SU Aoxue, FAN Mingtian, LI Zhonglai, et al. Reliability evaluation of distribution system considering wind power effect[J]. Power System Protection and Control, 2013, 41(1): 90-95.

[5] 葛少云, 张鑫, 刘洪, 等. 基于点估计法的有源配电网概率可靠性评估[J]. 电力系统保护与控制, 2014, 42(12): 91-100.

GE Shaoyun, ZHANG Xin, LIU Hong, et al. Active distribution network probabilistic reliability evaluation based on point estimation method[J]. Power System Protection and Control, 2014, 42(12): 91-100.

[6] 赵洪山, 赵航宇. 考虑元件故障率变化的配电网可靠性评估[J]. 电力系统保护与控制, 2015, 43(11): 56-62.

ZHAO Hongshan, ZHAO Hangyu. Distribution system reliability analysis considering the elements failure rate changes[J]. Power System Protection and Control, 2015, 43(11): 56-62.

[7] 宁光涛, 严超, 朱思睿, 等. 一种发电系统可靠性评估的混合加速算法[J]. 电网与清洁能源, 2014, 30(11): 1-6, 13.

NING Guangtao, YAN Chao, ZHU Sirui, et al. A hybrid accelerated algorithm for generation system reliability evaluation based on sequential Monte Carlo simulation[J]. Power System Clean and Energy, 2014, 30(11): 1-6, 13.

[8] 李蓉蓉, 陈曦, 吴延琳, 等. 基于状态转移的高压直流输电系统可靠性分析[J]. 高压电器, 2015, 51(12): 66-71, 78.

LI Rongrong, CHEN Xi, WU Yanlin, et al.Reliability Analysis of HVDC transmission system based on state transition[J]. High Voltage Apparatus, 2015, 51(12): 66-71, 78.

[9] BILLINTON R, BILLINTON J. Distribution system reliability indices[J]. IEEE Transactions on Power Delivery, 1989, 4(1): 561-568.

[10] BROWN R E, GUPTA S, CHRISTIE R D, et al. Distribution system reliability assessment using hierarchicalMarkov modeling[J]. IEEE Transactions on Power Delivery, 1996, 11(4): 1929-1934.

[11] BILLINTON R, WANG P. Reliability network equivalent approach to distribution system reliability evaluation[J]. IEE Proceedings of Generation Transmission and Distribution, 1998, 145(2): 149-153.

[12] 吴素农, 吴文传, 张伯明. 考虑传输容量约束的配电网可靠性快速评估[J]. 电网技术, 2009, 33(14): 21-25.

WU Sunong, WU Wenchuan, ZHANG Boming. An efficient reliability evaluation method for distribution system with transmission capacity constraints[J]. Power System Technology, 2009, 33(14): 21-25.

[13] 祁彦鹏, 张焰, 余建平, 等. 配电系统可靠性分析的最小割集-网络等值法[J]. 电力系统及其自动化学报, 2011, 23(2): 98-104.

QI Yanpeng, ZHANG Yan, YU Jianping, et al. Application of minimum-cut set and network-equivalent method in distribution system reliability analysis[J]. Proceedings of the CSU-EPSA, 2011, 23(2): 98-104.

[14] 王秀丽, 罗沙, 谢绍宇, 等. 基于最小割集的含环网配电系统可靠性评估[J]. 电力系统保护与控制, 2011, 39(9): 52-58.

WANG Xiuli, LUO Sha,XIE Shaoyu, et al. Reliability evaluation of distribution systems with meshed network based on the minimum-cutset[J]. Power System Protection and Control, 2011, 39(9): 52-58.

[15] 郭飞, 陈炳华, 相中华. 基于递归算法的复杂辐射状配电网可靠性计算[J]. 电力系统保护与控制, 2010, 38( 5): 51-55.

GUO Fei, CHEN Binghua, XIANG Zhonghua. Computation of reliability in radial distribution network based on recursive algorithm[J]. Power System Protection and Control, 2010, 38(5): 51-55.

[16] 王光强, 谢开贵, 胡博, 等. 中压配电网可靠性评估的级别树算法[J]. 电网技术, 2011, 35( 12): 77-82.

WANG Guangqiang, XIE Kaigui, HU Bo, et al. A reliability level tree algorithm for reliability evaluation of medium voltage distribution networks[J]. Power System Technology, 2011, 35(12): 77-82.

[17] 彭建春, 何禹清, 周卓敏, 等. 基于可靠性指标逆流传递和顺流归并的配电网可靠性评估[J]. 中国电机工程学报, 2010, 30(1): 40-46.

PENG Jianchun, HE Yuqing, ZHOU Zhuomin, et al.Distribution system reliability evaluation based on up-streamdelivering and down-stream merging of reliability indices[J]. Proceedings of the CSEE, 2010, 30(1): 40-46.

[18] 霍利民, 朱永利, 张立国, 等. 用于电力系统可靠性评估的贝叶斯网络时序模拟推理算法[J]. 电工技术学报, 2008, 23(6): 89-95.

HUO Limin, ZHU Yongli, ZHANG Liguo, et al. Bayesian network time-sequence simulation inference algorithm for reliability assessment of power systems[J]. Transactions of China Electrotechnical Society, 2008, 23(6): 89-95.

[19] 许丹, 唐巍. 基于区域可达性分析的复杂配电网可靠性评估[J]. 电工技术学报, 2011, 26(6): 172-178.

XU Dan, TANG Wei. Reliability evaluation of complex for distribution networks based on regional accessibility analysis[J]. Transactions of China Electrotechnical Society, 2011, 26(6): 172-178.

[20] BAE I S, KIM J O. Reliability evaluation of customers in a microgrid[J]. IEEE Translations on Power Systems, 2008, 8(23): 1416-1422.

[21] 姚李孝, 赵兵, 伍利, 等. 基于混合算法的复杂配电系统可靠性评估[J]. 电力系统及其自动化学报, 2006, 18(6): 96-101.

YAO Lixiao, ZHAO Bing, WU Li, et al. Hybrid method for the reliability evaluation of complex power distribution system[J]. Proceedings of the CSU-EPSA, 2006, 18(6): 96-101.

[22] ALLAN R N, BILLINTON R, SJARIEF I, et al. A reliability test system for educational purposes-basic distribution system data and results[J]. IEEE Transactions on Power Systems, 1991, 6(2): 813- 820.

[23] BILLINTON R, JONNAVITHULA S. A test system for teaching overall power system reliability assessment[J]. IEEE Transactions on Power Systems, 1996, 11(4): 1670-1675.

(编辑 魏小丽)

Hybrid algorithm for reliability evaluation of distribution network based on element hierarchy and power accessibility

HU Meiyu, HU Zhijian, DENG Aopan, WANG Xiaofei, WANG Xiang

(School of Electrical Engineering, Wuhan University, Wuhan 430072, China)

This paper proposes a new reliability evaluation method for distribution system to solve the problem of repeatedly passing through the network topology.Element blocks and load blocks are established with switches as the boundary. Element level and switch hierarchy are proposed to determine the location of the protection elements, which can be combined with highly sparse equivalent branch connection matrix to fast analyze the accessibility between load and power or backup power to establish equivalent load failure result type list. Then the failure element is simulated in MCS and by analyzing which block it belongs to determine the type of load, the failure frequency and the failure duration time are counted to calculate reliability indices. The weak parts of load points and system are identified through the failure time and the failure power supply of related component. The reliability assessment results of the example show that the algorithm can correctly and efficiently calculate the reliability index and is suitable for complex distribution system reliability assessment.

This work is supported by the Specialized Research Fund for Doctoral Program of Higher Education of China (No. 20110141110032).

reliability assessment; element level; switch hierarchy; accessibility analysis; weak parts

10.7667/PSPC151056

2015-06-24；

2015-08-04

胡美玉(1990-)，女，硕士研究生，主要从事含DG的配电网优化运行、电力系统规划运行的研究；E-mail: 850488263@qq.com

胡志坚(1969-)，男，通信作者，博士，教授，博士生导师，研究方向为电力系统稳定分析与控制，新能源与分布式发电；E-mail: zhijian_hu@163.com

邓奥攀(1992-)，男，硕士研究生，主要从事电力系统可靠性分析研究。E-mail: 359705949@qq.com

高等学校博士学科点专项科研基金项目(20110141110032)