基于受电弓框架模型的部件危险点动应力计算方法

宋冬利, 江亚男, 张卫华, 梅桂明

(1.西南交通大学 牵引动力国家重点实验室, 四川 成都　610031；2.中国中铁科学研究院有限公司，四川 成都　611731)

服役时的受电弓处于高频振动状态，其部件产生疲劳裂纹甚至发生断裂[1-3]的故障屡见不鲜。开展受电弓疲劳可靠性的研究，一方面能掌握部件的疲劳寿命特性，制定合理的检修和更换周期；另一方面也是新产品开发的重要一环，对研制具有我国自主知识产权的新型受电弓具有重要意义。

受电弓疲劳可靠性研究的关键问题之一在于准确而高效地获取部件的动应力。目前已有研究者采用线路试验获取受电弓的动应力[2-3]，但线路试验费用昂贵、周期长，且测试数据受限于试验路段，另外设计阶段也没有实物可供线路试验，因此研究并完善受电弓动应力的数值计算方法很有必要。有限元法因其计算精度高、对复杂结构的适应性好等优点在疲劳应力计算方面得到了广泛的认可。Schulz和Nowack阐述了有限元法在结构疲劳应力分析中的重要价值[4]；英国标准BS 5400将有限元法作为疲劳应力分析的一种方法进行推荐[5]；由于有限元法在铁道车辆车体[6]、构架[7]、接触网[8]、桥梁[9]等领域的疲劳应力计算方面均有应用，因此宋冬利等在进行V500型受电弓疲劳可靠性设计[10]和考虑参数时变的TSG19型受电弓可靠性分析[11]时，采用了有限元瞬态分析法计算部件的动应力。有限元法在求解结构疲劳应力问题上的应用可归为2类：一类是通过静分析确定应力与载荷的映射关系，进而将动载荷换算成动应力；另一类是直接对结构进行瞬态分析。但前者忽略了惯性力和阻尼的作用，算法简单，只适合刚性较大且振动较小的系统；而后者虽能给出高精度的动应力计算结果，但其计算量较前者大得多。由于受电弓系统的上框架及以上部分具有良好的柔性，且部件振动加速度大，其惯性力无法忽略，因此第1类方法对该系统不适用。宋冬利等采用瞬态分析法计算受电弓动应力时，遇到计算效率较低，且在计算里程较长时难以收敛(稳定收敛里程约为3跨)等问题。

基于以上分析，本文根据受电弓结构多为规则截面杆件的特点，提出1种受电弓动应力计算的数值方法——PDSNA法(Numerical Algorithm for Pantograph Dynamic Stress)，并以瞬态分析法的计算结果为依据对本文方法的有效性进行验证。

1　PDSNA方法

PDSNA法是一种基于受电弓框架模型的动应力数值计算方法，通过建立受电弓的运动微分方程，计算受电弓规则截面任意点处的动应力，根据任意点处的动应力与危险点处动应力的映射关系，实现受电弓各部件危险点处动应力的计算。

1.1　受电弓运动微分方程

受电弓分为单臂和双臂2种，其中双臂受电弓由于维护成本较高以及容易在故障时拉断接触网而逐渐被淘汰，目前我国现役的高速铁路用受电弓均为单臂受电弓。单臂受电弓各部件多为规则截面，可简化为由杆件、质量块、弹簧和阻尼组成的框架模型，如图1所示。图中：AD杆为下臂杆；BC杆为拉杆；CDE杆为上臂杆；点E为平衡臂；质量块H为弓头；Fc为弓网接触压力；Fa为气动抬升力，且Fa=0.000 97v2(v为运行速度)；坐标系oxyz固结于A点，其中x轴为轨道纵向，y轴为竖直方向，z轴为轨道横向。

图1　受电弓框架模型

忽略横向偏移的影响，受电弓框架模型包含2个自由度，分别为AD杆绕z轴转动的自由度和质量块H沿y轴运动的自由度。其运动微分方程[12]为

(1)

其中，

式中：mH为弓头质量；FH为悬挂装置传递的作用力；C1，C2，…，C6为受电弓框架部分的拉格朗日方程系数；yH为质量块H的y向位移；yE为点E的y向位移；α为AD杆与x轴的夹角；KH，δH，BH分别为弓头悬挂的刚度、阻尼和干摩擦系数；g为重力加速度。

1.2　基于达朗贝尔原理的规则截面动应力计算

根据达朗贝尔原理，运动物体在惯性力和外载荷作用下可达到动态力平衡。图2(a)为AD杆的动态平衡力系。由图可见，AD杆绕z轴作定轴转动，转动角度为α；铰点A受铰点约束力FAx，FAy和约束力矩MAz的作用；铰点D受铰点约束力FDx和FDy的作用；质心P点受其自身重力G的作用；杆身惯性力为切向力FIt、法向力FIn和力矩MI；升弓装置提供的升弓力矩为MK。

根据达朗贝尔原理，建立AD杆动态平衡方程为

(2)

式中：m为AD杆质量；lAP为质心P距铰点A的距离；lAD为AD杆的长度；J为AD杆转动惯量。

设点D1为AD杆上的任意一点，则D1处截面的内力为轴力FND1、剪力FSD1和弯矩MD1(见图2(b))。建立AD杆局部坐标系ox1y1z，其中x1轴为平行点D1处截面方向，y1轴为AD杆轴线方向，则根据达朗贝尔原理得到点D1处截面的内力为

(3)

式中：lAD1为点D1距铰点A的距离；ρ为材料密度；A为截面面积。

图2　AD杆受力分析

AD杆的规则截面段为薄壁圆筒形，圆筒各点受沿AD杆轴线方向的正应力σ和平行于横截面的切应力τ，应力分布如图3所示。

根据材料力学理论，截面上任意一点的正应力σ和切应力τ分别为

(4)

(5)

式中：Iz为截面对中性轴的惯性矩；Sz为截面静矩；b为过x1位置作z轴平行线交圆筒截面实心部分的长度之和。

图3　AD杆规则截面的应力分布

受电弓其余部件规则截面的动应力计算过程与AD杆相似，限于篇幅此处不做详述。

1.3　应力映射关系

对于大型复杂结构，只需知道载荷类别和加载方式，即可以借助数值计算方法建立不同采样点之间的应力互推关系[13]。受电弓系统在载荷向量F(弓网接触压力，气动抬升力，重力)作用下，按照各载荷分量等比例加载，通过数值拟合得到多组不同载荷值工况下部件危险点R处的应力σR与规则截面任意点Q处的应力σQ的映射关系，为

σR=φ(σQ)

(6)

1.4　PDSNA方法数值计算流程

基于MATLAB软件实现PDSNA方法的数值求解，其流程如图4所示。其中，求解受电弓框架模型运动微分方程时，在求解时间中增加1个时间步长Δt，则t1=t+Δt时刻的运动参数迭代式为

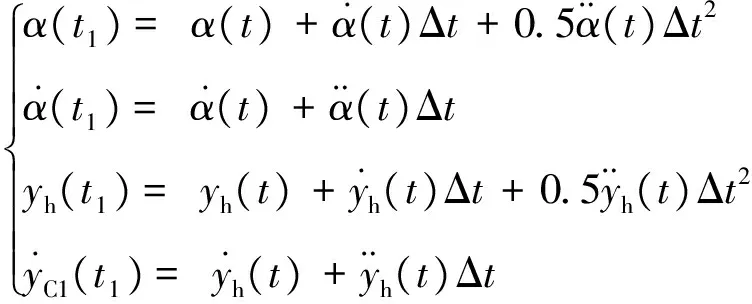
(7)

图4　PDSNA方法计算流程

2　有效性验证

本文以V500型新型受电弓[10,14]为例，分别采用有限元的瞬态分析法和PDSNA方法计算受电弓框架部件(下臂杆、拉杆、上臂杆和平衡臂)的动应力，通过对比2种方法的计算结果验证PDSNA方法的有效性。

2.1　受电弓有限元模型

利用ANSYS Workbench建立V500型受电弓的三维实体有限元模型，有限元建模过程参见文献[14]。考虑到本文分析工况，弓头顶部约束设为自由，并施加弓网接触压力Fc，受电弓运行过程中的气动抬升力Fa施加于滑板底部，V500型受电弓部件的铰接设置如图5所示，建立的三维实体有限元模型如图6。

图5　V500型受电弓部件的铰接设置

图6　V500型受电弓三维实实体有限元模型

2.2　危险点与规则截面点的应力映射关系

基于ANSYS Workbench的静强度分析功能，确定受电弓各部件在不同载荷值下危险点与规则截面点的应力映射关系。以受电弓AD杆和CDE杆为例，分析危险点与规则截面点的应力映射关系。

图7为V500型受电弓AD杆和CDE杆在某载荷值下的应力云图。

图7　V500型受电弓部件的应力云图

由图7可见，V500型受电弓AD杆和CDE杆的危险点分别为点132471和点114610。

任意选取AD杆的节点138693、CDE杆的节点115556为规则截面的应力计算点，进行多组载荷值工况的静强度计算，提取危险点和规则截面计算点的应力值，通过曲线拟合构建二者的映射关系，结果如图8所示。

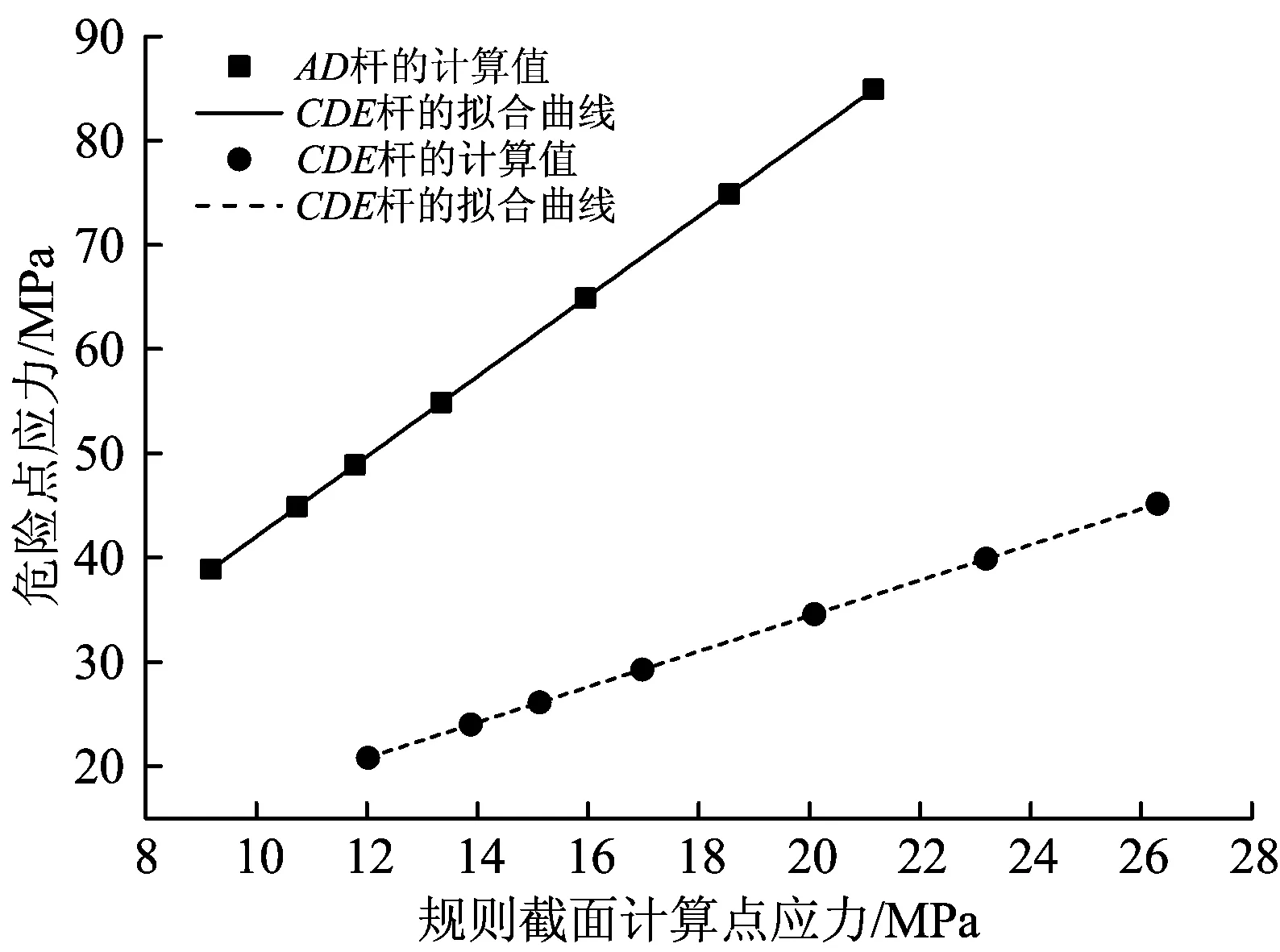
图8　危险点和规则截面计算点应力数据拟合

根据图8中的拟合曲线，得到AD杆和CDE杆上危险点应力(σRAD,σRCDE)与规则截面计算点应力(σQAD,σQCDE)的映射关系为

(8)

2.3　计算结果对比

分别采用有限元瞬态分析法和PDSNA方法，计算在图9所示时长为1.08 s(3跨)弓网接触力作用下的部件危险点动应力，图10为铰点A处的约束力和CDE杆危险点动应力对比结果；4.32 s(12跨)即长里程CDE杆危险点的动应力如图11所示；CDE杆长、短里程动应力幅频特性曲线如图12所示；各部件危险点的动应力计算结果见表1。

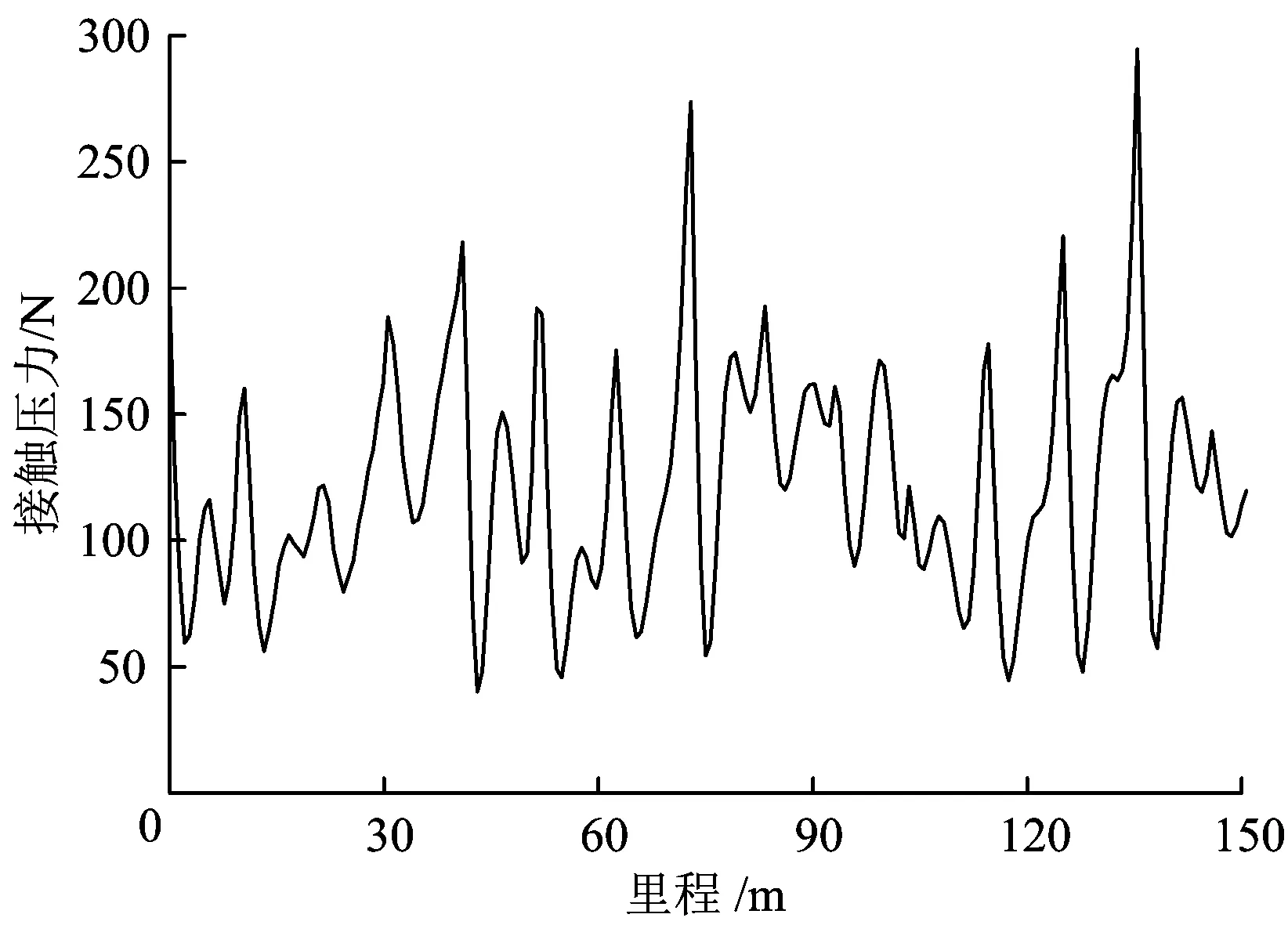
图9　弓网接触力(3跨)

图10　不同方法的计算结果对比

图11　长里程时CDE杆动应力时程曲线(12跨)

图12　CDE杆长、短里程动应力幅频特性曲线

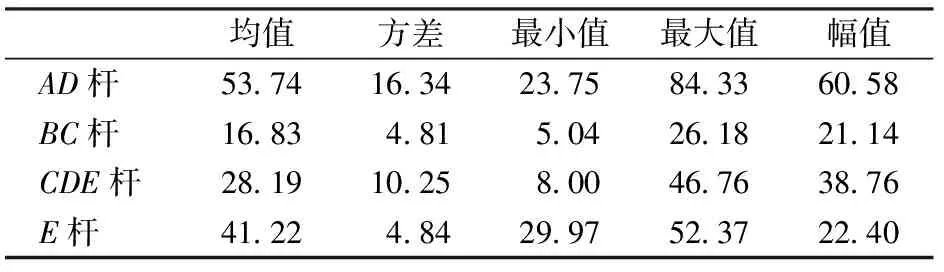
MPa

由计算结果可见，V500型受电弓的动应力最大值和幅值最大的部件为AD杆，CDE杆有较大的动应力幅值，BC杆和E杆的动应力幅值相当，E点的动应力均值大于BC杆的；用PDSNA法得到的铰点约束力和危险点动应力计算结果均与有限元的瞬态分析法吻合良好，这表明PDSNA方法是有效的；这2种方法在同一台计算机上运行，瞬态分析法耗时约为36 h，PDSNA法约为0.25 h，PDSNA法在计算效率上明显优于瞬态分析法；受结构复杂程度和计算量的影响，瞬态分析法的稳定收敛里程约为3跨，PDSNA法在1个锚段(约10～15跨)内仍能以较快的速度收敛，因此本文方法能够实现对受电弓长里程运行的动应力计算；对比CDE杆长、短里程的动应力幅频特性曲线可见，长里程动应力数据包含更丰富的频率信息，能够提高受电弓疲劳寿命预测结果的可信度。

3　结　论

(1) 本文根据受电弓部件多为具有规则截面的杆件这一特点，提出了基于受电弓框架模型的PDSNA动应力计算方法。首先建立由杆件、质量块、弹簧和阻尼构成的受电弓框架模型，通过求解框架模型运动微分方程得到各部件运动参数；然后基于达朗贝尔原理推导部件内力计算公式，并根据材料力学理论计算内力对应的规则截面动应力；最终根据规则截面计算点与危险点的应力映射关系，实现危险点的动应力计算。本文基于MATLAB软件实现了PDSNA方法的数值求解。

(2) 通过对比PDSNA方法和有限元瞬态分析法的计算结果表明，PDSNA方法的计算精度满足要求，在计算速率和计算样本容量上明显优于有限元瞬态分析法，计算结果包含更丰富的频率及接触网结构信息，这使下一步的受电弓疲劳寿命预测分析的可信度得以提高。

(3) V500型受电弓框架部件动应力计算结果表明，该型弓的下臂杆为动应力最大值和幅值最大的部件，上臂杆有较大的动应力幅值，拉杆和平衡臂的动应力幅值相当，平衡臂的动应力均最值大于拉杆的。

[1]涂建国, 胡海丽, 黄凤,等. 受电弓拉杆断裂失效分析[J]. 热处理技术与装备, 2014, 35(5):30-33.

(TU Jianguo，HU Haili，HUANG Feng，et al. Fracture Failure Analysis of Pantograph Rod[J]. Rechuli Jishu Yu Zhuangbei，2014, 35(5):30-33. in Chinese)

[2]李明高, 杨永勤, 宿崇,等. 高速动车组受电弓上臂横梁部件抗疲劳性能[J]. 大连交通大学学报, 2013, 34(4):23-27.

(LI Minggao, YANG Yongqin, SU Chong, et al. Research on Anti-Fatigue Performance of Upper-Arm Cross Beam of Pantograph Structure of Electric Multiple Units[J]. Journal of Dalian Jiaotong University, 2013, 34(4):23-27. in Chinese)

[3]李英, 徐练, 李明高,等. 高速动车组受电弓上臂顶管裂纹的分析及改进[J]. 机车电传动, 2014(3):110-112.

[4]SCHULZ U, NOWACK H. Significance of Finite Element Methods (FEM) in Fatigue Analyses[C] //Proceedings of the 6thInternational Fatigue Conference. Oxford: Pergamon, 1996:1057-1068.

[5]英国标准学会.钢桥、混凝土桥及结合桥[M]．成都：西南交通大学出版社，1986.

(British Standards Institution. Steel, Concrete and Composite Bridges[M]. Chengdu: Southwest Jiaotong University Press,1986.in Chinese)

[6]缪炳荣, 张卫华, 肖守讷,等. 机车车辆车体结构动应力计算方法[J]. 交通运输工程学报, 2007, 7(6):17-20，40.

(MIAO Bingrong, ZHANG Weihua, XIAO Shoune, et al. Dynamic Stress Calculation Method of Locomotive and Vehicle Carbody Structures[J]. Journal of Traffic & Transportation Engineering, 2007, 7(6):17-20，40. in Chinese)

[7]卢耀辉. 铁道客车转向架焊接构架疲劳可靠性研究[D]. 成都：西南交通大学, 2011.

(LU Yaohui. Study on Fatigue Reliability of Welded Bogie Frame for Railway Vehicle[D]. Chengdu: Southwest Jiaotong University,2011. in Chinese)

[8]刘怡, 张卫华, 梅桂明. 受电弓/接触网垂向耦合运动中接触网动应力研究[J]. 铁道学报, 2003, 25(4):23-26.

(LIU Yi, ZHANG Weihua, MEI Guiming. Study of Dynamic Stress of the Catenary in the Pantograph/Catenary Vertical Coupling Movement[J]. Journal of the China Railway Society, 2003, 25(4):23-26. in Chinese)

[9]李慧乐, 夏禾, 张楠,等. 基于车桥耦合动力分析的桥梁动应力计算方法[J]. 中国铁道科学, 2015, 36(1):68-74.

(LI Huile, XIA He, ZHANG Nan, et al. Calculation Method for Dynamic Stress of Bridge Based on Vehicle-Bridge Coupled Dynamic Analysis[J]. China Railway Science, 2015, 36(1):68-74. in Chinese)

[10]SONG Dongli, ZHANG Weihua, ZHOU Ning, et al. Fatigue Lifetime Design Method and Program Development of Pantograph V500 Based on Reliability[J]. Journal of Computers, 2012, 7(5)：1252-1260.

[11]SONG Dongli, ZHANG Weihua, HE Ping, et al. Reliability Analysis of TSG19-Type Pantograph Based on Time-Dependent Parameters[J]. Engineering Failure Analysis, 2013, 35(26):153-163.

[12]张卫华,沈志云.受电弓动力学研究[J]. 铁道学报，1993,15(1):23-29.

(ZHANG Weihua, SHEN Zhiyun. Dynamic Analysis of the Pantograph[J]. Journal of the China Railway Society, 1993, 15(1): 23-29. in Chinese)

[13]周宁,张卫华.基于互推的接触网腕臂系统动应力问题研究的新方法[J]. 铁道学报, 2008, 30(4): 16-21.

(ZHOU Ning, ZHANG Weihua. A New Inference-Based Method to Investigate Dynamic Stresses of Cantilever Structures of the Catenary System[J]. Journal of the China Railway Society, 2008, 30(4): 16-21. in Chinese)

[14]江亚男, 张卫华, 邹栋,等. 考虑风载的高速列车受电弓静强度分析[J]. 铁道机车车辆, 2014, 34(1):120-125.

(JIANG Yanan，ZHANG Weihua，ZOU Dong，et al. Static Strength Analysis of High Speed Pantograph Considering Aerodynamic Load[J]. Railway Locomotive & Car，2014, 34(1):120-125.in Chinese)