基于粒子群算法的阻抗控制在机械臂柔顺控制中的应用*
周晓东,任天助,张激扬,周 锐
(1.北京控制工程研究所 精密转动和传动机构长寿命技术北京市重点实验室,北京100190; 2.北京航空航天大学自动化科学与电气工程学院,北京100191)
基于粒子群算法的阻抗控制在机械臂柔顺控制中的应用*
周晓东1,任天助2,张激扬1,周 锐2
(1.北京控制工程研究所 精密转动和传动机构长寿命技术北京市重点实验室,北京100190; 2.北京航空航天大学自动化科学与电气工程学院,北京100191)
阻抗控制策略是实现机械臂的末端力柔顺控制的一种重要方法.然而,针对阻抗控制参数的确定,目前尚缺乏通用算法.粒子群算法具有概念简单、易行、鲁棒性好等特点,适用于阻抗控制参数的确定与优化.通过分析基于力反馈的笛卡尔空间阻抗控制结构,采用粒子群算法整定阻抗控制参数.结合阻抗控制自身特点对粒子群算法做了相应改进,并通过仿真验证了优化后的阻抗控制算法可实现对七自由度机械臂的柔顺控制且具有较好的鲁棒性.
粒子群算法;柔顺控制;阻抗控制;机械臂
0 引言
目前,应用于工业现场的机械臂只能完成一些固定轨迹的动作,如焊接、喷涂、搬运、码垛、普通装配及上下料等动作.这些工种对于机器人而言都属于结构化环境,被操作对象形状、位置及环境中的障碍物等信息是预知的,即实现预定轨迹的跟踪,属于单纯的位置控制.然而,对于某些精密装配、微操作、人机协调工作、空间机械臂对非合作目标的操控及移动式的服务机器人操作等工种,不仅要求机器人末端执行机构能到达预定位置,同时对操控力的柔顺性、安全性和平滑性要求日益提高.而传统的基于位置控制的工业机器人通常难以实现两个装配件的稳定接触.模型的不确定性和力反馈的缺乏可能导致较大的反作用力,甚至导致零件或机器人损坏.
基于此,近年来众多学者开展了关于机械臂力的柔顺控制研究[1-4].通过在机械臂的腕部、关节内部或手指等部位引入额外的力/力矩传感器实现力感知,再借助相应的控制策略实现对操控力的柔顺控制.归纳起来,针对机械臂的力控制,可分为两种:“力-位置”混合控制法和阻抗控制.其中,阻抗控制是将未知的环境等效为一个阻抗模型,将力控制转换为对位置控制的问题[5].该方法相对力-位置混合控制结构简单,但难于辨识阻抗控制器的阻抗参数.文献[6]针对双臂机器人的阻抗控制研究提出了一种自适应物体阻抗的方法并进行了稳定性证明,但未具体给出调节规律.文献[7]介绍了用阻抗控制的方法进行机械臂交互力控制,但其阻抗控制的参数是根据经验确定的.文献[8]采用自适应鲁棒控制策略,并对其阻抗参数进行寻优.其方法相对比较复杂,对于14个参数进行寻优的过程也并不经济.
本文采用粒子群算法进行寻优操作,并结合阻抗控制的特点对粒子群算法进行了一定程度的改进,使之更加适用于阻抗参数优化问题的求解.并以课题组的七自由度机械臂进行“销-孔”装配过程为例,采用仿真的方法,验证了该算法的有效性.
1 阻抗控制的原理与控制结构
1.1 阻抗控制的原理
1985年Hogan[5]率先提出阻抗控制的概念,其核心思想是将几乎所有的物理系统转化为如图1所示的“质量 -弹簧 -阻尼”系统,其受力情况可表示为

式中:ΔX=Xd-X,Xd为期望位置,X为实际位置.Kd为期望的刚度矩阵,Bd为期望的阻尼矩阵,Md为期望的惯量矩阵.由此可见,阻抗控制本身是一种将力控制转化为位置控制的方法.

图1 “质量-弹簧-阻尼”系统Fig.1 The“mass-spring-damper”system
阻抗控制从结构上可以分为基于位置的阻抗控制与基于力的阻抗控制[9],其主要区别在于后者是以位置信息作为反馈、力控制作为内环,前者是以末端受力信息作为反馈,位置控制作为内环.基于位置的阻抗控制策略在工程中获得了广泛的应用,本文将采用此方法进行研究.
1.2 基于力反馈的笛卡尔空间阻抗控制原理
图2为基于力反馈的笛卡尔空间阻抗控制原理[8]:将接触力误差 ΔF=Fd-Fe输入到阻抗控制器,得到笛卡尔空间的位置修正量 ΔX,将其用于对Xd进行修正,即可计算出位置控制量 Xc,进而得到关节转角控制量 θc,从而对机械臂实施位置控制.
由图3所示的机械臂腕部受力与销子末端接触力的示意图可知:图2中的末端接触力转化矩阵Te如式(2).其中L1、L2的物理意义如图3所示.
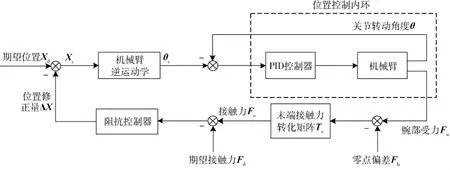
图2 基于力反馈的笛卡尔空间阻抗控制原理图Fig.2 The structure of a impedance control in Cartesian space based on force feedback

图3 销子末端接触力与腕部受力示意图Fig.3 The illustration of the pin’s contact force andthe manipulator’s wrist force

为了将式(1)应用于7-DOF机械臂的力阻抗控制系统,对其进行拉普拉斯变换可得

对式(3)阻抗参数Md、Bd、Kd进行整定优化,即可通过图2所示的控制原理,实现对机械臂的柔顺控制.
2 阻抗控制参数的优化模型
本文研究的对象为一台七自由度的冗余机械臂,其具体作业任务为机械臂抓持一个销子进行插孔操作,通过柔顺控制策略实现对销子末端与孔底部接触力的控制.
2.1 机械臂力反馈模型
为便于研究,本文做如下两点假设:
(1)销子与销孔间的接触力为单方向的,垂直于孔的底部平面,两者间不存在相对滑动或滑动趋势;(2)将销孔简化为弹簧模型,设其等效弹簧刚度系数为ke.

由假设(1)可知,该阻抗控制问题转化为一维的,此时式(1)可简化为式中,kd、bd、md为期望的阻抗参数,fe和 fd分别实际接触力及期望的接触力,δx为位置误差


式中,xd为销子末端的期望位置,x为其实际位置.则接触力方程实施柔顺控制策略时,式(6)中的等效弹簧刚度ke通过试验方法获得.具体方法为:设销子末端在x0处时刚好接触销孔底部平面,x1处时的接触力为f1,则

当接触力满足fe=fd时,即可实现对销子与孔接触力的柔顺控制.
2.2 阻抗控制器的设计
图4为本文所提出的阻抗控制器原理图,该控制器以ΔF(此处为一维,下同)作为输入,输出为位置修正量ΔX.

图4 阻抗控制器原理图Fig.4 Impedance controller diagram
3 基于粒子群的参数优化方法
3.1 基本粒子群算法设计
在寻优过程中,粒子群算法需根据目标函数确定各粒子的适应度,适应度函数的优劣决定寻优质量.一般而言,目标函数采用二次型.选取控制误差与输出能量综合起来最小的方向进行寻优

式中:e为控制误差、u表示控制器输出,分别对应2.2小节中的ΔF和ΔX;ρ1为常数,取值范围为0~1,根据需要设定.参数优化步骤如下:
(1)粒子群初始化
针对被优化的阻抗参数的整定问题,随机生成一群初始粒子,其数值分别对应阻抗参数中M、B、K,由于其大小根据仿真过程中设置的弹性模量决定,因此初始粒子的位置在一定范围内等概率分布.并设置最大迭代次数以及目标函数的最小值.
(2)更新每个粒子的速度与位置
按照式(9)和式(10)更新粒子的速度与位置

式中:w为权重因子;i=1,2,…,N为粒子种群中的各个粒子,k=1,2,…,kmax为粒子所处的代数,则 vki代表第i个粒子处于第k代时的速度,xki代表第i个粒子处于第k代时的位置;xpi为第 i个粒子至今为止的最好位置;xgi则代表至今为止整个种群的最好位置;c1和c2为加速常数,分别表征当代个体与代际群体的学习能力大小;nrand1与 nrand2是[0,1]的随机数.由式(9)、(10)可知:进化粒子的状态通过先前经验与随机过程进行更新.
(3)计算适应度
根据前文提到的目标函数衡量每个粒子的适应度.在阻抗控制问题中,目的是使得末端受力接近期望受力,故要使目标函数最小化.
(4)通过比较得出个体最优值与群体最优值
将每个粒子当代的适应度与该粒子之前的值作比较.若当代的粒子更具适应性,即在阻抗控制中适应度函数值更小,则将前代粒子进行替换.每个个体进行比较之后,选出这一代粒子中最适应环境的个体,作为这一代的全局适应度.若这一代的全局的适应度优于上一代,则更新当代全局适应度.
(5)算法更新循环
若不满足终止条件,重复步骤(2);当满足终止条件时,退出算法,得到最优解.终止条件为达到最优的目标函数值;如果始终无法达到,则在达到最大迭代次数时退出.
3.2 针对阻抗控制问题的改进
(1)适应度函数优化
对于阻抗控制,要保证系统达到稳态时末端受力满足期望值外,还须考虑系统达到稳态的过渡过程中,力的调整不宜过大.若在过渡过程中超过一定范围,势必会损坏机械结构,因此须对此进行限制,将力反馈的峰值作为适应度函数中的一部分,式(8)转化为
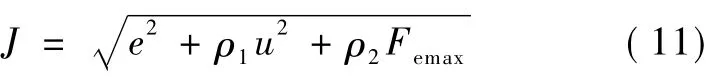
式(11)中Femax代表力反馈的峰值,ρ2为权值系数,在仿真实验中对其进行调整,使其起到作用,又不至于影响过大导致误差不能正常收敛到0.
(2)进行变异操作,防止算法过早陷入早熟
由式(9)可知:粒子下一刻的位置由当前位置与当前速度共同决定,其中粒子移动的速度跟每一代个体的最优位置xpi和整个种群的最优位置 xgi有关.然而,当粒子当前位置很接近一个局部最优值时,会表现出很强的趋同性[10],快速地收敛到一个历史最优值,陷入了“局部最优”.基于此,可采用变异的方法增强算法的全局搜索能力,克服收敛到局部最优的缺点.其变异机制如下:在每一次迭代中,满足式(12)变异条件的粒子将产生变异

式中:x(k)为第 k代迭代粒子适应度;x(bk)为至第k代粒子群最适应值;η为变异系数,用于判断粒子与最优值接近到何种程度时进行变异.
文献[10]采用多种变异公式根据概率选择变异机制,这种方法可显著地增加粒子的多样性,但设置不同变异公式的概率需要反复调节概率参数才能发挥最大优势.这与本文简化阻抗控制中参数调节的初衷相违背,因此采用简单随机变异

式中n代表0~1之间的随机数,x(k+1)、x(k+1)分别
randminmax为其可以选择的最大值与最小值,按照3.1小节中的步骤,将该步置于步骤(5)之前.
3.3 仿真实验
(1)七自由度机械臂插销过程建模
为了对整个阻抗控制系统进行验证,首先需建立机械臂“销-孔”装配模型(图5所示).由于获得机械臂的动力学模型不仅需要进行复杂的运动学正、逆解,且需对接触面进行力学建模.本文采用多体动力学仿真软件ADAMS和MATLAB进行联合仿真[11].将模型导入ADAMS并建立机械臂末端与环境间的接触.
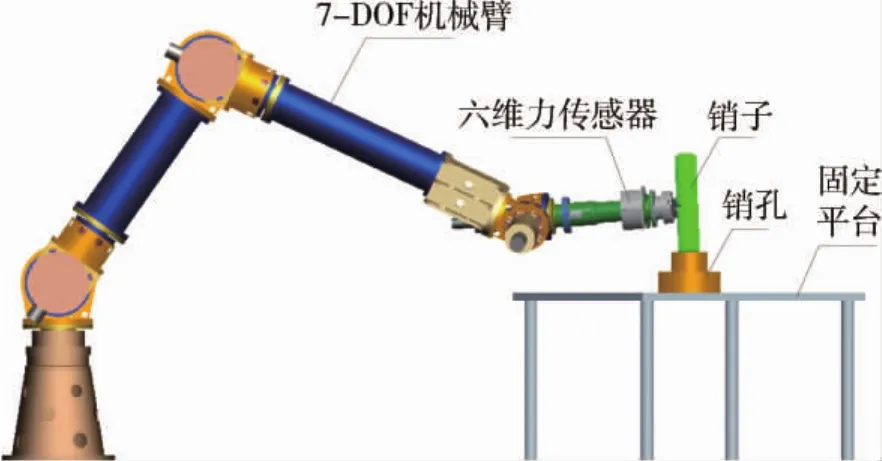
图5 七自由度机械臂“销-孔”装配三维模型Fig.5 A 3D model of the 7-DOF manipulator with“peg-in-hole”assembly
设机械臂末端握持的销子与孔为的材料的弹性模量为E=120 GPa,泊松比为ν=0.25.初始位置时,使销子末端与孔底平面刚好接触,接触部位无变形;然后使机械臂沿孔的轴线方向移动微小位移 δs,此时 ADAMS测得的接触力为 fc,由2.1小节可知

经仿真可知:ke=1.787 5×104N/mm.
(2)含有力反馈的闭环系统仿真过程
系统由一个开环结构和一个闭环结构组成.开环部分的作用是通过轨迹规划将销子从初始位置移动到孔口上方.销子到达指定位置后,插孔过程开始,此时启用力反馈,将ADAMS中计算的接触力值作为反馈量输入到阻抗模块.经计算得到应移动到的位置,再将该位置转化为关节坐标使机械臂运动.
(3)整定阻抗控制参数的仿真结果
设置阻抗控制的参数 M、B、K(单位分别为: (N·s2)/mm、(N·s)/mm和 N/mm)的初始范围为[0,100],粒子群规模为100,最大迭代次数为20,参数整定的结果如图6~8所示.
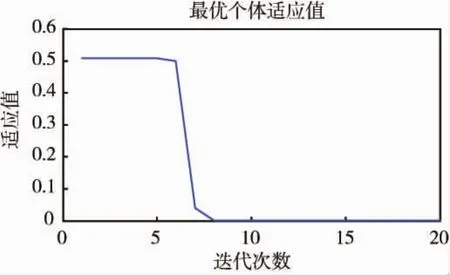
图6 最优个体收敛过程Fig.6 The process of optimal individual convergence

图7 阻抗参数收敛过程Fig.7 The convergence process of impedance parameter

图8 接触力变化曲线Fig.8 The variation of contact force
为便于验证算法,设插销过程中销子始终保持竖直,直到与孔底面接触,不受孔壁摩擦力的影响,设当销子与孔底面的接触力为200 N时,插销过程结束.由图7可知:这种改进的粒子群算法可以使参数收敛到适宜的值,最终得到的力反馈值平稳的达到期望值,未出现过大超调.
为进一步验证算法的鲁棒性,考虑将机械臂的位置控制内环,等效为一个理想的一阶惯性环节.实际操作是在原有的被控对象模型中串联一个一阶惯性环节,而不改变算法的其他设置.此时参数整定的结果如图9~11所示.

图9 考虑内环影响后最优个体收敛过程Fig.9 The process of optimal individual convergence with inner-loop

图10 考虑内环影响后阻抗参数收敛过程Fig.10 The process of impedance parameter convergence with inner-loop

图11 考虑内环影响的接触力变化曲线Fig.11 The variation of contact force with inner-loop
由此可见,即使在系统中引入一阶惯性环节,改进的粒子群算法依然可以使系统按照期望达到收敛.但值得说明的是其控制效果较之前有了比较大的超调,其原因在于该算法需要根据控制系统的不同及时调整粒子群算法中的有关参数,其鲁棒性与自适应性有待进一步提高.
4 结论
本文将阻抗控制方法与粒子群算法相结合,提出了基于粒子群算法优化的阻抗控制策略并将其应用于七自由度机械臂的力柔顺控制.针对基本粒子群算法的一些缺陷,进行了适应度函数的改进,并引入变异操作.仿真结果表明:基于粒子群算法的机械臂阻抗控制参数优化方法简化了繁琐的调参过程,控制效果良好且具有一定的鲁棒性.
本文的不足之处在于该方法不能在线确定阻抗参数,而是需要多次离线的仿真计算确定,会给工程应用带来不便.且只针对一维的阻抗参数做了整定和优化,后续研究将考虑实际的六维力情况,对多维阻抗参数进行在线整定并开展相关试验研究.
[1]FANNY F,LUIGI V,BRUNO S.Variable impedance control of redundant manipulators for intuitive human-robot physical interaction[J].IEEE Transactions on Robotics,2015,31(4):850-863.
[2]ETIENNE B,GOWRISHANKAR G,CHENGUANG Y,et al.Interaction force,impedance and trajectory adaptation:by humans,for robots[J].Springer Tracts in Advanced Robotics,2014,79(1):331-345.
[3]PAREDES M L,GONZALEZ de S P.Dataglove-based interface for impedance control of manipulators in cooperative human-robot environments[J].Measurement Science and Technology.2013,24(2):1-13.
[4]董晓星.空间机械臂力柔顺控制方法研究[D].哈尔滨:哈尔滨工业大学,2013.DONG X X.Research of compliance control strategies for space robotic arm[D].Harbin:Harbin Institute of Technology,2013.
[5]HOGAN N.Impedance control:an approach to manipulation[J].Journal of Dynamic Systems Measurement&Control,1985,107(1):1-24.
[6]周扬.双臂机器人的控制系统建立及阻抗控制研究[D].哈尔滨:哈尔滨工业大学.2014.ZHOU Y.Establishment of control system and research on impedance control for dual-arm robots[D].Harbin: Harbin Institute of Technology,2014.
[7]GEA J D,KIRCHNER F.Modelling and simulation of robot arm interaction forces using impedance control[J].World Congress,2008,17(1):15589-15594.
[8]JIANG Z H,KOHNO M.Robotic manipulation of flexible objects based on vibration control using force sensors[J].Systems,Man and Cybernetics,2002,4(5):363.
[9]ZENG G W,HEMAMI A.An overview of robot force control[J].Robotica.1997,15(5):473-482.
[10]王苗苗,高岳林.一种新的带有动态自适应惯性权重和混合变异的粒子群优化算法[J].计算机应用与软件,2010,27(6):70-72.WANG M M,GAO Y L.A new particle swarm optimization with dynamically adaptive inertia weight and hybrid mutation[J].Computer Applications and Software.2010,27(6):70-72.
[11]PAWLETTA T,FREYMANN B,DEATCU C,et al.Robotic control& visualization toolbox for MATLAB[J].IFAC-PapersOnLine,2015,48(1):687-688.
Application of Impedance Control for a Robotic Manipulator Based on Particle Swarm Optimization Algorithm
ZHOU Xiaodong1,REN Tianzhu2,ZHANG Jiyang1,ZHOU Rui2
(1.Beijing Key Laboratory of Long Life Technology for Precise Rotating and Transmission Mechanism,Beijing Institute of Control Engineering,Beijing 100190,China; 2.School of Automation Science and Electrical Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
Impedance control strategy is one of the most important methods for the force and compliance control of robotic manipulators.However,it is difficult to obtain impedance parameters due to the absence of versatile algorithms.According to the structure of Cartesian impedance control based on force feedback,Particle swarm optimization(PSO)algorithm is employed to determine and optimize the impedance parameters via taking advantage of its concision,feasibility and robustness.In addition,the PSO algorithm is improved to some extent in the characteristics of impedance control.Finally,the robustness performance of the optimized impedance control strategy is verified via simulation of compliance control of a 7 DOF(degree-of-freedom)robotic arm.
PSO;compliance control;impedance control;robotic manipulator
TP242.2
A
1674-1579(2016)03-0015-06
10.3969/j.issn.1674-1579.2016.03.003
周晓东(1983—),男,工程师,研究方向为智能机器人技术;任天助(1992—),男,硕士研究生,研究方向为机器人智能控制算法设计;张激扬(1970—),男,研究员,研究方向为航天器姿态测量和姿态控制执行机构;周 锐(1968—),男,教授,研究方向为飞行器制导与控制.
技专项资助项目(Z151100001615067).
2016-01-18

