基于视线测量和轨道预报高轨非合作目标相对导航方法*

张 杨，王典军，朱志斌，高恩宇

(1.中国空间技术研究院通信卫星事业部，北京100094;2.北京控制工程研究所，北京100190)

基于视线测量和轨道预报高轨非合作目标相对导航方法*

张 杨1，王典军1，朱志斌2，高恩宇1

(1.中国空间技术研究院通信卫星事业部，北京100094;2.北京控制工程研究所，北京100190)

对于非合作目标，由于中远距离星上相对测量手段有限，大多情况仅能获得视线角信息.仅视线测量相对导航方法在GEO轨道条件下滤波精度低、可观测性差.提出一种基于星间视线方位测量和轨道预报信息结合的非合作目标相对导航方法.建立基于星间相对运动模型的状态方程和基于星间视线测量和轨道预报信息的观测方程，分别选取了扩展卡尔曼滤波和无迹卡尔曼滤波两种方法，仿真分析了轨道预报信息精度和滤波方法对导航精度的影响.

相对导航;视线测量;扩展卡尔曼滤波;无迹卡尔曼滤波

0 引言

合作目标交会对接采用的成熟相对导航方法均依赖完整位置测量信息，非合作目标不具备GPS、应答机和激光角反射器等条件，特别对于中远距离，很难获得精确星间距离信息，但依靠光学相机和图像处理方法，可以获得准确的视线方位信息.文献［1］提出了近地轨道上仅依靠视线测量的非合作目标相对导航方法，但在中高轨道，由于测距信息缺失，利用仅视线测量的相对导航方法的可观性较差.

由于非合作目标地面定轨精度差，特别是轨道倾角矢量与标称值偏差较大，远距离引导段需要提高相对倾角的矢量确定精度，进而修正轨道面，保证在交班点处目标能够出现在追踪星的捕获相机视场内.本文提出一种基于星间视线角测量和轨道预报信息相结合的GEO轨道非合作目标相对导航方法，轨道预报信息中仅使用测距信息，推导基于轨道要素的两卫星相对轨道运动学及动力学模型，选用非线性卡尔曼滤波方法，进行仿真分析，验证导航方法的可行性，并讨论不同精度测距信息和滤波方法对导航精度的影响.

1 GEO轨道相对运动学及动力学模型

本文的研究对象为两个卫星(目标星和追踪星)的相对运动，参考坐标系选用地心惯性坐标系和卫星轨道坐标系，地心惯性坐标系原点O在地球质心，Z轴沿地球自转轴指向北极，X轴在地球赤道面内指向春分点;卫星轨道坐标系原点O'在卫星质心，Z'指向地球质心方向，Y'垂直于轨道平面，沿负法线方向.图1为两坐标系示意图，其中Ω为升交点赤经，i为轨道倾角，纬度幅角u=ω+f，ω为近地点幅角，f为真近点角.

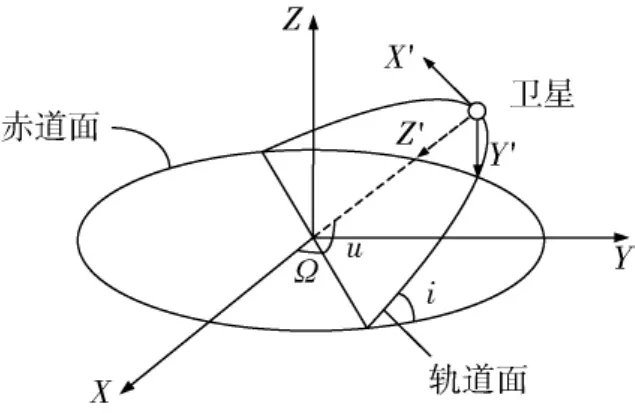
图1 惯性坐标系和轨道坐标系Fig.1 Inertial and orbit coordinates

1.1 基于相对轨道要素的卫星相对运动描述

本文考虑到自然运动相对轨道根数的5个变量均为缓慢变化，适于分析滤波稳定性，且空间几何意义清晰.定义卫星间的相对轨道要素为

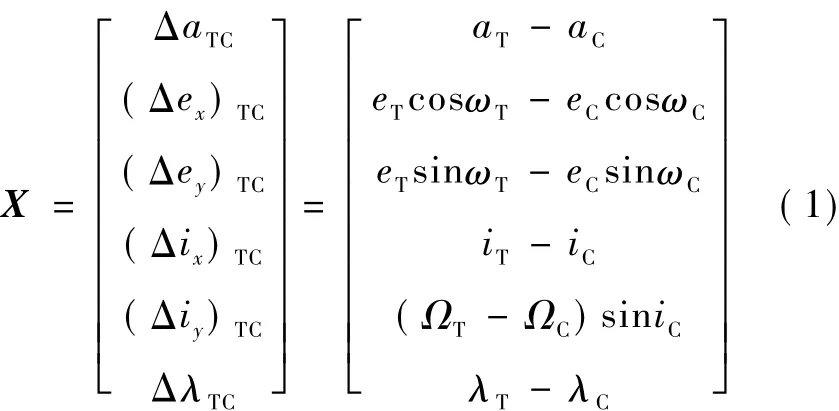
式中，a为半长轴，e为偏心率，λ为平纬度幅角.则卫星间的相对位置与相对轨道要素间的映射关系可以表示为

1.2 卫星轨道动力学模型

当考虑地球中心天体引力和二阶带谐摄动(J2项摄动)时，自然运动条件下，卫星含二阶带谐项的轨道动力学模型为

等式右侧阵为平均轨道要素随时间的长期变化率在近圆轨道条件下通过线性化得到的矩阵.

式中，J2表示摄动项系数，J2=1.082 63×10－3.

1.3 敏感器观测模型

定义观测量Δr、α、β，如图2所示.

图2 追踪星轨道坐标系及其观测变量Fig.2 Orbit coordinates of chase satellite and observed variables

Δr:目标星和追踪星之间的距离.

α:目标星在追踪星测量坐标系中的方位角，即追踪星与目标星连线在轨道坐标系XY平面的投影与X轴的夹角.沿Z轴负方向逆时针方向为正向.

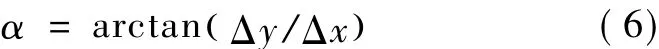
β:目标星在追踪星星测量坐标系中的俯仰角，即追踪星与目标星连线在轨道坐标系XY平面的投影与该连线的夹角.β与Δz的正负相反.

2 相对导航滤波算法

本文所研究的高轨卫星间相对导航滤波模型属于高斯非平稳随机过程，不能直接通过卡尔曼滤波进行估计，通常采用扩展卡尔曼滤波(EKF)方法［2］.文献［3］将 EKF算法用于导航滤波算法，得到了较好的结果，文献［4］提出了一种基于插值滤波的改进型 EKF算法，进一步提高了导航精度.EKF算法需要对非线性动力学模型和观测模型进行线性化处理［5］，在对系统进行泰勒展开时，若保留低阶项，则容易产生较大的截断误差，若保留较高阶数，则易使滤波器发散.基于无迹变换的无迹卡尔曼滤波(UKF)可以更好的估计非线性系统状态变量的均值和均方差，对于在高斯白噪声干扰下的非线性系统有着更好的估计精度，且不需要求雅克比矩阵，但需要更大的计算量［6］.

2.1 系统状态方程

根据式(1)，令

滤波估计中的系统方程可以表示为

式中，ξ=［ξΔaξΔexξΔeyξΔixξΔiyξΔλ］T为模型简化引起的系统误差，这里假设其满足零均值的高斯分布.对状态方程进行离散化处理式中，Xk为系统k时刻的状态向量，Φk+1，k为从 k时刻到k+1时刻的状态转移矩阵，为对应的正则化时间单位，aC为正则化长度单位，即目标星轨道半径.

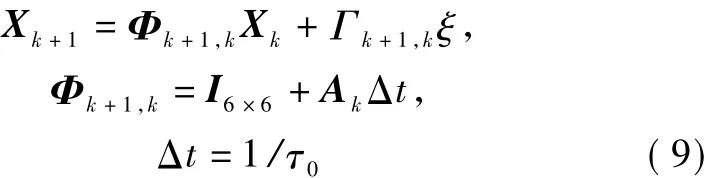
2.2 系统观测方程

观测方程可以表示为

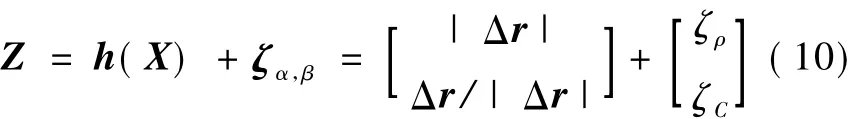
式中，Δr=［Δx Δy Δz］T为轨道预报得到的目标星在追踪星轨道坐标系下的相对位置，其与相对轨道要素间映射关系可以根据式确定.ζρ为相对距离的测量误差，由于测距信息通过对轨道预报信息提前处理获得，其常值误差和周期性误差可以在傅里叶变换后直接去掉，这里假设其满足零均值的高斯分布.ζC为单位视线矢量测量误差，假设其满足零均值的高斯分布，当误差较小时其协方差矩阵可以表示为

线性化处理可得观测方程的Jacobian矩阵

其中，

2.3 基于EKF算法的滤波器设计

根据Kalman滤波基本方程可得状态更新方程和测量更新方程

式中:Kk+1代表滤波增益矩阵;滤波初值和滤波误差

方差矩阵的初值分别为

以上为系统基于EKF算法的滤波器设计流程，关于EKF算法的详细介绍请参见文献［7］.

2.4 基于UKF算法的滤波器设计

将扩展Kalman滤波中统计特性传播方式的线性化近似用UT变换方法代替，即可得到无迹Kalman滤波.考虑之前定义的非线性系统，UKF的具体流程为初始化、计算 Sigma点 ξik－1(i=0，1，2，…，2n)、时间更新、观测更新、滤波更新几个过程.关于UKF算法的详细介绍请参加文献［8］.

3 仿真分析

设定追踪星在目标星后方约100 km处，轨道要素相差较小，表1给出了两卫星的初始平均轨道要素，其中ξ=ecosω，η=esinω.

表1 卫星初始平均轨道要素Tab.1 Initial mean orbital elements of satellite

目前卫星地面测控系统的定轨精度要求一般为(3σ):半长轴Δa≤100 m、偏心率 Δe≤6×10－6、轨道倾角 Δi≤0.005°、平经度Δλ≤0.005°.仿真时间为1.5×105s.目标星在追踪星轨道坐标系下的视线角测量精度 ζC为0.02°(±σ)，地面定轨相对距离测量精度 ζρ为1 km(±σ)、10 km(±σ)、50 km(±σ).状态变量误差协方差阵初值为 P0= 1×10－8diag{1，1，1，1，1，1}、系统随机噪声协方差阵为Q=1×10－16diag{0.01，0.05，0.1，0.01，0.01，1}及观测噪声协方差阵为R=diag{ζ2ρ，10－7，10－7，10－7}.

在不同距离测量精度条件下，分别使用基于EKF的滤波器和基于UKF的滤波器进行状态变量的估计.图3～5表示了不同测量精度下2种滤波算法对相对轨道要素的估计误差，这里用相对轨道要素误差与追踪星轨道半径的乘积来表示，单位km.图中虚线和实线表示基于EKF和UKF的相对轨道要素误差的估计结果.根据需求，相对距离100 km处，导航精度需小于2 km.

3.1 测距精度对滤波估计的影响

以EKF滤波算法为例.采用蒙特-卡洛法分别对测距精度为1 km、10 km、50 km 3种条件进行100次仿真，其中初始参数设定P、Q以测距精度为1 km收敛条件为准，其他情况只改变测距精度及观测方程系统噪声方差阵R，曲线收敛后，对估计误差求取期望和均方差，为了计算准确，取时间为3×104s时刻，结果如表2所示.

从表中可以得出，各轨道要素均满足导航精度要求.不同测距精度对相对估计误差的期望影响有限，但是随着测距精度的增加，部分相对估计误差的均方差增加，数据量级明显增大，说明误差带带宽增加，曲线不集中.如Δλ的误差期望变小，但均方差增大.

3.2 滤波算法对滤波精度的影响

从滤波时间和滤波精度两个方面来分析蒙特-卡洛法得出的仿真数据.采用测距精度为10 km的仿真条件，仿真时间分别取5 000 s，10 000 s，15 000 s和20 000 s 4个时刻进行采样，计算 EKF和UKF两种算法得出的相对轨道根数的期望和均方差分析滤波时间和滤波精度，结果如表3～4所示.

图3 相对轨道要素估计误差(测距精度1 km)Fig.3 Estimate error of relative orbital elements (range accuracy:1 km)

图4 相对轨道要素估计误差(测距精度10 km)Fig.4 Estimate error of relative orbital elements (range accuracy:10 km)

图5 相对轨道要素估计误差(测距精度50 km)Fig.5 Estimate error of relative orbital elements (range accuracy:50 km)

表2 不同测距精度下EKF滤波均方差与期望(t=30 000 s)Tab.2 Variance and expectation of EKF under different ranging accuracy(t=30 000 s) km

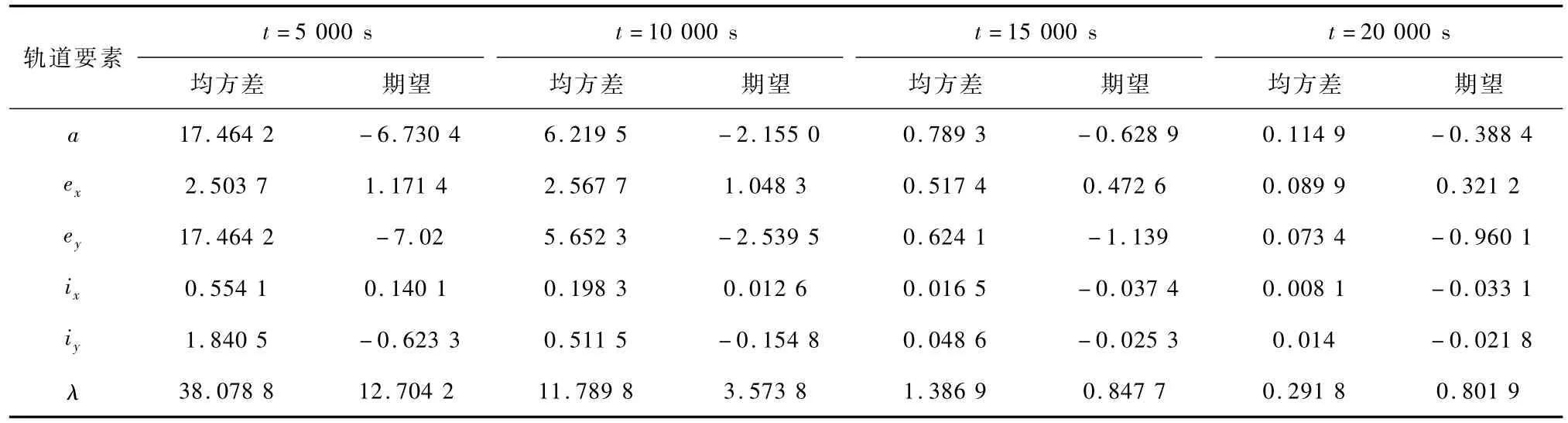
表3 EKF滤波均方差与期望(测距精度10 km)Tab.3 Variance and expectation of EKF(range accuracy:10 km) km

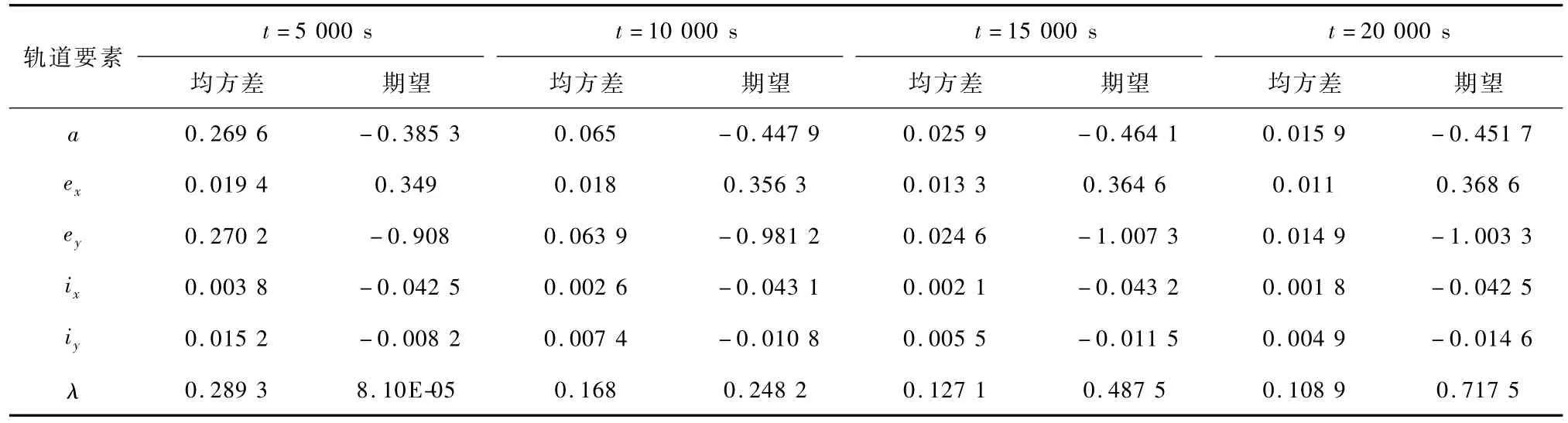
表4 UKF滤波均方差与期望(测距精度10 km)Tab.4 Variance and expectation of UKF(range accuracy:10 km) km

从表中可以看出，EKF算法期望在15 000 s稳定，均方差到20 000 s稳定;UKF算法期望在10 000 s已经接近稳定，均方差数值也远小于同一时刻EKF算法的均方差值，所以滤波收敛时间上UKF算法优于EKF算法;在滤波精度上，在20 000 s，两种算法期望量级差别在十米级，但EKF算法的均方差值全部大于UKF均方差值，数据相对分散，说明EKF滤波精度略低于UKF滤波精度.

4 结论

本文提出并通过仿真验证了一种基于星间视线测量和地面测距信息的GEO轨道非合作目标相对导航方法.

仿真分析结果表明:(1)导航方法具有递推和修正能力，满足导航需求;(2)地面测轨精度越低，导航精度越差;(3)UKF算法的仿真结果优于EKF算法的仿真结果，但UKF算法计算量较大，计算时间长，较难实现实时导航.在满足导航精度的前提下，可选择EKF算法作为星上自主相对导航算法.(4)导航方法可以实现对相对轨道倾角的高精度估计，估计结果可以作为追踪航天器进行轨道机动以减小与非合作目标轨道倾角的依据，对于解决交班点处目标脱离捕获相机视场的问题提供很大帮助.

［1］SIMONE D A.Autonomous formation flyingin low earth orbit［D］.Holand:Delft University of Technology，2010.

［2］GRASSIDIS J L，JUNKINS J L.Optimal estimation of dynamic systems［D］.New York:Chapman and Hall CRC，2004.

［3］王洋，曲长文，蒋波.低轨星座对自由段空间目标跟踪算法研究［J］.电子测量技术，2009，32:157-160.WANG Y，Q C W，JIANG B.Research on tracking algorithms of coast phase space target in LEO constellation［J］.Electronic Measurement Technology，2009，32: 157-160.

［4］刘国海，施维，李康吉.插值改进EKF算法在组合导航中的应用［J］.仪器仪表学报，2007，28:1897-1901.LIU G H，SHI W，LI K J.Applacation of interpolationbased improved EKF algorithm in integrated navigation［J］.Chinese Journal of Science Instruction，2007，28: 1987-1901

［5］陈世华，潘鸿飞，朱璐.组合导航信息融合技术研究［J］.国外电子测量技术，2007，26:21-24.CHEN S H，PAN H F，ZHU L.Study on integrated navigation information fusion technology［J］.Foreign Electronic Measurement Technology，2007，26:21-24.

［6］张翔宇，王国宏，王娜，等.基于UKF的雷达和机载ESM扩维跟踪［J］.国外电子测量技术，2011，30:30-32.ZHANG X Y，WANG G H，WANG N，et al.Augmented tracking of radar and airborne ESM based on unscented Kalman filter［J］.Foreign Electronic Measurement Technology，2011，30:30-32.

［7］NATHAN B S，ROBERT A B，FRANK R C.Comparison of the extended and unscented Kalman filters for angles based relative navigation［C］//AIAA Astrodynamics Specialist Conference and Exhibit.Washington D.C.:AIAA，2008.

［8］付梦印，邓志红，闫莉萍.Kalman滤波理论及其在导航系统中的应用［M］.北京:科学出版社，2010:171-176.

Relative Navigation Algorithm for GEO Noncooperative Satellites Based on Line-of-Sight Measurement and Orbit Prediction

ZHANG Yang1，WANG Dianjun1，ZHU Zhibin2，GAO Enyu1
(1.Institute of Telecommunication Satellite，China Academy of Space Technology，Beijing 100094，China; 2.Beijing Institute of Control Engineering，Beijing 100190，China)

For noncooperative objectives，with limited measuring method，only angle measurement information can be achieved for the mid-long distance satellites.The line-of-sight-measurement relative navigation algorithm has low precision and observability for GEO satellites.Based on the combination of lineof-sight inter-satellite-measurement and orbit forecast information of ground-measurement，a method of relative navigation algorithm for GEO noncooperative satellites is presented.The system state equation based on the inter-satellite relative motion model is established.The measurement equation is established based on LOS and orbit forecast information.EKF(extended Kalman filter)and UKF(unscented Kalman filter)methods are adopted.The effects of orbit forecast information measurement accuracy and filtering methods on the navigation accuracy are illuminated via the simulation and analysis.

relative navigation;line-of-sight-measurement;extended Kalman filter;unscented Kalman filter

V448

A

1674-1579(2016)03-0021-06

10.3969/j.issn.1674-1579.2016.03.004

张 杨(1990—)，男，硕士研究生.研究方向为航天器动力学与控制;王典军(1968—)，男，研究员，研究方向为航天器控制;朱志斌(1981—)，男，高级工程师，研究方向为航天器控制;高恩宇(1983—)，男，高级工程师，研究方向为航天器总体设计.

*国家自然科学基金资助项目(61203196，11502017).

2016-02-07