倾斜轨道小卫星太阳高度角分析与机动方案设计*

丰保民，陈占胜，叶立军，季诚胜，朱 虹

(1.上海航天控制技术研究所，上海201109;2.上海市空间智能控制技术重点实验室，上海201109; 3.上海航天技术研究院，上海201109)

倾斜轨道小卫星太阳高度角分析与机动方案设计*

丰保民1，2，陈占胜3，叶立军1，2，季诚胜1，2，朱 虹1，2

(1.上海航天控制技术研究所，上海201109;2.上海市空间智能控制技术重点实验室，上海201109; 3.上海航天技术研究院，上海201109)

针对倾斜轨道小卫星必然会面对的光学姿态敏感器受阳光干扰的问题，分析太阳高度角的变化规律，提出了计算太阳高度角的经验公式，并在此基础上提出了平台偏航姿态机动方案，可以使光学姿态敏感器规避阳光干扰，并可以简化整星热控和帆板驱动设计，提高了整星的可靠性.

倾斜轨道;太阳高度角;姿态机动

0 引言

小卫星近十几年来已成为航天活动的主要领域.小卫星除了具有体积小、质量轻，研制发射运营成本低等特点外，还有两个突出特点:一是小卫星多为组网工作，组网机动灵活，二是应用广泛.现代小卫星应用已进入现代通信、航天、环境与资源、科学技术试验、飞行演示等众多领域.小卫星的上述两个特点决定了其轨道倾角的多样化.低轨倾斜轨道是小卫星经常采用的轨道.但是由于升交点赤经漂移和地球绕太阳公转运动，倾斜轨道上太阳光和轨道面夹角的变化要比太阳同步轨道复杂，对卫星的热控、太阳电池阵受晒以及星上光学姿态敏感器的布局影响很大.如果不进行针对性的设计，将严重影响卫星的可靠性和寿命.

倾斜轨道上太阳光照条件的变化主要由太阳高度角来衡量.太阳高度角即太阳矢量与卫星轨道面之间的夹角.已有多篇文献对太阳高度角进行了分析［1-2］，但主要是针对太阳同步轨道卫星进行的，并且太阳高度角计算表达式复杂，只能通过编程仿真给出太阳高度角的变化情况.对倾斜轨道卫星的研究多集中在热控和帆板驱动方面［3-5］，主要讨论倾斜轨道卫星受热和帆板受晒的问题，而对姿态控制方案则很少提及.目前对于倾斜轨道卫星控制系统，主要配置不怕光照的高精度数字太阳敏感器配合地球敏感器进行三轴定姿，控制方案与太阳同步轨道卫星基本相同.随着对小卫星平台精度指标要求的提高和高精度姿态敏感器成本的降低，倾斜轨道小卫星的控制系统将会配置高精度的光学姿态敏感器，那么就必须解决光学敏感器遇太阳照射的问题.

为有效规避倾斜轨道太阳光照的不利影响，采用星体偏航轴姿态调整是可行的解决思路.Kalweit［6］针对倾斜轨道卫星单自由度帆板对日定向问题提出了一种最优偏航角方法，其对应每一个太阳高度角的角度确定一个最优的偏航角θB，使星体偏航轴根据每轨太阳矢量符号分别偏置在±θE，再配合单轴驱动太阳帆板可以得到次优的光照条件.该方法虽然保证了帆板光照条件，但是由于倾斜轨道卫星的太阳高度角是连续变化的，因此Kalweit方法的最优偏航角实际也是连续变化的，在长期看仍然需要偏航轴存在角速度，这对观测载荷的工作是不利的.

为了规避太阳光对热控和光学敏感器布局的不利影响，本文首先根据低轨倾斜轨道卫星轨道面和平太阳的相对运动关系分析了太阳高度角的变化原因，给出了仅需输入轨道高度和轨道倾角即可描述太阳高度角变化规律的近似公式.在此基础上提出了适用于倾斜轨道卫星的星体偏航姿态机动+偏置的平台控制方案，可使星体按照太阳高度角的变化定期改变偏航轴姿态，有效规避光学敏感器遇太阳的问题，并降低了对整星热控和帆板驱动机构的要求.

1 太阳高度角经验公式

要解决倾斜轨道卫星的光学敏感器遇太阳问题，首先需要明确在给定的卫星轨道高度和轨道倾角的条件下太阳高度角的变化规律.本节给出仅需轨道高度和轨道倾角作为输入条件的太阳高度角计算经验公式.

1.1 太阳相对卫星的相对运动模型

假设太阳在黄道上匀速运动，并且忽略卫星由于轨道的大小而在轨道不同位置产生的太阳方向偏差.在地心赤道惯性坐标系中，定义 β为太阳高度角，表示太阳矢量与轨道平面间的角度.令 αs为太阳赤经，δs为太阳赤纬，Ω为升交点赤经，i为轨道倾角，则有

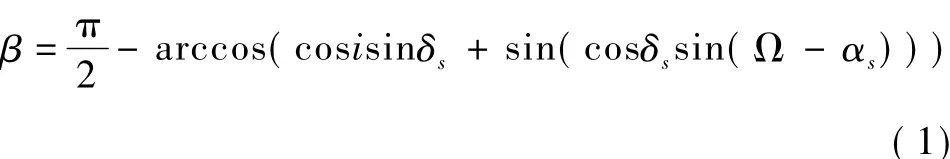
上式为依据轨道动力学建立的太阳高度角表达式，形式较复杂，太阳高度角与轨道倾角、黄赤交角之间关系的表达不够直观，不便于工程分析应用.本文将分析太阳高度角的变化原因，利用简单的三角函数对太阳高度角计算公式进行拟合，给出一个简便的经验公式，显式地表示出太阳高度角与黄赤交角、卫星轨道倾角和升交点赤经摄动速度(与轨道高度关联)等因素与之间的关系.

1.2 太阳高度角经验公式

令平太阳运动速率为ω0，有

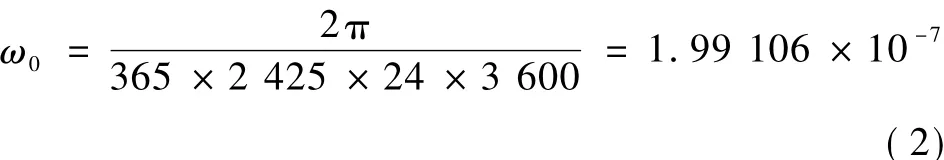
量纲为rad/s.地球扁率摄动使卫星轨道面在空间进动，平均进动速率等于卫星升交点赤经的平均漂移速率ωsat［7］.对于圆轨道小卫星，有

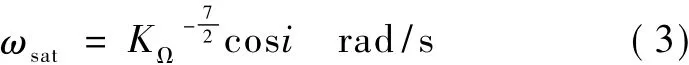
其中，KΩ=1.5J2R2e为带谐项系数，Re为地球半径，μ为地心引力常数，a=Re+Ho为倾斜轨道小卫星轨道半长轴，Ho为轨道高度，i为轨道倾角.

由(3)式可知，当轨道高度 Ho和轨道倾角 i确定后，升交点赤经在赤道上的运动可看作是匀速运动.对于轨道倾角在0°～90°之间的倾斜轨道小卫星，升交点赤经向西漂移，即卫星升交点自东向西匀速运动.在地心惯性坐标系XY平面上定义卫星升交点矢量Vomg由地心指向卫星升交点，Vomg绕Z轴顺时针转动.定义平太阳矢量Vsun由地心指向平太阳，则Vsun绕Z轴逆时针转动，如图1所示.

随着太阳和卫星轨道面的运动，矢量 Vsun与矢量Vomg之间夹角时刻变化.该夹角表征了太阳与卫星轨道面夹角，即太阳高度角的变化.由于 Vomg和Vsun两者运动方向和角速率均不同，矢量 Vomg和矢量Vsun必然会多次相遇(两个矢量重合定义为相遇)，表明太阳高度角变化具有周期性.两次相遇之间的时间即为太阳高度角变化周期.由于两者运动为圆周且运动方向相反，因此周期长度由两矢量的角速率之和决定.

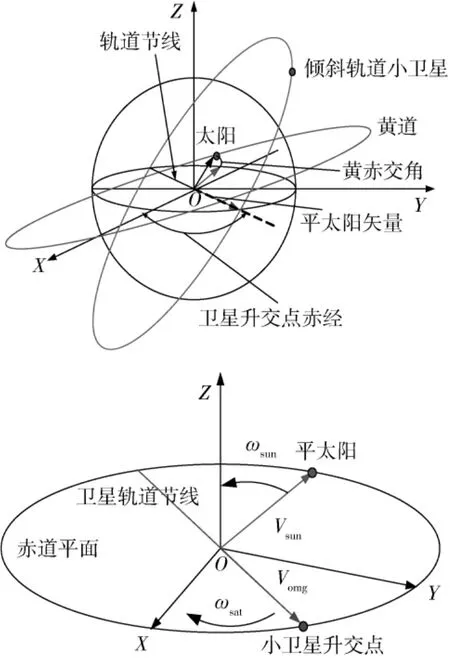
图1 倾斜轨道卫星与太阳的相对运动关系Fig.1 Relative motion relationship between the sun and inclined-orbit satellite

由图 1可知，当 Vomg和 Vsun夹角为±2，±4，…)时，Vomg与Vsun平行，太阳高度角相应地等于零;当矢量 Vomg和矢量 Vsun夹角等于±1，±3，±5，…)时，矢量 Vomg和矢量 Vsun垂直，此时太阳高度角达到极大值.由于黄赤交角的存在，太阳高度角的最大值将由轨道倾角和黄赤交角以及具体时刻的相位共同决定.

根据前面的分析可知，太阳高度角的变化可分解为快变和慢变两部分.快变部分的周期由卫星轨道和平太阳的相对运动速度决定，周期 Ti=，幅值与轨道倾角幅值相关;慢变部分的周期主要由平太阳运动决定，约为1年，幅值与黄赤交角相关.综上，可以使用余弦函数和的形式显示地给出影响太阳高度角变化规律主要因素之间的关系，得到描述太阳高度角变化规律的公式可简化为:

其中，ε=23.45°为黄赤交角，w0为平太阳角速率，wsat为卫星升交点赤经漂移速率，φb，φc为初始相位，在实际应用中可以选择两个具体时刻的真实太阳高度角计算得到.

算例.以轨道倾角i=35°，轨道高度Ho=300 km的倾斜圆轨道小卫星为例，仿真时间为13 000 h(约1.5 a)，按照经验公式(4)得出太阳高度角的长期变化规律如图2所示，近似偏差变化情况如图3所示.由图2～3可知，经验公式得到的太阳高度角的变化周期和幅值变化与真实太阳高度角相符.由于经验公式仅考虑了升交点赤经的摄动因素，忽略了其他参数摄动，因此计算的太阳高度角近似值与真实值之间存在偏差，但不随时间发散，对太阳高度角变化规律的工程分析无影响.

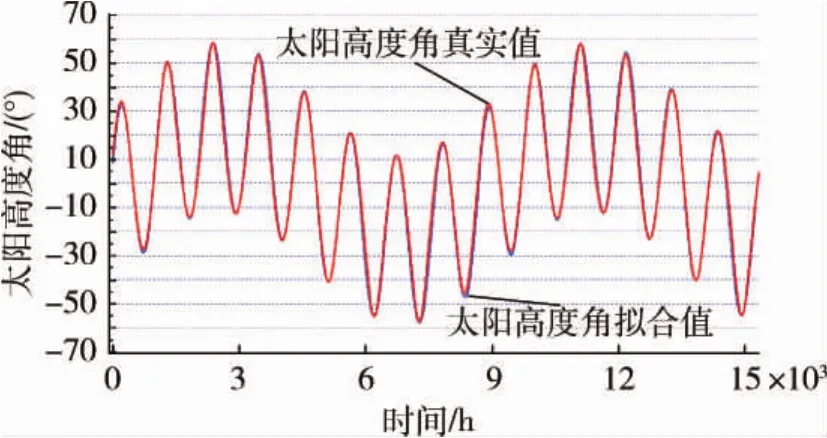
图2 i=35°，Ho=300 km的太阳高度角Fig.2 Solar height angle of satellite with i=35°and Ho=300 km

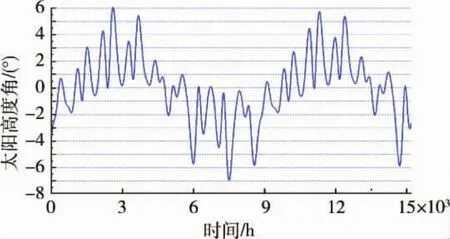
图3 太阳高度角拟合偏差Fig.3 Fit error of solar height angle

2 规避光照的倾斜轨道小卫星姿态机动方案设计

2.1 光照对姿控敏感器的影响

根据前面对倾斜轨道小卫星太阳高度角的分析可知，太阳高度角的长期变化具有如下规律:1)太阳高度角变化是周期性的，变化周期与平太阳速率和卫星升交点进动速率有关;2)太阳高度角从负极大值连续地变化到正极大值，即太阳光连续地交替照射卫星的左侧和右侧;3)太阳高度角幅值变化范围的上限值由轨道倾角和黄赤交角共同确定.

因此倾斜轨道上卫星不存在固定的背阳面，对光学姿态敏感器不论如何布局都会被阳光照射到.当太阳光进入到敏感器视场时，敏感器将不能正常工作.若阳光频繁地进入光学敏感器视场，将对敏感器的镜头造成损伤，降低卫星平台的可靠性和寿命.

2.2 平台姿态机动方案

为规避倾斜轨道上太阳光的不利影响，卫星姿控系统可采取星体偏航轴姿态定期调整的方案.将卫星偏航轴姿态随太阳位置的变化进行对应的调整，可以在卫星局部创造出有利的光照环境，并可以形成固定的散热面，简化热控系统设计.

根据式(4)可知，太阳高度角的变化范围可表示为［－βm，βm］，βm(＞0)为 β角变化周期内的极值.由于角连续变化，可将β角的变化范围分为若干个相邻的区间，每个区间内对应一个固定的偏航轴偏置角.控制系统在β角经过临界阈值时进行一次偏航姿态机动，使星体偏航轴固定在新的偏置角上.为工程实际考虑，偏航轴偏置角不宜设置过多，可选择偏置偏航姿态角为kπ/2(k=0，±1，2).

由于星体偏航姿态在不同的太阳高度角区间内可偏置在固定角度，相当于增加了一维运动自由度，在此条件下可以采用单自由度帆板驱动机构.若小卫星使用一维驱动机构的太阳电池阵，星体偏航机动阈值的选择除了要考虑星上光学敏感器布局并应对热控设计有利之外，还要考虑太阳电池阵的受晒情况.对于沿星体俯仰轴正装的一维驱动太阳帆板，太阳高度角的变化直接体现在太阳矢量与帆板法线夹角的变化.当太阳高度角较小情况下，帆板受晒情况与太阳同步轨道卫星相同，星体偏航轴姿态可保持0°偏置;随着太阳高度角幅值的增大，帆板受晒情况有所恶化，星体偏航轴姿态应有所调整以适应光照条件.实际应用中，偏航机动阈值的选择与卫星具体的太阳电池阵的充电能力、整星功耗等具体约束有关，因而设计时取值会有所不同，下文令阈值为βY(βY＞0).

根据上述分析，偏航机动方案设计可分以下两种需求讨论，分别如图4、图5所示(Xb、Yb为小卫星本体坐标系X、Y轴，Xo、Yo为卫星轨道坐标系X、Y轴).

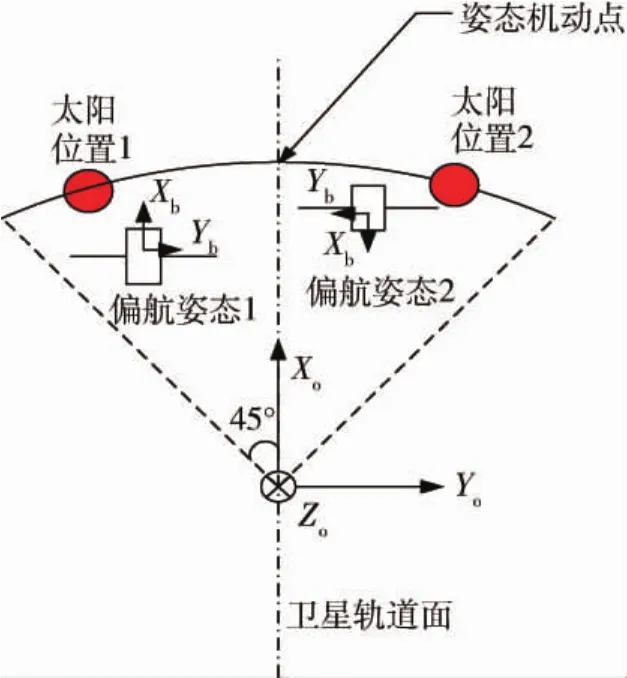
图4 适用于需求1的偏航机动方案Fig.4 Yaw-axis maneuver scheme for requirement 1

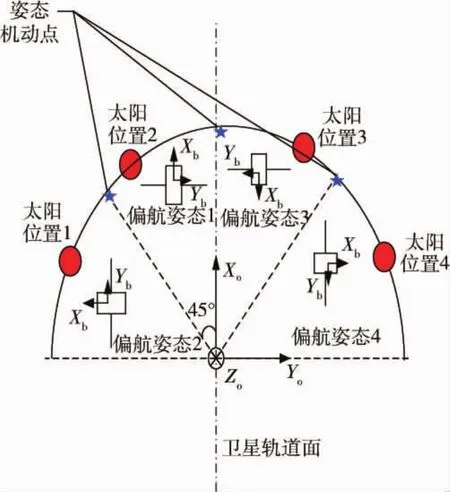
图5 适用于需求2的偏航机动方案Fig.5 Yaw-axis attitude maneuver scheme for requitement 2

第一种需求仅考虑光学敏感器规避受照，可将角变化范围分为［0°，βm］和［－βm，0°］两个区间，则星体偏航姿态角ψ的偏置规则为:

1)当β∈［0°，βm］时，ψ=0°;

2)当β∈［－βm，0°］时，ψ=180°.

第二种需求在光学敏感器规避受照基础上还考虑星体Y轴一维驱动机构帆板良好受晒.当βm＞βY时，可将 β角分为［0°，βY］、［βY，βm］、［－βY，0°］和［－βm，－βY］共4个区间，则星体偏航姿态的偏置规则为:

1)当β∈［0°，βY］时，ψ=0°;

2)当β∈［βY，βm］时，ψ=－90°;

3)当β∈［－βY，0°］时，ψ=180°;

4)当β∈［－βm，－βY］时，ψ=90°.

现以第二种需求为例对方案有效性进行仿真分析.假设某小卫星运行轨道的倾角i=50°，轨道高度Ho=400 km，在卫星 +Yb侧安装一台星敏感器，光轴方向朝向+Yb且向－Zb方向上翘20°，小卫星在Yb轴两侧各安装由一维机构驱动的太阳电池阵.

若不采用偏航机动方案，星体始终保持偏航0°的飞行姿态，星敏视轴与太阳矢量夹角变化情况如图6所示.由图6可知，随着太阳高度角幅值的增大，星敏视轴与太阳矢量夹角逐渐变小到0°，即太阳光逐渐进入星敏视场直至照射到星敏镜头.这不仅会干扰星敏正常工作，而且会损伤星敏感器.

若采用本文提出的偏航机动方案，星敏视轴与太阳矢量夹角的变化以及对应的卫星偏航轴姿态角的关系如图7所示.可知，按照本文提出的偏航机动规则，通过星体偏航姿态随太阳高度角进行对应的调整，星敏视轴与太阳矢量的夹角始终保持大于40°，可有效规避星敏感器遇太阳无法工作的情况.

图6 星体偏航轴0°偏置时星敏遇太阳情况Fig.6 Star sensor when meeting the sun with 0°yaw attitude bias

图7 偏航机动后星敏遇太阳情况Fig.7 Star sensor avoiding the sunlight by yaw axis attitude maneuver

3 结论

本文提出了用于分析计算倾斜轨道小卫星太阳高度角的经验公式，并在此基础上针对光学姿态敏感器规避太阳光的问题，提出了平台偏航姿态机动方案.该方案使卫星获得了相对固定的背阳面，为光学姿态敏感器的布局、整星热控和帆板驱动机构选型带来了便利，可提高整星的可靠性.

［1］肖业伦.航天器轨道设计中太阳照射条件的分析［J］.航天器工程，1998，7(2):10-16.

［2］王永谦.太阳同步轨道的太阳相对于轨道面入射角的计算方法［J］.航天器工程，1995，4(4):65-73.

［3］徐向华，任建勋，梁新刚.近地倾斜轨道航天器在轨热辐射分析［J］.太阳能学报，2004，25(5):717-721.XU X H，REN J X，LIANG X G.Thermal radiation analysis of spacecraft on inclined near earth orbit［J］.Acta Energiae Solaris Sinica.2004，25(5):717-721.

［4］王颖，顾荃莹.倾斜轨道航天器太阳翼对日跟踪方法探讨［J］.航天器工程，2009，18(3):36-40.WANG Y，GU Q Y.Methods of solar array tracking for inclined-orbitsatellite［J］. SpacecraftEnineering，2009，18(3):36-40.

［5］林竹翀.航天器太阳帆板对日定向方法研究［D］.长沙:国防科学技术大学，2010.LIN Z C.Study on spacecraft solar panel sun-tracking method［D］.Changsha:National University of Defense Technology，2010.

［6］KALWEIT C C.Optimum yaw motion for satellites with a nadir-pointing payload［J］.Journal of Guidance，1983，6(1):47-52.

［7］章仁为.卫星轨道姿态动力学与控制［M］.北京航空航天大学出版社.1998.

Solar Height Angle Analysis and Attitude Maneuver Design of Inclined-Orbit Small Satellite

FENG Baomin1，2，CHEN Zhansheng3，YE Lijun1，2，JI Chengsheng1，2，ZHU Hong1，2
(1.Shanghai Institute of Spaceflight Control Technology，Shanghai 201109; 2.Shanghai Key Laboratory of Aerospace Intelligent Control Technology，Shanghai 201109; 3.Shanghai Academy of Spaceflight Technology，Shanghai 201109)

Considering the optic attitude sensor of inclined-orbit small satellite interfered by sunlight，the variation law of solar height angle is analyzed.For computing and analyzing easily，a handy experience formula of solar height angle is proposed.Based on the formula，a yaw-axis attitude maneuver scheme is presented，which can avoid sunlight interferer and make thermal control design and solar array drive law design conveniently.

inclined-orbit;solar height angle;attitude maneuver

V448

A

1674-1579(2016)03-0033-05

10.3969/j.issn.1674-1579.2016.03.006

丰保民(1976—)，男，高级工程师，研究方向为卫星控制系统设计;陈占胜(1970—)，男，研究员，研究方向为卫星总体设计;叶立军(1982—)，男，工程师，研究方向为卫星控制系统设计;季诚胜(1981—)，男，高级工程师，研究方向为卫星控制系统设计;朱 虹(1972—)，女，研究员，研究方向为卫星控制系统设计.

核攀资助项目(ZY2015-003-3).

2016-02-17