过度离散型数据的统计模拟与分析

李荣　陈莉　王平鲜

摘 要 针对车险索赔次数数据经常出现的过度离散问题，采用数值模拟的方法，分别使用泊松模型（Poisson）、负二项回归模型（NB）以及广义泊松模型（GP）对不同程度的过度离散车险索赔次数数据进行拟合，并用均方误差、偏差以及AIC和BIC准则对Poisson、NB、GP三种模型的优良性进行比较分析，得到了不同条件下三种模型的优良性，并针对不同的条件给出了模型选择的建议.

关键词 过度离散；车险索赔次数数据；负二项模型；广义泊松模型

中图分类号 O212.1 文献标识码 A

1 引 言

保险公司在进行费率厘定时，需要建立索赔次数模型与索赔强度模型，在实际应用中，车险索赔次数数据常常出现过度离散现象，亦即观察值方差大于均值的情况.刻画车险索赔次数数据最常用的是泊松模型，但当数据存在过度离散现象时，泊松模型不再适用，这时可以用负二项模型或者广义泊松模型替代泊松模型，结果能从一定程度上改善过度离散问题，但不是所有的情况都适用.杨肇和朱凯旋针（2003）、郭海强等（2005）对logistic回归中的过度离散现象，通过调整协方差以及用估计的离散参数影响参数估计和参数的标准误来调整回归系数的假设检验结果，结论得到一定的改善[1-，2]；Noriszura Tsmail和Abdul Aziz Jemain（2007）用负二项模型与广义泊松模型作了实证研究，他们对一组特定的理赔次数找到了合适的模型[3]；同年，Richard Berk和John MacDonald对泊松模型和负二项模型进行了讨论，得出，在犯罪学应用中用负二项模型去替代泊松模型不是任何情况都适用[4]；之后的一些文献讨论了过度离散现象的检验，也将过度离散模型运用到了不同的领域，杨娟（2013）等基于一组真实的B2C商务数据，比较了泊松模型、负二项模型、Tweedie模型对此数据的拟合效果、预测效果以及对过度离散的刻画[5]；可见，过度离散现象在理赔次数中是普遍存在的，因此，为数据寻求合适的模型是必要的.

本文将考虑在不同过度离散程度条件下，基于均方误差准则、偏差准则、AIC准则与BIC准则，对Poisson，NB，GP三种模型的优良性进行比较研究，为过度离散数据寻求合适的模型.

2 基本模型

2.1 泊松回归模型

对计数数据进行分析通常采用的最基本的模型是泊松模型，设随机变量Y服从Poisson分布，记为Y～Poisson（μ），则概率密度函数为：

3.3 结果分析

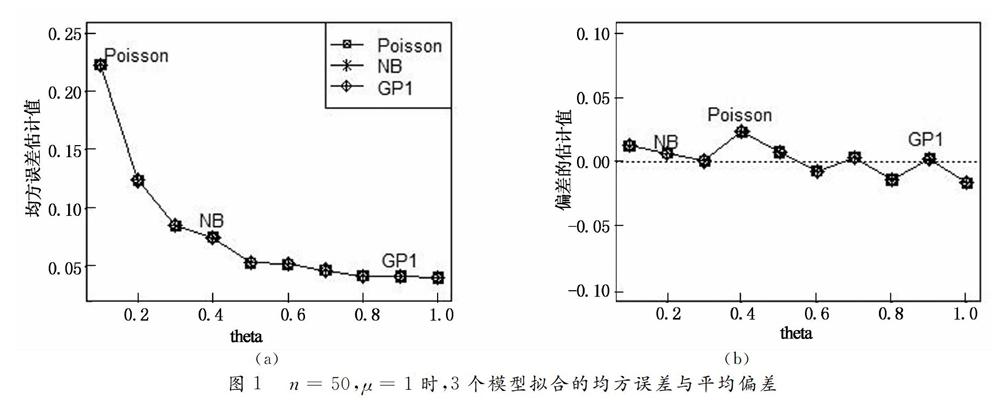
首先，在均方误差与偏差准则下对3个模型进行比较研究，如图1所示，当n=50，μ=1时，Poisson模型、NB模型、GP1模型的均方误差都随着离散程度的增大逐渐减小，且3个模型的均方误差完全相等，其值都非常小；偏差在零的附近波动，且3个模型的偏差完全相等，其值接近于零，可以得出，3个模型对于参数估计，效果都很好，实际应用时，择一即可.随着样本量n以及均值μ的增大，亦即n=50，μ=2、n=100，μ=1、n=100，μ=2的情况，结论与n=50，μ=1时类似，说明3个模型在参数估计上差别不显著，如果只是针对参数估计，那么3个模型择一即可.而就Poisson模型来讲，针对过度离散车险索赔次数数据，虽然其参数估计值与NB模型、GP1模型差别不明显，但它会低估参数的标准误与增大参数的显著性水平，所以在数据存在过度离散现象时，Poisson模型要慎用[5].

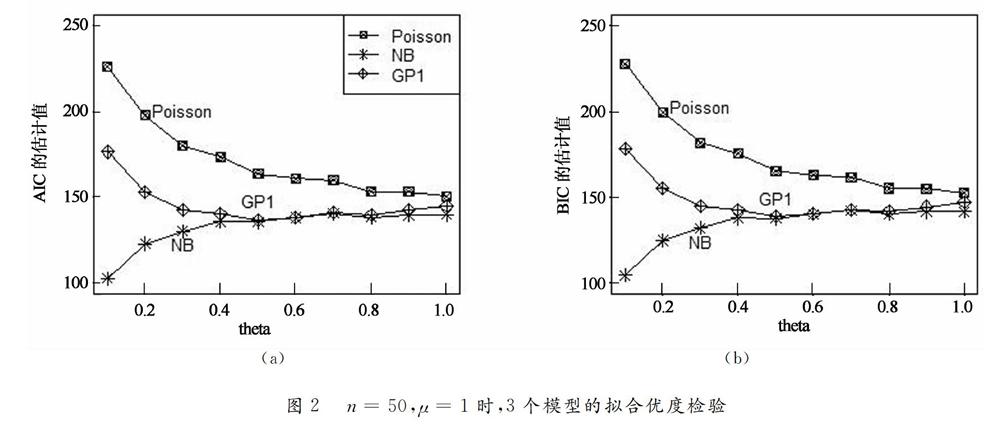
其次，对3个模型进行拟合优度检验，如图2所示，当n=50，μ=1时，Poisson模型、GP1模型的AIC值逐渐减小且随着离散程度的增大趋于平稳，NB模型的AIC值逐渐增大且随着离散程度的增大也逐渐趋于平稳；GP1、NB模型整体优于Poisson模型；当θ<0.5时，NB模型优于GP1模型，当0.5<θ<0.8时，NB模型与GP1模型几乎无差别，当θ>0.8时，NB模型优于GP1模型.样本量n=50不变，均值增大到μ=2时，结论如图3所示，可以看出，模型AIC值变化趋势和μ=1时一致，说明数据均值变化对模型的优良性没有影响，同样，当n=100，μ=1、n=100，μ=2的情况，结论也类似，说明样本量n的变化对模型的优良性也没有影响.对于BIC值，其变化趋势与AIC值大致相同，这里不再赘述.

4 结 论

本文应用Monte Carlo模拟方法比较研究了Poisson模型、NB模型、GP1模型对于不同离散程度的车险索赔次数数据的拟合效果，并且对3个模型的优良性进行了比较研究.得出以下结论：1）从模型参数估计值来看，Poisson模型、NB模型、GP1模型3个模型之间没有显著的区别，如果只是参数估计，三者择一即可，但当数据存在过度离散现象时，用Poisson模型去拟合过度离散数据会低估参数的标准误与增大参数的显著性水平，出现较大的模型偏差，所以Poisson要慎用；2）由模型拟合优度检验来看，NB模型与GP1模型整体优于Poisson模型，当θ<0.5时，NB模型优于GP1模型，此时选择NB模型较好；当0.5<θ<0.8时，NB模型与GP1模型几乎无差别，二者择一即可；当θ>0.8时，NB模型优于GP1模型，此时选择NB模型较好；并且模型选择与样本量n、均值μ的大小无关.

参考文献

[1] 杨肇，朱凯旋.Logistic回归分析中的过度离散现象及纠正[J].中国卫生统计，2003（4）：48-49.

[2] 郭海强， 程大丽，黄德生，等.Logistic回归中数据过度离散及其软件处理[J].中国医科大学学报，2005（2）：144-145+166.

[3] Noriszura ISMAIL， Abdul Aziz JEMAIN. Handing overdispersion with negative binomial and generalized poission regression models[C]//Proceedings of Casualty Actuarial Society Forum，2007：102-158.

[4] Richard BERK， John M.MACDONALD. Overdispersion and Poisson regression [J]. Journal of Quantitative Criminology， 2008，24 （3）：269-284.

[5] 杨娟，谢远涛.基于过度离散广义线性模型的来电量预测[J].统计与决策， 2013（6）：33-36.

[6] Jiewu HUANG， Hu YANG. A twoparameter estimator in the negative binomial regression model[J]. Journal of Statistical Computation and Simulation， 2014，84（1）：124-134.