基于人工神经网络和随机游走模型的汇率预测

洪嘉灏　李雄英　王斌会

摘 要 由于金融数据具有随机性特征，使得建模和预测变得极其困难.提出一种组合预测方法，即假定任何金融时序数据由线性和非线性两部分组成，将其中线性部分的数据通过随机游走（RW）模型进行模拟，剩余的非线性残差部分由前馈神经网络（FANN）和诶尔曼神经网络（EANN）协同处理.从实证结果可知，该组合方法相比单独使用RW、FANN或EANN模型有更高的预测精度.

关键词 诶尔曼神经网络；人工神经网络；随机游走模型；组合预测；金融时间序列

中图分类号 F224 文献标识码 A

1 引 言

金融时间序列与经济环境及商业环境有关，如股市，汇率，物价指数，国民收入和净出口等.选择一个合适的金融数据模型，需要正确地识别金融市场与整体经济之间的内在关系[1].在实践中非常困难.因为一个金融时序数据的动态变化受到多个经济变量的影响，包括经济增长，利率，通货膨胀，通货紧缩，政治决策和心理因素等多个复杂的经济变量[1].

这些年来，关于金融时间序列的分布特征、模型模拟及预测等已经有了大量的研究工作[2，3].线性统计模型，如指数平滑法[4]和ARIMA[5]模型等，已经大量应用于金融数据的预测.ARIMA模型的一个分支，即随机游走模型（Random Walk model）[1，6]，已经成为这个领域的主流统计技术.在一个简单的随机游走模型中，每一期的预测值被认为是最近一期的观测值和随机误差项的总和.目前，简单随机游走模型是金融时间序列分析中最主要的线性模型（尤其是汇率数据）[7].对随机游走模型的改进，如带漂移项的随机游走模型和误差修正，也有了很多相关的研究[1].尽管随机游走模型具有简单性和显著的预测精度，但是其主要缺点是内在的线性形式.随机游走模型未能捕获存在于金融时间序列中的非线性特征[2，7].非线性是金融时间序列的缺省特征，因此，通过一个随机游走模型近似它是不充分的.在这种情况下，人工神经网络是一种不错的选择.由于其非线性，非参数，自适应和噪声耐受性，人工神经网络在金融时间序列预测领域获得了广泛的关注[2，3].这些显著的特征使得人工神经网络模型能够有效地识别解释变量之间导致金融时序图产生不规则波峰和波谷的内在机理.与其他非线性统计模型不同的是，人工神经网络能够在不了解底层数据计算过程的情况下进行非线性模拟[8].不少研究者对比了人工神经网络和随机游走模型预测金融数据时的表现，也研究出了许多有益的结果：如Dunis and William发现神经网络相对于一般的统计模型可以提供更高的预测精度；Sun[1]发现在预测汇率时，人工神经网络表现出比随机游走模型更差的预测精度等等.但是，对于预测金融数据，一个金融时间序列一般包含了线性部分和非线性部分，单独使用人工神经网络模型或随机游走模型并不合适.上述研究无法确定人工神经网络模型和随机游走模型中哪一个更适应于预测这类金融数据.从而激励着去寻找一种组合机制去预测汇率.对于金融数据模型的预测，zhang[7]首次将随机游走模型和神经网络模型结合起来，国内学者熊志斌也做了ARIMA融合神经网络的人民币汇率预测模型研究[9].

本文假设任何金融时间序列由线性部分和非线性自相关部分组成，且可以从时间序列中剥离、单独建模.将随机游走模型和神经网络模型结合起来对金融数据进行预测.主要步骤如下：首先，随机游走模型用于拟合金融时间序列的线性部分，由观察值和随机游走模型拟合值之间的差计算样本内残差.根据假设，这些残差只包含非线性关系；第二，FANN和EANN将用于分别拟合这些残差值，并由2个模型产生的预测值的平均值得到想要的残差估计；第三步，由随机游走模型预测时间序列的线性部分；最后，将线性部分和非线性部分所得到的预测值加总，获得期望的最终预测.

2 随机游走模型

随机游走模型是金融时序分析最流行和有效的统计模型，也被广大的研究生所研究和使用，这个模型假设最近的观察值是对下一期预测值的最佳指南.在数学上，一个简单的RW模型被表示如下：

其中，和yt是时间序列中的观察值，εt是一个白噪声并且εt～N（0，σ2）.

从式（1）中可以看出，一个随机游走模型表明所有与未来相关的信息已经包含在可用的数据里，这个模型因为被使用较多，所以非常容易理解和实现.根据有效市场的假说，随机游走模型是外汇汇率预测中最主要的线性模型，而且大量研究指出许多基于线性结构的预测技术并没有比简单的随机游走模型更有效.

一个随机游走模型的成功很大程度上取决于随机误差项，按照定义，随机误差项是独立同分布的.在本文中将生成独立同分布的伪随机正态变量εt～N（0，σ2），其中σ2是样本内数据集的方差.

3 人工神经网络（ANN）模型

3.1 前馈神经网络 （FANN）

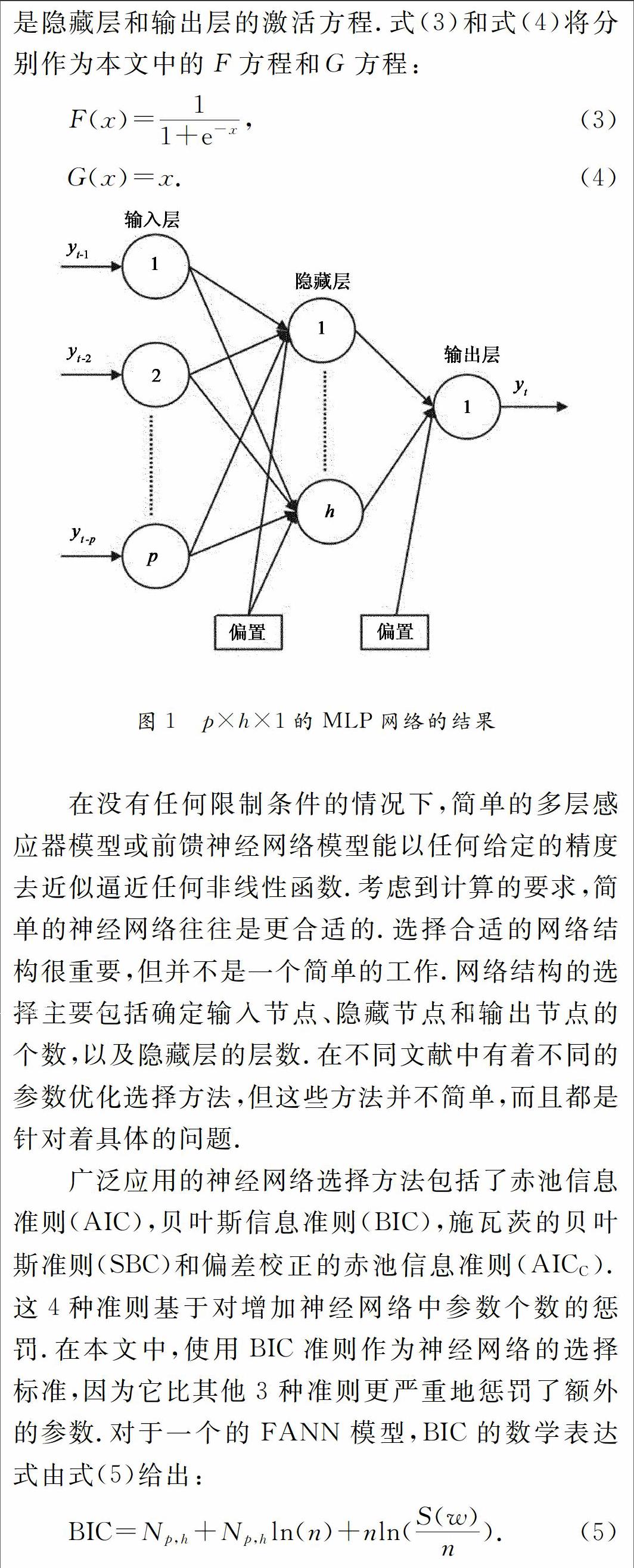
在所有可用的仿生预测方法中，人工神经网络无疑是最流行且最成功的.人工神经网络最初起源于对人脑结构的模仿，渐渐地，神经网络技术在众多领域起到了极为重要的作用，如分类、识别和预测.人工神经网络通过若干互相连接的分布在不同层的神经元来学习数据的内在关系.多层感知器（MLP）是最被认可的人工神经网络的结构，用于时间序列预测问题.一个MLP基本上是一个输入层，一个或多个隐藏层和一个输出层的前馈结构.在每层中有许多个处理结点，其通过不可逆的链接连接到下一层.单层次的隐藏节点已经足以解决许多最实际的问题.图1描述了一个典型的MLP结构（p个输入结点，h个隐藏结点和一个输出结点）.

在没有任何限制条件的情况下，简单的多层感应器模型或前馈神经网络模型能以任何给定的精度去近似逼近任何非线性函数.考虑到计算的要求，简单的神经网络往往是更合适的.选择合适的网络结构很重要，但并不是一个简单的工作.网络结构的选择主要包括确定输入节点、隐藏节点和输出节点的个数，以及隐藏层的层数.在不同文献中有着不同的参数优化选择方法，但这些方法并不简单，而且都是针对着具体的问题.endprint

广泛应用的神经网络选择方法包括了赤池信息准则（AIC），贝叶斯信息准则（BIC），施瓦茨的贝叶斯准则（SBC）和偏差校正的赤池信息准则（AICC-）.这4种准则基于对增加神经网络中参数个数的惩罚.在本文中，使用BIC准则作为神经网络的选择标准，因为它比其他3种准则更严重地惩罚了额外的参数.对于一个的FANN模型，BIC的数学表达式由式（5）给出：

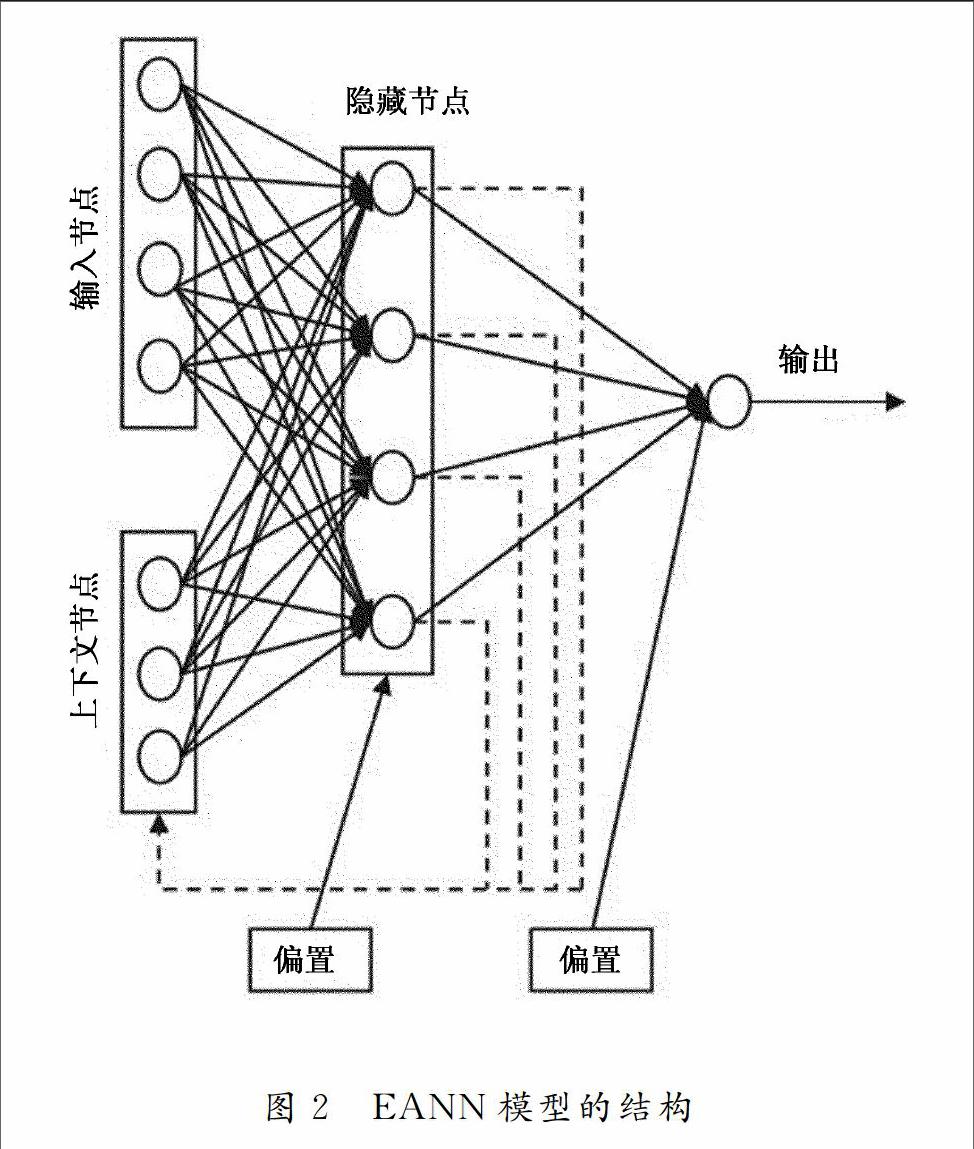
3.2 诶尔曼人工神经网络（EANN）

类似于常见的前馈型神经网络（FANNs），时间递归神经网络在金融时间序列预测领域也相当流行.诶尔曼人工神经网络是一种简单的时间递归神经网络，除了3种常见的层次，还有额外的上下文层和反馈连接.在每一个计算步骤中，隐藏层的输出被再次反馈到上下文层，如图2所示.这种递归使得神经网络动态化，从而能够实现对处理结点非线性时间依赖的映射.EANN模型通常比相同结构的FANN提供了更好的预测性能.然而，EANNs比FANNs需要更多数量的网络连接和记忆单元.

使用相同的网络结构的FANN和EANN模型，不同之处在于EANN模型隐藏层的神经元是对应FANN模型中神经元的5倍.

4 组合方法的建模

在本文中，决定同时利用随机网络模型和神经网路模型来预测金融数据.虽然这些模型有着广泛的应用，但是他们之中没有一个模型能够在所有预测情况之下都最好.例如，RW模型不适合于识别非线性模式，类似地，使用人工神经网络处理线性问题时产生的结果也好坏参半.因此，更科学的做法是找一种组合方法去结合这两种模型的长处，而不是单独地去应用它们.假设，一个金融时间序列由从线性和非线性两部分构成，能从时间序列中分离出来并单独地建模.从数学上讲：

这种组合方法的显著特点如下：①任何金融时间序列都由线性部分和非线性部分组成，通过随机游走模型拟合线性部分，神经网络模型拟合非线性残差部分，提高了总体的预测精度；②类似的组合方法最早由Zhang推出，在他们的方法中，时间序列的线性部分由ARIMA模型来拟合而剩余的非线性残差部分由FANN来拟合.然而，该组合方法同时结合了FANN模型和EANN模型两种模型的优势，能更好地识别非线性自回归结构；③这种组合机制是基于一种简单而有效的想法，相当容易实施和解释.④值得注意的是，如果金融时间序列中的线性和非线性部分存在着适当比例的自相关结构，那所提出的组合方法将能显着改善预测精度.如果这2个部分自相关程度较弱，那该方法可能并不合适.

5 实验结果与讨论

为了验证所提出的组合方法的有效性，本文用到了三组数据：①港币兑换美元汇率，包括了从1994年8月到2015年6月港币兑换人民币的每月汇率；②美元兑换人民币汇率，包含从2005年5月到2015年6月美元兑换人民币的每月汇率；③人民币兑换港币汇率，包括了从1995年1月到2015年6月人民币兑换港币的每月汇率.（数据来源：汇率数据取自国泰安数据库）（见表1）

从图3中可以清楚地看到3个时间序列中不规则非平稳的变化.

图4和5中，画出了3种时间序列的实际曲线和通过组合模型所描绘的预测值曲线.在每个图中，实线和虚线分别表示实际和预测序列.港币美元汇率与人民币港币汇率数据的预测误差较小，预测值与原始值的走势趋于一致.预测人民币港币汇率的预测效果没有港币美元汇率与人民币港币汇率好，预测值的总体走势与原始值一致.三组汇率数据的原始值和他们的预测值之间的接近程度是显而易见的.

6 总 结

众所周知，设计一个合适的模型来预测金融数据是时间序列研究领域的一个重大挑战，也是极其不易之事.这主要是因为金融时间序列中的不规则运动及突然的转折点使得实际中很难去理解和预测.基于金融数据独特的随机性特征，本文构建了人工神经网络和随机游走模型对中国的汇率数据进行预测.

本文构建的新模型结合了随机游走模型，FANN模型和EANN模型3种模型的优势去预测金融数据.并且从实证结果表明，预测值与原始值的走势趋于一致，港币与人民币之间的预测误差不大，但是对于相对于人民币汇率的预测，美元汇率的预测效果更好.从预测误差看，均比每个单独的模型效果要好.从三组真实的金融时间序列的实证结果清楚地表明，本文新构建的组合方法极大地提高了整体的预测精度.因此，我们的新模型在汇率预测方面上有更高的准确性和适用性.

参考文献

[1] Y SUN. Exchange rate forecasting with an artificial neural network model： can we beat a random walk model？ [D] New Zealand：Christchurch，Lincoln University， 2005.

[2] A HUSSAIN， A KNOWLES， P LISBOA，et al. Financial time series prediction using polynomial pipelined neural networks[J]. Expert Systems with Applications， 2008， 35（3）： 1186-1199.

[3] M SEWELL. The application of intelligent systems to financial time series analysis[D].London：Department of Computer Science， UCL，2010.

[4] C LEMKE，B GABRYS. Metalearning for time series forecasting and forecast combination[J]. Neurocomputing， 2010， 73（10）： 2006-2016.

[5] G BOX， G JENKINS， G REINSEL. Time series analysis： forecasting and control[M].London John Wiley & Sons， 2011. 734

[6] E TYREE， J LONG. Forecasting currency exchange rates： neural networks and the random walk model[J]. Citeseer， 1995（1）：981-996.

[7] G ZHANG. Time series forecasting using a hybrid ARIMA and neural network model[J]. Neurocomputing， 2003， 50： 159-175.

[8] G ZHANG. A neural network ensemble method with jittered training data for time series forecasting[J]. Information Sciences， 2007， 177（23）： 5329-5346.

[9] 熊志斌.ARIMA融合神经网络的人民币汇率预测模型研究[J].数量经济技术经济研究： 2011（6）：64-76.endprint