基于改进萤火虫算法的二维Otsu图像分割法

周晨航, 田力威, 赵宏伟

(1. 沈阳大学 信息工程学院, 辽宁 沈阳　110044;

2. 辽宁省物联网信息集成技术工程研究中心, 辽宁 沈阳　110044)



基于改进萤火虫算法的二维Otsu图像分割法

周晨航1, 田力威2, 赵宏伟2

(1. 沈阳大学 信息工程学院, 辽宁 沈阳110044;

2. 辽宁省物联网信息集成技术工程研究中心, 辽宁 沈阳110044)

摘要:对二维最大类间方差(2-D Otsu)算法和萤火虫算法研究现状进行了调查研究.为了解决二维Otsu图像阈值分割方法存在的计算复杂度高、实时性差等缺点,提出了一种将改进的萤火虫算法与二维Otsu算法结合的图像分割算法,即通过自适应惯性权重优化的萤火虫算法(IFA)搜寻图像分割的最佳阈值.实验结果表明,改进后的算法能够很好的实现图像分割的效果,有效地缩短了图像分割的运行时间,可以运用于图像分割的实时处理.

关键词:最佳阈值; 二维Otsu; 惯性权重; 萤火虫算法; 图像分割

图像分割是数字图像处理技术中的一种重要方法,它简化了图像并且改变图像的表现形式,从而使图像更容易被理解和分析.图像分割的精确度对后续任务的处理会起到直接的影响,因此对其进行研究具有重要的理论价值和实际意义[1-2]. 常用的图像分割方法有:基于阈值的分割方法[3]、基于区域的分割方法[4]、基于边缘的分割方法[5]以及基于特定理论的分割方法等.其中,基于阈值的分割方法简单、有效、稳定,是实际应用过程中常用的一种图像分割技术.

在阈值分割技术当中,最大类间方差法[6-7](Otsu算法)是最常用的分割方法之一,但是一维Otsu算法没有考虑到周围像素点对中心像素点的影响,不能很好地处理图像中的噪声,因此,刘建庄[8]等人提出了二维Otsu算法,较一维Otsu算法在图像分割效果上取得了很大的改善. 但仍存在耗时多、图像分割精度低、图像误分割等问题.范九伦[9]等人在二维Otsu算法的基础上提出了曲线阈值型Otsu算法, 吴一全[10]等人提出了一种新的二维直方图区域斜分方法并进行阈值分割,虽然都改进了二维Otsu算法,但二者都需要在整个二维直方图上计算每条阈值直线的概率和类间离散矩阵的迹,因此都会影响计算效率.

萤火虫算法[11]是剑桥学者Xin-She Yang于2008年提出的一种较为新颖的生物进化算法,但是算法本身还是存在一些问题,例如收敛慢,易陷入局部最优等.同时很多学者也已经着手研究萤火虫算法在图像分割领域的应用.Horng Ming-Huwi[12]等结合萤火虫算法和最小交叉熵准则对图像进行多阈值分割,但是改进后的算法仍然存在计算复杂度高的问题.吴鹏[13]等提出了一种萤火虫算法优化最大熵的图像分割方法,但是该算法只考虑到图像的灰度概率信息,忽略了灰度值这一重要因素,所以结果都不尽理想.

为了更好地解决二维Otsu算法和萤火虫算法在图像分割优化中存在的复杂度高、实时性差等问题,本文提出了一种基于萤火虫算法改进的二维Otsu图像阈值分割方法.基本思想是将求解二维Otsu的目标函数问题转化为用萤火虫算法求解最优解问题,得出图像的最佳分割阈值,然后分割图像.实验结果表明,本文提出的算法分割效果理想、程序运行时间短.

1二维Otsu阈值分割方法

设有一幅灰度级为L的图像f(x,y),邻域平滑图像g(x,y)的灰度级也为L,g(x,y)中像素的灰度值为3×3邻域内的灰度均值.对于图像中的任意一个像素就可以由像素灰度值i和邻域平均灰度值j构成的二维单元来表示.假设,M为图像的总像素个数,fij为像素的灰度值为i而且邻域的平均灰度值为j的像素点的个数,那么二维单元(i,j)出现的概率为

(1)

任意给定一个阈值向量(s,t),将二维直方图分割成如图1中所示的A,B,C,D四个区域.其中,区域B和C表示图像中的目标类和背景类,区域A和D则对应与图像中的边缘点和噪声.分别用C1和C0来表示二维直方图中的目标类和背景类,其出现的概率分别表示为

(2)

(3)

图1　二维直方图

目标类C1和背景类C0对应的均值矢量μ1和μ0表示为

(4)

(5)

综合的灰度均值矢量μt可表示为

(6)

图像中边缘点或噪声的概率在多数情况下可以忽略.因此:

(7)

类间离散度矩阵表示为

(8)

背景类和目标类的距离测度函数可以用离散度矩阵的迹来表示:

(9)

当距离测度函数rtr(S)取得最大值时的阈值向量(s,t)即为最佳阈值.

在图像分割过程中,阈值的选取是最关键的环节,对于传统的二维Otsu阈值分割方法来说,在实时处理过程中效果不理想,因此本文引入了萤火虫算法来改进图像分割阈值的寻优过程.

2萤火虫算法

2.1基本萤火虫算法

萤火虫算法(Firefly Algorithm,FA)作为一种生物进化算法,其原理是利用萤火虫的发光特性,在指定区域内搜索其他个体并向亮度较大的个体靠近,从而实现其位置的寻优[14].萤火虫的个体信息主要是位置、亮度和吸引度,而导致萤火虫个体之间相互吸引移动的因素是亮度和吸引度.

从数学角度对萤火虫算法的描述如下:

萤火虫的相对荧光亮度I定义为

(10)

式中:I0代表萤火虫的最大萤光亮度值;γ为光强吸收系数;Rj为萤火虫i与j之间的空间距离.

萤火虫的吸引度β定义为

(11)

式中:β0表示萤火虫的最大吸引度,β0∈[0,1];γ、Rj意义同上.

萤火虫i在被吸引向萤火虫j移动的位置更新公式如下:

(12)

Xi(t)、Xj(t)为萤火虫i和j在第t次迭代时的位置向量;α为步长因子,且α∈[0,1];rand∈U(0,1)为随机因子.式中,Xi(t)为萤火虫当前时刻位置对下一时刻位置的影响,它能够有效地起到平衡全局和局部搜索的作用;β0e-γ Rj(Xj(t)-Xi(t))反映了群体中萤火虫个体之间由于相互吸引而引起的位置变化;α(rand-1/2)是为了避免萤火虫算法的搜索结果陷入局部最优而设置的随机步长项.

2.2基于自适应惯性权重优化的萤火虫算法

考虑到在传统萤火虫算法迭代后期算法已基本收敛到全局或者局部极值点附近,由式(11)可知,萤火虫之间的吸引力与相互之间的距离成反比作用,萤火虫算法的局部搜索能力下降甚至会在极值点附近震荡.虽然在萤火虫算法过程当中已经加入了随机项来防止震荡现象的发生,但是可能需要多次迭代之后算法才能摆脱极值点的束缚,因此在迭代次数有限时可能就无法找到全局最优值.为了解决上述问题,本文引入惯性权重来优化萤火虫算法,简称IFA算法,优化后的萤火虫算法如下:

(13)

ω即为本文引入的惯性权重(ω∈[0,1]),它决定本次迭代过程中萤火虫所处的位置受上次迭代结果影响的大小,惯性权重的计算公式如下:

(14)

式中:k为萤火虫更新位置的次数;f(Xi(k))为第i个萤火虫第k次更新位置时对应的目标函数值;f(Xbest(k))为第k次更新位置时最优萤火虫所对应的目标函数值,λ(k)的值反映出了惯性权重变化的平滑度,当其值变化较大时说明平滑度较差,反之亦然.由式(14)可知λ(k)的值会随着目标函数值的变化而改变,从而避免了权重的盲目选择,使得萤火虫算法的搜索方向更加合理.

为了平滑权重的变化,采用下式计算权重.

(15)

当算法的搜索结果接近极值点,λ(k)的变化速度明显减小,由式(15)可知ω(k)的值也越小,从而增强了算法的局部搜索能力,防止算法陷入极值点震荡的问题.反之,当算法搜索结果偏离极值点时,λ(k)变化加快,ω(k)越大,能够更快的收敛到极值点.

优化后的萤火虫算法(IFA)在保持萤火虫算法特性的基础上又加快了算法收敛速度,提高了算法精度,因此本文引入了IFA算法对二维Otsu阈值分割方法进行优化和求解.

3基于IFA算法的二维Otsu图像阈值分割方法

3.1IFA算法和二维Otsu图像阈值分割方法的结合

提出了一种基于IFA算法的二维Otsu图像阈值分割方法,通过引入改进的萤火虫算法对二维Otsu算法进行改进,将二维Otsu阈值分割方法的阈值(s,t)的选取问题转化为萤火虫算法对二维Otsu算法的距离测度函数式(9)的寻优问题.

(16)

为全局最优值.

将二维Otsu算法的距离测度函数rt r(S)设为萤火虫算法的目标函数,当rt r(S)取最大时的阈值(s,t),即为所求的图像最佳分割阈值.在对萤火虫算法进行计算之前设定如下三个前提条件:①萤火虫不分雌雄,发光弱者被发光强者吸引而移动.②每个萤火虫的吸引度β和发光强度I成正比.③距离测度函数rt r(S)的值对应于萤火虫的荧光亮度I.

3.2基于IFA算法的阈值流程图和寻优步骤

基于IFA算法的二维Otsu图像阈值分割方法流程图如图2所示.

图2　基于IFA算法的二维Otsu图像阈值分割方法流程图

具体步骤如下:

(1) 在搜索范围内随机放置萤火虫的个数m,设定每个萤火虫的最大吸引度为β0,传播介质的光强吸收系数为γ,随机步长因子的大小为α,最大迭代次数为T,随机初始化各萤火虫的位置.

(2) 计算萤火虫的荧光亮度.运用二维Otsu算法的距离测度函数rt r(S)计算目标函数值,并作为相应个体的最大萤光亮度值I0结合到改进的萤火虫算法中.

(3) 更新萤火虫i的位置.萤火虫i在被荧光亮度更高的萤火虫j吸引后的位置更新变化公式如式(12)所示.

(4) 通过距离测度函数rt r(S)计算位置更新后的萤火虫亮度值I0,并对荧光亮度最强的个体进行局部范围搜索,当目标值得到改善时则更新最优解,否则维持原来的最优解.

(5) 当达到最大迭代次数T时,记录此时的最优解Hbest,否则,重复步骤(3)～步骤(5)进入下一次搜索.最优解所对应的阈值(s,t)即为全局最优的图像分割阈值.

4实验结果及分析

本文采用了MATLAB 7.12.0(R2011a)编程环境,在硬件配置为Pentium(R) Dual-Core CPU 3.00 GHz,2 G内存的计算机上完成了仿真.

实验1测试IFA算法寻优性能.采用如下两个函数,全部取二维.

函数F1的全局极小值在0附近,fmin=0,初始范围(-4,4),n=2;函数F2的全局极小值在1附近,fmin=0,初始范围(-2.048,2.048),n=2.设FA和IFA的种群规模为80,迭代次数为50,光强系数γ=1,初始吸引度β0=1,随机移动步长因子α=0.2.IFA中的权重系数动态获取.

函数的收敛曲线图如图3、图4所示.

从图3、图4中可看出,两种算法在优化初期,种群分布均表现出了明显的随机特性;迭代后期两种算法均能收敛至极值点,寻优成功,但改进后的自适应惯性权重萤火虫算法(IFA)优化函数时收敛速度更快,具有更好的有效性和快速性.

实验2使用传统的二维Otsu方法和IFA算法改进后的二维Otsu方法对预处理后的图像进行分割比较.实验参数:光强系数γ=1,初始吸引度β0=1,步长因子α=0.5,萤火虫个数m=50,最大迭代次数T=50.仿真结果如图5～图7.

图3　优化函数F1的收敛曲线图

图4　优化函数F2的收敛曲线图

图5　迎客松原始图及分割结果

实验结果图像依次分别为原始图片,传统的二维Otsu方法分割结果 ,改进后的二维Otsu方法分割结果,图像的二维直方图.

传统的二维Otsu方法和改进后的二维Otsu方法的运行时间和分割阈值比较如表1所示.

不同参数设置对分割结果和速度的影响的实验,针对Rice图,对比的参数变动,其他参数按照实验默认值.

图6　Lenna原始图及分割结果

图7　Rice原始图及分割结果

表1　传统的二维Otsu方法和改进后的二维Otsu方法的运行时间及分割阈值对比

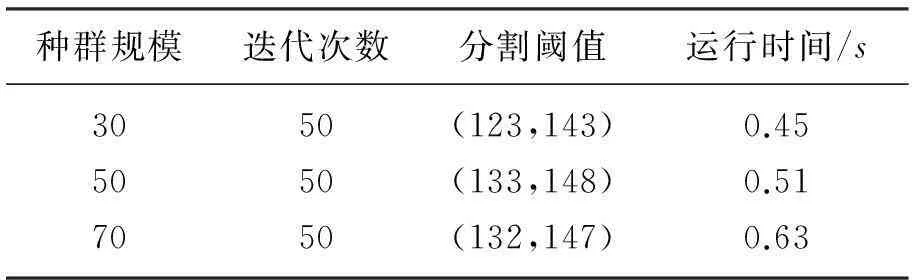
表2　种群规模对算法性能的影响

表3　步长因子α、光强度系数γ对算法性能的影响

从表2、表3可见, 实验参数对结果有一定的影响,综合各种因素, 本文选取的实验参数较优. 从图5～图7可以看出, 基于IFA改进后的二维Otsu方法的分割结果与传统的二维Otsu方法的分割结果差别不大, 且都能较好地选取阈值, 使目标与背景分割准确, 有效地减少图像误分割区域. 同时, 从表1可以看出,改进后的算法能够有效地缩短图像分割的运行时间,很好地改善传统二维Otsu方法的不足.

5总结

本文提出的基于IFA改进的二维Otsu图像阈值分割方法,在继承萤火虫算法的参数设置少,操作简单,稳定性好,寻优效果好等优点的基础上优化了萤火虫算法,然后对二维Otsu算法进行了改进.实验证明,基于IFA改进后的二维Otsu算法在保证分割效果的基础上改善了算法运算速度,具有很好的应用前景.

参考文献:

[1] SEZGIN M, SANKUR B. Survey over image threshold techniques and quantitative performance evaluation[J]. Journal of Electronic Imaging, 2004,13(1):146-168.

[2] 韩思奇,王蕾. 图像分割的阈值法综述[J]. 系统工程与电子技术, 2002,24(6):91-94,102.

(HAN S Q, WANG L. A Survey of thresholding methods for image segmentation[J]. Systems Engineering and Electronics, 2002, 24(6):91-94,102.)

[3] 刘雅坤,于双元,罗四维. 基于最小最大割算法的阈值分割算法[J]. 计算机科学, 2014,41(1):95-99.

(LIU Y K, YU S Y, LUO S W. Threshold image segmentation based on min-max cut algorithm[J]. Computer Science, 2014,41(1):95-99.)

[4] 方晶晶,李振波,姜宇. 人体肤色区域的自适应模型分割方法[J]. 计算机辅助设计与图形学学报, 2013,25(2):229-234.

(FANG J J, LI Z B, JIANG Y. Human skin color region segmentation based on adaptive model[J]. Journal of Computer-Aided Design & Computer Graphics, 2013,25(2):229-234.)

[5] 向方,王宏福. 图像边缘分割算法的优化研究与仿真[J]. 计算机仿真, 2011,28(8):280-283.

(XIANG F, WANG H F. The optimization of image edge segmentation algorithm research and simulation[J]. Computer Simulation, 2011,28(8):280-283.)

[6] OTSU N. A threshold selection method from gray-level histograms[J]. IEEE Transactions on Systems, Man, and Cybernetic, 1979,9(1):62-66.

[7] 范立南,胡向丽,孙申申. 基于OTSU算法和带通滤波器的毛玻璃型肺结节检测[J]. 沈阳大学学报(自然科学版), 2012,24(6):43-46.

(FAN L N, HU X L, SUN S S. Detection of ground glass opacity nodule based on Otsu algorithm and band-pass filter[J]. Journal of Shenyang University (Natural Science), 2012,24(6):43-46.)

[8] 刘健庄,栗文青. 灰度图像的二维Otsu自动阈值分割方法[J]. 自动化学报, 1993,19(1):101-105.

(LIU J Z, LI W Q. The automatic threshold of gray-level pictures via two-dimensional Otsu method[J]. Acta Automatica Sinica, 1993,19(1):101-105.)

[9] 范九伦,赵凤. 灰度图像的二维Otsu曲线阈值分割法[J]. 电子学报, 2007,35(4):751-755.

(FAN J L, ZHAO F. Two-dimensional Otsu’s curve thresholding segmentation method for gray-level images[J]. Acta Electronica Sinica, 2007,35(4):751-755.)

[10] 吴一全,潘喆,吴文怡. 二维直方图区域斜分阈值分割及快速递推算法[J]. 通信学报, 2008,29(4):77-83,89.

(WU Y Q, PAN Z, WU W Y. Image thresholding based on two-dimensional histogram oblique segmentation and its fast recurring algorithm[J]. Journal on Communications, 2008,29(4):77-83,89.)

[11] COELHO L, MARIANI V C. Improved firefly algorithm approach applied to chiller loading for energy conservation[J]. Energy and Buildings, 2013,59(2):273-278.

[12] HORNG M H, LIOU R J. Multilevel minimum cross entropy threshold selection based on the firefly algorithm[J]. Expert Systems with Applications, 2011,38(12):14805-14811.

[13] 吴鹏. 萤火虫算法优化最大熵的图像分割方法[J]. 计算机工程与应用, 2014(12):115-119.

(WU P. Image segmentation method based on firefly algorithm and maximum entropy method[J]. Computer Engineering and Applications, 2014(12):115-119.)

[14] YANG X S. Firefly algorithm for multimodal optimization[C]∥Stochastic Algorithms: Foundations and Applications, SAGA 2009, Lecture Notes in Computer Sciences, 2009,5792:169-178.

【责任编辑: 李艳】

Image Thresholding Segmentation with 2-D Otsu Based on Improved Firefly Algorithm

ZhouChenhang1,TianLiwei2,ZhaoHongwei2

(1. College of Information Engineering, Shenyang University, Shenyang 110044, China; 2. Liaoning Information Integration Technology Engineering Research Center of Internet of Things, Shenyang 110044, China)

Abstract:The research status of 2-D Otsu algorithm and the firefly algorithm is investigated. In order to solve the problems in 2-D image thresholding segmentation such as high computation cost, bad real time capability, etc, a novel image segmentation algorithm is proposed, that combing improved firefly algorithm with 2-D Otsu. The algorithm takes advantage of firefly algorithm that optimized by adaptive inertia weight (IFA)to search the optimal threshold of image segmentation. Experimental results show that the improved algorithm can achieve good segmentation performance, which may not only shorten the run time, but also be applied to the real-time processing of image segmentation.

Key words:optimal threshold; 2-D Otsu; inertia weight; firefly algorithm; image segmentation

中图分类号:TP 391.4

文献标志码:A

文章编号:2095-5456(2016)01-0045-06

作者简介:周晨航(1990-),男,安徽黄山人,沈阳大学硕士研究生; 田力威(1973-),男,辽宁沈阳人,沈阳大学教授,博士后研究人员.

基金项目:科学技术部国际科技合作与交流专项基金资助项目(2011DFA91810-5); 辽宁省自然科学基金资助项目(2013020011); 教育部新世纪优秀人才支持计划资助项目(NCET-12-1012).

收稿日期:2015-06-26