基于T-S模型的模糊时滞系统混杂输出控制
杨 红, 李 猛, 宋 健, 姚正刚, 马旭东
(沈阳大学 信息工程学院, 辽宁 沈阳 110044)
基于T-S模型的模糊时滞系统混杂输出控制
杨红, 李猛, 宋健, 姚正刚, 马旭东
(沈阳大学 信息工程学院, 辽宁 沈阳110044)
摘要:通过切换技术研究了基于T-S模型的模糊时滞系统混杂输出反馈镇定问题.利用多Lyapunov函数,基于线性矩阵不等式(LMI)设计了混杂输出反馈控制器,给出了相应的使得系统镇定的切换律设计方案.尽管单一连续的输出反馈控制器不能使系统稳定,但在指定的控制器中进行控制器切换可使系统镇定.仿真实验验证了该设计方法的可行性及有效性.
关键词:模糊; 时滞; 混杂; 输出反馈; 线性矩阵不等式
在实际工业领域,控制系统越来越多是非线性的,因此可以采用T-S模糊模型对其建立数学模型.对于任何一个系统而言,稳定性是对其做各种研究的前提条件,那么模糊系统的稳定性研究也一直是模糊控制领域中的热点问题.近年来对于模糊系统稳定分析所得到的成果层出不穷[1-6],但是许多成果都是运用状态反馈对其进行的控制研究,而在一些状态不完全可测的系统中通过状态反馈进行控制就显得无能为力.目前,有关于模糊系统输出反馈的研究成果并不多见[7-10],针对模糊时滞系统研究其输出反馈的文献更加有限.
当系统的状态反馈控制器在物理上不能够完全被实现,且在一些具有不确定性的情况下无法测得系统每一时刻的状态时,就需要考虑输出反馈控制器.进一步,当一个单一的输出反馈控制器不能镇定系统时,可考虑在指定的输出反馈控制器间进行切换达到镇定系统的目的.本文是基于混杂控制的思想,通过Lyapunov稳定性理论给出了模糊时滞系统的鲁棒可镇定条件及其切换律的设计方案,来研究模糊时滞系统的混杂输出反馈控制问题的.
1问题描述
基于T-S模型,模糊时滞系统可描述为
Ri:ifZ1(t) isMi1and…andZg(t) isMig,then.
(1)
其中,i=1,2,…,r.
这里Ri表示T-S模糊模型的第i条规则.Z1(t),…,Zs(t)代表模糊规则的前件变量,Mi1,…,Mig描述为模糊集合,x(t)∈Rn是状态变量,u(t)∈Rm是控制输入,Ai1,Ai2是适当维数的时常数矩阵,τ>0表示时间滞后常数,φ(t)是实值连续向量函数.
则式(1)的全局模型为
μis(zs(t))表示前件变量zs(t) 对应于模糊集Mis的隶属度.
现在假设存在m个指定的输出反馈控制器,系统(2)的控制器可以在m个输出反馈控制器中切换,则系统(2)可以被描述为
(3)
这里F1i,…,Fmi为已知矩阵.其中,分段常值函数σ(x(·))=σ:R+→M={1,2,…,m}是一个待设计的切换信号.
考虑控制器在u1(t),u2(t),…,um(t)之间相互切换,即混杂输出反馈控制
(4)
这里
则模糊时滞系统的数学模型可描述为
(5)
假设控制器的个数m=2.采用多Lyapunov函数方法,给出切换律σ:[0,+∞)→{1,2}的设计方案,使得在此切换律下,模糊时滞系统(5)渐近稳定.
定理1假设存在非负或非正实数βσ和正定对称矩阵P1和P2,以及正定对称矩阵Q,使得下面的矩阵不等式成立
(6)
(7)
则一定存在切换律σ:[0,+∞)→{1,2},使得系统(5)渐近稳定.
证明不失一般性,假设βσij>0,根据S-procedure,有
如果xT(P2-P1)x≥0,且x≠0,那么
(8)
如果xT(P1-P2)x≥0,且x≠0, 那么
(9)
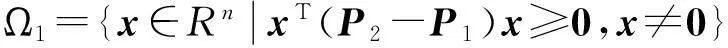
(10)
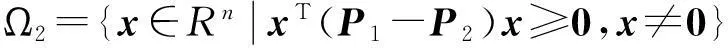
(11)
则Ω1∪Ω2=Rn{0}.考虑式(10)和式(11),设计切换律如下:
(12)
选取Lyapunov-like函数如下:
其中,σ=1,2.P1和P2为对称正定矩阵,它们分别满足式(8)和式(9).
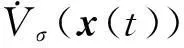
依据多Lyapunov函数技术,立即可以获得系统(5)的渐近稳定性.
2仿真例子
模糊时滞系统为
(13)
其中,
隶属度函数选取为:
利用MATLAB的LMITOOLBOX可解得
令
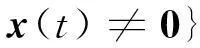
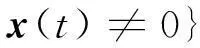
则Ω1∪Ω2=Rn{0}.下面给出切换律的设计:
(14)
那么系统(13)在切换律(14)下是渐近稳定的.取初始条件x(0)=[-5 5]T,Simulink仿真结果如图1所示.
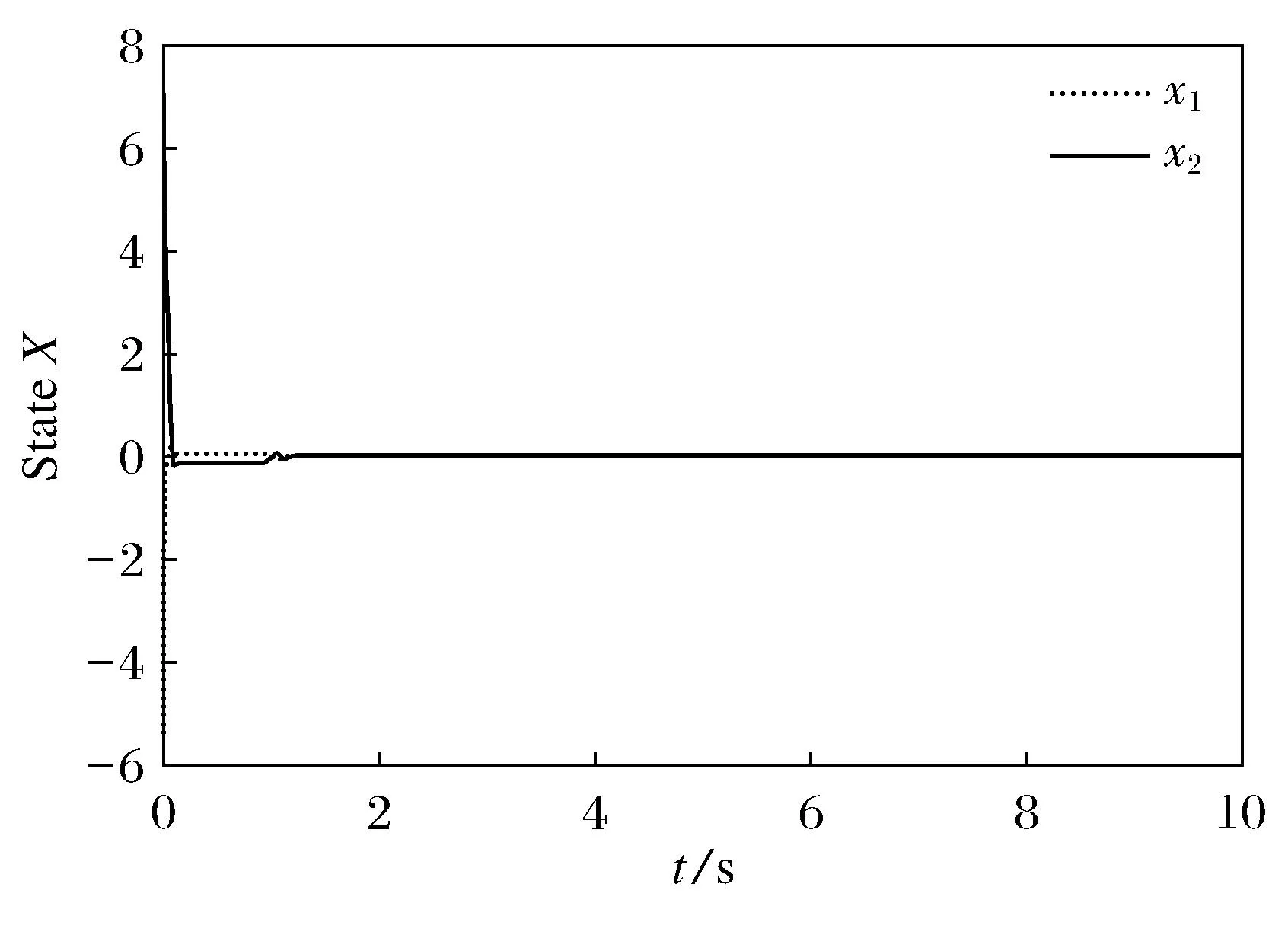
图1 输出反馈混杂控制的状态响应曲线
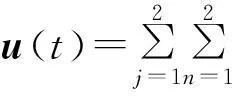
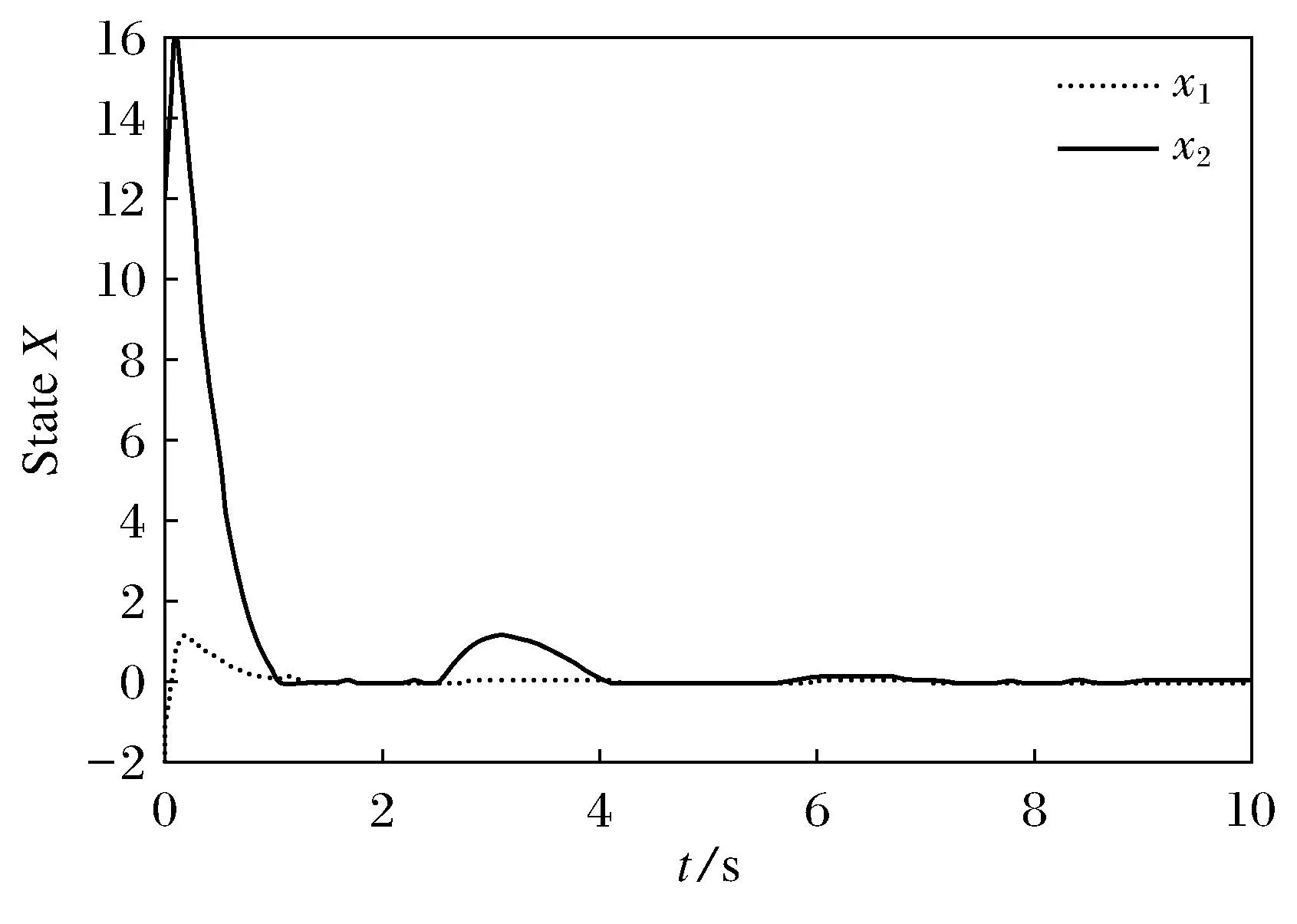
图2 传统输出反馈控制的状态响应曲线
由两图比较可以看出,图1的曲线性能指标要明显好于图2.
3结论
本文研究了模糊时滞系统的混杂输出反馈控制问题.如果在一个给定的输出反馈控制器集合中每个单一的控制器均不能使系统具有所希望的性能时,构造混杂输出反馈控制器.其核心思想是通过在允许的输出反馈控制器集合中备选的控制器之间选择切换以实现控制目的.所设计的切换策略为模糊时滞系统实现稳定提供了更多的可能.同时,能运用MATLAB工具箱方便地求解LMI.
参考文献:
[1] TAKAGI T,SUGENO M. Fuzzy identification of systems and its applications to modeling and control[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1985,15(1):116-132.
[2] FENG G. A survey on analysis and design of model-based fuzzy control systems[J]. IEEE Transactions on Fuzzy Systems, 2006, 14(5): 676-697.
[3] GAO H, CHEN T. Stabilization of nonlinear systems under variable sampling: A fuzzy control approach[J]. IEEE Transactions on Fuzzy Systems, 2007, 15(5): 972-983.
[4] TANAKA K, SUGENO M. Stability analysis and design of fuzzy control systems[J]. Fuzzy Sets and Systems, 1992, 45:135-156.
[5] CHEN C L. CHEN P C and CHEN C K. Analysis and design of fuzzy control system [J]. Fuzzy Sets and Systems, 1993,57 :125-140.
[6] KIM W C, ALM S C, KWON W H. Stability analysis and stabilization of fuzzy state space models[J], Fuzzy Sets and Systems, 1995, 71:131-142.
[7] OBERDIECK R, PISTIKOPOULOS E N, Explicit hybrid model-predictive control: The exact solution, Automatica, 2015, 58: 152-159.
[8] SEN M D L. On the robust adaptive stabilization of class of nominally first-order hybrid systems[J], IEEE Transactions on Automatic Control, 1999, 44(3): 597-602.
[9] ZHANG L, WU J. Reliable control for time-varying delay switched fuzzy systems with faulty actuators based on observers switching method[J]. Mathematical Problems in Engineering, 2013, 20(1):14-26.
[10] 吕欢欢, 杨红. 控制器切换下不确定模糊系统的输出反馈[J]. 沈阳大学学报(自然科学版), 2013, 25 (6): 472-475.
(LYU H H , YANG H. Output feedback research on uncertain fuzzy systems under controller switching[J]. Journal of Shenyang University(Natural Science) , 2013, 25(6), 472-475.)
【责任编辑: 肖景魁】
Output Hybrid Control for a Class of Fuzzy Time-Delay Systems Based on T-S Model
YangHong,LiMeng,SongJian,YaoZhenggang,MaXudong
(School of Information Engineering, Shenyang University, Shenyang 110044, China)
Abstract:By switching technology, the problem of hybrid output feedback control based on T-S model for fuzzy time-delay system is considered. Using the multiple Lyapunov function methods, based on linear matrix inequality (LMI), hybrid output feedback controllers are designed, and the design scheme of the switching laws which make the system asymptotic stability is presented. The results show that though none of individual continuous output feedback controllers makes system stabilizable, the stability can be realized via switching between finite candidate controllers. A comparing simulation demonstrates the feasibility and the effectiveness of the proposed method.
Key words:fuzzy; time-delay; hybrid; output feedback; LMI
中图分类号:O 231
文献标志码:A
文章编号:2095-5456(2016)01-0041-04
作者简介:杨红(1978-),女,辽宁沈阳人,沈阳大学副教授,博士.
基金项目:国家自然科学基金资助项目(61004039); 辽宁省高等学校杰出青年学者成长计划资助项目(LJQ2013123).
收稿日期:2015-06-09

