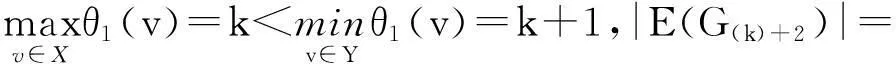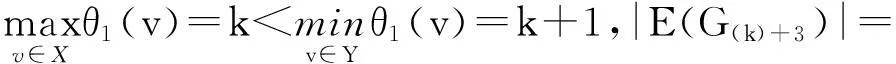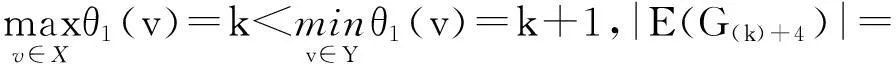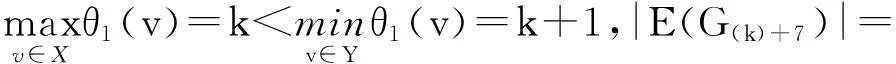非连通图D2,4∪G的优美标号
吴 跃 生
(华东交通大学 理学院, 江西 南昌 330013)
非连通图D2,4∪G的优美标号
吴 跃 生
(华东交通大学 理学院, 江西 南昌330013)
摘要:讨论了非连通图D2,4∪G的优美性,给出了非连通图D2,4∪G是优美图的六个充分条件.证明了非连通图D2,4∪G(k)+a(a=2,3,4,5,6,7)都是优美的.
关键词:优美图; 交错图; 非连通图; 优美标号
记号V(G)和E(G)分别表示图G的顶点集和边集,m和n均为非负整数,且满足0≤m 图的优美标号问题是组合数学中一个热门课题[1-13].文献[4-13]研究了非连通图的优美性,文献[4]研究了非连通图C4m∪G的优美性;文献[6-8]研究了非连通图C4m-1∪G的优美性;文献[9-10]分别研究了非流通图D2,6∪G和非流通图D2,8∪G的优美标号;文献[11-13]研究了非连通图C4m-1∪C12m-8∪G的优美性. 1相关概念 定义1[1]对于一个图G=(V,E),称G是优美图,θ是G的一组优美标号是指:如果存在一个单射θ: V(G)→[0, |E(G)|]使得对所有边e=uv∈E(G),由θ′(e)=|θ(u)-θ(v)|导出的E(G)→[1,|E(G)|]是一个双射. 把任意m个圈Cn的恰有一个公共点所组成的图记作Dm,n[1]. D2,4存在特征为2,且 缺4和7标号值的交错标号,如图1所示,为方便记,把如图1所示的标号记为:(1:8,0,6;5,2,3) 图1 图D2,4的交错标号 本文讨论了非连通图D2,4∪G的优美性. 2主要结果及其证明 定理1当2≤k+2≤|E(G(k)+2)|)时,非连通图D2,4∪G(k)+2存在下列标号: (1) 特征为k+4且缺k+1和k+6标号值的交错标号; (2) 特征为k+3且缺k+6和k+8标号值的交错标号; (3) 缺k+3和k+7标号值的优美标号; (4) 缺k+1和k+5标号值的优美标号. 图2 图D2,4 非连通图D2,4∪G(k)+2的各种顶点标号θ定义为 下面证明第一种标号θ是非连通图D2,4∪G(k)+2的优美标号. (1) θ:X→[0, k]是单射(或双射); θ:Y→[k+9,q+8]-{k+10}是单射; θ:V(D2,4)→[k+2,k+10]-{k+6,k+9}是双射; 容易验证:θ: V(D2,4∪G(k)+2)→[0, q+8]-{k+1,k+6}是单射. (2) θ′(v1v2)=|θ(v1)-θ(v2)|=6,θ′(v2v3)=|θ(v2)-θ(v3)|=5,θ′(v1v4)=|θ(v1)-θ(v4)|=8, θ′(v3v4)=|θ(v3)-θ(v4)|=7,θ′(v3v5)=|θ(v3)-θ(v5)|=4,θ′(v5v6)=|θ(v5)-θ(v6)|=3, θ′(v3v7)=|θ(v3)-θ(v7)|=2,θ′(v6v7)=|θ(v6)-θ(v7)|=1, θ′:E(D2,4)→[1,8]是双射; θ′:E(G(k)+2)→[9,q+8]是双射. θ′:E(D2,4∪G(k)+2)→[1, q+8]是一一对应. 由(1)和(2)可知第一种标号θ就是非连通图D2,4∪G(k)+2的缺k+1和k+6标号值的优美标号. 令X1=X∪{v1,v3,v6},Y1=Y∪{v2,v4,v5,v7} 所以,第一种标号θ就是非连通图D2,4∪G(k)+2的特征为k+4,且缺k+1和k+6标号值的交错标号. 其他各种标号的证明可仿上. 证毕. 以下定理只给出标号, 定理证明与定理1的过程类似,故省略. 定理2当3≤k+3≤|E(G(k)+3)|)时,非连通图D2,4∪G(k)+3存在下列优美标号: (1) 特征为k+4且缺k+1和k+7标号值的交错标号. (2) 特征为k+4且缺k+6和k+8标号值的交错标号. 非连通图D2,4∪G(k)+3的各种顶点标号θ定义为 定理3当4≤k+4≤|E(G(k)+4)|)时,非连通图D2,4∪G(k)+4存在下列优美标号: (1) 缺k+1和k+3标号值的优美标号; (2) 特征为5缺k+1和k+7标号值的交错标号; (3) 缺k+5和k+6标号值的优美标号. 非连通图D2,4∪G(k)+4的各种顶点标号θ定义为 定理4当5≤k+5≤|E(G(k)+5)|)时,非连通图D2,4∪G(k)+5存在下列优美标号: (1) 缺k+2和k+8标号值的优美标号; (2) 缺k+1和k+3标号值的优美标号. 非连通图D2,4∪G(k)+5的各种顶点标号θ定义为 定理5当6≤k+6≤|E(G(k)+6)|)时,非连通图D2,4∪G(k)+6存在下列优美标号: (1) 缺k+4和k+7标号值的优美标号; (2) 缺k+1和k+3标号值的优美标号; (3) 缺k+3和k+8标号值的优美标号; (4) 缺k+2和k+8标号值的优美标号; (5) 缺k+5和k+7标号值的优美标号; (6) 缺k+1和k+3标号值的优美标号; (7) 缺k+4和k+8标号值的优美标号. 非连通图D2,4∪G(k)+6的各种顶点标号θ定义为: 定理6当7≤k+7≤|E(G(k)+7)|)时,非连通图D2,4∪G(k)+7存在下列优美标号: (1) 缺k+1和k+4标号值的优美标号; (2) 缺k+1和k+3标号值的优美标号; (3) 缺k+2和k+3标号值的优美标号; (4) 缺k+1和k+5标号值的优美标号. 定义非连通图D2,4∪G(k)+7的各种顶点标号θ为: 3结论 本文讨论了非连通图D2,4∪G的优美性,给出了非连通图D2,4∪G是优美图的六个充分条件.证明了非连通图D2,4∪G(k)+a(a=2,3,4,5,6,7)都是优美的,可为继续研究非连通图Dm,n∪G的优美性提供借鉴. 参考文献: [1] 马克杰. 优美图[M]. 北京:北京大学出版社, 1991:1-247. (MAKJ.Gracefulgraph[M].Beijing:PekingUniversityPress, 1991:1-247.) [2] 杨显文. 关于C4m蛇的优美性[J].工程数学学报, 1995,12(4):108-112. (YANG X W. OnC4m-snakes' gratefulness[J]. Journal of Engineering Mathematics, 1995,12(4):108-112.) [3] GALLIAN J A. A dynamic survey of graph labeling[J]. The Electronic Journal of Combinatorics, 2013,16:1-308.) [4] 吴跃生,王广富,徐保根. 非连通图C4m∪G的优美标号[J]. 重庆师范大学学报(自然科学版), 2015,32(2):79-83. (WU Y S, WANG G F, XU B G. The graceful labeling of the unconnected graphC4m∪G[J]. Journal of Chongqing Normal University(Natural Science), 2015,32(2):79-83.) [5] 吴跃生. 非连通图G+e∪Hk-1的优美性[J].吉首大学学报(自然科学版), 2014,35(2):3-5. (WU Y S. The graceful labeling of the unconnected graphG+e∪Hk-1[J]. Journal of Jishou University(Natural Science), 2014,35(2):3-5.) [6] 吴跃生. 非连通图C4m-1∪G的优美标号[J]. 吉首大学学报(自然科学版), 2014,35(3):1-3. (WU Y S. The graceful labeling of the unconnected graphC4m-1∪G[J]. Journal of Jishou University (Natural Science), 2014,35(3):1-3. [7] 吴跃生. 再探非连通图C4m-1∪G的优美标号[J]. 吉首大学学报(自然科学版), 2015,36(1):1-4. (WU Y S. Revisiting the graceful labeling of the unconnected graphC4m-1∪G[J]. Journal of Jishou University(Natural Science), 2015,36(1):1-4. [8] 吴跃生. 三探非连通图C4m-1∪G的优美标号[J]. 吉首大学学报(自然科学版), 2015,36(4):5-8. (WU Y S. Further exploration the graceful labeling of the unconnected graphC4m-1∪G[J]. Journal of Jishou University (Natural Science), 2015,36(4):5-8. [9] 吴跃生.非连通图D2,6∪G的优美标号[J] .海南大学学报(自然科学版), 2014,32(1):32-34. (WU Y S. Graceful labeling of unconnected graphD2,6∪G[J]. Journal of Hainan University (Natural Science ), 2014,32(1):32-34.) [10] 吴跃生. 非连通图D2,8∪G的优美标号[J]. 西华师范大学学报(自然科学版), 2014,35(1):4-6. (WU Y S. The graceful labeling of unconnected graphD2,8∪G[J]. Journal of China West Normal University (Natural Science), 2014,35(1):4-6.) [11] 吴跃生. 非连通图C4m-1∪C12m-8∪G的优美性[J]. 沈阳大学学报(自然科学版), 2014,26(4):334-337. (WU Y S. Graceful labeling of unconnected graphC4m-1∪C12m-8∪G[J]. Journal of Shenyang University (Natural Science), 2014,26(1):334-337.) [12] 吴跃生. 再探非连通图C4m-1∪C12m-8∪G的优美性[J]. 沈阳大学学报(自然科学版), 2015,27(1):72-76. (WU Y S. Further discussion on graceful labeling of unconnected graphC4m-1∪C12m-8∪G[J]. Journal of Shenyang University(Natural Science), 2015,27(1):72-76.) [13] 吴跃生.三探非连通图C4m-1∪C12m-8∪G的优美性[J]. 沈阳大学学报(自然科学版), 2015,27(5):420-425. (WU Y S. Further Third discussion on graceful labeling of unconnected graphC4m-1∪C12m-8∪G[J]. Journal of Shenyang University (Natural Science), 2015,27(5):420-425.) [14] 吴跃生. 非连通L5∪G的优美标号[J]. 西华大学学报(自然科学版), 2015,34(2):30-35. (WU Y S. The graceful labeling of the unconnected graphL5∪G[J]. Journal of Xihua University (Natural Science), 2015,34(2):30-35.) 【责任编辑: 肖景魁】 Graceful Labeling of Unconnected GraphD2,4∪G WuYuesheng (School of Science, East ChinaJiaotong University, Nanchang 330013, China ) Abstract:The gracefulness of the unconnected graph D2,4∪G is discussed. Six sufficient conditions are given for the gracefulness of unconnected graph D2,4∪G. It proves that the graph D2,4∪G(k)+aare graceful graph for a=2,3,4,5,6,7. Key words:graceful graph; alternating graph; unconnected graph; graceful labeling 中图分类号:O 157.5 文献标志码:A 文章编号:2095-5456(2016)01-0078-04 作者简介:吴跃生(1959-),男,江西瑞金人,华东交通大学副教授. 基金项目:国家自然科学基金资助项目(11261019,11361024). 收稿日期:2015-09-08