碳纳米管内嵌多种碳分子的密度泛函计算分析
高 鹭 远
(沈阳大学 师范学院, 辽宁 沈阳 110003)
碳纳米管内嵌多种碳分子的密度泛函计算分析
高 鹭 远
(沈阳大学 师范学院, 辽宁 沈阳110003)
摘要:从量子化学角度分析了在不同直径的碳纳米管(CNT管)里内嵌碳链、碳环、碳碗、碳笼、碳管和石墨片等碳分子所形成的碳素纳米复合结构.通过赝势平面波方法对上述体系进行了几何构型的优化,并采用相关与交换相结合的密度泛函(PBE)方法计算它们的结构、总能量、能带结构、态密度、电-声耦合参数及振动频率等.
关键词:碳链; 碳环; 碳碗; 碳笼; 石墨片; 碳纳米管
自从富勒烯、碳纳米管及碳纳米豆荚等碳素纳米结构问世以来,它们即成为纳米科技与纳米材料领域里被广泛关注的焦点.其应用范围涉及到电子、机械、医药、能源、化工等工业技术领域;并且对航空、航天、高温超导、生物工程、生物医学、微电子技术等高科技领域的科学研究也将产生重要的影响.
为了寻求新型碳素纳米复合结构, 探究其材料学性能, 特选择将多种碳分子嵌入至不同管径的碳纳米管中作为研究课题, 从理论上研究这些结构的特征与性能, 以期在这个领域的理论研究方面做一些具有前瞻性的工作. 该研究采用密度泛函(DF)方法并结合分子动力学(MD)探究封闭在小管径纳米管(CNT)里的各种碳分子的结构与性质. 迄今已相继对直径从0.553 nm的(4,4)到0.953 nm的(7,7)纳米管内嵌碳链、碳环、石墨片、石墨碗、石墨笼和石墨管等形成复合结构的能量、几何构型和振动性质做过理论计算.
1研究方法
采用“模拟退火”DF计算研究方法,以Troullier和Martins形式的离子赝势,描述了电子-离子相互作用,交换相关能采用的是Perdew、Burke和Ernzerhof(PBE)的近似值[1];计算中使用了布里渊区具有一个单点(k=0)的周期性边界条件,并且以具有50Ry动能截断的平面波基函数展开波函数.整个计算中选取一个正交单位晶胞,且纳米管(CNT)之间的间隔至少是0.8 nm.这种CNT的超晶胞模型包括5个单位晶胞:CNT(2,2)[40个碳原子]、(4,4)[80个碳原子]、(5,5)[100个碳原子]、(6,6)[120个碳原子]和(7,7)[140碳原子],且超晶胞沿着CNT轴向长约1.24 nm.被封闭的碳分子包括链、环、片、碗、笼和管等.对这些几何构型采用模拟退火的方式进行优化;之后以具有0.001 nm的原子位移之有限差值计算振动频率与特征向量.计算模型相关信息见表1.
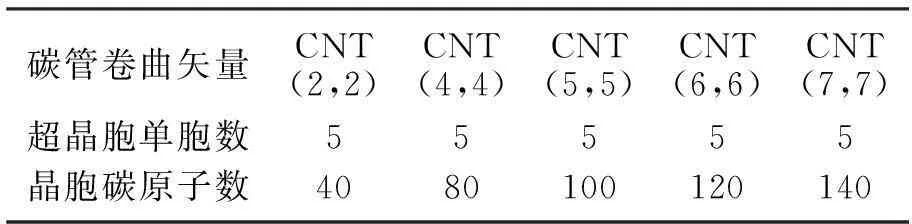
表1 计算模型相关信息
2计算结果的理论分析
2.1复合物的结构与能量
管内碳分子的相对稳定性取决于结合能的数值,结合能是指碳分子嵌入CNT前后总能量的差值,即:
(1)
Etot(csp)和Etot(CNT)分别是游离的碳分子和空CNT的总能量,Etot[csp@(CNT)]是碳分子与CNT复合结构的总能量.Ebind值越大意味着内嵌碳分子跟纳米管的结合越强.如果碳原子数目多于10个(无论是偶数还是奇数),则复合结构体系都按单重态计算;而少于10个碳原子的复合结构体系最稳定的构型:偶数碳应该是三重态,奇数碳则为单重态[2].在评估由方程(1)所得的Ebind时,采用的是Etot(csp)的最低能量值.扶手椅碳纳米管直径优化值见表2.

表2 扶手椅碳纳米管直径优化值
2.1.1碳链
线性碳链(n=2~6)的长度会影响到结合能,但链内碳原子间隔对其影响不大.对于CNT(5,5)而言,链内碳原子之间的最小间隔约为0.587 nm,就CNT(6,6)而言,这种间隔约为0.611 nm,故链内碳原子各间隔的相互影响可以忽略.从CNT(5,5)内的四原子链[可表示为链4@(5,5)]的几种不同初始几何构型开始进行结构优化,得到的最稳定构型同为一种沿着CNT轴分布的链,其结合能为-0.07 eV;其他初始构型,如一个远离中心位置而平行于轴的碳链和倾斜的碳链优化后也都为“同轴”几何构型;如果初始链的几何构型垂直于CNT轴,则迭代至下一个能量最小值时,存在一个较小的弛豫,但这种结构并没有成键,其结合能为-1.95 eV.连接链和CNT壁的三角形构型从能量角度而言是不利的,且部分原子有可能离开CNT壁.从双原子链到六原子链,当它们沿着CNT(5,5)轴方向嵌入时,碳链与CNT壁会部分成键或产生弱相互作用.另一方面当四原子链分别嵌入到直径为0.55 nm的CNT(4,4)到0.95 nm的CNT(7,7)等一系列的纳米管中形成复合结构时,过程的结合能逐渐趋于零.在纳米管CNT(4,4)里的链4与管壁的结合能具有较大的负值,这意味着CNT(4,4)的直径太小以致于不能容纳下线性碳链;在CNT(6,6)中,四原子链与管壁间微弱成键,而在CNT(5,5)和CNT(7,7)中,四原子链与管壁间仅存在弱相互作用;可以预见对于直径很大的CNT而言,结合能趋于零,表明在这种管里链与管壁间的相互作用很小.计算结果表明当把碳链嵌入到直径为0.684 nm CNT(5,5)时,碳管直径不变.共轴链与纳米管壁的间隙为0.342 nm,与石墨夹层间隔0.34 nm几乎相同,这与HRTEM测试结果不谋而合[3].该情况表明半径为0.35 nm的CNT和最里层半径为该值的MWNT一样均能内嵌碳链.为模拟一个无限长的碳链,把一个十原子的碳链分别嵌入到CNT(5,5)和CNT(7,7)里, 前者结合能是负值;而后者结合能则为正值.不能把十原子碳链的计算结果直接与短链进行比较,因为十原子碳链虚拟与超晶胞相当,这种紧束缚的松弛会导致较强的结合.在CNT(4,4)中四原子链内完全松弛的C—C键长是0.129 nm、0.134 nm和0.129 nm,这与十原子碳链内嵌的情况类似,均为改良的累积键.
2.1.2碳环、石墨片和碳碗
二维石墨片的每个超晶胞包括20~40个碳原子,当其嵌入到CNT中,经结构优化后,片20的结构由初始几何构型变为一条连接六边形的带子,在CNT(5,5)中会变小.边缘原子的悬空键会通过与CNT壁的结合而消除,那些边缘原子会朝着石墨片移动以形成双管或管片杂化的结构.片20嵌入到CNT(6,6)的中心,会导致六元环向六元环与八元环稠合形成多环结构的转变,这种多环结构成正方形.没有外部的CNT情况下,对连接的六边形结构优化显示.当处于封闭的几何构型时,初始的六元环稠合成十二元环且成正方形.可见几何构型按照释放张力的方式改变,且对于独立的碳原子团而言,类似的结构也已发现.另一方面,CNT管的半径变形源于指向片20和CNT(6,6)管之间的相互排斥作用.内嵌CNT(7,7)中心的六边形以类似于CNT(6,6)中的方式而松弛下来,此种情况CNT管的变形很小.这种六边形也可放置到靠近CNT(7,7)的管壁处,即远离中心的位置;这样会因松弛导致六元环与CNT管壁的插销式连接 (仅一条边结合到管壁上).这种情况类似于CNT(5,5)管中的情形.片20嵌入到CNT(5,5)管中时不能导致二者的结合,但当纳米管管径变大时,Ebind会逐渐增大.例如直径为0.953 nm的CNT(7,7)将达到0.39 eV.片20@CNT(7,7)的远离中心结构很不稳定,其结合能为-7.23 eV.
把石墨层的窄带嵌入到CNT(7,7)中,当石墨片小于外部容纳它的CNT管时,这些石墨片边缘的碳原子倾向于形成五边形非平面结构,因而在片的边缘消除了悬空键.当石墨片尺寸增大时,与石墨片边缘碳原子成键的管壁原子能被取代,这样既增大了纳米管的变形又增加了石墨片的弯曲度.石墨片内嵌CNT管形成的复合结构之结合能见表3.

表3 石墨片内嵌CNT管形成复合结构的结合能
从表3结合能数值看出,①所列结构中的最后一个[片40@ CNT(7,7)]应该最稳定,但与它的原始管结构相比较,复合结构的外管已完全扭曲;②复合结构[片25@ CNT(7,7)]很不稳定,然而这一点正是在多壁碳纳米管里所期望的.
石墨碗能由石墨片通过一个五边形取代六边形的方式得到.石墨碗20通过碗边缘碳原子与管壁原子间的结合,被锁定在CNT(7,7)管壁上.石墨碗20嵌入CNT(7,7)管中会导致CNT管变形,且结合能为负值(-3.40 eV).总的来看,重排饱和悬空键或与CNT壁直接成键,都会有利于石墨片和碗的内嵌过程;然而在形成复合结构过程中,石墨片、碗及碳纳米管的变形却又会阻碍这种内嵌过程.
2.1.3碳笼和碳管
实验上和理论上均已证实,碳笼C20球是富勒烯家族中最小的成员,它是由12个五边形组成的.笼20(C20) 已先后被嵌入到CNT(5,5)、CNT(6,6)、CNT(7,7)的中心[4-6].C20嵌入到CNT(5,5)中导致CNT的半径增大(变形),且结合能为负值(-25.54 eV),这对复合过程十分不利.随着纳米管半径增大这种复合过程中CNT的半径扩大(变形)会逐渐降低;从结合能看也会变得更加有利,例如直径为0.953 nm的CNT(7,7)管作为主体材料时,其结合能是-1.03 eV.笼20与CNT(7,7)之间的原子最小间隔约为0.283 nm,小于石墨夹层间隔.,当CNT管直径增加时,笼20(C20)与管的结合能趋于零.以上结果表明直径大于CNT(7,7)的纳米管均可容纳笼20以形成稳定的碳纳米豆荚.计算结果还同时表明,如果笼20具有一个远离中心位置而靠近CNT(7,7)管壁的初始构型,那么它会回到CNT(7,7)管里的中心位置,亦即后一种情况更为稳定.
对于双壁纳米管(DWNT)(2,2)@(7,7)结构中的CNT(2,2)而言,其直径优化值是0.30 nm,它比卷成筒状的石墨片的直径要大.(2,2)和(7,7)之间的原子最小间距约为0.336 nm,接近石墨夹层间隔0.34 nm.这种理论计算得到的几何构型与HRTEM测试结果一致.CNT(2,2)@(7,7)的结合能为-0.90 eV,如果把CNT(2,2) 展开成为石墨片(片40),其能量降低值为0.27 eV/原子.在嵌入CNT(7,7)后石墨片的每个碳原子的总能量比在CNT(2,2)中的能量要低0.08 eV.当石墨片40被嵌入到CNT(7,7)管中时,石墨片与CNT二者都将发生变形.由于附加约束的限制,在多壁纳米管中,最里边的纳米管变形很小,且石墨片40@(MWNT)复合体系的总能量将会增加.上述结果表明外层碳管会阻碍石墨片在碳管内形成;与形成SWNT(2,2)相比,这种阻碍更有利于在多壁纳米管的核心形成CNT(2,2).
上述有关碳纳米管内嵌多种碳分子形成复合体的结构与热力学研究表明, 纳米管的直径是影响结构稳定性及能量高低的重要因素.带有封闭物种(csp)的纳米管单重态复合体:①如果CNT的直径很小,则CNT与csp之间的相互作用将表现为排斥.在链4@CNT(4,4)中,这种情况就非常明显;并且当直径增加时,这种排斥作用会减小.②如果CNT的直径很大,则CNT与csp之间的相互作用和结合能都会很小.这种情况在包含有20个碳原子的碳链20、碳片20和碳笼20的内嵌中均非常明显.具有杂化键结合的四原子链会导致CNT的变形和能量上的不利. 从能量变化看,链4与CNT的结合能随纳米管的直径改变而改变,且链4嵌入到CNT(6,6)管中,结合能具有最大值.在Chain10@CNT(7,7)复合体中键的数目与原子的数目相同,但在Chain4@CNT(7,7)复合体中,键的数目要比原子数目少一个.因而在结合能上是前者大于后者.在所有计算过的复合体中,对于各种内嵌分子“远离轴”的初始结构,经优化后的结果都趋于同一种结构,即内嵌分子主对称轴与管轴相重合的所谓“轴向结构”.研究中发现在稳定链结构的过程中,CNT管起着实质性的作用;因为几乎所有独立结构的链都采取了具有虚频的弯曲振动模式. 在有关狭窄单壁纳米管中的4He的扩展蒙特卡罗(Monte Carlo)计算中,发现理想的一维体系与CNT管中相似的体系之间存在着差别.嵌入直径为0.684 nm的CNT(5,5)管中的碳链,在能量上比碳片和碳笼更为有利.虽然研究过的多种结构,从方程(1)角度看是“未结合”的,但是结合能随着CNT管直径变化而变化这一事实表明,比CNT(7,7)大的碳纳米管能够容纳碳链及比碳链更大的碳分子.例如,相互连接的碳环、碳笼20和纳米管(2,2)在CNT(7,7)中都具有一个小的结合能.对于有序的碳链、连接的环、CNT(2,2)和碳笼20而言,嵌入到CNT(7,7)中会变得越来越有利.研究中还发现,许多结构的成键特征异同寻常:2个、3个甚至4个完全等同的碳原子能共存于链管或片管的混合结构中,相应于sp、sp2和sp3杂化.除了起封闭作用外,碳纳米管还能提供与其他内嵌碳分子相互作用的壁原子.这些原子积累在CNT管壁上,形成具有混合杂化键的新分子或原子团.
2.2振动频率
对于上文提到过的所有结构均已做过振动频率计算.单壁扶手椅纳米管SWNT (5,5)的拉曼活性呼吸模式(BM)之频率(370 cm-1)与单壁螺旋纳米管SWNT (6,4)的紧束缚频率值(366 cm-1)十分接近,它们都具有类似的直径(0.69 nm).这种BM频率能够从反函数估算出来,而这种反函数是由力常数计算得到的.
(2)
式中:ω为振动频率反函数估算值,d为这种CNT管的直径,通常以nm作单位.运用该公式可预测SWNT(5,5)的频率为327 cm-1.对于小管径的CNT而言,这种从单一反函数计算得到的频率值与BM的偏差在其他DF计算中也是很明显的.链4@(5,5)的BM值是374 cm-1,表明碳链内嵌CNT管在一定程度上会影响到纳米管的BM值.对SWNT (2,2)的BM计算值为787 cm-1,比较接近由方程(2)得到的估算值796 cm-1;对于双壁碳纳米管DWNT(2,2)@(7,7)的振动分析显示,WNT(2,2)的BM值为787 cm-1,与SWNT(2,2)的BM计算值相等,这表明外层纳米管对内层纳米管的BM频率影响很小.
对于所有的n而言,线性链都具有一个对称中心,所有的拉曼活性模式是完全对称的.弯曲振动模式的频率很低:50~500 cm-1,因而可把注意力主要集中在Σg的伸缩振动模式上.在这种振动模式下,相邻碳原子做离开原位的振动,振动频率依赖于链中碳原子数的多少(偶数).采用“全电子高斯基组DF方法”做计算,可得到独立碳链Cn(n=2~20)的振动频率.当碳原子数n增加时,伸缩振动频率增大,一直持续到n=6时,频率达到最大值.在这之后随n增加,频率又将减小.采用类似的方法计算CNT(5,5)管中碳链和游离碳链的振动频率,其值与实验值基本吻合.且前者比后者约低60~90 cm-1.
用内嵌碳链的多壁碳纳米管进行拉曼散射实验时,于1 850 cm-1附近出现一个明显的吸收峰, HRTEM影像表明这条碳链大约有20 nm长;分析表明这条链包含一段较短的、被空位隔开的“片断”.正是这一 “片断”导致拉曼光谱中1 850 cm-1处的强吸收.链4@(5,5)中的伸缩振动频率为1 954 cm-1,链4@(6,6)的这种频率值增加到1 998 cm-1,但链4@(7,7)的这种频率却又降到1 993 cm-1.这些结果表明内嵌到较大的CNT管中,碳链的振动频率会增大,将趋于约2 000 cm-1这个值.
有关碳环、石墨片、碳笼、和碳管的振动频率计算表明,在片20@(7,7)中相互连接的环其伸缩振动频率具有最大值2 155 cm-1.在远离中心位置情况下,有关片20@(5,5)和片20@(7,7)的计算表明,石墨片的所有振动频率都低于1 645 cm-1.碳笼内嵌到CNT(7,7)管中具有的振动频率不会高于1 450 cm-1;且CNT(7,7)管中的CNT(2,2)的振动频率最高值为1 600 cm-1.
3结论
针对单壁扶手椅纳米管里内嵌碳链、碳环、石墨片、碳碗、碳笼和碳管等多种碳分子形成的复合结构,在能量、几何构型和振动频率等方面进行密度泛函计算;计算范围包括扶手椅纳米管(n,n),n=4~7,对应直径范围在0.553~0.953 nm之间.结果表明①直径等于或大于0.7 nm以上的碳纳米管能容纳线性碳链;②直径大于1.0 nm的碳纳米管还能与碳环、石墨片、碳笼或更小的纳米管形成内嵌式的结合;③具有悬空键的碳分子能与CNT管壁结合或形成其他稳定结构,这种情况是否出现取决于内嵌碳分子与纳米管壁间的间隔;④对于具有饱和键的碳分子而言,离开CNT壁的最小间隔约为0.34 nm,接近石墨夹层间隔;⑤较大的碳分子能引起CNT管壁局部变形甚至长程变形.
碳链和碳环的伸缩振动模式频率在1 800 cm-1以上,石墨片的伸缩振动频率为1 645 cm-1以下,而碳笼的伸缩振动频率最大值仅为1 450 cm-1.碳链的伸缩模式频率在嵌入CNT管时会减小,因此在1 850 cm-1处观察到的拉曼峰可能是由于碳链引起的,因为碳环太大以致于不能嵌入CNT(5,5)内形成稳定的复合结构.独立的碳环,如C18缩合C20在2 100 cm-1附近具有拉曼活性模式,但在1 700~2 000 cm-1范围内却没有.近来Ravagnan等人利用沉积有无定形碳的胶片在2 100 cm-1附近确定了碳链的一个拉曼峰,已经发现这个频率也出现在碳环的振动上.与在CNT管里封闭的几何构型相比,这个频率更有可能出现在胶片上.从计算结果还可以看到,独立的碳环比独立的碳链(n>10)更稳定.此外,计算结果还表明了碳纳米线(CNW’s)的存在,近年来的实验也观察到了多壁纳米管(MWNT’s)中稳定的CNW’s.这暗示着在多壁纳米管(MWNT)里嵌入更小纳米管且能够稳定的是直径为0.3 nm的最小纳米管CNT(2,2).
参考文献:
[1] LU J, NAGASE S, ZHANG S, et al. Strongly size-dependent electronic properties in C60-encapsulated zigzag nanotubes and lower size limit of carbon nanopeapods[J]. Physical Review B, 2003,68(12).
[2] OKADA S, OTANI M, OSHIYAMA A. Electron-state control of carbon nanotubes by space and encapsulated fullerenes[J]. Physical Review B, 2003,67(20):920-925.
[3] LIU Y, JONES R O, ZHAO X, et al. Carbon species confined inside carbon nanotubes: a density functional study[J]. Physical Review B, 2003,68(12).
[4] OKADA S, SAITO S, OSHIYAMA A. Energetics and electronic structures of encapsulated C60 in a carbon nanotube[J]. Physical Review Letters, 2001,86(17):3835-3838.
[5] MELLE-FRANCO M, KUZMANY H, ZERBETTO F. Mechanical interactions in all-carbon peapods[J]. Journal of Physical Chemistry B, 2003,107(29):6986-6990.
[6] 高鹭远. C-(60)@(n,0)与C-(20)@(n,n)的组装与性质----纳米豆子荚的量子化学计算与研究[J]. 沈阳大学学报(自然科学版), 2013,24(6):34-37.
(GAO L Y. Theoretical research for encapsulation of various carbon molecules in carbon nanotubes:Analysis to some calculations results of density functional[J]. Journal of Shenyang University(Natural Science), 2013,24(6):34-37.)
【责任编辑: 祝颖】
Some Calculations Results of Density Functional on Encapsulation of Various Carbon Molecules in Carbon Nanotubes
GaoLuyuan
(Normal School, Shenyang University, Shenyang 110003, China)
Abstract:A new type of carbon nanostructure formed by encapsulating the carbon chains, rings, graphitic sheets, bowls, cages, and tubes into single-walled nanotubes (CNT’s) is studied, with quantum chemistry method. Pseudopotential plane-wave basis is employed to optimize geometrical structure, and PBE of density functional theory is used to calculate the electron properties including energy, band structure, density of states, electron-phonon coupling parameter and vibration frequencies.
Key words:carbon chains; carbon rings; carbon bowls; carbon cages; graphitic sheets; carbon nanotubes
中图分类号:O 621.13; TB 383
文献标志码:A
文章编号:2095-5456(2016)01-0006-05
作者简介:高鹭远(1961-),男,辽宁沈阳人,沈阳大学副教授.
收稿日期:2015-07-30

