铜氧面电阻率温度线性依赖与空穴声子散射

毛 善 成

(淮阴工学院 图书馆, 江苏 淮安　223003)



毛 善 成

(淮阴工学院 图书馆, 江苏 淮安223003)

摘要:在BCS理论框架中,推导出高温铜氧化物材料中电子或空穴对间的电声作用强度T与电子费米速度成正比,与相互作用距离的平方根成反比关系,代入索末菲量子自由电子气模型的电阻率公式,计算出高温超导铜氧化物材料正常态电阻率ρab对温度成线性依赖的比例系数β≈ 0.4×10-6(Ω·cm·K-1),与经验结果较为一致.并用空穴-声子散射机制解释了空穴型高温超导铜氧化物正常态的电阻率随温度的线性依赖行为.

关键词:铜氧化物正常态; 高温超导体; 反常电阻率; 空穴-声子散射; 高温超导机理; 状态方程; 临界热动量

高温超导材料的正常态输运性质很反常,自铜氧化物高温超导体发现以来,人们利用多种实验手段对其反常的正常态性质进行了大量研究.然而到目前为止,对其反常的电阻率和霍尔系数等基本性质和高温超导机理问题的理解还没有形成统一的认识.Laughlin认为,这个凝聚态物理学最大的谜题能够从金属的传统理论开始解释[1-3].人们发现在高温超导材料中作为结构主体的Cu-O平面内正常态电阻率对温度有线性依赖,其电阻率ρ在很宽的温度范围内有线性的温度关系,如La2-xSrxCuO4的线性关系可从Tc附近40 K 延伸到1 100 K,而沿c轴方向电阻率大多数实验结果是半导体型温度行为.高温超导材料Cu-O面正常态电阻率ρab对温度成线性依赖可用式(1)表示:

(1)

对不同系列的高温超导材料,此种线性行为又非常相似,即对高质量的样品ρ0≈ 0,比例系数β≈ (0.4～0.5)×10-6(Ω·cm·K-1)[4-6].虽然,安德森[7]共振价键态(RVB)模型解释高温超导材料的相图方面并不成功,但安德森利用RVB模型计算出β≈10-6(Ω·cm·K-1),说明利用RVB模型解释高-Tc材料正常态线性电阻率的反常行为具有可行性.人们通常使用经典自由电子气理论和索末菲量子自由电子气模型解释欧姆定律,尤其是利用量子自由电子气模型说明材料电导率的本质更有利于理解费米面的重要性.由于超导电性发生在材料的费米面上,所以利用量子自由电子气模型来解释高-Tc材料正常态线性电阻率的反常行为就显得特别重要,对高-Tc材料的超导机理研究也具有一定的科学意义.

1理论模型

高温超导陶瓷材料是极性晶体,其母体是反铁磁绝缘体,掺杂使其变为坏金属成不良导体,在液氮温区能产生超导,故称高温超导体.掺杂改变材料的电子态结构,使费米面上的电子分为高能态电子和低能态费米电子(低能电子),其特点是高能态电子的速率强烈地依赖掺杂浓度,在极欠掺杂时,高能电子的速度达最大值并随掺杂量的进一步增加而线性下降;而低能费米电子的速率不随掺杂量增加而变化[8].文献[9]对文献[8]的工作进行了进一步处理,测量出高能电子费米速度随掺杂量的变化曲线(图1).

文献[9]假定高能电子和低能费米电子与晶格相互作用时存在竞争关系并产生快电子效应,利用慢电子在极性晶体中的运动规律模型[10]推导出赝隙态和超导态方程[9]458,如式(2)为赝隙态状态方程,式(3)为超导态状态方程.

(2)

(3)

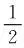
(4)

T为系统的热力学温度,可作为正常态电声作用强度;vC为正常态电子的费米速度;ξ为电子间相互作用距离,类似于库柏电子对的相干长度.

图1　掺杂量对高能费米电子速度的影响

2计算结果与讨论

2.1计算ab平面内电阻率

(5)

将各种参数[12]:n =1021cm-3=1027m-3,e=1.6×10-19C,u=103ms-1, lF≈ ξ ≈ ξ0=10-9m,α=5,m*=5me=5×9.1×10-31kg,代入β的计算公式,得β=0.4×10-6,和经验值 (0.4～0.5)×10-6Ω·cm·K-1基本一致.如果,电子密度n的取值再小一些,β的计算值就会增大些.有些测量结果偏高,如GdBa2Cu3O7-δ单晶样品在ab平面上电阻一温度关系的测量值[13]β=5.12×10-6`Ω·cm·K-1.

对于传统金属超导体,其电阻率随温度降低而成指数下降,到临界温度时,电阻率会突然下降到0,如图2中的A线.对高温超导体来说,电阻率随温度下降而降低,当系统进入赝隙态时,赝隙温度打开,电阻率变化会有突然下降现象如图2中B(T*-TC)曲线,但不会突然变化到0.系统继续降低温度到超导转变临界温度TC时系统的电阻率会突然下降到0.利用式(5)的比例系数β随正常态电子浓度的变化也能直观讨论0电阻现象.当正常态电子浓度下降时,β就会增大.当赝隙打开时,高能电子成为赝隙对,正常电子的浓度成指数下降,所以β增大曲线上翻.当超导能隙打开时,正常态电子浓度n →0,β→∞,电阻率线垂直于温度线,如图2(文献[14]).

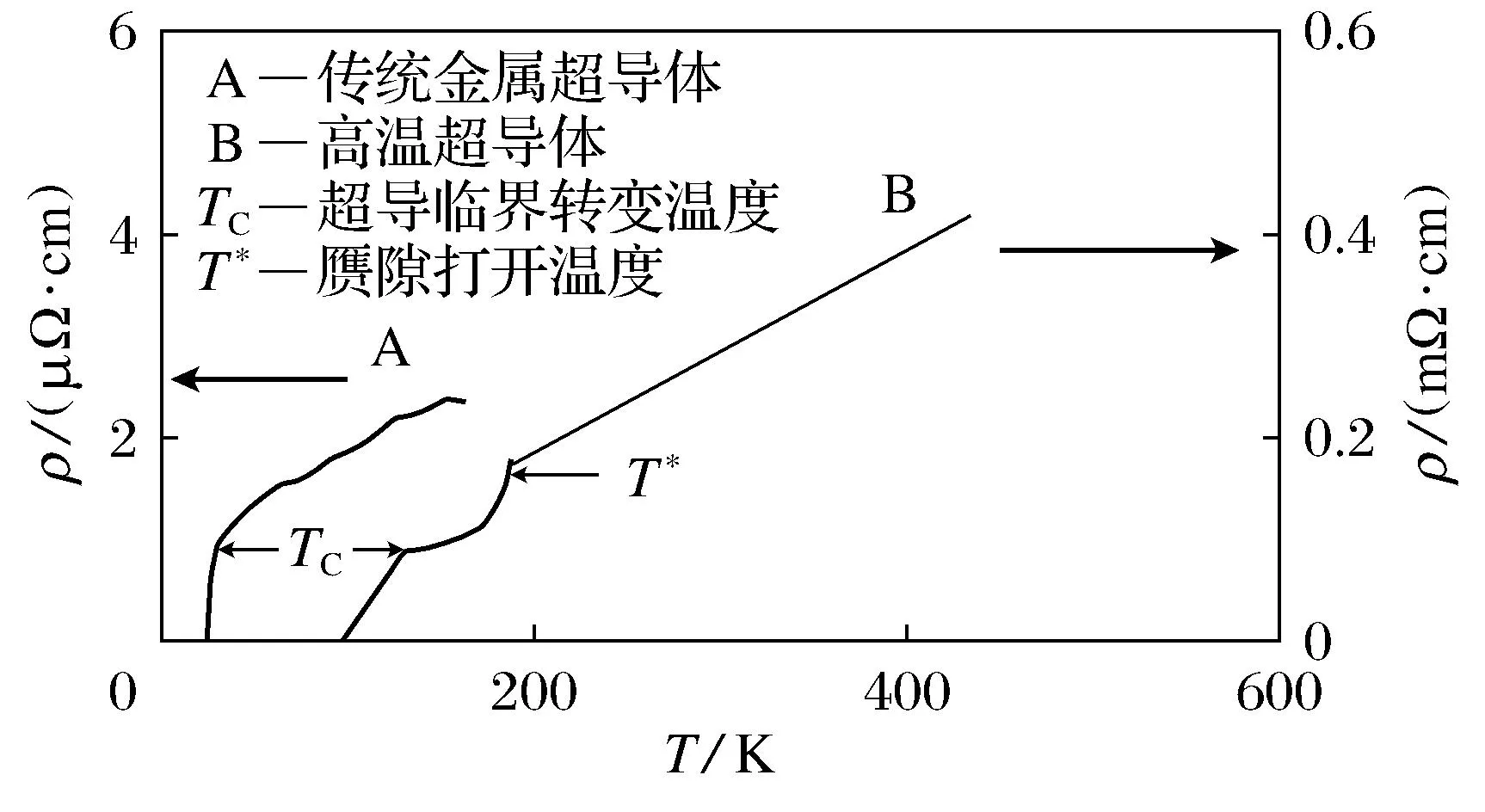
图2　电阻率随温度变化的示意图

2.2RVB模型对Cu-O面线性电阻率的解释

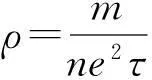
如果决定电阻率的弛豫时间按

2.3电-声散射在高Tc材料中的特殊意义

传统金属材料电子的费米速度约为106m·s-1,高Tc材料电子的费米速度约为105m·s-1,电子的热动量为κBT/vC(忽略电子的有效质量),可见高Tc材料电子的热动量比较高,约为传统金属的10倍.超导发生于动量空间的凝结,如何降低系统电子的热动量已成为关键问题.传统金属通过降温来降低电子的热动量,其超导临界转变温度都很低.高温超导的Tc值可达130 K以上,高压下超过160 K.通过比较可以看出,BCS机制只有在电子的热动量很小的情况下起决定性作用,使库柏对的动量变为0,而实现超导.传统金属材料通过降温使电子的热动量下降到BCS机制发生作用的临界值p,可用公式p=κBT/vF估算,其中vF≈106m·s-1,T≈40 K为McMillanTc极限值.估计p的最大值pmax≈ 5.5×10-28kg·m·s-1. 对于金属而言,金属铌的Tc=9.6 K,是金属中超导转变温度的最高记录,所以,绝大部分金属单质的临界值p还不足pmax的1/4.说明只有当电子的热动量p下降到pmax以下时BCS机制才能发生作用,实现超导.

高温铜氧化物超导材料中电子的费米速度约为105m/s,其电子的热动量要比传统金属的大10倍左右.可以通过电声散射(见式5)和适当降温使电子的热动量下降到BCS机制发生作用的临界值pmax以下.高温铜氧化物超导材料中电子分为高能费米电子和低能费米电子,作为比较,高能费米电子的热动量比低能费米电子的热动量要小,所以高能电子可以在较高的温度下发生电-声配对[17-19],形成赝隙态,但不发生超导.从图2看,系统进入赝隙态时,电阻率变化有突然下降的趋势,表现为曲线上翻但不会下降到0,所以没有超导现象出现.因为,系统进入赝隙态后,系统中仍有大量的低能费米电子处于正常态,其热动量大于pmax,BCS机制还不能发挥配对作用.只有进一步降温到低能费米电子的热动量小于pmax时BCS机制才能发挥配对作用实现超导.所以,高Tc超导材料的T*≥Tc.

2.4高温铜氧化物超导与电声散射

高温超导铜氧化物材料的超导机理虽然没有形成共识,但近年来电声作用(BCS)机理受到特别多的关注[20-23].正如Laughlin所说“这个凝聚态物理学最大的谜题能够从金属的传统理论开始解释”.文献[9]和本文的工作主要通过电声机制来解释高Tc材料超导电性的反常特性,提出BCS超导发生机制的必要条件是电子的热动量必须下降到临界值(pmax≈5.5×10-28kg·m·s-1)以下.如何让导电材料费米电子的热动量下降到临界值以下呢,到目前为止,有两种机制,一是传统的降温机制,另一是电声散射机制.在高温超导体中,两种机制都有,但电声散射是其主要的物理机制,这正是高温超导现象的复杂性所在.用BCS机制阐明高温超导现象首先遇到一个常识问题是McMillanTc( ≤40K)极限.如果通过电声散射使费米电子的热动量在较高的温度达到临界值以下,就可以在40K以上实现超导.其次,欠掺杂区高温超导的能隙与温度比值(2Δ0/κBTc)不服从BCS理论的计算结果,笔者用电声(BCS)机制进行了试探性解释(详见文献[9]).文献[9]的工作通过“电子热动量被晶格振动所吸收的假设”推导出赝隙的状态方程式(2)和超导态方程式(3),显然,正常态的状况方程式(4)也是基于上述假设推导的.从数学形式上看,三种状态有着共同的起源----电子与晶格之间的相互作用.说明高温铜氧化物超导材料的正常态已经有赝隙对和超导对形成的物理条件并包含着电声(BCS)机制的合理内核,这是对高温铜氧化物材料内在特征和三种状态(正常态、赝隙态和超导态)的整体认识.

2.5估算高温铜氧化物超导体的Tc极限

考虑临界热动量问题时,人们自然要问高Tc材料的热动量本征值很高,是传统材料的10倍,为何有高Tc值？因为高Tc材料对电子热动量的吸收能力强.将超导态状态方程式(3)变为式(6),可计算不同材料对电子热动量的吸收程度.

(6)

如不考虑电子的有效质量,α=1. 传统材料的相干长度ξ0≈10-6m,计算出p=4.4×10-28≈ 5.5×10-28kg·m·s-1. 说明传统材料吸收电子的热动量和其临界值 (pmax) 基本一致.高Tc材料的相干长度ξ0≈10-9m,所以高Tc材料吸收电子热动量为p=1.4×10-26kg·m·s-1,约为传统材料的30倍,如果考虑高Tc材料的电子热动量约为传统材料的10倍,那么,高温超导铜氧化物材料Tc极限值应为传统材料McMillanTc极限值的3倍,约120 K.1993年Schilling等[24]报告了Hg系超导体Tc值达135 K,几乎同时Gao等[25]在高压(45 GPa≈45万大气压)下实现164 K的超导记录,20年过去了,无人打破常态下高Tc≈135 K记录.利用Homes定律[26]和电声散射机制也可以估算高Tc的极限值.Homes等给出高Tc材料正常态电子的Planck量子耗散的特征时间[27]τ=ћ/(κBTc),再短的时间将被禁止.如果高Tc铜氧化物材料的超导机理为BCS机制,那么τ≈ξ0/u,当ξ0→d(d是一个晶格长度,约10-10m)时,τ有极小值,所以不等式(7)成立.

(7)

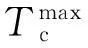
Homes定律表明高温铜氧化物材料具有很高的超导转变温度,是由于其正常态电子是极度耗散的[27]512,其正常态电子具有极大的热动量,已经达到了电声机制的极限,如对式(4)作类似于式(6)的变换,可得κBT/vc=kκB(u/ξ)(1/α).当ξ→d,电子的热动量最大,再大的热动量将会被禁止.近年来,在研究高温超导机理方面,共振价键态理论开始复苏,和电声机制一样受到更多关注,这是巧合还是必然？在这里,本文给出的答案是RVB态是电声(BCS)机制的极限状态.电子或空穴对间的作用距离为一个晶格长度也就是共价键的键长时,电子对就成为共价电子对.如果共价电子对通过空穴-声子散射机制形成电阻率,也能与温度成线性依赖.此时,ξ=d=10-10m时,式(5)计算出的β≈1.2×10-6Ω·cm·K-1,和Anderson的RVB模型的计算值比较一致.

3结论

高温超导材料是一种极性晶体,掺杂使其具有低的载流子密度,使其高能电子的费米速度进一步增加,而低能电子的费米速度不受影响;同时,载流子的费米速度只有传统材料的十分之一,可以利用慢电子在极性晶体中的运动规律推导其物理运动规律和模型.高能费米电子的成对运动是解释膺隙形成以及温度随掺杂量变化的物理基础,低能费米电子的成对运动是解释能隙和温度T的比值随掺杂量的变化等反常行为的物理基础[9]458.在正常态,其载流子的成对运动也是其电阻率对温度线性依赖的物理基础.尽管,高温超导机理还没有定论,但在赝隙态有赝隙对、超导态有库柏对存在已经被很多实验[31]所证实并被广泛接受.考虑到正常态载流子的成对运动行为在大的温区(10～1 000 K)范围成立,再加上本文的电声模型对正常态电阻率的计算结果与实验测量值较为一致,所以,该研究推断载流子成对的物理机制为“空穴-声子散射(holon-phonon)”,进一步推论:低温下,空穴-声子散射表现为吸引力,如赝隙的形成,更低的温度条件下形成超导隙,而高温情况下空穴-声子散射表现为排斥力(共振价键态).

参考文献:

[1] 张章. 高温超导起源基本假设引发巨大争论[N/OL]. 中国科学报, 2013-12-31(3). http:∥news.sciencenet.cn/htmlnews/2013/12/286944.shtm?id=286944

(ZHANG Z. The basic assumptions of origin of HTS triggered a huge controversy[N/OL]. China Science Daily, 2013-12-31(3). http:∥news.sciencenet.cn/htmlnews/2013/12/286944.shtm?id=286944.)

[2] LAUGHLIN R B. Hartree-Fock computation of the high-Tccuprate phase diagram[J]. Physical Review B, 2013,89(3):407-411.

[3] LAUGHLIN R B. Fermi-liquid computation of the phase diagram of high-Tccuprate superconductors with an orbital antiferromagnetic pseudogap[J]. Physical Review Letters, 2014,112(1):017004-017007.

[4] 阎守胜. 高温氧化物超导材料奇特的输运性质[J]. 物理, 1992,21(7):391-393.

(YAN S S. Abnormal transport property of high temperature oxide supercoaductors [J].Physics, 1992,21(7):391-393.)

[5] 阎守胜. 固体物理学[M]. 北京:北京大学出版社, 2000:479.

(YAN S S. Fundamentals of solid state physics[M]. Beijing: Peking University Press, 2000:479.)

[6] BERTRAM B. Physical properties of high-Tcsuperconductors[J]. Physics Today, 1991,44(6):44-50.

[7] ANDERSON P W, ZOU Z. Normal tunneling and normal transport-diagnostics for the resonating-valence-bond state[J]. Physical Review Letters, 1988,60(1):132-135.

[8] ZHOU X J, YOSHIDA T, LANZARA A, et al. High-temperature superconductors universal nodal Fermi velocity[J]. Nature, 2003,423(6938):398.

[9] 毛善成. 电-声机制致高温超导特性随掺杂量演变[J]. 沈阳大学学报(自然科学版), 2014,26(6):457-461.

(MAO S C. Electron-phonon coupling leading to high-temperature superconductivity with doping content evolution[J]. Journal of Shenyang University(Natural Science, 2014,26(6):457-461.)

[10] LEE D, LOW F E,PINES D. The motion of slow electrons in a polar crystal[J]. Physical Review, 1953,90(4):297-302.

[11] 曹全喜. 固体物理基础[M]. 西安:西安电子科技大学出版社, 2008:173.

(CAO Q X. Fundamentals of solid state physics[M]. Xi’an: Xidian University Press, 2008:173.)

[12] SAXENA A K. High-temperature superconductors[M]. Berlin: Springer, 2012:58.

[13] 方明虎,夏健生,许祝安,等. GdBa2Cu3O7-δ单晶的各向异性研究[J]. 物理学报, 1989,38(2):313-316.

(FANG M H, XIA J S, XU Z A. Studies on anisotropy for single-crystal GaBa2Cu3O7-δ[J]. Acta Physica Sinica, 1989,38(2):313-316.)

[14] 韩汝珊. 高温超导物理[M]. 北京:北京大学出版社, 2002:228-229.

(HAN R S. Physics of high temperature super-conductivity[M]. Beijing: Peking University Press, 2002:228-229.)

[15] XING D Y,LAI W Y,SU W P, et. al. Theory of resistivity for charged bosons in high-Tcoxides compounds[J]. Solid State Communication, 1988, 65(11):1319-1321.

[16] 刘楣,邢定钰. 共振价键模型中正常态电阻率的讨论[J]. 物理学报, 1990,39(9):1453-1460.

(LIU M, XING D Y. Discussion on normal state resistivity in RVB system[J]. Acta Physica Sinica, 1990,39(9):1453-1460.)

[17] RENNER C, REVAZ B, GENOUD J Y,et al. Pseudogap precursor of the superconducting gap in underdoped and overdoped Bi2Sr2CaCu2O8+δ[J].Physical Review Letters, 1998,80(1):149-152.

[18] RENNER C, REVAZ B, KADOWAKI K, et al. Observation of the low temperature pseudogap in the vortex cores of Bi2Sr2CaCu2O8+δ[J]. Physical Review Letters, 1998,80(8):3606-3609.

[19] KUGLER M, RENNER C, ONO S, et al. Scanning tunneling spectroscopy of Bi2Sr2CuO6+δ: New evidence for the common origin of the pseudogap and superconductivity [J]. Physical Review Letters, 2001,86(21):4911-4914.

[20] LANZARA A, BOGDANOV P V, ZHOU X J, et al. Evidence for ubiquitous strong electron-phonon coupling in high-temperature superconductors[J]. Nature, 2001,412(6846):510-514.

[21] LOZANNE A. Superconductivity:Hot vibes[J]. Nature,2006, 442(7102):522-523.

[22] JINHO L, FUJITA K, MCELROY K, et al. Interplay of electron-lattice interactions and superconductivity in Bi2Sr2CaCu2O8+δ[J]. Nature, 2006,442(7102):546-550.

[23] CHEN X J, VIKTOR V S,WU Z G, et al. Unified picture of the oxygen isotope effect in cuprate superconductors[J]. Proceedings of the National Academy of Sciences, 2007,104(10):3732-3735.

[24] SCHILLING A , CANTONI M , GUO J D, et al. Superconductivity above 130 K in the Hg-Ba-Ca-Cu-O system [J]. Nature, 1993,363(6424):56-58.

[25] GAO L, XUE Y Y , CHEN F, et al. Superconductivity up to 164 K in HgBa2Cam-1CumO2m+2+δ(m=1, 2, and 3) under quasihydrostatic pressures[J]. Physical Review B, 1994,50(29):4260-4263.

[26] HOMES C C, DORDEVIC S V, STRONGIN M et al. A universal scaling relation in high temperature superconductors [J]. Nature, 2004,430(6999):539-541.

[27] ZAANEN J. Superconductivity: Why the temperature is high[J]. Nature, 2004,430(6999):512-513.

[28] SRINIVASAN R , RAMACHANDRAN V , SESHADRI A T, et al. Anomalous behaviour of sound velocity in the highTcsuperconductor YBa2Cu307[J]. Pramana, 1987,29( 6):603-609.

[29] DROZDOV A P, EREMETS M I, TROYAN I A. Conventional superconductivity at 190 K at high pressures[R]. Eprint Arxiv, 2014.

[30] 韩汝珊. 铜氧化物高温超导电性实验与理论研究[C]∥郭卫. 高温超导:从反铁磁到共振价键态—Kramers超交换机制. 北京:科学出版社, 2009:348.

(HAN R S. Superconductivity experiment and theory of high temperature superconducting cuprate[C]∥GUO W. High temperature superconductivity: from anti-ferromagnet to RVB state: Kramers exchange mechanism . Beijing: Science Press, 2009:348.)

[31] GOUGH C E, COLCLONG M S, FORGAN E M, et al. Flux quantization in a High-Tcsuperconductor[J] . Nature , 1987,326(6116):855.

【责任编辑: 祝颖】

Linear Dependence of Resistivity-Temperature and Holon-Phonon Scattering in Cu-O Planes

MaoShancheng

(Library, Huaiyin Institute of Technology, Huai’an 223003, China)

Abstract:Within BCS theoretical framework, it derives that the electron-phonon coupling intensity T (temperature) in two electrons or holons in high-Tc materials, which is proportional to velocity of electrons and inverse to the square root of interaction length in two electrons or holons. It is computed that the proportional coefficient ( 0.4×10-6) of the resistivity linear rise with temperature by Sommarfold’s free-electron gas model, the computed result in accordance with empirical values β≈ (0.4 ～0.5)×10-6(Ω·cm·K-1). The linear dependence behaviour of resistivity variation with temperature is explained by holon-phonon scattering.

Key words:normal states of copper oxides materials; high temperature superconductor; abnormal resistivity; holon-phonon scattering; high-Tc superconducting mechanism; states equations; critical heat momentum

中图分类号:O 511

文献标志码:A

文章编号:2095-5456(2016)01-0001-05

作者简介:毛善成(1960-),男,江苏沭阳人,淮阴工学院图书馆副教授,博士.

收稿日期:2015-09-28