改进的加权支持向量机回归的谐波发射水平估计方法
邱思语 杨洪耕
(四川大学电气信息学院 成都 610065)
改进的加权支持向量机回归的谐波发射水平估计方法
邱思语杨洪耕
(四川大学电气信息学院成都610065)
摘要提出一种利用改进的加权支持向量机回归估计系统谐波阻抗及谐波发射水平的新方法。根据公共连接点处谐波测量数据的差异,利用欧几里德距离作为加权指标修正支持向量机的误差要求,通过线性插值确定惩罚参数的加权参数,以此形成用于估计系统谐波阻抗的加权支持向量机回归模型,从而求解谐波发射水平。通过对仿真电路的理论分析和现场数据的实际应用,证明了所提方法能有效抑制背景谐波波动对估计结果的影响。
关键词:谐波阻抗谐波发射水平加权支持向量机回归
Assessment Method of Harmonic Emission Level Based on the Improved Weighted Support Vector Machine Regression
QiuSiyuYangHonggeng
(School of Electrical Engineering & InformationSichuan UniversityChengdu610065China)
AbstractThis paper proposes a new method to estimate the system harmonic impedance and the harmonic emission level based on the improved weighted support vector machine (WSVM) regression.According to the differences of harmonic measurement data at the point of common coupling,the WSVM can be obtained by correcting the error requirement of SVM by using Euclidean distance as a weighted index and determining the weighted coefficient of the penalty parameter by linear interpolation.Then the system harmonic impedance and the harmonic emission level can be calculated.Based on analyzing the simulation of the circuit and the practical application of field data,it proves that the proposed method can effectively restrain the influences caused by the fluctuation of the background harmonics on the estimation results.
Keywords:Harmonic impedance,harmonic emission level,weighted,support vector machine,regression
0引言
当今电网在飞速发展的同时,也带来了许多急需解决的问题。其中,大规模的非线性和冲击性负荷在接入电网后产生了严重的电力谐波污染问题。准确地估计用户侧和系统侧的谐波发射水平对PCC点(公共连接点)的谐波污染责任分割起着至关重要的作用[1-6]。而评估谐波发射水平的难点在于如何在系统参数和电网运行方式不断变化的情况下准确地估计系统谐波阻抗[7-13]。
系统谐波阻抗估计方法主要分为“干预式”和“非干预式”两类。“干预式”方法利用向电网注入谐波/间谐波电流或者某条支路的开断来估计谐波阻抗,这种外界的干预可能影响电力系统的正常运行状态,不能广泛使用。“非干预式”方法则是围绕可测得的PCC点谐波数据进行研究,从已知数据中挖掘和提取谐波阻抗信息,主要包括:①波动量法[1],考虑背景谐波波动较小时系统谐波阻抗可近似由PCC点谐波电压和电流波动量的比值代替,简单实用,因此被广泛应用。但该方法要求测量参数具有较高的准确性且背景谐波基本保持稳定;②回归法[8-10],根据电力系统等效电路推导出回归方程,并将回归方程中的截距项视作恒定,从而将谐波阻抗的求解转换为回归系数的求解,但该方法也要求背景谐波基本保持稳定以满足回归假设,否则回归方程将失去原有的稳健性;③随机独立矢量法[11],考虑实际电网中PCC点谐波电流受背景谐波影响较小,以独立随机矢量协方差为零的思想建立模型,推导出谐波阻抗的估计公式,在一定程度上削弱了背景谐波波动的干扰,但其要求谐波电流的波动由用户侧主导,谐波电压的波动由双方共同主导,当系统波动不符合上述要求时,该方法计算结果值得进一步商榷;④支持向量机法[13],通过结构风险最小化原理提高泛化能力,较好地解决了小样本、非线性、高维数、局部极小点等实际问题,已在模式识别、信号处理和函数逼近等领域得到了应用。文献[13]以PCC点谐波数据作为输入,利用支持向量回归机回归估计谐波阻抗,由于二次规划的解是全局最优且惟一的,因此该方法具有较好的估计精度和泛化性,但该文中并未根据支持向量样本对训练结果的影响提出模糊隶属度,忽略了支持向量样本个体间的差异,即未考虑背景谐波波动造成的谐波测量数据的差异对阻抗估计结果的影响,估计结果可能偏离真实值。
基于现有支持向量机法计算系统侧谐波阻抗的不足,本文提出基于改进的加权支持向量机方法[17,18]的谐波阻抗估计方法,提出以权参数衡量谐波样本间的差异性,从而修正回归模型中的惩罚参数和误差要求,达到抑制背景谐波波动的效果。对理论进行仿真计算并通过现场数据验证,证明该方法能有效抑制背景谐波的影响。
1支持向量机法
电力系统谐波分析的等效电路模型如图1所示。其中,Is和Zs分别为系统侧某次谐波的等效电流源和谐波阻抗;Ic和Zc分别为用户侧某次谐波的等效电流源和谐波阻抗;UPCC和IPCC分别为PCC点的某次谐波电压和电流,为测量所得数据。
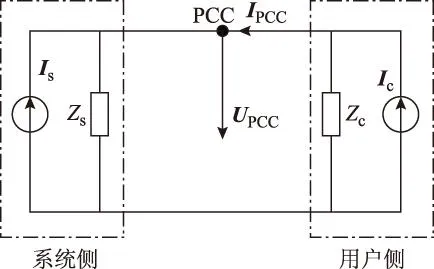
图1 系统侧和用户侧等效电路Fig.1 Norton equivalent of the utility and customer
根据电路原理,可推导出
UPCC=IPCCZs+IsZs
(1)
UPCC=-IPCCZc+IcZc
(2)
将式(1)、式(2)整理后可得
(3)
(4)

在采用支持向量机构造回归估计函数时,通常转换为构造并求解凸二次规划问题。
(5)
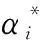
在上述二次规划问题中,误差要求ε和惩罚参数C的选取是影响支持向量机回归结果的关键。ε表示回归模型对训练样本误差的要求,ε值越小意味着对模型回归精度的要求越高,解得的回归函数精度也越高。惩罚参数C表示对超出误差要求ε的样本数据的惩罚,C值越小意味着对超出误差要求的样本惩罚力度就越小,从而增大训练误差[17,18]。在文献[13]采用的支持向量机方法中,回归模型需在一开始确定误差要求ε和惩罚参数C的值,且在之后的计算中保持不变,即对于所有的谐波数据,其误差要求及超出误差要求的惩罚一样。但实际在计算系统谐波阻抗时,考虑背景谐波波动的影响,不同时刻PCC点的谐波电压和谐波电流对估计谐波阻抗的重要性有所不同,受背景谐波波动影响越小的数据重要性越大,针对不同重要性的谐波样本应选择不同的误差要求和惩罚参数加以约束,从而减少重要性小的谐波数据对阻抗估计的影响。因此,本文提出采用改进的加权支持向量机回归[17,18]计算系统侧谐波阻抗。
2改进的加权支持向量机回归的谐波阻抗及谐波发射水平估计方法
2.1基本原理
在加权支持向量机中,首先应量化样本的重要性,然后以样本的重要性作为加权指标确定每个样本的误差要求ε和惩罚参数C的加权参数ti和si[17,18]。为了量化各样本数据的重要性,本文采用欧几里德距离作为量化指标,计算测试样本与各训练样本的距离,并按距离大小将训练样本重新排序。欧几里德距离越短,样本重要性越大,惩罚参数C的权参数si越大,误差要求ε的权参数ti越小。基于上述分析,最重要样本(距离最短样本)的权参数si应取最大值,ti应取最小值,故令si=1,ti=0.01;而最不重要样本(距离最远样本)的权参数si应取最小值,ti应取最大值,故令si=0.01,ti=1[17]。经多次实验验证,利用两种极端情况下的样本参数,通过线性插值计算其余样本的权参数[17]。
权参数ti和si确定后,原有的误差要求ε和惩罚参数C也相应地改变为εti和Csi,式(5)的凸二次规划问题即转换为
(6)
求解式(6)的凸二次规划问题即可得到拉格朗日乘子
(CRISPR)-Cas9是当下热门的基因编辑技术,但无法对细胞器中基因进行编辑。而PPR家族蛋白具备进入细胞器中与单链RNA结合的能力,并且识别结合RNA 4种核苷酸的部分PPR基序特点已被研究证实,还有更多的识别密码正在被研究和验证。在此基础上,针对靶标RNA单链序列特征,人工设计对应的PPR蛋白,通过融合相应的功能结构域,人工设计融合的PPR蛋白有望成为能够调控细胞器基因表达的新一代生物技术。
(7)
从而构造回归估计函数
(8)
(9)
(10)
2.2系统侧谐波阻抗及谐波发射水平估计


图2 加权支持向量机估计Zs步骤Fig.2 The steps of the Zs estimation by weighted support vector machine
回归得到谐波阻抗Zs后即可求解用户侧谐波电压发射水平
Uc-PCC=IPCCZs
(11)
从而可得到系统侧谐波电压发射水平
Us-PCC=IsZs=UPCC-Uc-PCC
(12)
3仿真实验
根据图1所示系统侧和用户侧等效电路,用Matlab按照文献[11]的仿真模型生成数据,等效电路的对应参数设计如下:
1)Ic幅值初始值为143.93 A,Ic的相角恒为0°,对Ic的幅值加上±20%的随机波动。
2)Is幅值初始值为Ic的k倍,其中k可取0.1、0.4、0.7、1.0、1.3、1.5,Is相角初始值为60°,对Is的幅值加上±5%的随机波动,对Is的相角加上20%的正弦波动。
4)Zs幅值初始值为0.101 76 Ω,加上20%正弦波动;Zs相角初始值为70°,加上10%正弦波动。
利用上述等效电路仿真模型随机生成10 000组样本数据,按每60组样本数据分段进行递推计算,利用本文方法(方法4)进行系统谐波阻抗及谐波发射水平的估计,同时与二元回归法[9](方法1)、支持向量机法[13](方法2)及独立随机矢量法[11](方法3)进行比对,结果见表1及表2。

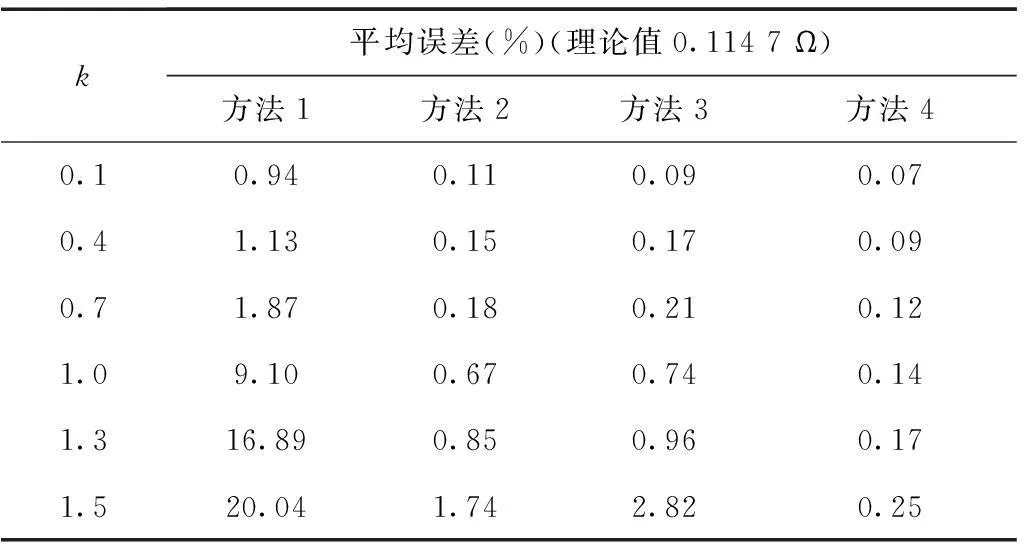
k平均误差(%)(理论值0.1147Ω)方法1方法2方法3方法40.10.940.110.090.070.41.130.150.170.090.71.870.180.210.121.09.100.670.740.141.316.890.850.960.171.520.041.742.820.25
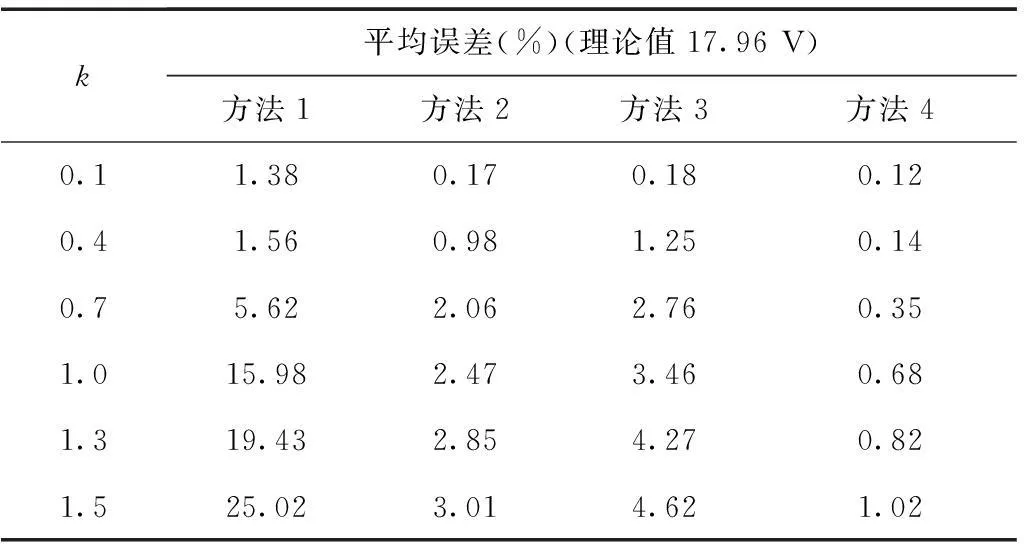
表2 Uc-PCC 95%概率值估计误差
k的取值代表不同的背景谐波波动情况,从表1、表2可看出,随着k值的增加,4种方法的计算误差均呈不同程度的增长趋势,而本文方法的计算误差增长趋势最小,随着k值的变化基本保持稳定,证明本文方法具有更好的计算稳定性。而在相同背景谐波波动情况下,本文方法的计算结果误差最小,最接近真实值,具有更高的计算精度。而在计算速度方面,不同的测试样本需要重新计算样本权参数,并重新进行训练,在训练样本数量不多时,计算速度与传统方法差异并不明显;而在训练样本数量巨大时,可以丢弃那些空间距离较远的训练样本,只保留数量较少的训练样本,以减少样本的训练时间。
4实测数据计算
本文采用现场实测数据进一步对所提方法的有效性和准确性进行验证。实际测量数据来自一100 MV·A的工业直流电弧炉的150 kV母线,系统短路容量为7 500 Mvar。测量数据由LEM TOPAS 1000系列电能分析仪以6 400 Hz的采样频率测得。图3为PCC点测得的某日连续10 h内的3次谐波电压和电流幅值。
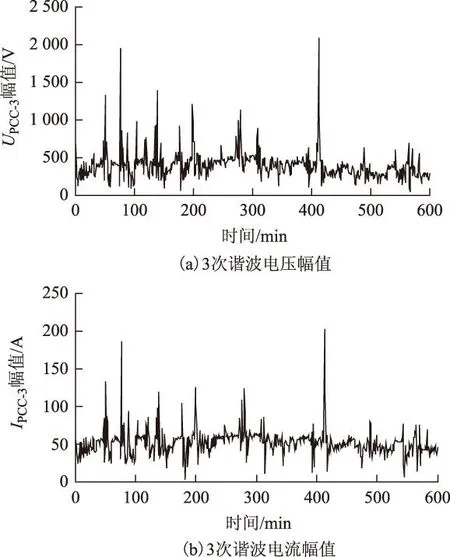
图3 PCC点3次谐波电压和电流幅值Fig.3 Magnitude waveforms of the 3rd harmonic voltage and current at the PCC
分别利用上述4种方法对实测3次谐波数据按60 min分段计算系统谐波阻抗,计算结果如图4所示。
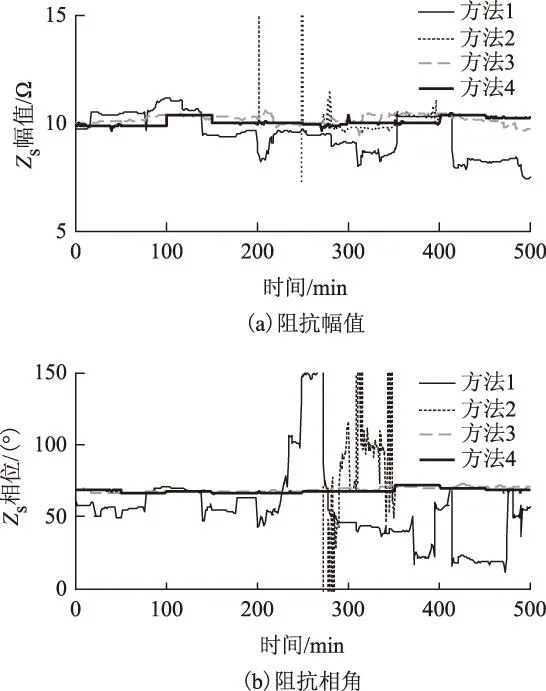
图4 系统3次谐波阻抗幅值和相角Fig.4 The 3rd harmonic impedance magnitudes and angles of Zs
分析图4可知,方法1(二元回归法)利用最小二乘法回归估计谐波阻抗,回归方程中的截距会随背景谐波波动而变化,从而使回归法失去原有的稳健性,导致阻抗估计结果波动较大;方法2(支持向量机法)利用支持向量机回归求解谐波阻抗,由于其解是全局最优且惟一的,具有较好的精度,但其未考虑背景谐波波动造成样本差异的问题,导致支持向量机的回归估计在局部偏离真实值;方法3(独立随机矢量法)利用PCC点谐波电流与背景谐波的弱相关性推导出谐波阻抗的估计公式,有效抑制了背景谐波波动的影响,估计结果较为平稳;方法4(本文方法)利用对误差要求和惩罚参数C加权的思想解决了方法2存在的问题,估计结果有明显改善,与方法3相比,估计结果更为平滑,且通过第3节仿真实验分析,能更好地抑制背景谐波波动的影响,具有更好的精度和稳定性。
最后,通过已求得的系统谐波阻抗计算PCC点用户侧和系统侧谐波电压发射水平,得到的发射水平95%概率值如表3所示。利用停机运行时的3次谐波电压作为系统侧谐波电压发射水平的真实值,如图5所示,并计算95%概率值为212.46 V。与表3数据相比,进一步验证了本文方法的准确性和有效性。
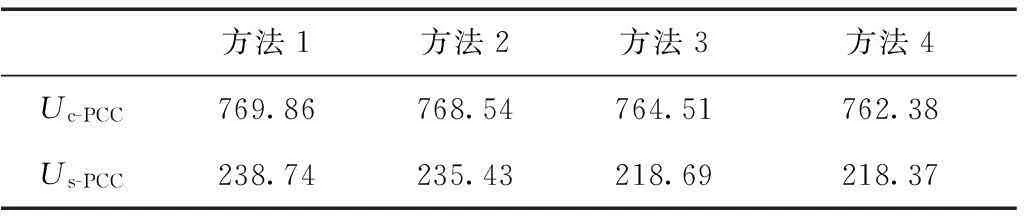
表3 用户侧和系统侧谐波电压发射水平95%概率值
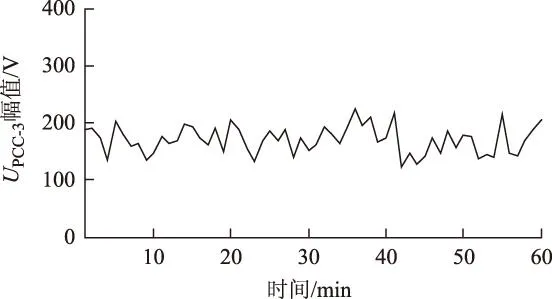
图5 停机1 h的3次谐波电压幅值Fig.5 The 3rd harmonic voltage amplitude in a shutdown hour
5结论
本文方法在计算系统谐波阻抗时,利用谐波测量数据的差异对支持向量机的误差要求和惩罚参数C加权,抑制了背景谐波波动对阻抗估计结果的影响。仿真电路的计算和现场实测数据的分析均证明了本文所提方法的准确性和有效性,具有很好的理论研究价值和工程应用前景。
在加权支持向量机中,每更换一次测试样本,样本权参数则需要重新计算,并重新进行训练,计算量大,计算速度慢。因此,这种加权支持向量机方法一般适用于离线计算或对实时性要求不高的场合。在样本数量巨大时,丢弃一些重要性指标较低的训练样本,可减少训练时间及训练计算量。
参考文献
[1]Yang H,Pirotte P,Robert A.Harmonic emission levels of industrial loads statistical assessment[C]//CIGRE Proceedings:International Council on Large Electric Systems,Paris,1996:456-462.
[2]Xu Wilsun,Liu Yilu.A method for determining customer and utility harmonic contribution at the point of common coupling[J].IEEE Transactions on Power Delivery,2000,15(2):804-811.
[3]Xu Wilsun,Ahmed E E,Zhang Xiqin,et al.Measurement of network harmonic impedances:practical implementation issues and their solutions[J].IEEE Transactions on Power Delivery,2002,17(1):201-216.
[4]林海雪.公用电网谐波国标中的几个问题[J].电网技术,2003,27(1):65-70.
Lin Haixue.Some problems in national standard for harmonics in public supply network[J].Power system Technology,2003,27(1):65-70.
[5]国家技术监督局.GB/T 14549—1993电能质量:公用电网谐波[S].北京:中国标准出版社,1993.
[6]刘秀玲,王洪瑞.电网谐波阻抗的测量及修正[J].电力系统及其自动化学报,2007,19(2):55-58.
Liu Xiuling,Wang Hongrui.Measurement and correction of network harmonic impedances[J].Proceedings of CSU-EPSA,2007,19(2):55-58.
[7]杨洪耕,王磊.基于拉盖尔多项式的非线性负荷谐波发射水平估计[J].中国电机工程学报,2005,25(7):81-85.
Yang Honggeng,Wang Lei.Assessing harmonic emission levels from non-loads using Laguerre polynomials[J].Proceedings of the CSEE,2005,25(7):81-85.
[8]车权,杨洪耕.基于稳健回归的谐波发射水平估计方法[J].中国电机工程学报,2004,24(4):39-42.
Che Quan,Yang Honggeng.Assessing the harmonic emission level based on robust regression method[J].Proceedings of the CSEE,2004,24(4):39-42.
[9]张巍,杨洪耕.基于二元线性回归的谐波发射水平估计方法[J].中国电机工程学报,2004,24(6):50-53.
Zhang Wei,Yang Honggeng.A method for assessing harmonic emission level based on binary linear regression[J].Proceedings of the CSEE,2004,24(6):50-53.
[10]李丽,马宏忠,姜宁,等.基于改进偏最小二乘法的系统谐波阻抗及谐波发射水平估算[J].电力系统保护与控制,2011,39(1):92-95,131.
Li Li,Ma Hongzhong,Jiang Ning,et al.Assessing harmonic impedance and the harmonic emission level based on improved partial least-squares regression method[J].Power System Protection and Control,2011,39(1):92-95,131.
[11]惠锦,杨洪耕,林顺富,等.基于独立随机矢量协方差特性的谐波发射水平评估方法[J].电力系统自动化,2009,33(7):27-31.
Hui Jin,Yang Honggeng,Lin Shunfu,et al.Assessment method of harmonic emission level based on covariance characteristic of random vectors[J].Automation of Electric Power Systems,2009,33(7):27-31.
[12]龚华麟,肖先勇,刘亚梅,等.基于主导波动量筛选原理的用户谐波发射水平估计方法[J].中国电机工程学报,2010,30(4):22-27.
Gong Hualin,Xiao Xianyong,Liu Yamei,et al.A method for assessing customer harmonic emission level based on the dominant fluctuation filtering principle[J].Proceedings of the CSEE,2010,30(4):22-27.
[13]康婕,解绍锋,刘晓菊,等.基于支持向量机的谐波阻抗估计方法[J].电力系统保护与控制,2010,38(22):131-134,205.
Kang Jie,Xie Shaofeng,Liu Xiaoju,et al.Assessing the harmonic impedance based on support vector machine[J].Power System Protection and Control,2010,38(22):131-134,205.
[14]Vapnik V N.The Nature of Statistical Learning Theory[M].New York:Springer,1995.
[15]阎满富,田英杰.改进的支持向量回归机[J].系统工程,2004,22(10):9-12.
Yan Manfu,Tian Yingjie.The improvement of support vector regression[J].Systems Engineering,2004,22(10):9-12.
[16]杜树新,吴铁军.用于回归估计的支持向量机方法[J].系统仿真学报,2003,15(11):1580-1586.
Du Shuxin,Wu Tiejun.Support vector machines for regression[J].Journal of System Simulation,2003,15(11):1580-1586.
[17]杜树新,吴铁军.回归型加权支持向量机方法及其应用[J].浙江大学学报(工学版),2004,38(3):47-51.
Du Shuxin,Wu Tiejun.Weighted support vector machines for regression and its application[J].Journal of Zhejiang University(Engineering Science),2004,38(3):47-51.
[18]李忠浩,王宇.改进的加权型支持向量回归方法[J].计算机辅助工程,2006,15(1):31-33.
Li Zhonghao,Wang Yu.Improved weighted support vector regression[J].Computer Aided Engineering,2006,15(1):31-33.
[19]邓乃扬,田英杰.支持向量机—理论、算法与拓展[M].北京:科学出版社,2009.
邱思语男,1990年生,硕士研究生,研究方向为电力系统谐波分析与评估。
E-mail:412582182@qq.com(通信作者)
杨洪耕男,1949年生,教授,博士生导师,研究方向为电能质量分析与控制。
E-mail:pqlab99@126.com
作者简介
中图分类号:TM72
收稿日期2015-03-27改稿日期2015-10-08

