关节型机器手臂笛卡尔轨迹规划

朱清智，张 毅

(河南工业职业技术学院，南阳473000)

关节型机器手臂笛卡尔轨迹规划

朱清智，张 毅

(河南工业职业技术学院，南阳473000)

为了消除机器手臂空间轨迹规划中采用一般插补法产生的尖角，且让机器手臂在非匀速运动状态下，能够具有连续的速度和加速度.结合空间直线插补和圆弧插补算法，提出一种新的圆弧连接均值直线插补法，并在此基础上进行二次插值，从而使得该算法在加速和减速时也可以获得很好的平滑性，在MATLAB环境下对算法进行了仿真.通过该算法以及对拟合度的调整可以获得最优规划路径.该算法在机器手臂轨迹规划当中具有较好的可行性.

二次插补;机器手臂;轨迹规划;MATLAB仿真

0 引言

机器手臂的轨迹规划是指通过对机器手臂各关节速度、加速度的控制，从而在空间上形成某一特定的运动轨迹.轨迹规划通常分为关节空间轨迹规划和笛卡尔空间轨迹规划两类.前者简单方便且不易出现特殊位形，却存在末端轨迹不直观的现象;而笛卡尔空间轨迹规划直观但容易出现特殊位形.

目前，学者们对关节空间的轨迹规划算法进行了大量的研究，对于简单的机器手臂轨迹规划，通常使用三次多项式和五次多项式进行插值［1］，该类算法具有计算量小，速度曲线连续的优点，但却存在明显的波动.Bazaz等［2］针对基于时间参量提出了三次样条在线轨迹规划，改善了轨迹规划的的时间，但是其加速度曲线却存在不连续现象;B样条曲线作为采用较为广泛的算法之一，其速度、加速度曲线连续，有很好的局部性特征，误差波动影响较小，但是其速度和加速度的起始值和终值不能同时为零.Miti等［3］通过对B样条曲线参数的优化，获得了在约束条件下的最优规划轨迹;此外，Sahar等［4］研究了一种基于时间的比例法，该算法验证是否能实现机器人规划的轨迹;Taylor［5］用四元素法对于轨迹规划算法的改进等.

相比之下，学者们对于笛卡尔空间的轨迹规划方面的研究则相对较少，目前被广泛使用和讨论的有空间直线插值算法和空间圆弧插值算法［6］等.当机器手臂的轨迹为几段连续的直线轨迹或连续的圆弧轨迹时都可能在连接处形成尖角，从而影响轨迹的平滑性.通常的做法是将靠近尖角处的连续直线或曲线进行分离，得到多段的曲线，然后对各段曲线进行单独规划.这样一来就增加了轨迹的平滑性，但电机在各段曲线间会不停地启动和停止，从而消耗过多的能量，同时引起很大的振动和磨损.为此，本文在空间直线插值算法和圆弧插值算法的基础上提出了一种改进的插补算法.同时在新的插补算法的基础上，进行了二次插值，使得新的插补算法不仅能够适用于匀速直线规划，同时可以实现运动速度和加速度的连续性.

1 空间匀速直线插补

机器手臂末端沿着预设的某条直线匀速移动到终点的过程中，对中间点位置的确定方法称为空间匀速直线插补［7］.设起点为P0(x0，y0，z0)，终点为P1(x1，y1，z1)，机器手臂移动的速度为V，则完成整个移动所需时间T为

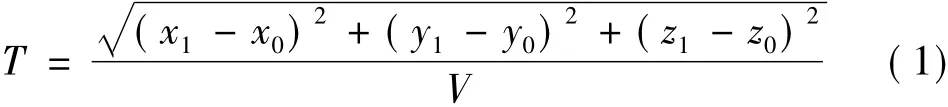
如果令插补周期为Δt，则插值的个数M为:M= T/Δt，同时有

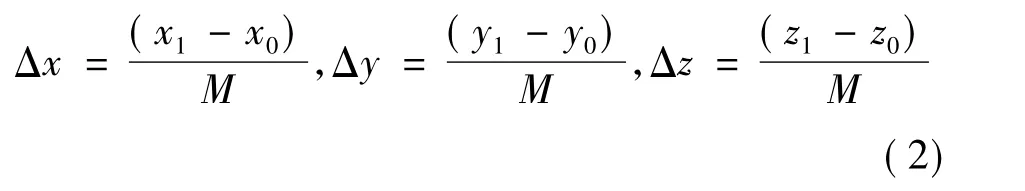
式中，Δx，Δy，Δz分别为x轴、y轴、z轴的位置增量，M取整数.那么插值点的坐标可用下式表示:

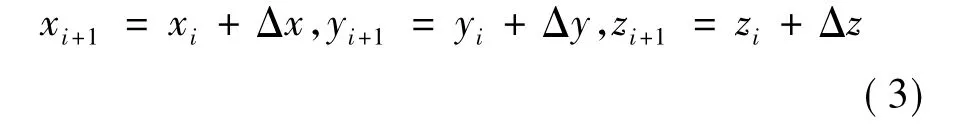
其中i取整数，取值范围为［0，M］，通过上式，各插值点的位置便可以被求出，结合逆运动学理论，便可以求得各机器手臂的关节数值，进而对手臂的各关节进行运动控制，从让使得机器手臂在末端沿直线轨迹运动.

2 空间匀速圆弧插补

空间圆弧插补通常有4个步骤:第一步，由空间三点坐标求出圆弧的圆心和半径的具体坐标;第二步，UVW坐标系的建立，空间圆弧转换为平面圆弧;第三步，UVW坐标下圆弧插补的实现;第四步，将插补后的数据，映射返回到原坐标系中［8-9］.

假设机器手臂末端需从起点P0经中间点P1到达终到达 P2处，且P0(x0，y0，z0)，P1(x1，y1，z1)，P2(x2，y2，z2)是空间上不共线的3个点.则3个点可确定一空间圆弧，设圆心为O(a，b，c)，则通过该空间圆弧的平面可用下式表示:

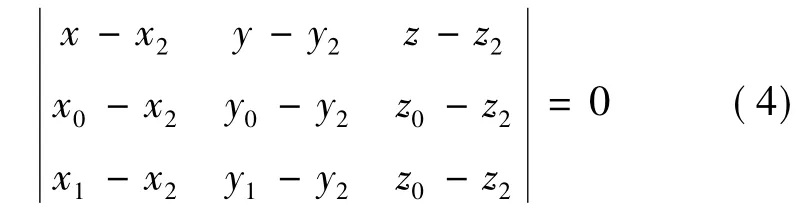
三点均在圆弧上，则有:

联立方程，便可依次求出圆心O(a，b，c)和圆弧半径R.

以圆心O为坐标原点，建立新的坐标系UVW，选取O→P0的方向作为U轴正方向，与OP0、OP1组成的平面垂直的方向作为W轴，则根据右手法则UVW坐标系即可建立，如图1所示.

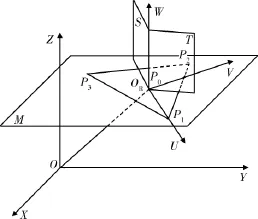
图1 XYZ-UVW坐标系图Fig.1 Coordinate system of XYZ-UVW

根据上述设定，可求出UVW三轴的方向向量分别为:

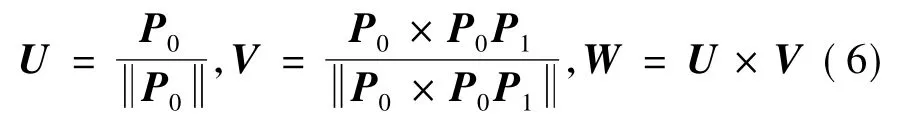
则可以求出原坐标系XYZ和UVW坐标系的变换关系T为

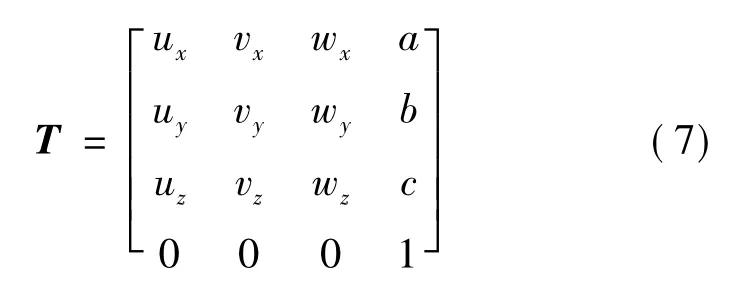
有上述的变换矩阵T，可以实现XYZ坐标系和UVW坐标系的变换:

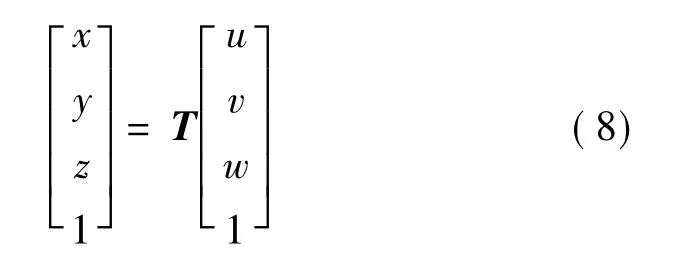
在坐标系UVW中，对于P0，P1，P2和圆心O，则有a=b=c=0;w0=w1=w2=0;u0=R.

在变换后的UVW平面内，空间圆弧转变为了一个平面圆弧，便可以开始UVW坐标系下的圆弧规划了.设起点P0到终点P2扫过的圆弧角为θ，机器手末端线速度为v，起点到终点所需时间为T.令插补周期为Δt，则插值的个数M为:M=T/Δt，第i个插补点的值θi=ωiΔt，其中ωi为圆弧运动的角速度.

则可以得出UVW坐标下插值点Pi(uvw)为，而转换到 XYZ 坐标系下 Pi=.

3 空间圆弧连接的匀速连续直线插补

空间直线插补法和圆弧插补法作为笛卡尔空间轨迹规划中最为基本的两种轨迹规划插补法.在一些简单环境工作时，无论采用哪一种单一的插补法都能较好的实现规划任务.而当机器手臂所在的工作空间比较复杂时，单一的插补法往往不能较好的完成任务.典型情况就是当机器手臂末端需要沿着两条直线连续运行时，如果简单的对两条直线进行连续的直线插值，将会使得机器手臂各关节驱动机构反复的启停动作，从而磨损机器手臂.同样在连续圆弧插补过程中，由于尖角的出现也可能影响轨迹的平滑性，给关节带来磨损.

为此，提出了一种基于空间圆弧连接的匀速空间连续直线插补法，即通过空间的圆弧来实现对两条直线的衔接，消除轨迹简单连接产生的接点尖角.

空间中的两条相交的直线可以确定一个二维平面，因此将空间中的直线转换到二维平面来分析是一个不错的选择.在图2中可以看到，空间上的直线L1和L2交于点P0，在P0点处出现尖角，为了消除其对机器手臂的不利影响，可以选取一段同时相交于两直线的圆弧Cl来实现两直线的连接，交点分别为P1和P2.则整个机器手臂的运行轨迹为从L1的起点出发经过P1点，通过圆弧Cl到达交点P2，沿直线L2到达终点.可以发现，圆弧圆心位置的确定以及圆弧半径的大小，将是轨迹规划的关键.

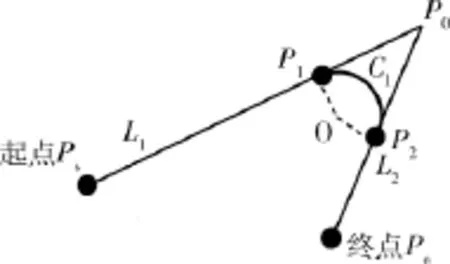
图2 直线连接图Fig.2 Linear connection diagram

为了使直线到圆弧的过渡更为流畅，做法是让所选定的圆弧和直线L1和L2同时相切，则圆弧和L1直线的切点为P1，与L2直线的相切点为P2.通过图2可以看出，由于圆弧的圆心是可以选取，因此内切于L1和L2的空间圆弧有无限多条.为了描述各圆弧相较于原始轨迹的程度，定义了一个“拟合度”F.F被定义为圆弧连接后第一段直线轨迹长度与圆弧连接前该直线轨迹长度之比.选取不同的圆弧，将对应不同的F.因此，其取值范围为［0，1］.当直线与圆弧连接点与开始点重合时，即Ps点为圆弧起点，则第一段直线轨迹长度为0，F取“0”值;又有当P1点选为L1直线的中点时，则F为“0.5”.如果设P0到P1的距离为d10，直线L1的长度为dL1，则d10= dL1×(1－F).如图2所示，由于圆弧同时相切与两直线，因此对两直线分别作垂线，则两垂线交点O(a，b，c)即为圆弧的圆心，P1或P2到O点的距离则为圆弧的半径R.

空间圆弧连接的匀速直线插补步骤如下:

步骤1.计算圆弧C1和两直线的交点坐标.

设定拟合度F，根据起始点Ps(xs，ys，zs)和点P0(x0，y0，z0)的三维坐标，可计算出连接点P1处的坐标.公式如下:

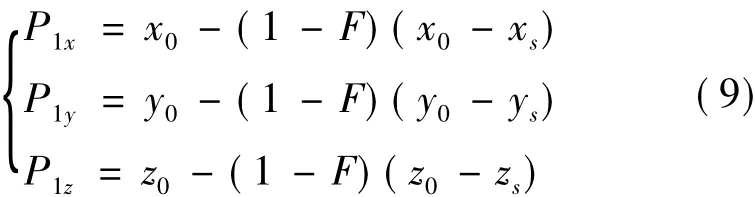
而通过结束点Pe(xe，ye，ze)和点P0(x0，y0，z0)的三维坐标，又可以计算出P2点的坐标.公式如下:

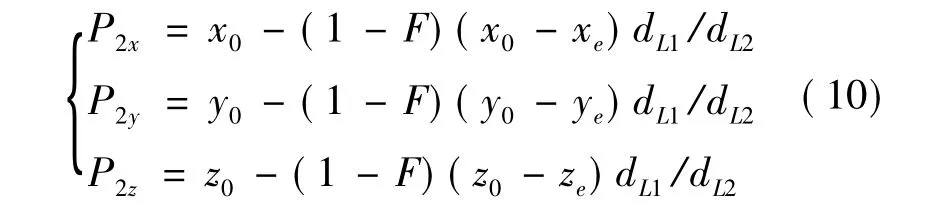
式中dL1和dL2分别为两直线L1、L2的长度.

步骤2.对Ps到P1点之间的空间直线进行空间直线插值，实现这段的轨迹规划.

步骤3.计算圆弧半径R及圆点.

根据起点Ps、终点Pe和两直线原始交点P0的坐标，利用式(4)求出平面方程.而P1和P2两点在圆弧上，因此

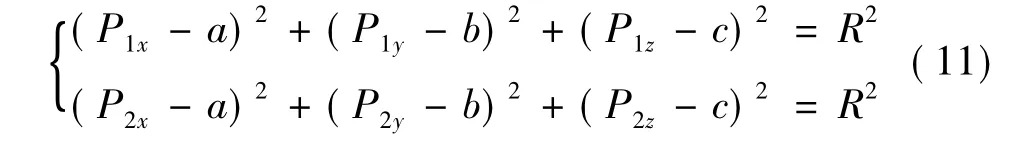
由于L1和圆弧相切，OP1的长度为圆的半径R，如图3所示.

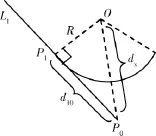
图3 圆弧和直线L1的切线Fig.3 The circular arc and tangent of the straight

观察图3，根据勾股定律则有

其中d10为P1点到P0点的距离，dx为圆心O到点P0的距离.

根据式(4)、(11)和式(12)可以求出原点O(a，b，c)的坐标值和圆的半径R.

步骤4.构建UVW坐标系.

以圆心O为坐标原点，构建新坐标系UVW，U轴的正方向选定位O→P1的方向，和OP1、OP2所组成的平面垂直的方向设为W轴，则可由右手法则得出V轴的方向.

步骤5.在UVW坐标系上完成空间圆弧插补，求出插补点Pk(uk，vk，wk)，然后得出插补点在原始坐标系XYZ上的坐标值，从而完成该圆弧段的轨迹规划.

步骤6.对于P2点到L2终端的直线段，采用空间直线均匀插值法完成轨迹规划.

通过以上6步，则可以实现空间圆弧连接的匀速连续空间直线轨迹规划.

4 空间圆弧连接的连续直线二次插补

在机器手臂的实际轨迹运行中，如果硬性的要求机器末端保持匀速运动，势必会使得机器手臂的功能受到限制.而如果简单的将上一节提出的算法应用于变运动，速度曲线将连续不平滑，同时加速度会有跳跃.为了解决机器手臂末端变速运动时存在的诸多问题，鉴于三次样条曲线具有连续的二阶导数，所以在上节提出的算法的基础上，引入三次样条曲线进行二次插值，从而使运动速度连续，加速度平滑，并且使开始点和结束点的速度加速度变为零.

三次样条曲线的方程为

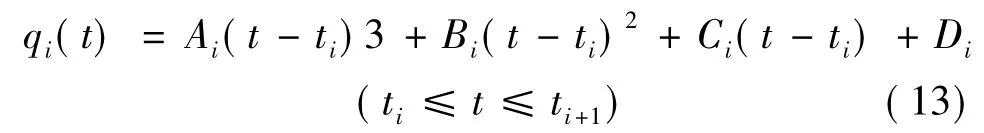
其中qi(t)为原有的两个连续节点之间的第i个插补点位姿变量.通过对方程(13)的求导及变换，可以求出多项式中的4个系数

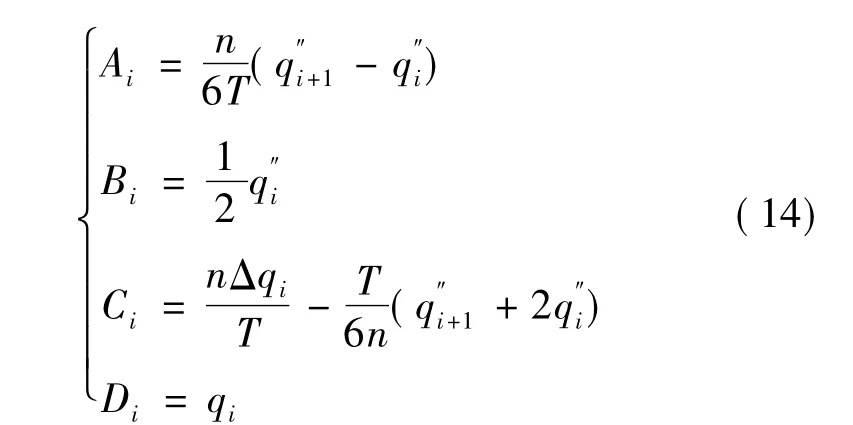
由式(14)可以看出，问题的关键在于求出q″i，对式(13)两边的求导，可知

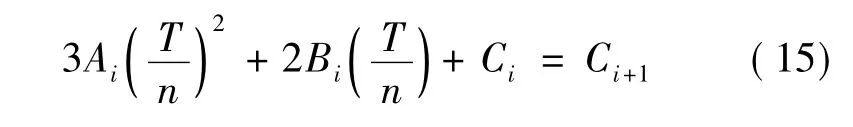
将式(14)中各系数代入式(15)，则有

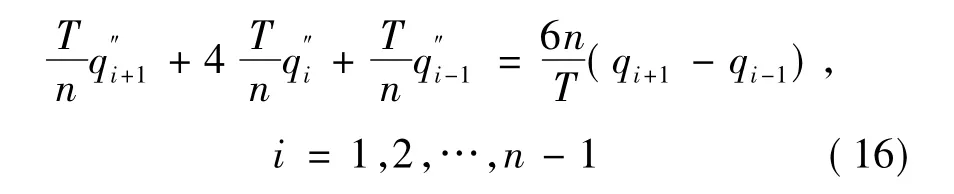
又因为自然三次样条满足:

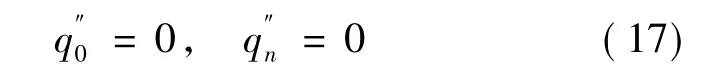
将式(16)和式(17)联合用如下矩阵形式来表示:

其中

通过对矩阵方程(18)的求解，则三次样条方程中的4个系数得以求出，进一步在给定插补周期的基础上可求出三次样条插补的各点的位姿，从而实现笛卡尔空间的二次插补.

5 仿真验证

5.1 基于空间圆弧连接的匀速连续空间直线插补法仿真

设空间内有任意3点:Ps(210，120，110)、P0(55，220，255)、Pe(48，28，70)，为了使机器手臂能够平滑运行，需要采用本文提出的空间圆弧连接连续空间直线插补算法，构建一段圆弧来代替原轨迹中的尖角.首先设定一个拟合度的初值F=0.7时，然后通过MATLAB软件来实现轨迹规划仿真，仿真效果如图4所示.

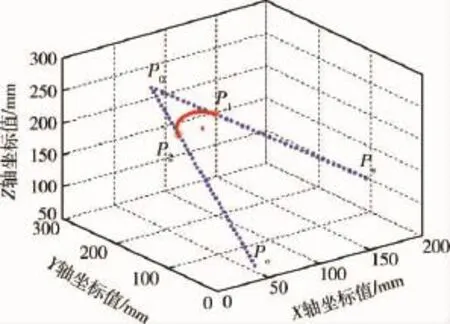
图4 基于空间圆弧连接的匀速连续空间直线插补轨迹规划图(F=0.7)Fig.4 Trajectory planning diagram of linear interpolation for uniform continuous space based on connection of spatial arc(F=0.7)

由图4可以看出，机器手臂末端将从起点出发直线运行到P1点，然后经过由P1、P2点构成的内切于两直线的圆弧，最后再沿直线方向到达终点.

若改变拟合度F=0.9，可得到另一个轨迹规划仿真图如图5所示.

图4的规划轨迹和图5类似，所不同的是两个切点的坐标发生了变化，同时圆弧的圆心坐标也发生了变化.

由图4和图5的仿真结果可以看出，本文提出的基于空间圆弧连接的匀速连续空间直线插补轨迹规划算法符合设计要求.该算法运行稳定，能够很好的解决连续直线中的尖角问题，使规划轨迹变得更加平滑，从而改善了机器手臂中各关节的磨损现象.另外，我们也可以看出，通过选取不同的拟合度，会形成不同的轨迹.实际规划中需要根据环境或规划要求，选择更为适合的拟合度.一般而言，需要高度拟合原始轨迹时，则F的取值应设置为较大值.否则，则可以将拟合度选择得较小，从而减少路程，减少时间和能量.

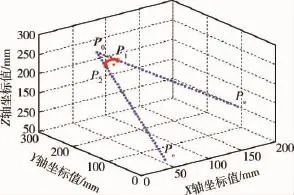
图5 基于空间圆弧连接的匀速连续空间直线插补轨迹规划图(F=0.9)Fig.5 Trajectory planning diagram of linear interpolation for uniform continuous space based on connection of spatial arc(F=0.9)

5.2 圆弧连接直线插补法的二次插值仿真

如果将上节提出的插补法简单的应用于非匀速轨迹时，在速度连续性和平滑性方面将会较差，于是在上节提出的算法的基础上进行了基于样条的二次插值，获得了不错的效果.图6和图7是机器手臂末端关节的速度随插补次序的仿真图.

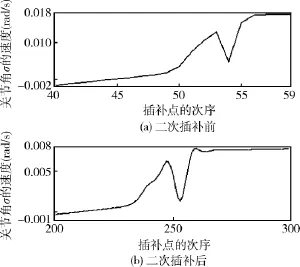
图6 末端关节速度仿真图Fig.6 The simulation diagram of the end joint velocity

通过仿真可以看出.二次插补后的插补点增多了;各关节轨迹在插值前后的轨迹都保持的较好的连续和平滑性，没有很大的变化;而二次插补后的关节速度则不仅具有之前的连续性，而且速度变得连续且平滑;关节加速度方面，在插补前，关节的加速度不连续且有跳变，而二次插补后加速度变得连续，并且在起始点和结束点加速度为零.可见，二次插补后的关节运动将更加平滑，从而使机器手臂的各关节的机械振动和冲击得以减弱.

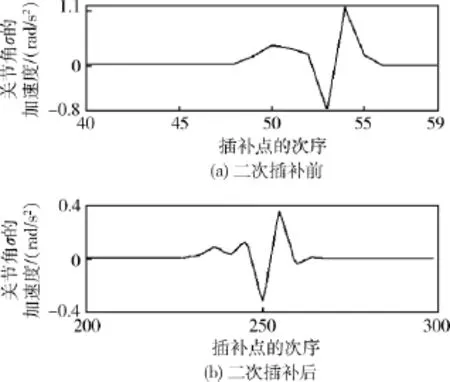
图7 末端关节加速度仿真图Fig.7 The simulation diagram of the end joint acceleration

6 结论

轨迹规划对于机器手臂而言是相当重要的，本文基于笛卡尔空间对关节型机器手臂的轨迹规划进行了分析和探索，从空间直线插值和空间圆弧插值这两种最基本的算法着手，针对空间连续直线出现尖角的问题，提出了一种基于空间圆弧连接的均值连续空间直线插补算法，并在此基础上引入了三次样条的二次插值，从而使得新的插补法在非匀速运动下也具有平滑的轨迹.最后借助于MATLAB软件对算法进行了仿真，验证了本文所提出算法的稳定性，取得了不错的效果，具有一定的实用价值.

［1］孙秀萍.机器人手臂轨迹规划的研究［J］.内蒙古师范大学学报(自然科学汉文版)，2009，38(2):174-177.

SUN X P.Research on the method of trajectory planning for A robot arm［J］.Journal of Inner Mongolia Normal University(Natural Science Edition)，2009，38(2):174-177.

［2］SHAFAAT A B，BERTRAND T.On-line computing of a robotic manipulator joint trajectory with velocity and acceleration constraints［C］//International Symposium on Assembly and Task Planning Manna Del Rey.Colombus:CA，1997.

［3］MITI R，SHINICHIRO N.Offline and online trajectory generation with sequential physical constraints［C］//International Conference on Robotics and Biomimetics，A-sian Institute of Technology.New York:IEEE，2008: 578-583.

［4］SAHAR G，HOLLERBACH J M.Planning of minimumtime trajectories for robot arms［C］//IEEE international Conference on Robotics and Automation.New York: IEEE，1984:751-758.

［5］TAYLOR R H.Planning and execution of straight line manipulator trajectories［J］.IBM Journal of Research and Development，1979，23(3):424-436.

［6］ZHANG B，FANG Q，KE Y L.Optimal time trajectory planning method for a kind of posture aligning system of large rigid bodies［J］.Chinese Journal of Mechanical Engineering，2008，44(8):248-252.

［7］周刚.垂直关节型6自由度机器人笛卡尔空间轨迹规划的研究［D］.广州:华南理工大学，2011.

［8］林威，江五讲.工业机器人笛卡尔空间轨迹规划［J］.机械工程与自动化，2014，10(5):141-143.

LIN W，JIANG W J.Trajectory planning of industrial robot in cartesian space［J］.Mechanical Engineering＆Automation，2014，10(5):141-143.

［9］林仕高.搬运机器人笛卡尔空间轨迹规划研究［D］.广州:华南理工大学.2013.

Trajectory Planning of Robotic Arm in Cartesian Space

ZHU Qingzhi，ZHANG Yi
(Henan Polytechnic Institute，Nanyang 473000，China)

Sharp corners may appear in robotic arm’s trajectory planning by using general interpolation method.In order to eliminate the sharp edges and make the machine arm have a continuous velocity and acceleration under non uniform motion state，a new circular-connection-mean linear interpolation method is proposed.Then，a quadratic interpolation is performed，under which the acceleration and deceleration have good smoothness.A simulation about the algorithm is made under the environment of MATLAB.The optimal planning path can be obtained via performing the algorithm and selecting the adjustment fitting degree.Finally，the good feasibility of the algorithm is confirmed in the robot arm’s trajectory planning.

two interpolation;robotic arm;trajectory planning;MATLAB simulation

TP242.6

A

1674-1579(2016)04-0024-06

10.3969/j.issn.1674-1579.2016.04.005

朱清智(1980—)，男，讲师，研究方向为自动控制系统的科研及教学工作;张 毅(1983—)，男，讲师，研究方向为智能控制技术.

2015-09-03