高阶重力和力矩对空间太阳能电站运动的影响*
吴志刚,刘玉亮,张开明,邬树楠
(1.大连理工大学工业装备结构分析国家重点实验室,大连116024; 2.大连理工大学航空航天学院,大连116024)
高阶重力和力矩对空间太阳能电站运动的影响*
吴志刚1,2,刘玉亮1,2,张开明1,2,邬树楠1,2
(1.大连理工大学工业装备结构分析国家重点实验室,大连116024; 2.大连理工大学航空航天学院,大连116024)
相比于传统卫星,空间太阳能电站具有超大的尺寸,高阶重力和重力梯度对其轨道和姿态运动的影响将不能再忽略.文中以地球同步拉普拉斯轨道上的太阳塔式空间太阳能电站为例,研究了在考虑地球扁率的引力场中,高阶重力和力矩对空间太阳能电站姿轨运动的影响.首先将空间太阳能电站的重力势函数进行泰勒展开,并保留至四阶项;然后求出电站所受到的重力和重力梯度力矩,并给出其轨道和姿态运动方程;最后通过数值仿真来分析不同阶次的力和力矩对轨道运动的影响.结果表明:高阶力对卫星轨道的影响较大,可达到百米量级;高阶力矩对卫星姿态运动影响则较小,可忽略不计.
高阶重力和力矩;泰勒展开;地球扁率;空间太阳能能电站
0 引言
1968年美国科学家Glaser[1]首先提出空间太阳能电站(space solar power station,SSPS)的概念.自从这一概念提出以来,多个航天大国陆续开展了相关研究.迄今为止,共有20多种概念方案被陆续提出[2].
为了保证SSPS的正常在轨运行,必须对其轨道和姿态动力学特性进行研究.在以往的研究中,航天器轨道和姿态往往是分开的,并没有考虑到它们之间的重力耦合作用[3-5].传统卫星由于其尺寸较小,其高阶重力和重力梯度力矩往往可忽略不计.但对于SSPS这种尺寸达到km量级的超大型尺寸航天器而言,高阶重力和力矩的作用将会变得显著.因此有必要对其在考虑高阶力和力矩下的动力学特性进行研究.
在关于高阶重力和力矩的研究中,Duboshin[6]首先推导了两种任意构型天体之间在考虑高阶重力和力矩下的姿轨耦合运动方程.Lange[7]研究了一种任意构型航天器在地球中心重力场中的运动,并将其引力势函数的泰勒展开式保留至ε2项,其中ε= ρ/R,ρ为航天器的特征尺寸,R为卫星运行的轨道半径,从而给出了便于计算的重力场中的姿轨耦合运动方程.Wang等[8]研究了航天器在某颗小行星引力场中的运动,分析了小行星扁率对重力姿轨耦合运动的影响.
本文以图1所示太阳塔(sun tower)式空间太阳能电站为对象,研究地球高阶重力和重力梯度力矩对SSPS姿态运动和轨道运动的影响.文章第1节在考虑地球扁率的引力场中,给出SSPS在轨运行时所受到的重力和力矩;第2节将给出SSPS的轨道运动和姿态运动方程;第3节分析不同阶次力和力矩对SSPS姿态运动和轨道运动的影响;结论将在第4节给出.
1 重力和重力梯度力矩
1.1 重力势函数
太阳塔式SSPS在地球中心重力场中的运动如图2所示.其中,Oe表示地球质心,e表示地球;R表示从Oe到卫星质心O的位置矢量;r表示从Oe到质量单元dm的矢量;ρ表示从O到dm的位置矢量.为了描述SSPS的姿态运动,这里引入两个坐标系.一个是S(i,j,k)惯性坐标系,坐标原点为Oe;i,j均位于地球赤道平面内,且i的方向Oe指向春分点,k与i,j共同构成右旋正交系;另一个是Sb(,,)航天器固联坐标系,具体定义参考文献[9].

图1 太阳塔式空间太阳能电站Fig.1 The configuration of sun tower SSPS

图2 太阳塔式SSPS在地球轨道上的运动Fig.2 A sun tower SSPS moves in earth orbit
设由固联坐标系Sb到惯性系S的坐标变换矩阵为

Rb=[和Rs=[RxRyRz]T分别表示R在坐标系Sb和S下的投影;且满足Rs=ARb.设ρb=[x y z]T,ρs=[ρxρxρy]T分别表示ρ在Sb和S下的投影,则r在Sb下的投影可表示为rb=ρb+Rb.
卫星的质量单元dm在地球中心重力场中的势函数为
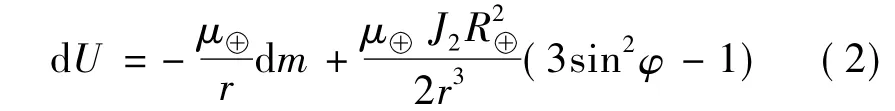

相比于传统卫星,SSPS的尺寸过大,对其求总体势函数时不能再将其当成质点来处理.对式(2)进行泰勒展开,并保留至(ρ/r)4,可得
为了便于描述太阳塔式SSPS的重力势函数,这里引入一个新的变量[10]
相比于太阳塔构型的空间太阳能电站的长(z)和宽(x),其厚度(y)只有几米,故可忽略不计.因此,x,y,z的取值范围可表示为:y=0,-h/2≤x≤h/2,-l/2≤z≤l/2.dm=σdxdz,这里σ=2.5 kg/m2为空间太阳能电站的面密度.此外,由于太阳塔式SSPS的对称构型可得


设Ixx,Iyy,Izz分别为SSPS绕固联坐标系3个轴的转动惯量;由转动惯量的定义可知:Ixx=Jyy+Jzz,Iyy= Jxx+Jzz,Izz=Jxx+Jyy.
将式(4)~(10)代入式(2)并进行积分可得SSPS的重力势函数为

1.2 重力和重力梯度力矩
由式(11)可知,重力势函数U与a1,a2无关,故势函数可写为:U=U(Rb,a3);设卫星所受到的万有引力在S下的投影为:f=[fxfyfz]T,在Sb下的投影为:F=[FxFyFz]T,则二者满足[8,11]

设卫星所受到的重力梯度力矩在航天器固联坐标系下的投影为T=[TxTyTz]T,则引力梯度力矩可以表示为[8,11]
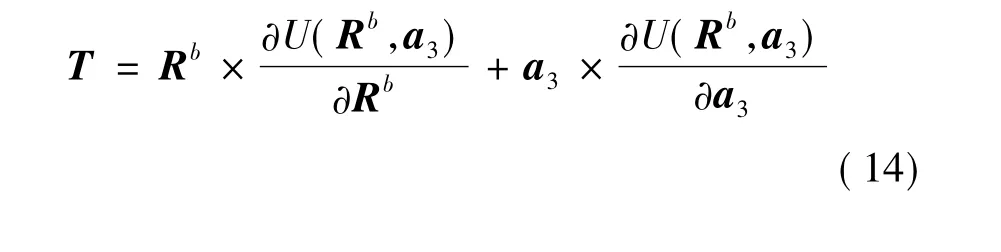
2 卫星的运动方程
卫星的轨道运动方程为

为了避免欧拉角描述姿态时存在的奇异问题,这里采用四元数来描述空间太阳能电站的姿态运动.设Sb相对于S的四元数元素为Q=(q0,q),其中q0=cos(θ/2),q=asin(θ/2).a和θ分别表示从Sb到S的旋转轴和旋转角[12].则从Sb到S的坐标转换矩阵可表示为[8]

卫星的姿态运动方程为[8]
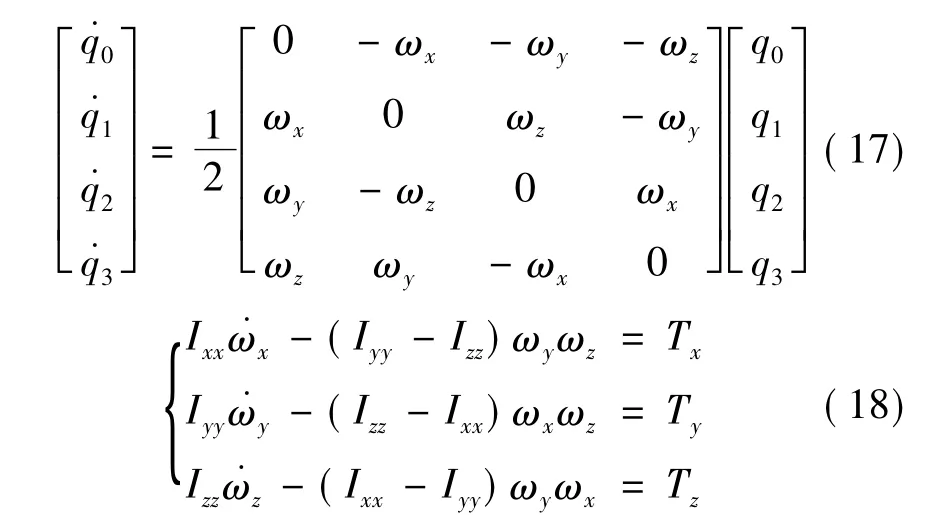
3 数值仿真
为了分析高阶重力和重力梯度力矩对SSPS轨道运动和姿态运动的影响,本节给出了一个仿真算例.其仿真结果如图3~4所示.其中,图3表示不同阶次重力的大小以及它们对SSPS轨道运动的影响.图4则表示高阶重力梯度力矩的大小以及它对SSPS姿态运动的影响.这里,为了使地球扁率引起的高阶重力和力矩不为零,选择地球同步拉普拉斯轨道作为SSPS的运行轨道.地球同步拉普拉斯轨道是一种特殊的地球同步轨道,其轨道偏心率为0,轨道倾角为7.9°,轨道半径为R1=42 164.169 km.作为SSPS一种潜在的运行轨道,地球同步拉普拉斯轨道有相比于其他运行轨道独特的优势[4];SSPS的初始条件为

式中,R0,v0分别表示SSPS位置矢量和速度在惯性坐标系S下的投影,且满足:,,i=7.9°为轨道倾角.

图3 不同阶次力的大小及其对SSPS轨道运动的影响Fig.3 The magnitude of different order gravitational force and its influence to the orbital motion of SSPS
不同阶次力对SSPS轨道运动的影响如图3左列所示.图中,Δ1(NM)表示只考虑U(0)引起的重力时轨道半径与准确值之间的差值;这里准确值是指考虑式(11)中全部势函数时SSPS轨道半径的值.Δ2(FOM)表示只考虑U(0),和时的轨道半径与准确值之间的差值;Δ3(SOM)表示只考虑U(0)和U(2)时轨道半径与准确值之间的差值.不同阶次力的大小如图3右列所示;其中,SDFF表示高阶势函数U(2),和项产生重力的大小;SOF表示U(2)项产生重力的大小;FOF表示和项产生重力的大小.从图4中可以看出,对于运行在地球同步拉普拉斯轨道上的SSPS,其高阶力对其轨道的影响可达到百米量级,且主要是由二阶力引起;而更高阶力对其轨道的影响很小,可忽略不计.

图4 高阶力矩的大小及其对SSPS姿态运动的影响Fig.4 The magnitude of different order gravitational torque and its influence to the attitude motion of SSPS
高阶力矩的大小及其对SSPS姿态运动的影响如图4所示.图4(a)表示在SSPS运行的两个周期内,只考虑U(0),U(2)时的姿态角θ(θ=2arccos(q0))与同时考虑式(11)中全部势函数时SSPS姿态角θ0之间的差值,即δ1=θ0-θ.图4(b)表示重力势函数和项产生的重力梯度力矩的大小.从图4中可以看出高阶力矩对姿态运动的影响较小,两个周期内达到的幅值约为0.2°,可忽略不计.此外,由于空间太阳能电站的对称构型,从而致使三阶势函数为零.故而导致高于二阶的力和力矩对SSPS的姿态运动和轨道运动影响较小;对于非对称构型的航天器,其高阶重力和重力梯度力矩对姿轨运动的影响需重新考虑.
4 结论
本文研究了太阳塔式SSPS运行在地球同步拉普轨道上时高阶重力和重力梯度力矩对其姿轨运动的影响.分析了不同阶次力和力矩对SSPS轨道运动和姿态运动的影响,并进行了数值仿真.结果表明:
(1)高阶力对其轨道的影响可达到100m量级,且主要由二阶力引起,高于二阶力的高阶力的影响可忽略不计;
(2)高阶力矩对其姿态的影响较小,两个周期后的误差约为0.2°,可忽略不计.但对于非对称构型的SSPS,高阶重力和力矩的影响需重新考虑.
[1]GLASER P E.Power from the sun:its future[J].Science,1968,162(3856):857-861.
[2]王立,侯欣宾.空间太阳能电站的关键技术及发展建议[J].航天器环境工程,2014,31(4):343-350.
WANG L,HOU X B.Key technologies and some suggestions for the development of space solar power station[J].Spacecraft Environment Engineering,2014,31 (4):343-350.
[3]WIE B,ROITHMAYR C M.Attitude and orbit control of a very large geostationary solar power satellite[J].Journal of Guidance Control and Dynamics,2005,28 (3):439-451.
[4]MCNALLY I,SCHEERES D,RADICE G.Locating large solar power satellites in the geosynchronous Laplace plane[J].Journal of Guidance Control and Dynamics,2015,38(3):489-505.
[5]MCNALLY I,SCHEERES D,RADICE G.Attitude dynamics of large geosynchronous solar power satellites[C]//AIAA/AASAstrodynamicsSpecialistConference.Washington D.C.:AIAA,2014.
[6]DUBOSHIN G N.The differential equations of translational-rotational motion of mutally attracting rigid bodies[J].Soviet Astronomy,1958,2:239-250.
[7]LANGE B.Linear coupling between orbital and attitude motions of a rigid body[J].Journal of the Astronautical Sciences,1970,18:150-167.
[8]WANG Y,XU S.Gravitational orbit-rotation coupling of a rigid satellite around a spheroid planet[J].Journal of Aerospace Engineering,2012,27(1):140-150.
[9]刘暾,赵钧.空间飞行器动力学[M].哈尔滨:哈尔滨工业大学出版社,2003.
[10]ASHENBERG J.Mutual gravitational potential and torque of solid bodies via inertia integrals[J].Celestial Mechanics and Dynamical Astronomy,2007,99(2): 149-159.
[11]MOHAN S N,LANGE J V,LANGE B O.Interaction between attitude libration and orbital motion of a rigid body in a near Keplerian orbit of low eccentricity[J].Celestial Mechanics,1972,5(2):157-173.
[12]张荣辉,贾宏光,陈涛,等.基于四元数法的捷联式惯性导航系统的姿态解算[J].光学精密工程,2008,16(10):1963-1970.
[13]徐小明,钟万勰.基于四元数表示的一种改进的刚体动力学保辛积分[J].应用数学和力学,2014,35 (11):1177-1187.
XU X M,ZHONG W X.An improved symplectic integration for rigid body dynamics in terms of unit quaternions[J].Applied Mathematics and Mechanics,2014,35(11):1177-1187.
[14]UDWADIA F E,SCHUTTE A D.An alternative derivation of the quaternion equations of motion for rigid-body rotational dynamics[J].Journal of Applied Mechanics,2010,77(4):044505-1.
[15]XU X,ZHONG W.On the numerical influences of inertia representation for rigid body dynamics in terms of unit quaternion[J].Journal of Applied Mechanics,2016,83(6):061006-11.
The Influences of Higher Order Gravitational Force and Torque to the Motion of Space Solar Power Station
WU Zhigang1,2,LIU Yuliang1,2,ZHANG Kaiming1,2,WU Shunan1,2
(1.State Key Laboratory of Structural Analysis for Industrial Equipment,Dalian University of Technology,Dalian 116024,China; 2.School of Aeronautics and Astronautics,Dalian University of Technology,Dalian 116024,China)
Comparing to traditional satellites,space solar power stations have large size.The influences of higher order gravitational force and torque to the orbital and attitude motion should be considered carefully.The influences of higher order gravitational force and torque to the orbital and attitude motion of a sun Tower space solar power station working in the earth’s gravitational field which the oblateness of earth is considered will be studied in this paper.Firstly,the gravitational potential function will be expanded in a Taylor series up to fourth order;Secondly,the gravitational force and torque of a solar power station will be derived and the equations of the attitude and orbital motion of solar power station are given.At last,the influence of the higher order gravitational force and torque to the orbital and attitude motion will be analyzed by numerical simulation.The result shows that the influence of the higher order gravitational force to the orbital motion can reach the order of 100m and the influence of the higher order gravitation torque to the attitude motion is small enough to be neglected.
higher order gravitational force and torque;Taylor expansion;earth oblateness;space solar power station
V412.4
A
1674-1579(2016)04-0001-05
10.3969/j.issn.1674-1579.2016.04.001
吴志刚(1971—),男,教授,研究方向为航天器动力学与控制的研究;刘玉亮(1991-),男,博士研究生,研究方向为大型航天器轨道动力学,姿态动力学与控制研究;张开明(1992—),男,博士研究生,研究方向为大型结构姿态动力学与控制;邬树楠(1982—),男,博士,研究方向为航天器的姿态控制方法.
*国家自然科学基金资助项目(11432010&11502040)和中央高校基本科研资助项目(DUT15LK31).
2016-06-29

