航天器的有限时间时变滑模姿态控制方法设计*

耿 洁，吕 楠，王 韬，宫经刚

(北京控制工程研究所，北京100190)

航天器的有限时间时变滑模姿态控制方法设计*

耿 洁，吕 楠，王 韬，宫经刚

(北京控制工程研究所，北京100190)

本文研究具有参数不确定性和外部扰动的航天器姿态控制问题.针对修正罗德里格参数表征的航天器姿态模型提出一种有限时间时变滑模函数，在此基础上设计一种有限时间收敛的滑模姿态控制方法，并证明其稳定性，给出控制参数的设计方法.该方法在保证系统渐近稳定的前提下，不仅能够实现姿态跟踪误差在有限时间内收敛，而且能够实现姿态跟踪误差在设定的时间收敛，且全局具有滑模动态确定的系统响应.通过仿真结果验证本文提出方法的有效性.

航天器;姿态控制;滑模控制;有限时间收敛;设定时间收敛

0 引言

航天器姿态控制系统是一个复杂的非线性系统，具有转动惯量不确定性等参数摄动，且在轨运行时易受空间环境中各种无法精确描述的干扰影响，例如重力梯度、太阳光压、地球磁场等，经典控制理论已无法满足日益增长的需求，具有较好鲁棒性的航天器姿态控制方法日益受到重视［1-2］.

滑模控制可以在改善系统响应特性的同时，使闭环系统针对系统的参数摄动、外部干扰等不确定性具有较强的鲁棒性和适应性［3］，具有响应速度快、对参数及外加干扰不灵敏、无需系统在线辨识、物理实现简单等优点，近年来在航天器控制系统中得到了广泛的应用［4］.

滑模控制首先根据期望的系统状态或误差响应预先设计一个稳定的运动模态(滑模面)，然后设计控制律将系统轨迹引导至该预定的模态，并迫使系统轨迹在以后的时间里按照该模态运动.基于传统滑模面的控制律设计方法主要采用线性滑模函数，这种滑模函数仅仅能够保证姿态跟踪误差的渐近收敛，而由于有限时间控制常常能够实现更快的收敛速度和更好的控制性能［5］，在工程实际中，常常希望姿态跟踪误差在有限时间内收敛.为了提高滑模控制系统的收敛速度，有学者提出了有限时间收敛的滑模控制方法——终端滑模，在滑模函数中引入终端吸引因子，使得系统状态能在有限时间收敛到平衡点［6-7］.文献［8-9］采用终端滑模方法为存在外界扰动和不确定参数的航天器设计了姿态控制器，取得了良好的收敛速率和控制精度.

采用滑模控制的系统运动可分为两个阶段:系统相轨迹到达滑模面之前的到达段和系统相轨迹沿滑模面滑动到原点的滑模段.在现有有限时间滑模控制律的作用下，非线性控制系统只有在系统状态处于滑模段时才具有对匹配参数不确定性和外部干扰的不敏感性，当系统状态处于到达段时，不仅不具备这种不敏感性，而且无法解析地确定滑模姿态控制律作用下的系统响应.另外，在现有有限时间滑模姿态控制律作用下，姿态跟踪误差的收敛时间无法精确估计，对于期望的收敛性能，缺乏系统的参数选择方法.

针对上述问题，本文针对修正罗德里格参数描述的航天器模型，开展了有限时间滑模姿态控制方法研究，提出了一种有限时间滑模姿态控制律，并给出了滑模参数选择方法，实现了姿态跟踪误差在设定的时间收敛，并保证了系统对参数不确定性和外部干扰的全局不敏感性.

1 数学模型及问题描述

用表示惯性参考坐标系，表示本体坐标系.考虑下述刚体航天器姿态运动方程

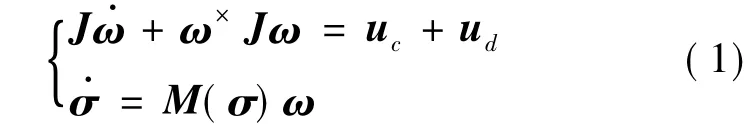
式中:J∈R3×3为航天器的转动惯量阵，考虑转动惯量不确定性时，J可以表示为J=J0+ΔJ，其中J0为转动惯量标称值，ΔJ为转动惯量不确定性;uc∈R3和ud∈R3分别表示控制力矩向量和有界的外部干扰力矩向量;ω为FB相对于FI的角速度向量，ω×表示ω的反对称矩阵，定义为

σ∈R3为航天器惯性姿态的修正罗德里格参数(modified rodrigues parameters，MRP)向量表征，采用这种姿态描述参数可以避免姿态描述中的奇异点［10］.

用FD表示航天器期望的本体坐标系，FD相对于FI的期望MRP姿态为σd∈R3，期望角速度为ωd∈R3，并假设ωd充分光滑，且其导数有界.定义当前MRPσ相对于期望MRPσd的姿态:

当前角速度ω相对于期望角速度ωd的误差角速度向量ωe∈R3定义为

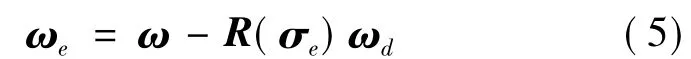
式中，R(·)∶R3→R3×3为姿态转移矩阵算子

为了表述清晰起见，下文将M(σe)，m(σe)和R(σe)简记为M，m，R.

根据式(1)～(5)，航天器姿态跟踪系统的相对姿态运动方程可表示为

本文的控制目标可总结如下:针对航天器姿态跟踪控制系统(6)，设计控制律uc，使航天器在有限时间内跟踪上给定姿态，并保持对给定姿态的跟踪.

2 控制器设计

针对上节所提出的姿态跟踪控制问题，定义滑模函数如下:

式中，s∈R3为滑模函数，k＞0为滑模函数增益，f(t)=［f1(t)，f2(t)，f3(t)］T为连续可微的时变函数向量，选择参数的值使f(t)满足下列条件:

条件1.

即

条件2.

条件1表示滑模函数初始值为零，即系统状态在初始时刻位于滑模面上.条件2表示时变函数f(t)的截断时间即为期望的收敛时间，且滑模函数及其导数在该值处连续.当设定期望的收敛时间，本文选择f(t)为如下形式的截断函数

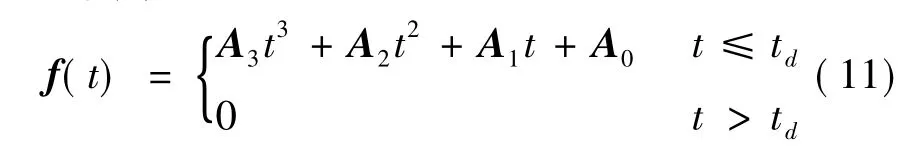
其中Ai=［Ai1Ai2Ai3］T∈R3(i=0，1，2，3)为待定的常数矩阵，其具体选择方法将在后文进行详细探讨.

在式(7)所示滑模函数的基础上，设计滑模姿态跟踪控制律如下:

计算机网络技术应用需要从业人员在掌握一定基础理论知识的前提下，根据不同网络系统的需求对技术机型有效的应用与部署，对于从业人员除了需要有较强的专业技能以外仍然需要一定的理论知识。因此，高职计算机网络技术专业教学能否将理论与技有效的融合，并有效地让学生接收成为专业教学改革的核心内容。

定理1.对于式(6)所示的航天器姿态跟踪控制系统，选择式(7)所示的滑模函数，且选择时变函数f(t)使式(9)(10)所示的条件满足，在姿态控制律式(12)的作用下，系统状态将全局处于滑模段运动，即对于任意t∈［0，+∞)，有s(t)=0.

证.对滑模函数式(7)求导，有

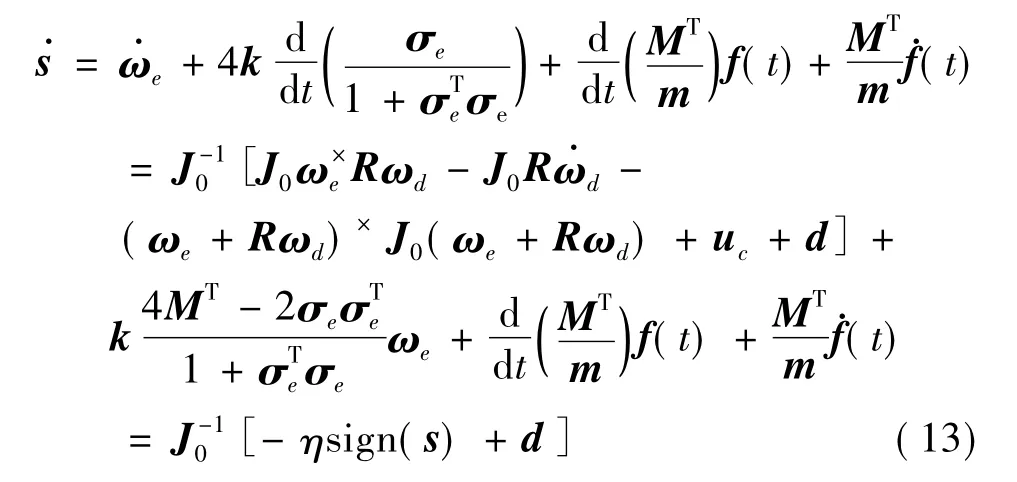
因此，Lyapunov函数递减，即V(t)≤V(0)，由于选择的滑模函数满足s(0)=0，因此V(0)≤0.又由V的定义，V≥0，因此，对于任意t∈［0，+∞)，有V(t)=0，s(t)=0.

根据上述定理，系统全局处于滑模面s=0上，根据式(7)有

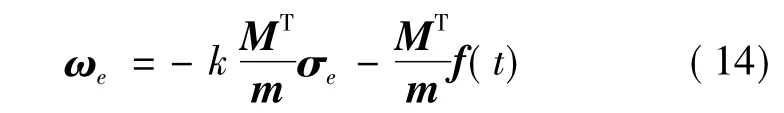
即系统动态由式(15)决定.因此可以通过调节时变函数f(t)的参数调节姿态跟踪误差的响应.当选择式(11)所示的f(t)，求解式(15)所示的微分方程可以得到具有如下形式的姿态跟踪误差响应曲线

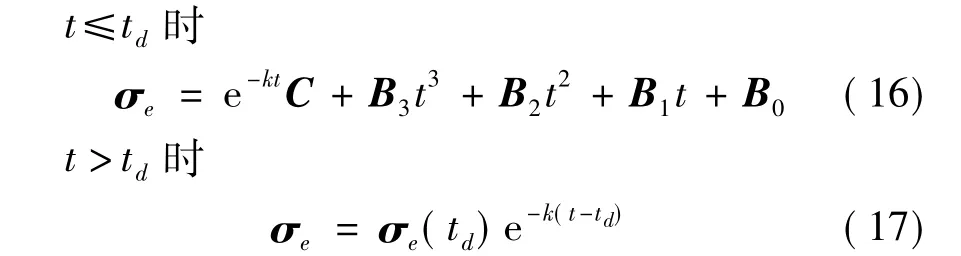
式中，C=［C1C2C3］T，Bi=［Bi1Bi2Bi3］T，i=0，1，2，3为常值系数.将式(16)代入式(15)，比较相关的各项系数可得

至此，式(16)中的C，Bi均可用Ai表示.由于期望收敛时间为，令式(16)中σe(td)=0，即

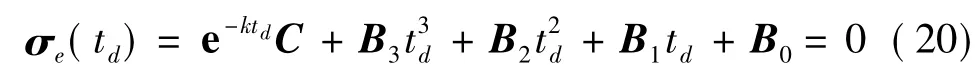
将式(9)、(10)、(20)联立，建立方程组如下:

由于Bi，C均为Ai的线性函数，上述方程组为关于Ai(i=0，1，2，3)的四元一次线性方程组，可以解出Ai(i=0，1，2，3)的值，该组参数使σe(td)=0.根据式(17)可知，当σe(td)=0，对于任意，σe(t)=0.

综上，如果按照式(21)选择滑模函数的参数Ai(i=0，1，2，3)，姿态跟踪误差σe在设定的时间收敛到零，跟踪误差响应曲线如下

本节设计的滑模函数和姿态控制律具有如下优点:1)系统状态全局位于滑模面上，因此对外部干扰和不确定性具有全局不敏感性.2)通过本节给出的参数选择方法，可以实现姿态跟踪误差在设定的时间收敛，并且给出了姿态跟踪误差的响应曲线，可以根据实际收敛速度的需求选择滑模函数参数.

3 仿真结果

本节通过航天器姿态控制的数值仿真验证本文提出的有限时间滑模控制算法的有效性.选择航天器标称转动惯量阵为

假设转动惯量存在－10%的不确定性，并给定正弦形式的外部干扰力矩

以半长轴为6 900 km，升交点赤经为60°，近地点幅角为0°，轨道倾角为0°的轨道为例，设计有限时间滑模控制律实现航天器对地定向，期望角速度为［0 －0.001 1 0］T(°)/s，给定卫星初始角速度为0，初始MRP为［－0.128 0.515 0.128］T.

首先设定期望收敛时间td=50 s，选择滑模函数参数k=0.2，η=15，其他参数的值根据式(21)计算。

为了削弱滑模的抖振现象，可将控制律(12)中的符号函数用饱和函数sat(s)=［sat(s1)，sat(s2)，sat(s3)］T取代，sat(si)定义为

其中l为边界层厚度，此时由于边界层的引入，当|si|＞l时，控制律与其稳定性证明与符号函数相同，当|si|≤l，式(13)转化为:].

选择与定理1中同样的Lyapunov函数，可得V及姿态误差收敛于0的一个较小邻域.

选择边界层厚度l=0.001.图1和图2比较了采用式(12)所示控制律和引入饱和函数的控制律的仿真结果.采用符号函数时，控制力矩输出存在明显的抖振，不利于实际应用.而引入饱和函数后，控制力矩平滑无抖振.因此后续仿真均采用了引入饱和函数的控制律.

为了验证本文提出的控制律在设定的时间内实现姿态跟踪的性能，分别设定3个期望收敛时间td=30 s，50 s，70 s，对于每一个设定的收敛时间，根据式(21)计算得到参数Ai的值，该过程可通过计算机程序离线完成，η=15.

图1给出了有限时间时变滑模姿态控制律控制下的MRP误差曲线，在参数不确定性和外部干扰的影响下，该控制律能够以较高的控制精度完成姿态控制任务，姿态角跟踪误差实现了在给定的时间收敛.图2给出了姿态角速度响应曲线，图3给出了控制力矩曲线，控制力矩平滑过渡，无突变和抖振.

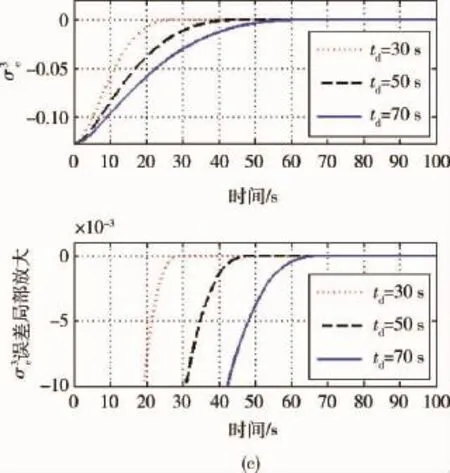
图1 不同给定时间下的姿态MRP仿真结果Fig.1 Response of MRP attitude with different convergence time

图2 不同给定时间下的姿态角速度仿真结果Fig.1 The responses of angular rates with different convergence time

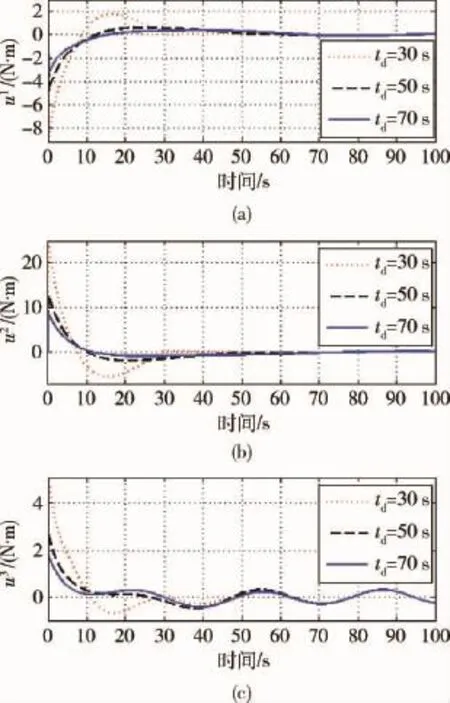
图3 不同给定时间下的控制力矩仿真结果Fig.3 The responses of control torque with different convergence time

4 结论

本文研究了具有参数不确定性和外部扰动的刚体航天器姿态控制问题，提出了一种有限时间滑模姿态控制算法，并给出了控制参数的设计方法，实现了姿态跟踪误差在设定的时间收敛，同时，实现了全局滑模，解析地确定了滑模姿态控制律作用下的系统响应.仿真结果验证了提出方法的有效性.

［1］张景瑞，张威泰，曾祥远，等.考虑不确定性的航天器姿态滑模控制器设计［J］.北京理工大学学报，2001，31(10):1198-1201.

ZHANG J R，ZHANG W T，ZENG X Y，et al.Robust controller design for the attitude control of spacecraft with uncertainty［J］.Transactions of Beijing Institute of Technology，2001，31(10):1198-1201.

［2］袁国平，史小平，李隆.航天器的自适应鲁棒姿态控制器设计［J］.系统工程与电子技术，2012，34(12): 2524-2528.

YUAN G P，SHI X P，LI L.Adaptive robust attitude maneuvering control for rigid spacecraft［J］.Systems Engineering and Electronics，2012，34(12):2524-2528.

［3］UTKIN V I.Sliding modes in control and optimization［M］.Berlin:Springer-Verlag，1992:10-11.

［4］马克茂.大型空间飞行器的高阶滑模姿态控制律设计［J］.控制与决策，2013，28(2):201-204.

MA K M.Design of higher order sliding mode attitude control laws for large-scale spacecraft［J］.Control and Decision，2013，28(2):201-204.

［5］WANG X，SUN X，YE H.Finite-time position tracking control of rigid hydraulic manipulators based on highorder terminal sliding mode［J］.Proceedings of the Institution of Mechanical Engineers，Part I:Journal of Systems and Control Engineering，2012:226，394-415.

［6］MAN Z H，YU X H.Terminal sliding mode control of MIMO linear systems［J］.IEEE Transactions on Circuits and Systems，1997，44(11):1065-1070.

［7］FENG Y，YU X H，HAN F L.On nonsingular terminal sliding-mode control of nonlinear systems［J］.Automatica，2013，49:1715-1722.

［8］WU S N，RADICE G，GAO Y S，et al.Quaternionbased finite time control for spacecraft Attitude tracking［J］.Acta Astronautca，2011，69(1-2):48-58.

［9］ZHU Z.XIA Y Q，FU M Y.Attitude stabilization of rigid spacecraft with finite-time convergence［J］.Robust Nonlinear Control，2011，21(6):686-702.

［10］CRASSIDIS J L，MARKLEY F L.Sliding mode control using modified rodrigues parameters［J］.Journal of Guidance，Control and Dynamics Control，1996，19 (6):1381-1383.

A Novel Finite-Time Sliding Mode Attitude Controller for Spacecraft

GENG Jie，LYU Nan，WANG Tao，GONG Jinggang
(Beijing Institute of Control Engineering，Beijing 100190，China)

The problem of spacecraft attitude control is investigated in this paper.To solve this problem，a finite-time sliding mode control strategy is proposed based on a finite-time time-varying sliding manifold in the present of uncertainty and external disturbance.The stabilization is proved and the parameter selection method is given.By using the proposed control strategy，the closed-loop system is asymptotically stable and the convergence time is finite.In addition，the attitude tracking error can converge in a given time.Consequently the dynamic response of the closed-loop system is determined by the sliding mode dynamics.Numerical simulations are finally provided to illustrate the performance of the control strategy.

spacecraft;attitude control;sliding mode control;finite-time convergence;convergence at a given time

V448.2

A

1674-1579(2016)04-0030-06

10.3969/j.issn.1674-1579.2016.04.006

耿 洁(1986—)，女，工程师，研究方向为非线性控制、航天器姿态控制、卫星控制分系统等;吕 楠(1980—)，男，高级工程师，主任设计师，研究方向为航天器姿态轨道控制、卫星控制分系统设计等;王 韬(1984—)，男，工程师，研究方向为航天器姿态轨道控制、卫星控制分系统设计与测试等;宫经刚(1981—)，男，高级工程师，研究方向为航天器综合电子系统设计、姿态轨道控制等.

*国家自然科学基金资助项目(61573060).

2016-02-26