思维导图在数学解题教学中的运用

董荣森

摘 要：在数学解题教学中运用思维导图，教师把自己的解题思维导引给学生，同时学生的解题思维也暴露给了教师，有利于教师进行有针对性的教学，从而提高学生学习数学的效率，加强学生对知识的理解，培养学生的目标意识和发散思维能力。

关键词：思维导图；解题教学；问题驱动

在数学解题教学中，我们不难发现很多学生对于熟悉的问题能够迅速解决，当面对新情境下的陌生问题有时无所适从或难以入手，其原因可能是多方面的. 依据波利亚的“怎样解题表”来分析，笔者认为核心问题是学生不能根据题意拟定出一个合理的解题方案.因此，要让学生学会解题，教师必须把自己的解题思维导引给学生，同时也要让学生把解题思维暴露给教师.解题思维包括三个心理活动阶段——收集解题所需的信息；对信息进行整理、加工、处理得出解法；保持这个解法的信息.学生解题时往往在信息整理、加工、处理（即寻找结论与条件的关系）这一环节中存在较大的困难，也是学生能否拟定一个合理解题方案的主要障碍. 究其原因有的是收集解题信息不全导致难以寻找到解决问题的突破口，有的是对获取的信息不知如何转换，有的是寻找不到问题结论与题设条件之间的合理联系.

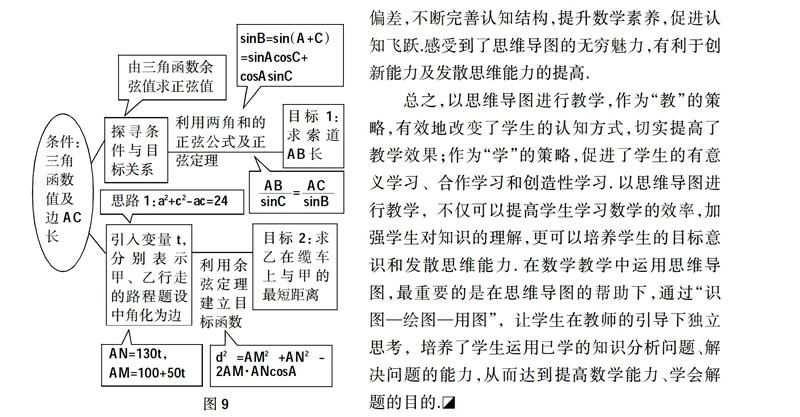
要突破解题思维这一难点，笔者尝试运用思维导图的教学策略，融目标意识、探究元素于其中，引领学生拟定合理的解决问题方案，优化解题策略与过程，有效培养学生的思维能力和解题能力. 思维导图是在20世纪70年代，由英国心理学家托尼·巴赞提出，是一种综合运用文字、符号、图片、色彩等的图形思维工具，它是基于对人脑的模拟，将抽象性思维具体化，并以直观形象的方式表征知识，有效呈现知识间的联系，体现思维过程. 本文中的思维导图与上述概念有联系也有区别，是指在解题时用来组织和表征目标与条件之间的工具，通常将某问题（或辅助命题）置于椭圆或方框之中，然后用连线将相关的问题和命题连接，连线上标明两个问题之间所运用的数学概念、定理、思想与方法，让解题更具有针对性、目的性和实效性.

笔者以一节高一“正弦定理、余弦定理的应用”复习课为例，以思维导图引领解题教学，在教学过程中，以问题驱动为依托，引导学生梳理与建构知识网络图；以思维导图为抓手，强化学生解题的目标意识和探究意识；以解决高考真题为导向，体悟思维导图的无穷魅力，体验学习数学的快乐与成功. 让学生尝试在构建思维导图的过程中，学会分析问题即寻找目标与条件之间的关系，学会拟定合理的解决问题方案，逐步养成自主绘制思维导图的习惯，并在实践中不断优化解题方案，进而达到学会解题的目的.