关注预设 重视生成 基于对话——“函数的单调性”的教学实录与反思

■浙江省温州中学　刘旭飞



关注预设重视生成基于对话——“函数的单调性”的教学实录与反思

■浙江省温州中学刘旭飞

当前，概念教学中有些现象很令人担忧：教师重解题技巧，轻概念生成，追求概念教学最小化和习题讲解最大化；学生认为概念学习单调乏味而不重视它，对基本概念死记硬背、不求理解.直接后果表现为学生在没有真正理解概念的情况下匆忙去解题，使得他们只会模仿教师解决典型例题的题型，一旦遇到新的情况、新的题型就束手无策，进而导致教师和学生为了提高成绩，陷入无休止的题海之中.

事实上，一个数学概念的背后往往蕴含着丰富的数学思想，有的数学概念本质上就是一种数学观念，是一种分析、处理问题的数学方法.重视概念的自然生成可以使学生对原有知识、技能进行再认识、再加工，进一步深化提高，把头脑中已有的认知能力调动起来，积极参与到新的学习活动中，加深对新知识的理解和认识.最近，笔者在一次市级研讨会上执教了一节研讨课“函数的单调性”，本着“关注预设，重视生成”的理念，采用“问题引领，对话交流”为主线的教学模式，学生积极主动、师生对话交流通畅，取得了较好的教学效果，获得了听课专家和教师的好评.现将本节课的课堂教学实录呈现如下，并谈谈自己的教学设计意图和教学反思，敬请同行指正.

一、课堂教学实录

1.创设情境，引入课题

我们知道函数是描述事物运动变化规律的数学模型，而生活中有很多运动变化的现象值得我们去关注．

例1图1是温州市今年某天24小时内气温随时间变化的曲线图，观察图形，你能得到什么信息？

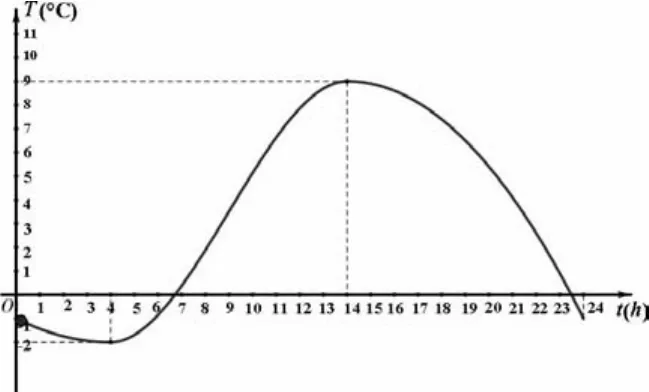
图1

设计意图：通过学生熟悉的实际问题引入课题．为概念学习创设情境，拉近数学与现实的距离，激发学生的求知欲，调动学生主体参与的积极性．学生通过观察天津市某天气温变化曲线图的变化趋势，完成对单调性直观上的一种认识．

生：（七嘴八舌）气温在0~4时下降，4~14时上升，14~ 24时又下降.

生：一天中有最低气温-2℃，最高气温9℃，温差为11℃.

师：同样一幅图，有些同学关注的是随着时间的流逝，温度先降低后升高再降低，有些同学关注的是最低气温和最高气温，各人看法不一样，各人观察点也不尽相同，这节课我们关注函数图像的上升或下降的情况（利用几何画板的动画工具让图像上一点从左到右运动并追踪让学生直观地感受图像的下降与上升）．图像在某区间上（从左往右）“上升”或“下降”的趋势反映了函数的一个基本性质——单调性（板书课题）.

师生活动：教师提问，学生思考、回答，教师根据学生回答的情况加以补充．

2.自主探究，形成新知

个人独立完成或学习小组合作完成.

问题1：任意写出一个函数的解析式，利用描点法作出它的图像，并观察当自变量变化时，函数值有什么变化规律？

设计意图：体会函数f（x）=x的图像是上升的，函数f（x）=x2的图像在y轴左侧是下降的，在y轴右侧是上升的．从形的角度初步认识函数的单调性．

师生活动：学生利用描点画出函数的图像，并观察当自变量变化时，函数值有什么变化规律，教师引导得到单调性的“形”的定义．

学生展示成果.

生：两个函数的性质如图2、图3所示.

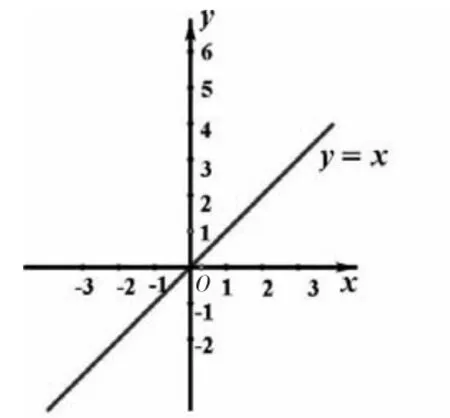
图2

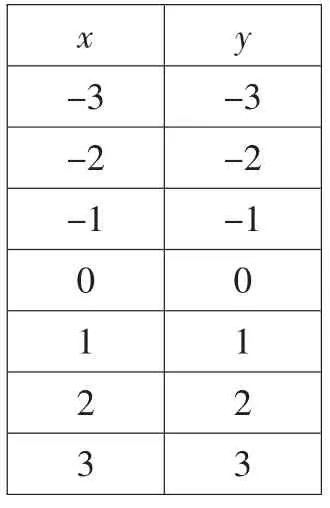
x y -3　-3 -2　-2 -1　-1 0 0 1 1 2 2 3 3

图3

x y -3　9 -2　4 -1　1 0 0 1 1 2 4 3 9

生：函数f（x）=x的图像在整个定义域上（从左向右看）成上升趋势，f（x）=x2的图像在x＜0时成下降趋势，在x＞0时成上升趋势.

师：很好.函数图像（从左向右）总是上升的，反映在自变量和应变量上就是y随x的增大而增大，图像具有这种特征的函数，我们就称它是单调递增的.

师：（板书）设函数的定义域为I，区间D⊆I．在区间D上，若函数的图像（从左向右）总是上升的，即y随x的增大而增大，则称函数在区间D上是递增的，区间D称为函数的单调增区间.（学生类比定义“递减”，接着回到前面以温度变化为背景的函数，让学生准确回答单调性）

设计意图：从图像直观感知到文字描述，完成对函数单调性的第一次认知．明确相关概念，准确表述单调性．借此强调函数的单调性是相对某区间而言的，是函数的局部性质．

师追问：刚同学画的f（x）=x2的单调性如何？

生：从图像可知，在区间（－∞，0）上递减，在区间（0，+∞）上递增．

生：（有点使坏）某同学画的是区间［－3，3］上的图像，在区间［－3，3］外看不出单调性.

师：（稍停顿，有点意外）同学画的是区间［－3，3］上的图像，在区间［－3，3］外看不出单调性，也就是说你怎么保证x＞3时图像是一直上升的，不会下降呢？

师：函数图像虽然直观，但是缺乏精确性，而且我们只能画出有限的区域，况且有些函数我们根本不知道它的图像是何形状，看来仅仅从形上认识单调性还是不够的，还得从数的角度进一步去认识它．

设计意图：借此认知冲突，让学生意识到学习符号化定义的必要性，自然开始探索.

问题2：如何从代数的角度说明函数f（x）=x2在区间（0，+∞）上是增函数，即“y随x的增大而增大”？

设计意图：结合图、表，学生在教师的引导下，结合其初中的认知基础，用数学符号语言“函数f（x）=x2，在区间（0，+∞）上任取两个数x1，x2，当x1＜x2时，有f（x1）＜f（x2）”来描述“f（x）随着x的增大而增大”，学生经历从直观到抽象，从无限到有限，从图形语言到数学符号语言，进而理解增函数、减函数、单调区间概念的过程．

生：我觉得增大必须是要有两个数之间的比较，所以可取两个数x1，x2及对应的两个函数值f（x1）和f（x2）来比较大小关系，比方说：f（2）=4，f（1）=1，f（4）＞f（1）．

生：（大声说）不行，看二次函数f（x）=x2的图像，f（2）=4＞f（－1）=1，但在区间［－1，2］上并不是增函数.师：两个不行，那三个行不行？生：（所有学生）不行.

师：那怎么办？（不动声色）

生：（笑着说）那就一直取下去，取无数个.师：怎么取？

学生或若有所思，或摇头，或窃笑，……

生：若在区间（0，+∞）上有无数个自变量x1，x2，x3，…，当x1＜x2＜x3＜…时，都有f（x1）＜f（x2）＜f（x3）＜…，就能说函数f（x）在（0，+∞）上是单调增函数．

师：这样能不能保证递增了呢？

生：（很激动）不行，我有反例，可以画图说明（上黑板画了一个反例图，如图4）.

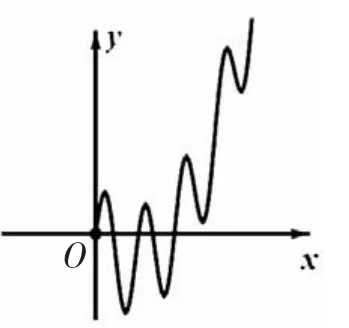
图4

师（追问）：连无数个也不能保证函数递增，那怎么办？

生：（犹豫了会）我觉得要所有的都取完，但不知道怎么取.（所有人都笑了）

师：怎样才能把所有的值都取完呢？难道我们一定要取验证区间上所有的值吗？实数上，我们如果真的取验证区间上所有的值的话，操作起来也是很困难的，能不能想个办法，用有限变量的验证来实现这种所有变量的验证呢？（同组讨论）

学生在教师的一步步设疑、启发下，到了“愤”“悱”状态.

生：我觉得可以在区间［0，+∞）上，任取两个x1，x2，得到f（x1）=x21，f（x2）=x22，如图5，当x1＜x2时，有f（x1）＜f（x2），则说明函数f（x）= x2在［0，+∞）上为增函数．

师：你们同意他的做法吗？（掌声响起）

图5

师：做得非常好.在区间［0，+∞）上，任意取了两个值，证得自变量大的函数值也大，这样我们就通过两个任意变量的验证实现了所有值的验证.

师（追问）：一定要两个都任意吗？一个行不行？（稍停顿）即对于区间［0，+∞）上任意的x，有f（x）＞f（0），能否说函数f（x）在区间［0，+∞）上单调递增？

生：不行，刚某**同学画的图可说明.

师：三个呢？

生：没必要.

设计意图：让学生体会一个任意不够，三个任意没必要，两个刚刚好．

问题3：如何用准确的数学符号语言刻画函数y=f（x）（定义域为I）在区间D上递增？

师生活动：学生在学案上自主尝试概括定义，投影学生概括的定义，学生点评，教师补充，板书增函数的定义，同组讨论指出定义中的关键之处．

问题4：类比增函数的定义，我们应当如何给减函数下定义？

设计意图：得出减函数的定义，从而培养学生的类比能力．

师生活动：小组讨论，代表发言交流．教师引导学生通过类比、观察、验证、交流后，得出减函数定义，并给出单调区间的概念.

3.巩固提高，应用新知

师生活动：引导学生分析例题，将物理问题转化为数学问题，解题过程由学生在学案上书写，然后投影，师生共同点评、总结用定义证明函数为增（减）函数的基本步骤．

设计意图：利用单调性证明物理学中的玻意耳定律，学生感受到函数单调性的初步应用；在教师引导下，学生熟悉用定义证明函数为增（减）函数的基本步骤．

师生活动：学生讨论，代表发言．

设计意图：通过数形结合思想的运用，加深对单调性定义的理解，强调：（1）单调性是对定义域内某个区间而言的，因此谈单调性离不开区间；（2）定义中的“任意”是关键；（3）函数在定义域内的两个区间A、B上都是增（或减）函数，不能武断认为函数在A∪B上也是增（或减）函数．

A.1B.2C.3D.4

师：非常好.如果f（x）在区间［1，+∞）上是单调递增的，那么f（2）＞f（1）肯定成立，可以缩小k的范围，这也是我们解决选择题很有效的方法，可以提高准确率.

师（追问）：反过来对吗？如果f（2）＞f（1），能否说f（x）在区间［1，+∞）上是单调递增的？

生：不行.

师：还有没其他的方法解决这个问题？

生：利用单调性的定义.（略）

设计意图：进一步加深对函数单调性定义的理解和熟悉用定义证明函数为增（减）函数的基本步骤．

4.回顾反思，深化新知

问题5：通过本节课学习，你有哪些收获？

师生活动：学生交流在本节课学习中的体会、收获，交流学习过程中的体验和感受，教师梳理、概括本节课主要的学习内容，并揭示蕴含的数学思想方法．

设计意图：使学生深切体会到本节课的主要内容和思想方法．

二、教学反思

中学数学对单调性的认识是“螺旋式上升”的：图像直观（直观化定义）——文字描述（描述性定义）——符号表达（形式化定义）——精准刻画（导函数定义）.本节课处在最关键环节，其难点是如何突破用静态的数学符号刻画动态的函数变化趋势，其中“任意”一词是最大的难点.我们思考以下几个问题：

（1）为什么要学习函数单调性的形式定义？（回答学习的必要性）

（2）为什么非要从左向右看？（遵循x轴正方向）

（3）怎样用数学符号语言描述自变量x逐渐增大？（抽象出x1＜x2）

（4）能否检验几个具体数值甚至无数个数值判断函数单调递增？（几何画板验证）

（5）如何做到取遍所有的x值？（逼出任意性）

（6）怎么用数学符号描述因变量y随x的增大而增大？（当x1＜x2时都有f（x1）＜f（x2））

围绕上述问题，我们采取递进式问题串的形式组织学习材料，分散难点，并寻找已有的认知经验，使得函数单调性的形式化定义水到渠成.

数学的本质是思维对话，即师生对话（引导）、生生对话（讨论）、生本对话（自学）.对话教学的关键是既关注预设的问题，又重视生成的问题.从预设与生成的角度看，本节课做得较好的地方有：（1）在学生回答了f（x）=x2的单调性后，笔者课前的预设是借助双钩函数的图像使学生产生认知冲突，让学生意识到仅仅从形上认识单调性还是不够的，还得从数的角度进一步去认识它，即学习符号化定义的必要性.没想到学生会回答“同学画的是区间［－3，3］上的图像，只能看出［－3，3］上的单调性”，这完全出乎笔者的意料，这时笔者只能将他的话重复一遍给自己留思考的时间.怎么保证x＞3时图像是一直上升的，不会下降呢？得从数的角度去分析，笔者突然意识到这不就是自己想要的吗？让学生产生认知冲突，从形上认识单调性还是不够的，还得从数的角度进一步去认识它，进而意识到学习符号化定义的必要性，于是笔者也就没必要请出双钩函数了.（2）在变式2中，笔者的预设是学生利用定义去完成，从而得到进一步加深对函数单调性定义的理解效果.令笔者始料未及的是学生利用即k＜2就得到选项，笔者意识到这不就是解决选择题，提高准确率的常用手段吗？于是很肯定地表扬了他.在教学中，教师应根据学生所答、所问及时改变预设的程序，创造性地组织教学，这既是对学生发现的肯定，更是尊重学生的表现.这样的教学真正使学生成为了学习的主人，反映了课堂教学的真实、自然.

李邦河院士曾告诫我们“数学根本上是玩概念的”.那么，如何在教学实践中“玩概念”？可谓见仁见智.章建跃先生认为，数学中“玩概念”包含两个方面：一是定义概念，二是利用概念研究数学规律.在数学概念的教学中，最忌讳的是“重结果，轻过程”，忽视学生在探索过程中的主体地位，匆忙地抛出概念，紧接着讲解各种题型及大量训练，学生不知其所以然，更谈不上发展思维了.教师应该让学生弄清概念的来龙去脉，理解概念的内涵和外延，掌握概念的应用，并且在概念的生成中，体验过程，学习方法，领悟思维，发展思维.

参考文献：

1.普通高中课程标准实验教科书（人教A版）数学（必修1）［M］.北京：人民教育出版社，2005.

2.匡宗春.关于高中数学概念的生成过程的探索［J］.数学通讯，2011（10）.

3.董入兴.对数学“构建自己的理解”的实践与思考［J］.数学通讯，2013（1）.F