在直观中抽象在抽象中建模———特级教师王岚《认识小数》教学片断赏析

孙平

“全国苏教版小学数学教材第五届优秀课评比暨课堂教学观摩会”在南京落下帷幕。其中特级教师王岚执教的三年级下册《认识小数》这节课让学生和听课老师感受到了数形结合的精妙绝伦。现撷取课中的两个精彩片断，细细品味，与读者共同分享。

片断一：在直观中抽象小数的意义

师：王老师在超市的购物中，也跟小数打起了交道。

课件出示：

师：这个购物袋要多少钱？

生：零点一元。（教师板书零点一元）

师：王老师要准备好钱去付给营业员，要准备多少钱？

生：王老师应该准备1角人民币。

师：我发现你们特别有生活经验，王老师只要准备1角人民币就可以付这个0.1元，是不是？

师：刚才你们已经把这个小数读得非常流利，如果王老师想把这个价格写下来，有没有会写的？

（学生说，教师板书0.1元）

师：把这张正方形纸看作1元，我要在这张正方形纸上分一分、涂一涂表示出0.1元，你有办法吗？

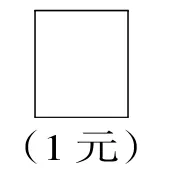
师：（学生举手）已经有这么多同学有思考了，在小组里聊一聊你准备怎么办呢？

师：借助于我们的直尺好朋友分一分、涂一涂，表示出0.1元。

师：我特别欣赏有些小组的同学，为了表示得很精确，在量的过程中，还做好了记号。

（学生操作，教师巡视指导）

师：（呈现学生的三幅作品）老师发现有的同学眼睛特别亮，在仔细观察的过程中，大家发现这几位同学的作品不完全一样，有没有什么相同的地方？

生：他们都是把1元平均分成了10份，其中的一份就是0.1元。

师：这三位同学的想法其实是一致的，都想把这些正方形平均分成10份，表示出这样的1份。听着听着怎么觉得这个新的数和我们的老朋友挂上钩了，这老朋友是谁啊？

师：我们表达的就是元，所以我们几位同学才英雄所见略同，都把这个正方形平均分成了10份，表示了这样的一份。

师：看来在这个表达的过程中，我们一下子就从新朋友又联系到了老朋友。

师：接下来，我们继续往下思考，在超市里还有其他物品也能找到他们的关系。

出示：

师：如果用这个正方形还是表示1元，这支铅笔的价格你准备怎么表示？

生：把1元平均分成了10份，涂其中的七份。

……

生：自然数1。

师：在这样的过程中，我们的同学们不仅学会了分，学会了数，还学会了找关系。

出示：

师：笔记本的价格是多少呢？这个正方形还是表示1元。

生：……

师：王老师想买的文具盒7.5元，如果用画图的方式来表达，你觉得可以怎么画呢？用一个正方形表示1元。

【赏析：三年级学生以直观形象思维为主，抽象思维在很大的程度上需要形象或表象的支撑。小数的意义十分之几就是零点几，对三年级学生来说比较抽象，难以理解。王老师为了化解这个难点，就借助于“正方形表示1元”这个载体，让学生分一分、涂一涂表示0.1元的同时，先找到了老朋友元，突出新知识的生长点后，教师顺势介绍元就是0.1元，紧接着让学生借助这样一个表象，表示出0.7元，进而再追问“还是这个正方形，你还能找到哪些老朋友和小数？”在学生找的过程中，既构建了小数与分数的联系，又直观地理解了一位小数的意义——十分之几表示零点几。即使教学整数部分不是0的一位小数时，王老师也是借助正方形这个直观图让学生根据直观图写小数及根据小数画直观图等活动来充分感知一位小数的意义。】

片断二：在抽象中建立意义的模型

师：在这个正方形里，找到了哪些十分之几的老朋友和零点几的新朋友？

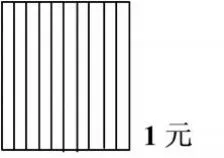
生：……

（课件演示把正方形变成长方形）

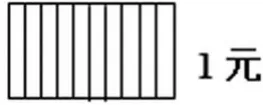
师：现在还能到找十分之几和零点几吗？如果能，很自信地告诉我。

生：能。

师：找一个。

生：……

（课件演示把长方形变成尺形）

师：还能吗？现在特别觉得像我们平时用的？

生：尺。

师：如果王老师把它看作一根米尺，那它就是1米了（课件把1元改成1米）。在这个1米的米尺上你还能找到分数和小数吗？

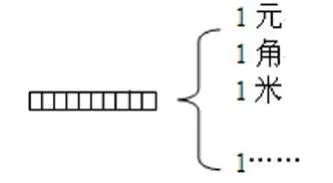
师：它除了表示1元、1米，还可以表示1（）？

生：1吨。

生：1千克。

师：如果把这个直条看作1元、1角、1米等等，它就跟一个数密切相关，这个数就是自然数1。

师：在这个线段上，你还能找到分数和小数吗？

……

师：这根调皮的线段又开始忙开了，它向两边伸展，变成了一根数轴。

师：在这个数轴上，你还能找到哪些分数和小数呢？

【赏析：《数学课程标准（2011版）》明确指出：“模型思想的建立是学生体会和理解数学与外部世界联系的基本途径。”为了帮助学生深入理解一位小数的意义，王老师是循序渐进地帮学生建立小数意义的模型，使学生悄无声息地感受到模型思想的力量。上述片断中，学生借助于正方形这个“面”直观抽象出一位小数的意义后，为了让学生的表象不仅仅停留在“面”上，王老师就借助于多媒体课件的直观演示，把这个正方形逐渐抽象成尺形。在把表示一元的正方形抽象成表示一元的尺形的过程中，学生很自然地感悟到这个尺形既可以表示1元，还可以表示1米。紧接着王老师适时地追问：“还可以表示1什么？”，这时学生对小数意义的理解，范围已逐渐扩大：任何表示具体的1（）的图形，只要平均分成十份，其中的十分之几就是零点几。教学至此，王老师并没有“罢休”，继续借助于多媒体课件，把尺形又抽象成了一条线段，让学生在线段上找小数，学生从找“面”上的小数过渡到找“线”上的小数，对学生的思维跨度看似很大，要求很高，不过在课件动态地把“面”抽象成“线”的帮助下，学生找“线”上的小数就已经顺理成章了。在这样巧妙的图形抽象过程中，润物无声地帮学生建立了一位小数意义的模型：把任何表示“1”的事物平均分成十份，其中的十分之几就是零点几。】