巧借数轴 演绎精彩——《把假分数化成整数或带分数》教学实践与思考

徐　锋

【课前思考】

《把假分数化成整数或带分数》是苏教版五年级下册的教学内容。通常，教师直接呈现例7，让学生把提供的假分数化成整数，进而交流能化成整数的假分数分子与分母的关系和化的方法。接着引出带分数，介绍带分数的意义，示范带分数的读、写。最后，通过例8，教学把假分数化成带分数的方法。整个过程，总体还比较顺畅，但对学生来说，这样的认知活动似乎理性有余而趣味不足，没法调动学生的参与热情，也正因为学习主动性的缺失，所以教学这一内容时，学生虽能掌握将假分数化成带分数的算法，但对算理的理解却往往不够到位，建立的表象也不够清晰，感悟数学思想、积累数学经验等多元目标更是成为空谈，课堂气氛也往往比较沉闷。

【教学片断】

【活动一】

(独立解答后，投影交流)

师：那谁能用一句话概括，怎样的分数在数轴上也在整数1的位置？

生：分子和分母相等的分数。

【活动二】

先观察，再从下列4个分数中任选一个在作业纸第2条数线中表示出它的位置，比比谁找得最快！

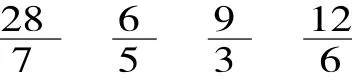
独立解答，全班交流，让学生说说想法。

师：看来你们都很聪明，挺会找巧。那请同学们继续思考：

（1）能化成整数的假分数，它们的分子和分母有什么关系？

（2）可以怎样将这样的假分数化成整数？

【活动三】

师：通过刚才的学习，我们不仅知道分子是分母倍数的假分数可以化成整数，而且还掌握了将它们化成整数的方法。

学生独立解答，组织交流：

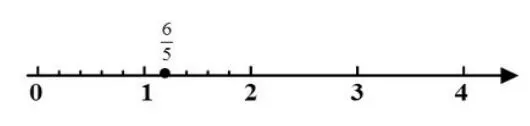
（图 2）

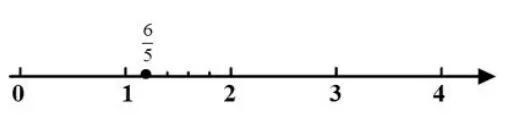
（图 3）

师：（投影图2）先请第1位同学来说说他的想法。生：我是根据的意义来找的，就是把整数1平均分成5份，表示这样的6份。

师：再来看这位同学的找法（投影图3），他找对了吗？为什么他只把第2段平均分成了5份就行了呢？生：里有6个，而5个正好是1，所以只要直接在1后面表示出剩下的那1个就可以了。

师：两种方法都可以，你们觉得哪种方法比较方便？

生：当然是第二种啦！

【活动四】

师：像6那样，分子不是分

5母倍数的假分数可以化成带分数。想一想，怎样把11也化成

4带分数？出示例8：怎样把11化成4带分数？

（可以直接思考，也可以借助作业纸上第4条数轴，先画一画，再观察）

独立解答后，同桌互说思路，全班组织交流。

投影学生作业纸：

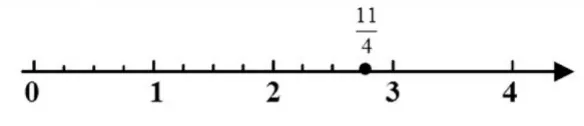
（图 4）

师：能具体说说，你是怎么想的吗？

师：看来要想理解这种方法，还不太容易，当理解有困难时，我们可以借助图来思考。（板书：11÷4=2……3），谁能结合图来说说（观察图4），这儿的“11”、“4”、“2”和“3”分别表示什么？

独立解答后，交流思考过程。

回顾反思，总结归纳。

师：刚刚我们一起研究了把假分数化成整数或带分数，回顾刚才的学习过程，想一想：

（1）什么情况下，假分数可以化成整数？什么情况下可以化成带分数？

（2）怎样把假分数化成整数或带分数？

（3）在研究把假分数化成整数或带分数的过程中，我们可以借助什么帮助我们思考和理解。

独立思考，小组讨论，全班交流。

……

【课后思考】

1.在自然优化中，主动建构新知。

以上片断，围绕“数轴”先后展开了四次活动：第一次，表示“”，通过操作、交流、比较，

2.在数形结合中，深度理解算理。

本课学习的难点就在于理解假分数化成带分数的算理。一般的教学中，学生虽能很好地掌握以上知识、技能，但很多学生对于为什么把分子除以分母的商作整数部分，为什么把余数作分子，分母为什么不变等问题，却大多说不上来。我们知道，五年级学生的思维正处于具体运算阶段，此时还需要以具体事物的表象作支撑，因此在学习把假分数化成带分数这一相对复杂的抽象算法中，必须以“形”为依托，通过形象直观的东西让学生获得丰富的表象，进而让学生的思维能顺利过渡到抽象的层面。而本例中，笔者巧借数轴，以“在数轴上表示分数”为主线组织教学，让学生在相似的问题情境中进行探究，逐层体验。学生在方法优化的过程中，感受着将假分数化成整数或带分数思考的价值，同时也不断积累着“以形助数”的经验，这样，当后面学生的理解面临真实困难时，教师只要稍作启发，学生就能自发想到“借助图来思考”，也正是在这样一种积极的学习情绪中，学生亲身经历、体验着数形结合的全过程，脑中真正建立起“数”和“形”的联系，看到算式就联想到图形，看到图形就能联想到算式，从而也真正达到了对算理的深度理解和对算法的准确掌握。

3.在数学思考中，有效积累经验。

上例中，笔者基于学生经验，创设“在数轴上表示分数”的活动情境，激发了学生的活动动机，调动起学生已有的知识经验，促使他们积极主动地参与到数学活动中，接着引导学生经历探究性数学活动的过程，通过行为操作、数学思维，在探索和交流中逐步优化数轴上表示假分数的方法，理解将假分数化成整数或带分数的算理。在这一层层递进的探究性数学活动中，学生经历了既有外显的数轴操作又有内隐的思维层面的探究活动，一方面积累了在数轴上表示分数时，将其化成整数或带分数来思考比较方便的操作经验，同时也积累了在认识数、研究数的关系时，可以借助数轴直观理解这一重要的思维经验。这一经验将在后面学习分数大小的比较，分数、小数和百分数的等值关系，尤其是感受分数的稠密性（即任意两个分数中间存在无限多个分数）等知识时被提取，经过这样长期的、层次化的过程，学生的数学活动经验就有可能逐步丰富、不断提升。