让学生在“做、议、思”中建构弧度制概念
让学生在“做、议、思”中建构弧度制概念
王琳
(山东省青岛市职教教研室,266023)
弧度制是学生学习三角函数知识中的一个难点,部分学生往往在这个拦路虎面前“缴械投降”,以致影响后续阶段的高中数学学习.巧设实验,让学生在“做、议、思”中建构弧度制概念的课堂教学实践,打破了“纸上谈兵、空手论剑”的教学常态,让学生从弧度制学习的困境中走了出来.
问题1为什么要学习弧度制?
角度制是刻画角大小的一种度量制,为何还要学习弧度制呢?可作如下教学设计:
情境1姚明身高2.26米,姚明身高7.41英尺,同样是姚明的身高,两组数据为何不同呢?
设计目的以我国著名篮球运动员姚明的身高为例,进行生活化的情境设置,说明度量长度有多种方法,从而引申出角的度量也有不同的方法.
情境2视频演示工具万能角度尺的使用(见图1),说明我们之前度量角的方法是角度制,而弯曲件的测量与加工(见图2),则从另一个角度说明引入弧度制的必要性.
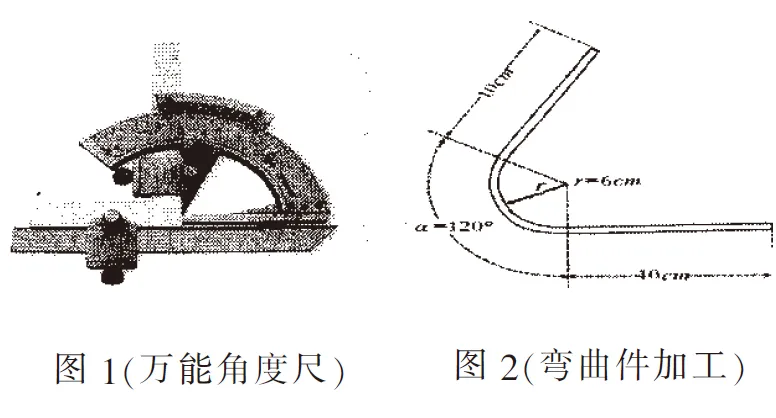
设计目的解决现实生活中的实际问题,有必要引入角的另一种度量方法——弧度制.
问题2弧度制的基本度量单位是如何规定的?
1弧度角的含义是建立弧度制概念的关键.我们把等于半径长的圆弧长所对的圆心角叫做1弧度的角.数学教学中常采用下定义的教学方式,但学生的学习效果往往并不理想.这里,可设计如下实验:
实验准备学生每人准备一大一小两张圆形卡纸(半径自定),一根无弹性的白棉线等.
实验1(1)请学生在一张圆形卡纸上作出900的角(以圆心为顶点);
(2)提出问题:如何在卡纸上作出10的角?动手画出来.
实验2(1)指导学生阅读教材中对1弧度角的概念的描述;
(2)让学生自主探究,如何在圆形卡纸上作出1弧度的角;
(3)以小组为单位,相互交流1弧度角的画法;
(4)学生归纳总结:什么叫1弧度的角——等于半径长的圆弧所对的圆心角叫做1弧度的角.
设计目的通过两组实验,让学生动手操作,在做中感知、理解1弧度的角的概念.
问题3圆心角的弧度数和半径有关吗?
1弧度角的概念已初步建立,根据概念描述学生可能还会有所疑惑,角的弧度数是否与半径有关?可设计如下实验:
实验3(1)请学生在大小两张圆形卡纸上分别作出1弧度的角;
(2)观察、比较所作两个角的大小;
(3)小组合作交流,说一说发现的结论.
设计目的通过比较大圆和小圆中所作的1弧度角的大小,让学生在做中悟,做中辩,体会到圆心角的弧度数是不随半径的变化而变化的;同时,为实验4的实施埋下了伏笔.
实验4(1)学生根据1弧度的角的概念,在圆形卡纸上分别作出2弧度、3弧度、1.5弧度的角,并完成如下实验报告.
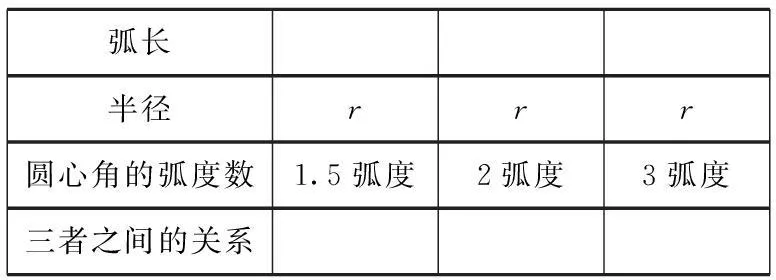
弧长半径rrr圆心角的弧度数1.5弧度2弧度3弧度三者之间的关系
(2)学生通过实验报告,总结出公式:
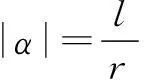
设计目的让学生在完成实验的过程中感知弧长、半径、圆心角的弧度数三者之间的关系,为后面进行角度与弧度的互化奠定坚实的基础.
问题4弧度制与角度制之间的关系?
角度制和弧度制都是刻画角的大小的度量制,前者的基本度量单位是度,后者是弧度.二者之间有什么关系呢?可设置问题情境引导学生找到它们之间的换算关系.设置题组如下:
已知圆的半径是r.
(1)计算圆的周长=______,由此得出圆周角的弧度数=______;
(2)圆周角的度数=______;
(3)得出结论:360°=______(填弧度数);即180°=______(填弧度数);
1弧度的角大约等于______(填角度数).
层层设置的实验,实现了让学生在做中学、做中悟、做中议、做中思,深刻理解弧度制概念的目的,为学生学习三角函数打下了良好的基础.

