高考数学中参数方程的应用举例
高考数学中参数方程的应用举例
杨志涛
(陕西省西安市惠安中学,710302)
从目前参加新课标高考的省份对参数方程与极坐标内容的考查来看,主要考查极坐标方程和直角坐标方程的互化及常见曲线的极坐标方程与极坐标方程的简单应用.预测2016年高考在试题难度、知识点考查等方面,不会有太大的变化.针对考查直线、圆和圆锥曲线的参数方程以及简单的应用问题,复习这部分内容时,应紧紧抓住直线的参数方程、圆的参数方程、圆锥曲线的参数方程的建立以及各参数方程中参数的几何意义,同时要熟练掌握参数方程与普通方程互化的一些方法.
考纲对本版块知识要求:
(1) 了解参数方程,了解参数的意义;
(2) 能选择适当的参数写出直线、圆和椭圆的参数方程.
高中数学中,参数方程的知识点包括以下几方面:
1.参数方程的概念
在平面直角坐标系中,如果曲线上任意一点的坐标x、y都是某个变数t的函数
(*)
并且对于t的每一个允许值,由方程组(*)所确定的点M(x,y)都在这条曲线上,则方程组(*)就叫做这条曲线的参数方程,变数t叫做参数.
2.直线的参数方程
过点M(x0,y0),倾斜角为α的直线l的参数方程为
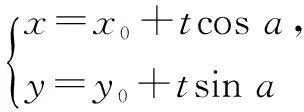

3.圆的参数方程
(1)圆心在原点、半径为r的圆的参数方程为

(2)圆心为C(a,b),半径为r的圆的参数方程为

4.常见曲线的参数方程的一般形式


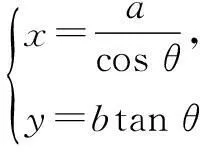
(3)抛物线y2=2px(p>0)的参数方程为
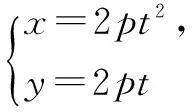
5.参数方程和普通方程的互化
把参数方程化为普通方程,需要根据其结构特征,选取适当的消参方法.常见的消参方法有:代入消参法;加减消参法;平方和(差)消参法;乘法消参法等.
把曲线C的普通方程F(x,y)=0化为参数方程的关键:一是适当选取参数;二是确保互化前后方程的等价性.
典型应用1参数方程与普通方程的互化
例1把下列参数方程化为普通方程:

思路(1)利用平方关系消参数θ;
(2)代入消元法消去t.
代入三角恒等式cos2θ+sin2θ=1,得(x-3)2+(y-2)2=1,这就是它的普通方程.
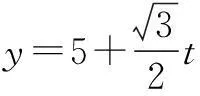
评注化参数方程为普通方程的基本思路是消去参数,常用的消参方法有代入消去法、加减消去法、恒等式(三角的或代数的)消去法.参数方程通过代入消元或加减消元消去参数化为普通方程,不要忘了参数的范围.

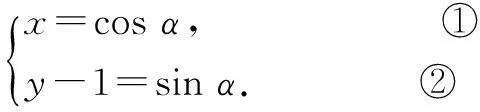
①2+②2,得x2+(y-1)2=1,
答案:x2+(y-1)2=1.
典型应用2直线与圆的参数方程的应用


(2)当直线l与圆C有公共点时,求α的取值范围.
思路(1)求圆心到直线l的距离,这个距离减去圆的半径即为所求;(2)把圆的参数方程化为直角坐标方程,将直线的参数方程代入得关于参数t的一元二次方程,这个方程的Δ≥0.


评注如果问题中的方程都是参数方程,那就要至少把其中的一个化为直角坐标方程.




典型应用3圆锥曲线参数方程的应用
思路把直线方程用参数表示,直接与椭圆联立,利用根与系数的关系及弦长公式可解决.
解由条件可知直线的参数方程是

代入椭圆方程,可得

设方程的两实根分别为t1、t2,则由二次方程的根与系数的关系,可得

则直线截椭圆的弦长是

评注普通方程化为参数方程:化普通方程为参数方程的基本思路是引入参数,即选定合适的参数t,先确定一个关系x=f(t)(或y=φ(t)),再代入普通方程F(x,y)=0,求得另一关系y=φ(t)(或x=f(t)).一般地,常选择的参数有角、有向线段的数量、斜率,某一点的横坐标(或纵坐标).普通方程化为参数方程需要引入参数,选择的参数不同,所得的参数方程也不一样.

直线的参数方程为


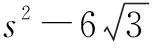
设A、B对应的参数分别为s1,s2,则



从近两年的新课标高考试题可以看出,对参数方程的考查重点是直线的参数方程、圆的参数方程和圆锥曲线的参数方程的简单应用,特别是利用参数方程解决弦长和最值等问题,题型为填空题和解答题.很多自主命题的省份在选考坐标系与参数方程中的命题中多以综合题的形式命题,而且通常将极坐标方程、参数方程相结合,以考查考生的转化与化归的能力.只要我们认真钻研新课标,用心教学,一定会取得好的成绩.

