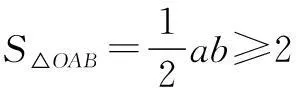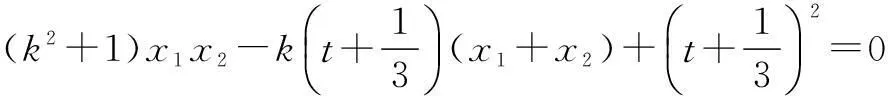实现高三数学高效复习的三个着力点
实现高三数学高效复习的三个着力点
刘起鹏
(江苏省南京市溧水区第三高级中学,211200)
高三阶段数学复习的主要任务是查漏补缺、提升学生的数学应用能力.教学中出现频率较高的课型是习题课,教师精选题目,学生课前自主练习、课上交流探讨互动、课后巩固总结.但是在实际教学中,这样的习题讲评课往往教学目标不明确.教师一讲到底,难有学生的参与和互动;教师就题论题,缺乏对问题的深入探究;教师讲完了事,缺少方法的思考和总结.这种流于形式的习题讲评,不能引起学生思维的共鸣,学生遇到类似的问题还是无从下手.如何改变提高复习课的效率呢?笔者认为应从挖掘课本知识,发挥一题多解与多解归一在复习中的作用及注重学生的解后反思这三个方面入手,追求高效的复习教学.
一、挖掘课本知识,通过现象看本质
新课程强调要用好、用活教材,课堂上,教师要充分挖掘教材的内涵和外延,提高解题技能.在复习解析几何中的斜率时,要充分理解斜率公式就会在解决一些题目时取得事半功倍的效果.
案例1已知a,b,m均为正数,且a 对于新学解析几何知识,教师如果不再提炼、运用,学生就不能灵活应用于解题中.在其他章节知识学习时,重温已学过知识的来源与推导,学生往往会有“恍然大悟”的感觉,不但可以巩固这些公式,而且也能领会其中所体现的方法、思想,解题时就可快速、高效. 二、发挥“一题多解”与“多解归一”的作用 “一题多解”是采用多种解题方法解决同一个数学问题的教学方法,是培养思维多样性的一种重要途径,它有利于培养学生辨证思维能力,加深对概念、规律的理解和应用,提高学生的应变能力,启迪学生的发散性思维.“多题归一”是在复习时,将很多例题有机地串联起来,编成一组,引导学生进行观察,引导学生对多题一解进行反思,可提高学生的化归能力,使零碎的知识成为一个有机的整体,体会通性通法在解题中的作用,培养学生观察问题的敏感性和思维的系统性,从而提高学生的复习效率和运用知识的能力. 案例2如图2,过点P(1,1)作直线AB,分别与x轴的正半轴、y轴的正半轴交于点A、B,当直线AB在什么位置时,∆AOB的面积最小?最小面积是多少? 此题入口宽,方法多样,可以引导学生从各个不同的视角解决问题. 当且仅当a=2时等号成立,此时b=2,下同解法1. 解法3(运用整体代换)同解法1,可得 ① 下同解法1. 解法4(运用导数)同解法2,得 令S′(a)=0得a=2(a=0舍弃). 当0 由上述讨论可知S(a)在a=2时取得最小值. 此时直线方程为x+y-2=0,即当直线AB方程为x+y-2=0,∆AOB的面积最小值是2. 解法5(柯西不等式视角)同解法3,得 故当a=b=2时,S∆OAB取最小值2. 解法6(运用向量数量积)同解法3,得 由m·n≤|m||n|,得 下同解法1. 此时a=sec2α=2,b=csc2α=2,即当a=b=2时,∆OAB的面积最小为2,此时直线方程为x+y-2=0. 三、注重解后反思,渗透数学思想 高三阶段尤其到了中后阶段的综合题考察知识点多、能力要求高,就题论题的讲解效果不好.诚如玻利亚所言:“一个好的教师应该懂得,而且使他的学生也懂得,没有一个问题一经解决就算是完全做完了.一个问题解决之后,常常还留下一些事情可做:经过充分的研究和观察,我们可以改善解答;而在任何情况下,总能增进我们对解答的了解.”在解题后引导学生反思、总结,能使学生掌握一类问题的一般解题方法,能够提升对数学思想方法的理解,真正找到解题的“金钥匙”. 这道题目综合性强、思维要求高,不少学生因为方法不得当或缺乏运算能力,不能做出准确的解答.笔者在教学这道题时,让学生自主补充、完善整个解题过程,并对该题进行了解题反思. 生1:若直线l⊥x轴,交椭圆于短轴端点,以AB为直径的圆显然过定点T(0,1); 下面我就不会做了. 师:还不错,能考虑到直线斜率不存在的讨论.还有同学补充吗? x1x2+(y1-1)(y2-1)=0, 代入即可证出. 如果课堂讲解就此止步,学生再次遇到类似的问题,还是很难形成较为顺畅的解题思路.因此,完成解题后,教师带领学生继续深入思考就显得尤为重要. 师:把几何定点问题转化为代数等式恒成立问题,解题思路很清晰,但要求学生有较强的运算能力,感兴趣的同学课后可以按此方法继续完成解答.能不能先找到这个定点T,再证明正确性呢? 生4:我取特殊直线,当l斜率不存在时,交y轴于点(0,1)和(0,-1),因此定点为T(0,1)和T(0,-1).但原题只有T(0,1),好像不对? 师:取特殊直线先得到定点,必要时可多取几条.找到定点,再证明正确性.这种由特殊到一般数学思想方法能大大降低解题的难度.同学们进一步思考下面的问题: 先找定点,再证明其正确性,能够明确运算目标,并且降低运算量,这种方法更适合学生的思维方式. 对于较综合的题目,学生往往难以真正体会蕴藏其中的数学思想,因此学生解题后还需进一步的反思.为深入理解“由特殊到一般”的数学思想,学生可进一步思考. 生:设M(m,0),取特殊直线. 师:可否考虑点P无限趋近于点O的特殊情形呢? 师:方法中蕴含了极限思想,请大家继续完成本题. 教师引导下的总结和反思,是将学生掌握的思想方法进行升华,内化为能力的过程.在高三数学复习中,学生需要进一步提升自己的思维能力,因此教师解题后需要引导学生反思,优化解题方法,渗透数学思想. 高三数学复习应多给学生更多自我完善和自我探索的空间,多一些发展学生思维、锻炼学生能力的活动和环节,少一些教师想当然的讲解.高中课程标准中指出“教学中,应鼓励学生积极参与教学活动;既要有教师的讲授和指导,也要有学生的自主探索与合作交流;教师要创设适当的问题情境,鼓励学生发现问题解决的途径.”在习题讲评课中注重学生的参与、注重对问题的变式拓展、注重解题后反思,会大大提高专题讲评课的效率. ○高考复习研究○