求函数值域的常用方法
求函数值域的常用方法
姚源信
(广西凌云县中学,533000)
函数的值域是函数构成的三大要素之一,它可以由定义域和对应法则来确定.函数的值域,既能从全局上反映函数的性质,又能从局部上体现函数值的变化规律,是函数定义中重要的必不可少的组成部分.
求函数的值域是常考题型.在许多问题,特别是实际问题(应用题)中,经常遇到求某个量取值范围或最大值、最小值的问题,实际上都是求函数的值域.因此,我们有必要专门探讨求函数的值域的方法,将之分门别类,应用于教学实践,提高学生对这一问题的认识和解决值域问题的能力.以下是本人结合多年的教学实践,总结的一些关于求函数值域的方法,仅供大家参考.
一、单调性法
求函数值域可以利用单调性的定义、复合函数的单调性法则和导数等相关知识确定函数在某个区间(该区间为定义域的子集)的单调性,再用单调性求出函数在该区间上的值域.



故所求函数的值域为[2,+∞).
二、配方法
配方法主要用于求二次函数的值域问题.配方的方法是:先考虑二次项的系数,将二次项系数变为1,再取一次项系数的一半进行配方,注意取适当的常数项以便保证整个过程是恒等变形.
例2求函数y=2x2-4x+3(x∈R)的值域.
解y=2x2-4x+3
=2(x2-2x)+3
=2(x-1)2+1,
易知y≥1.
故所求函数的值域为[1,+∞).
三、换元法
若一个函数通过换元的方法可以化简成常见的初等函数,则可以用初等函数的性质来求函数的值域.换元的方法主要有代数换元法和三角换元法,换元时要注意所换元的范围.
例3求函数y=4x-6×2x+1,x∈(2,3)的值域.
解令t=2x,则4x=t2,且x∈(2,3)时,t∈(4,9),所以
y=t2-6t+1=(t-3)2-8.
易知,当t∈(4,9)时,
ymax=(9-3)2-8=28,
ymin=(4-3)2-8=-7.
所以所求值域为[-7,28].
四、判别式法

五、反函数法
在反函数的定义中,指出反函数的定义域与原函数的值域相同,反函数的值域与原函数的定义域相同.因此,求一个函数的值域可以通过去求反函数的定义域来实现,这也是一个求值域的重要的方法.

解先求该函数的反函数,过程如下:
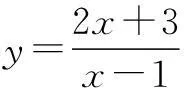
xy-y=2x+3,
互换x,y得反函数为

从而可知,反函数的定义域为
(-∞,2)∪(2,+∞).
故原函数的值域为
(-∞,2)∪(2,+∞).
六、分离常数法
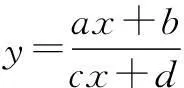
七、不等式法

解分子分母同除以x,得
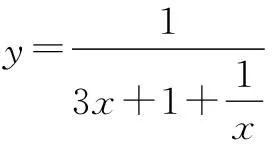
因为x>0,所以
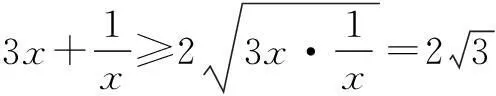

综上所述,所求函数的值域为
除了上面所列举到的七种常见的求函数值域的方法以外,常用的求函数值域的方法还有数形结合法和函数有界性法等等,这些方面与上面所列举的方法有异曲同工之妙,在此就不一一列举了.总之,熟练掌握求函数值域的方法是考试大纲的明确要求,也是高考常考的题型.广大师生应该引起足够的重视,认真开展教学研究,以达到考试大纲的要求,取得优异的成绩.

