我国小学数学教材的基本特点之四：兼收并蓄

胡重光　杨高全



我国小学数学教材的基本特点之四：兼收并蓄

胡重光杨高全

自我国的小学数学教材编写放开以来，特别是本轮课改开始之后，老师们对小学数学教材的讨论日渐热烈，各种意见越来越多。对于这些意见，教材采取了一种十分稳妥的处理方法：兼收并蓄，既编入新意见，也保留旧内容。同时，由于课标提倡算法多样化，教材也就相应地介绍了多种算法。类似这样的处理多了，也就形成了一种特点。兼收并蓄当然有它的好处，比如多介绍几种计算方法，让学生自由选择，可以适应不同学生的思维方式，培养思维的灵活性。但也要遵循几条基本原则：1.“兼收”的意见必须是正确的；2.错误的观点或方法必须被纠正或淘汰；3.不同的观点或方法如果有明显的优劣之分，则劣者不应兼收；4.不符合教学目标的方法，即使是恰当的也不应兼收，因为我们必须以有限的教学时间学习最应该学习的知识。

一、正整数加法的算理

算理是指计算的根据，它直接决定计算的方法。我国的教材原来是以数的“分与合”作为正整数加法的算理的，现在的教材仍然首先介绍“分与合”（如图1所示）。

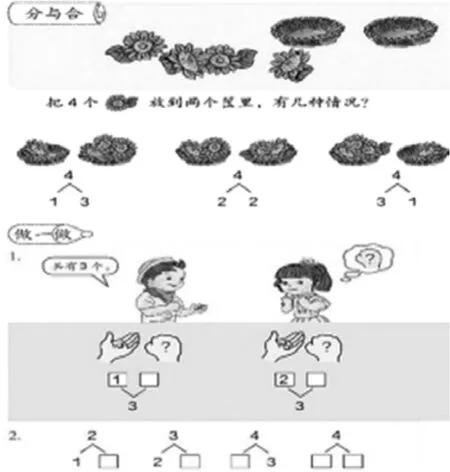
图1

在进行了一定数量的练习后，就引入相应的加法和减法。具体地说就是：

因为1和3可以合成4，所以1＋3＝4，3＋1＝4。

因为4可以分成1和3，所以4－1＝3，4－3＝1。

这一算理我们使用了多年，但是本轮课改开始以来，它受到了质疑。原因看起来很清楚：1和3可以合成4，与1＋3＝4或3＋1＝4其实是同义反复，后面两个式子也一样。

那么正确的算理是什么呢？弗赖登塔尔明确指出：“加法是向前数数，减法是向后数数。”其原理就是自然数的序数理论，并且学前儿童正是这样算数的。

在这种情况下，教材采用了如下的处理办法（如图2所示）。

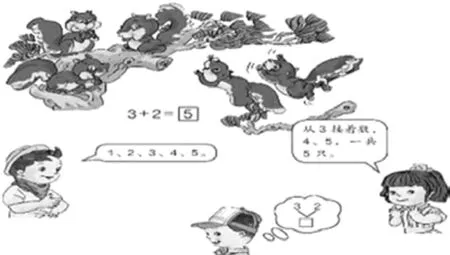
图2

图2介绍了计算3＋2的三种方法。左右两种方法都是数数，中间的方法则是数的合成。可以说这样编排充分体现了兼收并蓄的特点。

但是根据前面的三条原则，“数的合成”这种方法应当淘汰，另两种方法都是数数，而左边的方法明显比右边的复杂（特别是当数字较大时），从1数起也是不必要的，所以也不应收入。

二、整十数加整十数

整十数加整十数，看起来很简单，但也有不同方法可以兼收并蓄。（如图3所示）10＋20的两种算法中，第一种算法的道理十分清楚。它利用了计数单位来说明算理，其原理与量的计算一样：1米＋2米＝3米，1公斤＋2公斤＝3公斤……不管是什么量相加，只要单位相同，将量数相加即可。量的加法比数的加法更具体，是看得见、摸得着的，儿童在生活中多有接触，因此容易理解。如果教师结合儿童熟悉的实例进行类比教学，将收到良好的效果。第二种算法只列出了两个算式，并没有说出任何道理。我们不能说：因为1＋2＝3，所以10＋20＝30。把这种算法写在这里，难免会促使教师让学生死记硬背。

图3

三、笔算与口算

这里的“兼收并蓄”在于教材既要求学生口算，又要求学生笔算。

（一）两位数加一位数的不进位加法

这一内容安排在二年级上册（如图4所示）。

图4

这里介绍了口算和笔算两种方法。掌握两种方法是否更好呢？从例题我们可以看到，这里的不进位加法是两位数加一位数，个位不进位。对二年级学生来说，这应该是相当容易的。既然如此，就没有必要再费时费力去写竖式。如果考虑到后续学习的必要，就更应该要求学生口算了。因为三年级上册第二单元的万以内的加法中，对于35＋34和39＋44这样的加法（后一道是进位加法），是要求学生口算的，并且只介绍了口算，没有介绍笔算。熟练掌握二年级上册的口算，就可以为这里的难度较大的口算打下基础。

（二）两位数乘两位数的笔算乘法

这一内容安排在三年级下册，教材通过一道应用题学习算法。在介绍竖式计算前，先利用形象的“点子图”讲了两种思路和算法（如图5所示）。

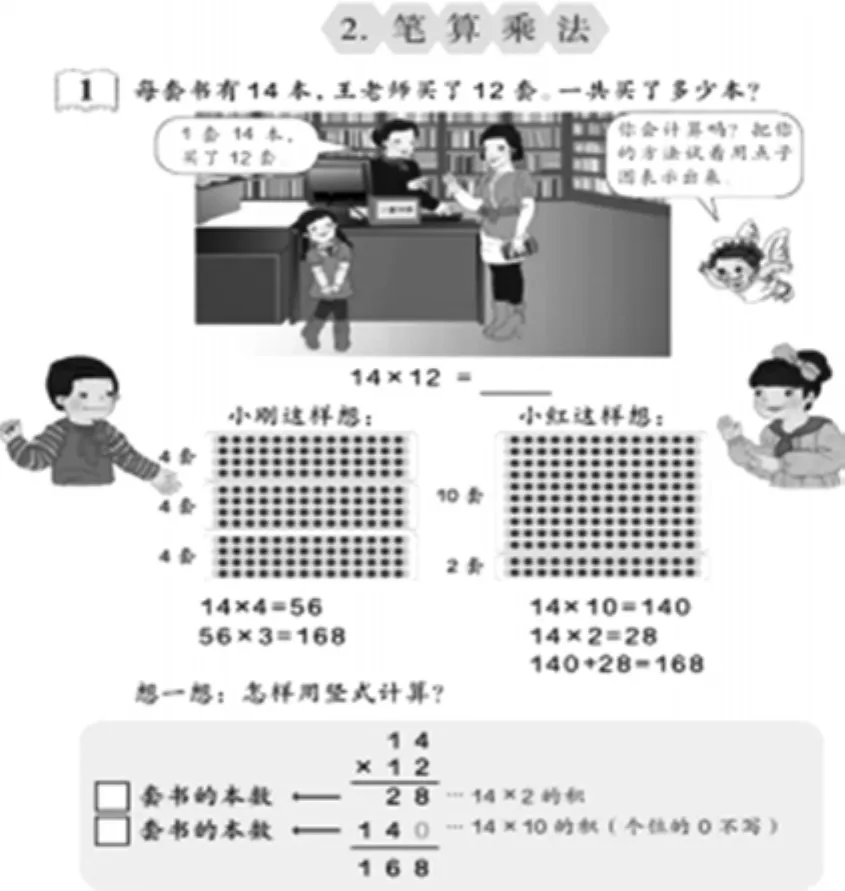
图5

右边的思路和算法与竖式笔算是一致的，可以帮助儿童理解竖式的计算原理，并且把点子图分成10套和2套两部分，可以形象地说明14×12＝14× 10＋14×2，即乘法的分配律。但是点子图是先用10乘，后用2乘，竖式是先用2乘，后用10乘，两者顺序相反。因此，点子图应改为2行的在上，10行的在下，算式也应相应地改变顺序。

左边的算法则有点奇怪：它与竖式计算毫无联系，如果说是让学生学习口算——这已与本节的教学目标不一致——也比右边的算法更难：左边要算两道进位乘法算式，而右边的两道乘法算式都不进位，并且非常简单。由此看来，教材增加这种算法，似乎只是为了体现算法多样化。

笔算和口算不能简单地看作两种计算方法，而应视为不同的教学目标。与笔算相比，口算对儿童的思维能力要求更高，也更能训练他们的思维能力。因此不应该把它们作为不同的计算方法由学生自由选择，而应该根据儿童的思维发展水平要求他们掌握其中的一种。一般来说，能口算的，应该要求学生口算。

教材中的“兼收并蓄”还有其他例子，为了兼顾系统性，本文只选讲了计算方面的例子。（本文是基金项目：湖南省教育科学规划课题（XJK013CJC004）、湖南省省级重点建设学科“课程与教学论”建设项目资助的成果之一）

（作者单位：湖南第一师范学院）

思想