一种改进的BBO算法及在热工PID优化中的应用

薛　虹,韩　璞

(华北电力大学 河北省发电过程仿真与优化控制重点实验室，河北 保定 071003)



一种改进的BBO算法及在热工PID优化中的应用

薛虹,韩璞

(华北电力大学 河北省发电过程仿真与优化控制重点实验室，河北 保定 071003)

摘要：为了提高BBO算法在热工系统PID控制器参数优化方面的性能，改善其寻优能力，给出一种改进的生物地理学优化算法。在原有的迁移操作的基础上引入粒子群优化算法的寻优策略，使整个迁移过程具备一定的方向性，同时应用淘汰策略剔除迁移突变后较差的参数。一方面方向性的迁移及淘汰机制保证其快速的寻优收敛特性，另一方面突变机制保证广域搜索的全局特性，避免陷入局部极值。将其与原BBO算法进行比较，仿真结果表明改进的BBO算法在收敛速度和收敛精度上较标准BBO算法有较大提高，应用于PID控制器参数优化是可行的。

关键词：改进BBO算法;PID参数优化；仿真研究

0引言

生物地理学优化算法(Biogeography-Based Optimization,BBO) 是以生物地理学理论为基础应用到优化问题进而产生的一种新型进化算法。其基本原理是根据栖息地之间物种迁移及变异来完成信息交换,通过种群间的迁入、迁出、变异等因素来提高栖息地的适宜度，从而得到问题的最优解[1]。该算法具备良好的收敛性及稳定性，许多学者针对这一算法做了广泛的研究，大大促进了其在工程领域中的应用：文献[2]将差分变异算法与生物地理学算法结合，将其应用于经济负荷调度问题的求解中得到了良好的效果，且明显优于基本BBO算法的求解效果。文献[3]将差分进化算法与生物地理学算法融合，将其应用于最优潮流问题的求解，并证明了该混合算法是切实有效的。文献[4]将反向学习技术(OBL)与BBO 算法相结合成功解决了图像分割问题。文献[5]将Logistic混沌映射改进原变异机制，提出了一种改进的BBO算法，并将其应用于雷达正交波形的设计中。文献[6]将模拟退火算法与BBO算法结合，提出了SA-BBO算法，并将其应用到汽轮机组最优运行初压的确定问题中。

本文将BBO算法其引入到热工系统PID控制器参数优化中，引入粒子群优化算法的寻优策略，使整个迁移过程具备一定的方向性，避免了单独采用迁移机制时仅将PID某一参数进行交换，极有可能造成新PID参数间不匹配，导致整个优化过程的收敛速度降低、优化特性变差的缺陷；同时采用淘汰机制，对每次优化后参数与原参数进行比较，性能较好的进行下一次迭代，从而保证不因迁移和突变操作而失去较优特性。这样，一方面方向性的迁移及淘汰机制保证其快速的收敛特性，另一方面突变机制保证广域搜索的全局特性，避免优化过程中陷入局部极值。

1BBO算法基本原理

BBO算法中每个群体都具有若干特征向量，描述为适宜向量(Suitable Index Vector，SIV)，特征向量SIV对应优化问题的解，其中的每一个变量相当于优化问题解向量的分量；栖息地的适宜度指数(Habitat Suitability Index, HSI )是对适宜度的向量SIV优劣的度量值,用于对群体进行评价，对应于优化问题优化目标函数值[7]。BBO算法在求解优化问题中，需随机构造多个群体X及对应的适宜度向量SIV作为优化问题的初始解，通过群体的进化，改善HSI，进而得到问题的最优解。

(1)迁移操作

BBO算法利用迁移机制完成与其它群体之间的信息交换，进而对解空间进行广域搜索，由迁入率λ和迁出率μ来影响群体迁移程度。HSI高的栖息地包含的物种多，由于其己经有接近饱和的物种数，所以其相应的物种迁出率μ较高，而物种迁入率λ较低;相反，HSI较低的群体对应的物种较少，迁入新物种的概率较高，而物种迁出概率较低，故具有较高的迁入率和较低的迁出率[8]。因此迁入率λ与迁出率μ为该群体中物种种类k的函数。根据生物地理学物种分布情况,可以得到不同的迁移率模型函数，文献[7]通过对比显示余弦函数模型具有更优越的性能，图1所示的为余弦函数模型。

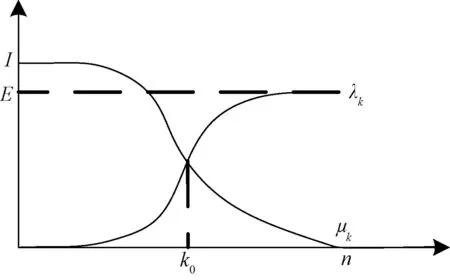
图1　迁移率余弦模型Fig.1　The cosine model of mobility

图1中，I为最大迁入率；E为最大迁出率；n为群体中的饱和时的物种数量；k0为群体平衡时的物种数。余弦函数模型中迁入率λ与迁出率μ的表达式如下：

(1)

(2)

在迁移操作过程中，BBO算法根据其迁入率λ并依据概率选择需要迁入的群体Hi;根据迁出率μ依概率选择需要迁出的群体Hj;接着从Hj中随机地选择某一特征量替代Hi中相应的特征量, 最后通过计算HSI来评价整个群体的适应度。

(2)突变操作

BBO算法采用突变操作模拟因突发事件造成群体适宜度发生变化的情况。根据群体i在种群数量为k时的概率Pk对群体的特征变量进行突变。其中Pk满足如下表达式:

(3)

根据生物地理学的基本原理[11]可知，群体的变异率与其物种概率成反比，其变异率mi为

(4)

式中：mmax为算法定义的群体最大变异率；Pmax为所有物种概率的最大值。这一突变函数可使低HSI的方案以较大概率发生突变,使之进一步的改进。

在突变操作中，依据mi选择需要修改的群体Hi，进而随机产生一个特征变量值替换Hi中对应的特征变量，进而计算新的HSI值。

2改进的BBO算法原理

2.1迁移策略的改进

将BBO算法应用到优化热工系统PID控制器参数中，PID控制器参数作为其BBO算法的特征向量，其迁移策略仅将PID参数中的某一参数进行替换，这就难以保证替换后的PID参数匹配合理，造成收敛速度慢，收敛精度差的缺陷。针对上述问题，本文将粒子群优化算法迭代搜寻最优值的优化原理[9]引入到BBO算法的迁移策略中，其改进的迁移策略原理为：依据迁入率λ确定需要改变的群体Hi，依据迁出率μ依概率选择需要迁出的群体Hj，并结合当前的搜索过程中的得到的当前最好适应度的群体Hmax，依据(5)式得到Hi的最新值

Hi(m)=Hi(m)+c1rand(1)(Hj(m)-

(5)

式中：m=1,2,…，D,D为群体特征向量SIV的个数；rand(1)为1从内的随机数。

2.2淘汰机制

为了保证每次迭代都使得PID参数往最优解的方向进化，即个PID参数的较优特性不因迁移或变异过程而变差，本文在BBO算法中引入淘汰机制，即将经迁移后的群体特征向量SIV1、突变后的特征向量SIV2、及前一次迭代后的群体特征向量SIV3三个特征向量对应的适宜度指数进行比较，选出其中适宜度指数最大的特征向量作为本次迭代该群体的特征向量。这样若前一次迭代后的特征向量对应的适宜度指数好于经迁变及迁移突变后的特征向量对应的适宜度指数较差，则淘汰此次迁移及突变的特征向量，保留原有特征向量。这样就保证了原群体中较优个体不因迁移和突变而失去较优特性，提高了算法的收敛速度，能够更快的收敛到最优解。

2.3改进BBO的PID控制器参数优化

将改进的BBO算法应用到热工系统PID控制器参数优化中，其中PID控制器的参数对应于改进BBO算法中的特征向量SIV，同时为了保证优化的控制器参数作用于系统时具备良好的定值跟踪能力、抗击内外扰动的能力，针对每一次优化的结果对系统进行定值扰动、内部扰动及外部扰动仿真试验，并以3种试验结果的误差平方和作为适宜度指数值来评价优化的优劣，误差平方和越小，其适宜度指数值越高，优化性能越好。改进BBO算法优化流程如图2所示。

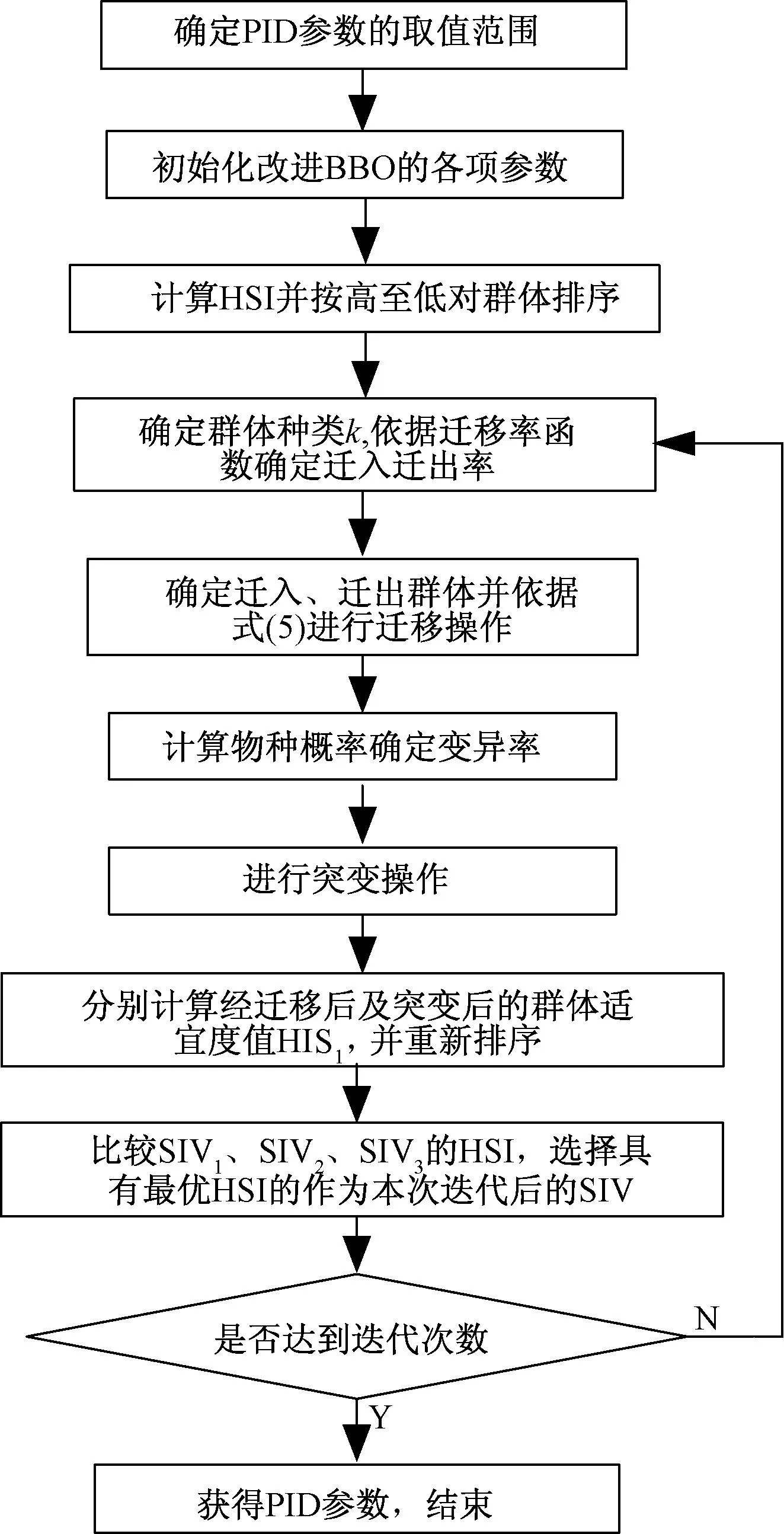
图2　BBO混合优化算法流程Fig.2　The algorithmic process of improved BBO

3仿真验证

3.1对象描述

为验证本文所提出方法的有效性，采用文献[10]中给出的某600 MW超临界直流机组，在负荷P=580 MW，再热汽温度为T=566 ℃时烟气挡板阶跃扰动下得到的再热器温度传递函数模型作为文中所提方法的PID优化控制研究对象，如式(6)所示：

(6)

3.2改进的BBO优化算法参数设置

本文中按照BBO算法参数设置原则初始化BBO参数，对于迁移率函数的选择，文献[7]中经过证明选取余弦函数模型具有更优越的性能，因此本文选取余弦函数作为迁移率函数模型。另外对于(5)式中c1、c2的取值依据粒子群算法中的参数设置原则，最终本文中改进BBO算法的主要参数设置如表1所示，其中，G为进化次数。

表1　改进BBO算法参数设置

3.3仿真研究

为了说明本文所提算法的有效性，作为对比，本文给出了一般BBO算法对(6)式中的传递函数PID控制器的参数优化，其中BBO算法的参数按照与表1相同的参数进行设置。在Matlab软件中分别采用两种算法对(6)式进行优化。限于本文篇幅有限，不失一般性的给出连续5次采用BBO及改进BBO算法进行PID优化的仿真结果，其进化次数与最小误差的优化曲线如图3所示。

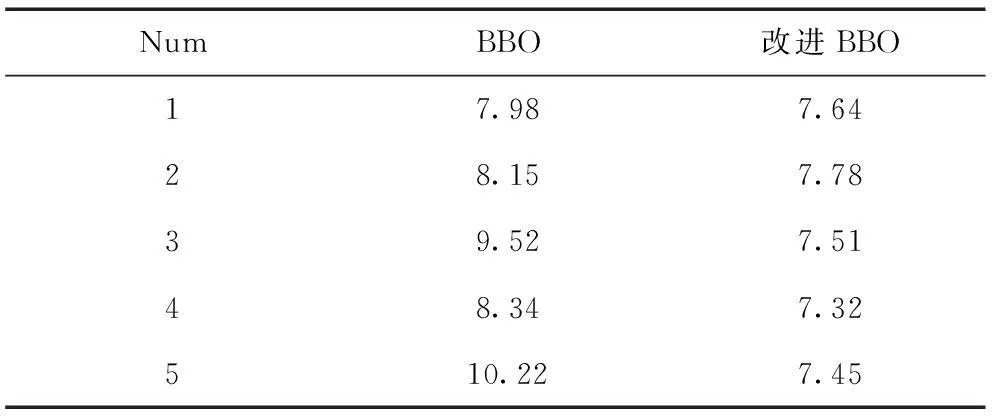
其对应的最小误差如表2所示。

综合图3与表2可以看出，在PID寻优过程中相比于BBO算法，改进BBO算法具备更快的收敛速度，并且优化结果要好于传统BBO算法。另外表2的数据可以看出，连续5次相同优化仿真结果中，BBO算法的优化结果上下浮动较大，优化结果不稳定；而改进BBO算法优化结果中最小误差均在7.5左右上下微小浮动，其方向性的收敛特性保证了历次收敛结果的快速性及稳定性，使其能够在较短的进化周期内获得满意的优化结果。

另外，为了验证优化得到的PID参数的控制效果，本文选取第3次仿真试验中获得的PID参数控制(6)式所示系统的控制中。BBO及改进BBO优化算法获得的控制器如下：

(7)

(8)

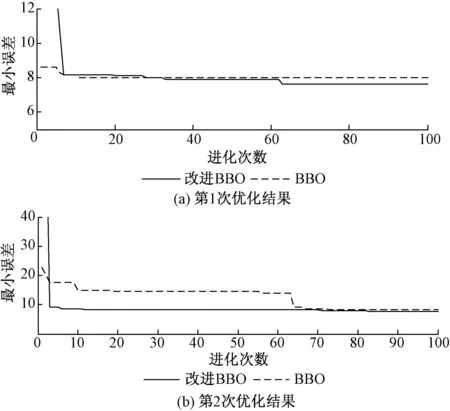
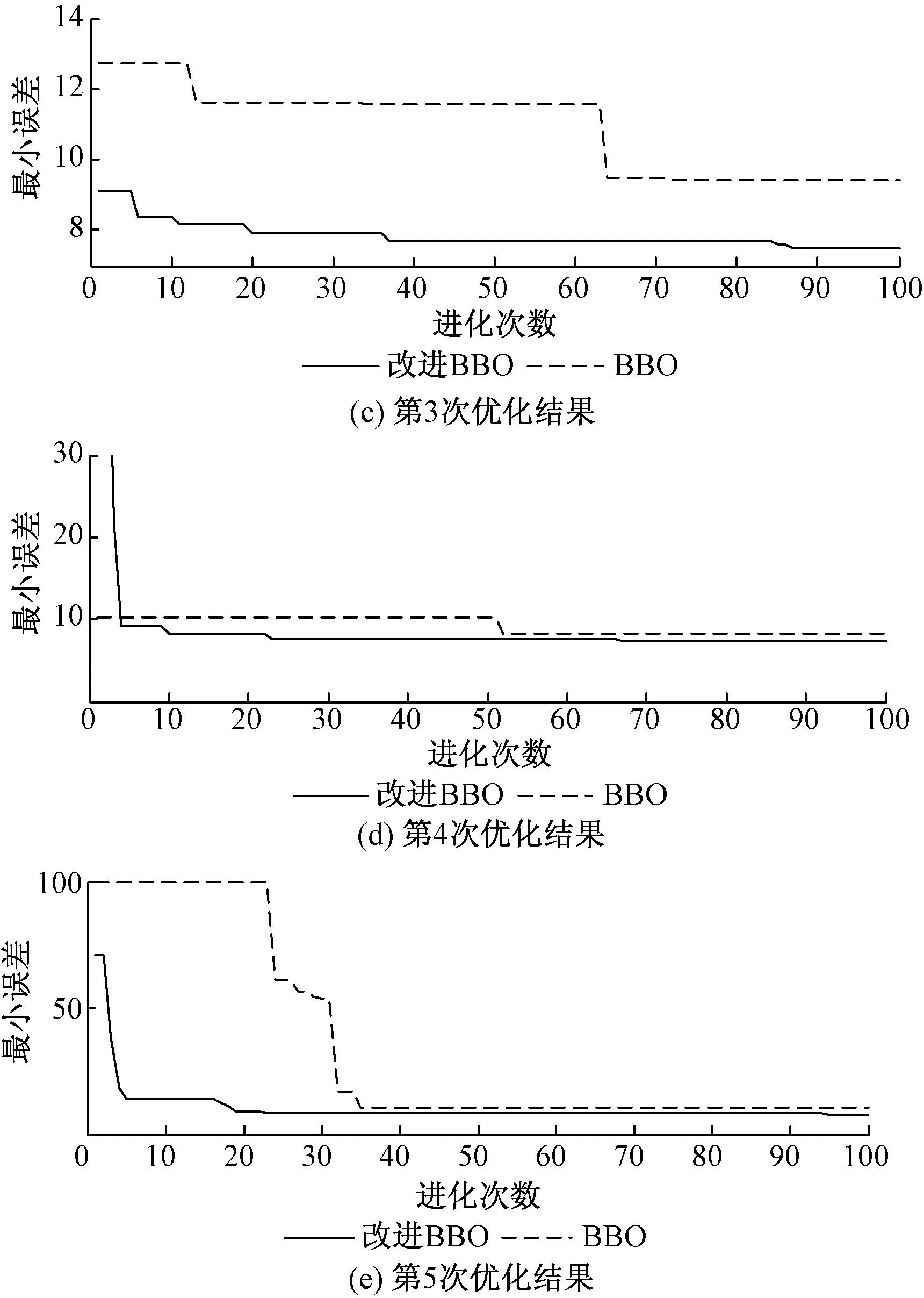
图3　连续5次优化最小误差曲线Fig.3　The minimum error curves of five optimizations

NumBBO改进BBO17.987.6428.157.7839.527.5148.347.32510.227.45

采用Matlab软件进行仿真试验,仿真时间ST=3 000 s。仿真结果如图4所示。

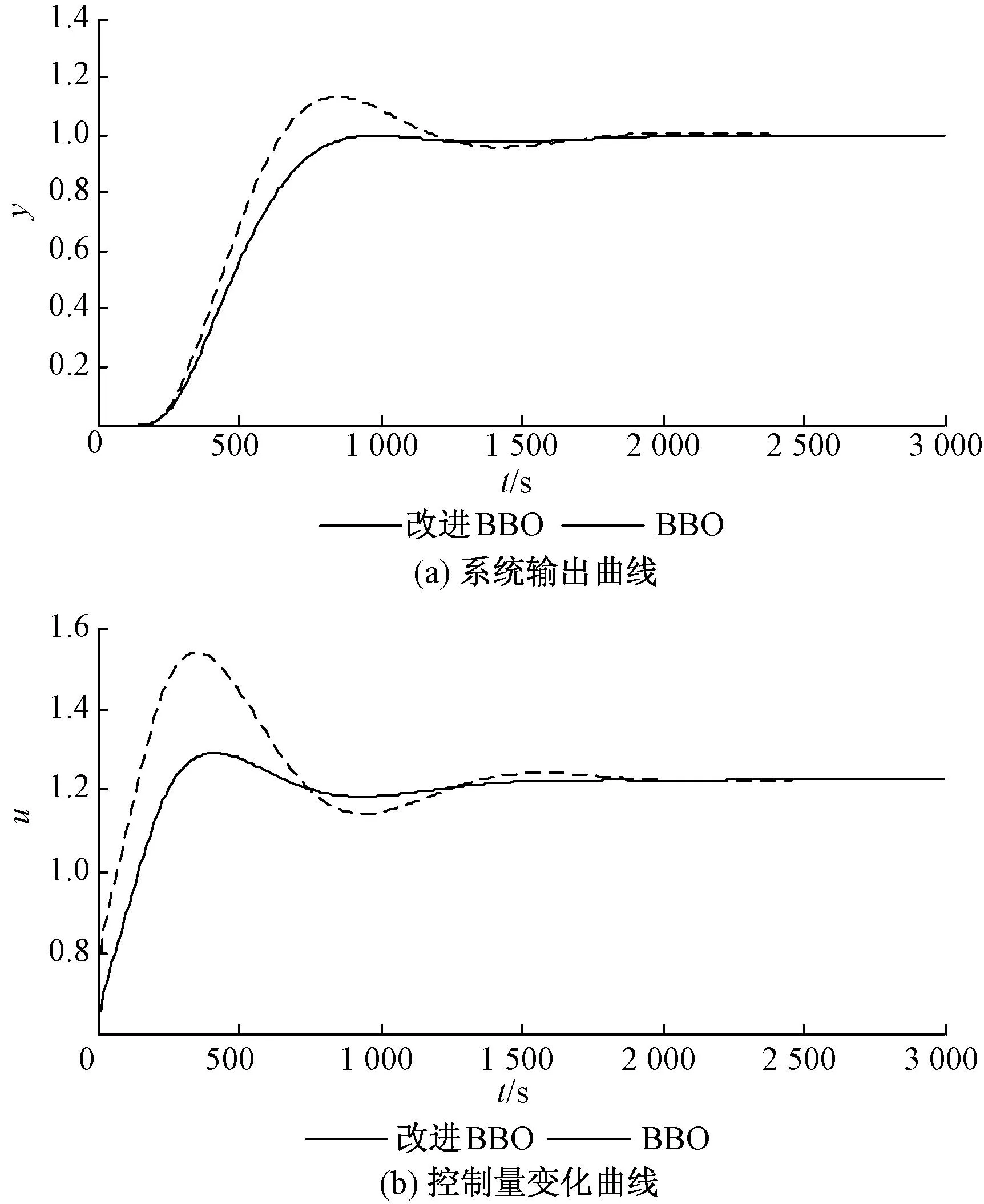
图4　系统阶跃响应曲线Fig.4　Curves of step response

图4可以看出，在改进BBO算法优化的PID控制器的控制作用下，系统超调量更小，并且快速稳定到了给定值，表现出良好的动态性能和稳态性能。另外从控制器输出来看，输出的幅值及震荡频率也更小，控制效果明显。

4结论

本文给出了一种改进的生物地理学优化算法，并将其成功的应用到PID控制器参数优化中。改进的算法在原有的迁移策略的基础上引入粒子群优化算法的寻优策略，使整个迁移过程具备一定的方向性，并采用淘汰策略剔除迁移突变后较差的参数。结果表明改进的BBO算法在热工系统PID控制器参数优化过程中收敛速度和收敛精度上较标准BBO算法有较大提高，且算法收敛结果更加稳定。

参考文献：

[1] 王存睿,王楠楠,段晓东,等. 生物地理学优化算法综述[J].计算机科学,2010,37(7):34-38.

[2] Bhattacharya A, Chattopadhyay P K. Hybrid differential evolution with biogeography-based optimization for solution of economic load dispatch[J].Power Systems,IEEE Transactions on, 2010, 25(4): 1955-1964.

[3] 李静文,赵晋泉,张勇.基于改进差分进化-生物地理学优化算法的最优潮流问题[J].电网技术, 2012, 36(9): 115-119.

[4] 郑肇葆.生物地理学优化(BBO)在图像分割中的应用[J].武汉大学学报(信息科学版), 2011, 36(8)：932-935.

[5] 毕晓君,王珏,李博. 基于生物地理学优化的雷达正交波形设计算法[J].吉林大学学报(工学版), 2014,(3):867-873.

[6] 刘伟,叶亚兰,司风琪,等.基于BP神经网络和SA-BBO算法的汽轮机组最优运行初压的确定[J].热能动力工程，2013，28(1):18-22.

[7] 马海平,李雪,林升东.生物地理学优化算法的迁移率模型分析[J].东南大学学报(自然科学版),2009,39(1)：16-21.

[8] 王芙丽,李平,曹江涛.改进的基于局部搜索策略的生物地理学优化算法[J].江南大学学报(自然科学版),2012,11(4):467-473.

[9] 雷敏,杨万里,彭晓波,等.基于改进简化粒子群算法的含DG的配电网无功优化[J].华北电力大学学报,2015,42(1):39-44.

[10] 崔晓波,陈雨亭,秦文炜,等.多模型块结构Laguerr函数预测控制在再热汽温系统中的应用[J].东南大学学报(自然科学版), 2013,43(4):803-808.

Improved BBO Algorithm and Its Application in PID Optimization of Thermal System

XUE Hong, HAN Pu

(Hebei Engineering Research Center of Simulation and Optimization Control for Power Generation, North China Electric Power University, Baoding 071003, China)

Abstract:In order to improve the performance of Biogeography Optimization (BBO) algorithm in PID controller parameter optimization of thermal systems and improve its optimization ability, this paper provides an improved BBO algorithm. The improved BBO algorithm introduces the searching strategy of Particle Swarm Optimization on the basis of original migration strategy, which leads the whole migration process to a certain direction. In addition, this algorithm employs phase-out strategy to remove poor parameters, obtained after the migration and mutation process. On one hand, the directional migration and elimination mechanism can ensure its fast convergence properties. On the other hand, mutational mechanisms can ensure the global characteristics of wide area searching, and avoid falling into local extreme value. Compared with the original BBO algorithm, the simulation results show that the improved BBO algorithm has better performance than the standard BBO algorithm on convergence speed and precision. It can be feasibly and effectively applied to PID controller parameters optimization in thermal system.

Key words：improved BBO algorithm; PID parameter optimization; simulation research

作者简介：薛虹(1990-)，女，硕士研究生，研究方向为智能优化算法及其在热工系统中的应用；韩璞(1959-)，男，教授，博士生导师，主要研究领域为大型火电机组建模及智能控制。

中图分类号：TP323

文献标识码：A

文章编号：1007-2691(2016)01-0081-05

基金项目：中央高校基本科研业务费专项资金资助项目(2014MS139).

收稿日期：2015-05-17.

doi:10.3969/j.ISSN.1007-2691.2016.01.14