基于新型两阶段混合算法的电力系统无功优化

黄　伟，田羽洲

(华北电力大学 电气与电子工程学院，北京 102206)



基于新型两阶段混合算法的电力系统无功优化

黄伟，田羽洲

(华北电力大学 电气与电子工程学院，北京 102206)

摘要：针对电力系统无功优化领域现有的人工智能算法易早熟和收敛精度不佳的缺点，将萤火虫算法和量子粒子群算法相结合，形成一种新型两阶段混合优化算法。该混合算法采用串联的方法将GSO算法与QPSO算法混合，使两种算法优势互补。在算法迭代前期充分利用萤火虫算法可同时搜索全部局部最优解的特性，保证了寻优的全面性。在迭代中后期，利用量子粒子群算法收敛速度快、解的精度高的特点进行寻优，保证了算法的收敛精度。同时基于黄金分割点理论，引入了群体替代算子，避免了迭代后期算法陷入局部最优。经过算法在IEEE30节点算例中的对比仿真，结果表明：在无功优化领域中，两阶段混合算法的全局搜索能力，收敛速度及精度均优于对比算法。

关键词：无功优化；电力系统；萤火虫算法；量子粒子群算法；群体替代算子

0引言

电力系统的无功优化是指在系统的初始状态已经满足所有约束条件且原始参数已知的情况下，以保证电能质量为前提，调节系统的可控变量(机端电压的调节、无功补偿设备的投切、变压器档位的变化)为手段，实现系统经济性运行为目的的多目标、多约束、非线性的电力规划问题[1]。

大量改进算法已经应用于无功优化领域，并在工程中解决实际问题。这些算法大致可以为分传统优化算法和人工智能算法[2]。传统算法如：线性规划法[3]和非线性规划法[4]。但此类方法对初值要求高，而且将离散参数进行了近似连续化处理，导致算法的优化效果不佳。人工智能优化算法如：遗传算法[5-6]、粒子群算法[7-8]、细菌算法[9-10]、萤火虫算法[11-12]。此类算法以随机搜索的方式对全局进行寻优计算，具有更加优秀的处理多目标、多变量、多约束的工程实际问题的能力，但也有着容易陷入局部最优、收敛速度慢、精度不高的缺点。文献[13]提出将遗传算法中的染色体组以小生境的形式分组，并利用群体共享机制提高算法搜索全局最优解的能力，但是过于依赖算法原始参数的设定。文献[14]中采用并行自适应粒子群算法。在粒子群寻优的过程中引入了利己、利他以及自主3个搜索方向，提升了粒子群算法的并行搜索能力。但是算法程序运行时间过长，效率不高。文献[15]在差分算法的基础上，引入了量子比特编码，增强了算法对解域空间搜索的全面性，但是算法的收敛速度较慢。文献[16]在粒子群算法中引入了量子理论，利用在束缚状态下的量子均会收敛于势阱中心的特点，优化了算法的收敛速度与精度，但算法在部分迭代过程中会出早熟现象，稳定性不高。文献[17]利用萤火虫算法解决了负荷优化问题。该算法参数少，易于实现，可以快速搜索解域内所有局部最优解，避免了算法的早熟，但该算法在迭代后期易出现峰值震荡现象，收敛精度不佳。

好的设计才会在当今社会有生存本能，在主要功能相近甚至相同的市场产品竞争的前提下，如何将产品竞争力扩大，考虑的不仅仅是形式上的提升，更有功能性的扩大，产品设计主要解决功能性，来源于原来的生活领域，来源于和环境的融合，不仅是外观和体量上与环境的融合，还包括功能与环境的融合，为的是让产品更能走入人们的生活中。好的设计的出现为的是让人们的生活更美好。

本文提出了将一种新型两阶段混合算法应用于电力系统无功优化中。该混合算法在迭代第一阶段利用萤火虫算子局部搜索能力强的特点，快速优化搜索种群，并在迭代第二阶段引入了量子粒子群算子保证了迭代的速度与精度。同时，根据黄金分割点的在自然界中的意义，在算法中引入了群体替代算子，进而使主搜索群的优势粒子不断更新，避免了迭代后期因主搜索群个体的单一化而导致算法早熟的现象，保证了种群的多样性。最后，将本文提出两阶段混合算法与两种对比算法在IEEE30节点的算例中进行仿真比较。

1无功优化的数学模型

本文以系统有功损耗最小为目标建立无功优化数学模型，表达式如下：

(1)

式中：PLoss为系统有功损耗；Gij为导纳矩阵的实部；Ui、Uj为节点i、j的电压。θij为节点i与j的相位差；H为网络支路数。

电力系统无功优化模型中，其等式约束为模型参数需要满足系统潮流方程的要求，即：

(2)

主搜索群粒子位置根据下式更新：

模型中的不等式约束分为状态变量约束和控制变量约束两部分。其中，状态变量约束主要以系统中的发电机节点和负荷节点为研究对象，具体约束如式(3)；而控制变量约束主要以系统中的3类可控变量为研究对象，具体约束如式(4)。

模型的状态变量约束为

(3)

本案例从变量分析入手引导学生进行层层实验探究，领悟实验设计的过程和方法；以问题串方式引导学生层层深入分析思考，掌握实验设计原则和方法，学会确定变量、控制变量，从而有效提高学生的生物实验设计能力，培养其自主探究能力，提高生物学学科核心素养。

因此，本文通过总结目前医养结合养老服务评价研究的现状，依据系统理论和相关利益者理论，结合采用DEA评价方法，对医养结合服务进行绩效评价模型的设计，并以青岛市养老服务机构为例进行实证分析，提出改进医养结合养老服务的路径，以弥补现有研究的不足，促进医养结合养老服务的新发展。

模型的控制变量约束为

(4)

式中：NG表示系统中发电机节点总数；UGimin，UGimax分别为发电机端电压阈值；NT表示系统中支路中所含变压器总数；Timin，Timax分别为可调变压器分接头位置的阈值；NC表示系统中装设有无功补偿装置的节点总数；QCimin，QCimax为容性无功补偿量的阈值。

我们对大数据方法的认识却还需要做深入思考，我们需要辨析网络世界舆情与现实世界舆情的关系，需要思考采用大数据方法抓取到的网络数据对全体公民意见的代表程度。

(5)

(6)

(7)

式中：u为在[0,1]区间内服从均匀分布的随机数L由下式确定：

2两阶段混合算法的原理及应用

2.1GSO算法的原理

GSO算法是基于萤火虫求偶行为中荧光素越高，吸引力越强的生物学原理，通过建立萤火虫个体荧光素值与数学模型中目标函数的联系，在求解空间内寻优。该算法首先在一个D维求解空间中随机生成K个随机萤火虫个体(每个萤火虫个体代表求解空间的一个解)，每一个萤火虫个体都带有一定量的荧光素值：li(i=1,2,3,…,K)。设定萤火虫个体的感应半径为rdi，只有在感应半径之内，萤火虫个体才会寻找到荧光素更高的个体。为保证算法与模型目标函数寻优方向的一致性，萤火虫个体会根据如下方程更新荧光素值：

(8)

式中：li(t)表示在第t次迭代时荧光素值的大小；ρ 表示荧光素值挥发系数；γ表示荧光素值增强系数；minF(xi(t+1))表示萤火虫个体i在第t+1次迭代时对应网损的大小。

由于在个体i的感知范围内可能存在多个荧光素值大于其本身的优势个体，为保证算法的全面性，将位于个体i的感知范围内的优势个体利用集合的形式表示，如式(9)：

(9)

式中：dij表示个体i与其感知范围内优势个体j之间的距离。

根据集合It中优势个体的荧光素值，选出目标个体，并使个体i向着目标个体的方向进化。式(10)为优势个体被选为目标个体的概率公式。

在电力系统实际运行过程中，可以将上述状态变量的越限情况以罚函数的形式加入到无功优化模型的目标函数中：

(10)

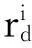
(11)

式中：s表示移动步长；Xi(t)表示个体i移动前的位置；et表示个体i移动后的位置。

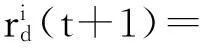
(12)

式中：rs为个体i的感知范围；β为感知半径收缩系数；et为个体i感知范围内优势个体的数量。

综上所述，胸痛护士主导的标准化工作流程简单明了，程序化、规范化、科学化的操作既方便临床护理实践，缩短了胸痛患者在急诊的停留时间，提高抢救成功率，提高医护和患者满意度，提升社会经济效益，又方便于各层级医院的临床学习和教学，具有较高的社会价值，值得推广应用。

领域子系统是对真实物理世界的数据抽象，包括几何模型，网格模型，边界条件和载荷，材料，特征属性以及结果。

2.2QPSO算法的原理

通过调研现有的粉体物料皮带输送机清扫技术，开展集成清扫技术在硫磺皮带输送机上的应用研究，研制出一种集“皮带复合清扫、粉尘密闭收纳、自动回收”于一体的多功能集成清扫装置，将皮带面上黏附的物料清除，并通过物料回收机构降低转运现场落地硫磺量，减少硫磺粉尘污染，实现硫磺输送系统安全平稳运行。样机安装区域硫磺粉尘质量浓度小于10 g/m3的技术指标[4-5]，符合粉尘防爆、安全规范要求。

QPSO算法是针对PSO算法粒子以轨道的形式进行寻优，寻优区域不能覆盖整个解域的缺点，结合量子物理中粒子具有波粒二象性的思想改进而成。在应用GSO算子进化出新的种群后，种群最优位置为Pi(t)=[Pi1(t),Pi2(t),…,PiD(t)]，全局最优位置为Gi(t)=[Gi1(t),Gi2(t),…,GiD(t)]，其中，G(t)=Pg(t)，g为处于全局最好位置粒子的下标，g∈{1,2,…,K}。然后通过粒子的波动性函数描述粒子的状态，并根据薛定谔方程求出粒子出现在空间某一点的概率密度函数，最后粒子的位置由蒙特卡洛随机模拟得出。

(13)

式中：λV、λQ分别为电压幅值越限和发电机无功出力越限惩罚系数；FV为状态变量节点电压的越限罚函数；FG为发电机输出的无功功率越限罚函数；ΔUi和ΔQGi分别为节点电压和发电机无功出力的越限偏差。

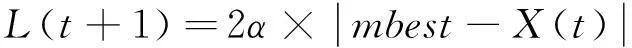
(14)

最后，量子粒子群的进化方程为

(15)

(16)

(18)

即：α随着迭代线性地从m递减到n，通常m=1，n=0.5，MaxTimes是算法迭代的最大次数。当α≤0.5时，式(17)取“—”，当α>0.5时，取“+”。

(亚伦)“在金牛犊脚下筑起一座祭坛，高声宣布：明天，是耶和华的节日！次日一早，众人献上全燔祭和平安祭。礼成，坐下一起吃喝，营地一片欢乐。

2.3群体替代算子的引入

2.4基于两阶段混合算法的无功优化流程

式中：N为系统中的节点总数；PGi为发电机节点i发出的有功功率；PLi为节点i的有功负荷；QGi为发电机节点i发出的无功功率；QCi为节点i上无功补偿装置的无功补偿量；QLi为节点i的无功负荷。

(19)

辅搜索群粒子位置根据下式更新：

(20)

式中：φ1、φ1、φ1均为在[0,1]区间上的随机数。其余表达式的含义与前面QPSO算法中所述相同。

由于黄金分割比例体现了自然界中事物的美感与和谐，而量子粒子群算法本质是采用了仿生学的原理，所以每次替换粒子的比例采取0.618的黄金分割比例。即将辅搜索群适应值较好的前(1-0.618)K=0.382K个个体与主搜索群中适应值较差的后0.382K个个体进行交换，进而实现了搜索群的更新。

式中：NG为系统中发电机节点数；Uimin，Uimax为系统节点i的电压阈值；NL为系统中负荷节点数；QGimin，QGimax分别为发电机无功出力阈值。

过引入群体替代算子改进量子粒子群算法，避免了算法因搜索种群多样性匮乏而陷入局部最优。群体替代算子以形成主搜索群与辅搜索群的方式体现在算法中，其中主搜索群采用全局搜索的方式，辅搜索群采取局部搜索的方式。在每次迭代时，在辅搜索群中选取一定比例优势粒子替代主搜索群中劣势粒子。这样既保持了在迭代过程中主搜索群的速度，同时由于有新的粒子不断地补充，也保证了群体的多样性。

将本文所提出的两阶段混合算法与电力系统无功优化的工程实际相结合，步骤如下：

(1)输入两阶段混合算法所需参数以及系统初始运行参数，其中包含发电机、负荷节点、输电线路以及可调变压器初始参数。

(2)根据系统中三类控制变量的范围初始化主搜索群与辅搜索群的粒子。

2.2 两组患者的血清钙、磷水平比较 治疗前，两组患者的血钙、血磷水平比较，差异无统计学意义(P>0.05)，治疗后均有所改善，研究组显著优于手术组，差异有统计学意义(P<0.05)。见表2。

(3)置GSO算子迭代次数tG=1，进行潮流计算并根据式(8)更新两个搜索群的荧光素值。

(4)根据式(9)、(10)、(11)更新两个搜索群中每个粒子的位置，并根据式(12)更新粒子的感知半径。

(5)置tG=tG+1，并判断是否达到GSO算子部分的迭代最大次数，如果达到进行下一步寻优，否则转至步骤(4)。

(6)置QPSO算子迭代次数tQ=1，计算此时主、辅搜索群中每一条粒子对应的系统潮流，根据式(5)计算出适应度函数， 并记录首次迭代的最佳位置和相应适应度值。

我国能源发展面临着三大核心问题。一是安全发展问题。随着能源需求不断增加，除了要增强国内供应保障外，增加海外能源资源供应成了必然选择。如何保障能源进口安全是长期挑战。二是清洁发展问题。长期以来，我国高度依赖煤炭的粗放低效发展方式，不仅导致资源大量浪费，而且造成了严重环境污染。如何实现能源清洁发展是当前及今后一段时期生态文明建设的瓶颈。三是低碳发展问题。2014年全球二氧化碳排放量为355亿吨，其中我国高达97.6亿吨，占全球的四分之一以上，燃煤贡献了主要的二氧化碳排放量。解决这三大问题，需要国家在推动能源革命过程中，针对问题紧迫程度，采取相应策略性手段和措施。

(7)根据式(15)分别计算两个搜索群mbest值。

随着临床医疗管理模式的改变，围术期医学的发展成为必然，作为“幕后英雄”的麻醉医生即将走向“台前”，向围手术期医生转变，因此人文关怀精神将成为麻醉医生的必备素养。让患者在心理和生理上都减少乃至无痛苦，是我们需要努力达到的目标。

(8)主搜索群根据式(19)，辅搜索群根据式(20)分别向各自搜索群中的最优位置进化。

(9)更新并排序两个搜索群的各粒子的适应度值。

(10)根据黄金分割点理论，辅搜索群的前0.382N个优势个体替换主搜索群的后0.382N个劣势个体，计算更新后的主搜索群粒子的适应度值，并更新全局最优解以及全局最优粒子。

(11)置tQ=tQ+1，并判断是否达到QPSO算子部分的最大迭代次数要求，如果没有达到要求，则返回步骤(7)；如果达到要求，则输出结果。算法的流程如图1所示。

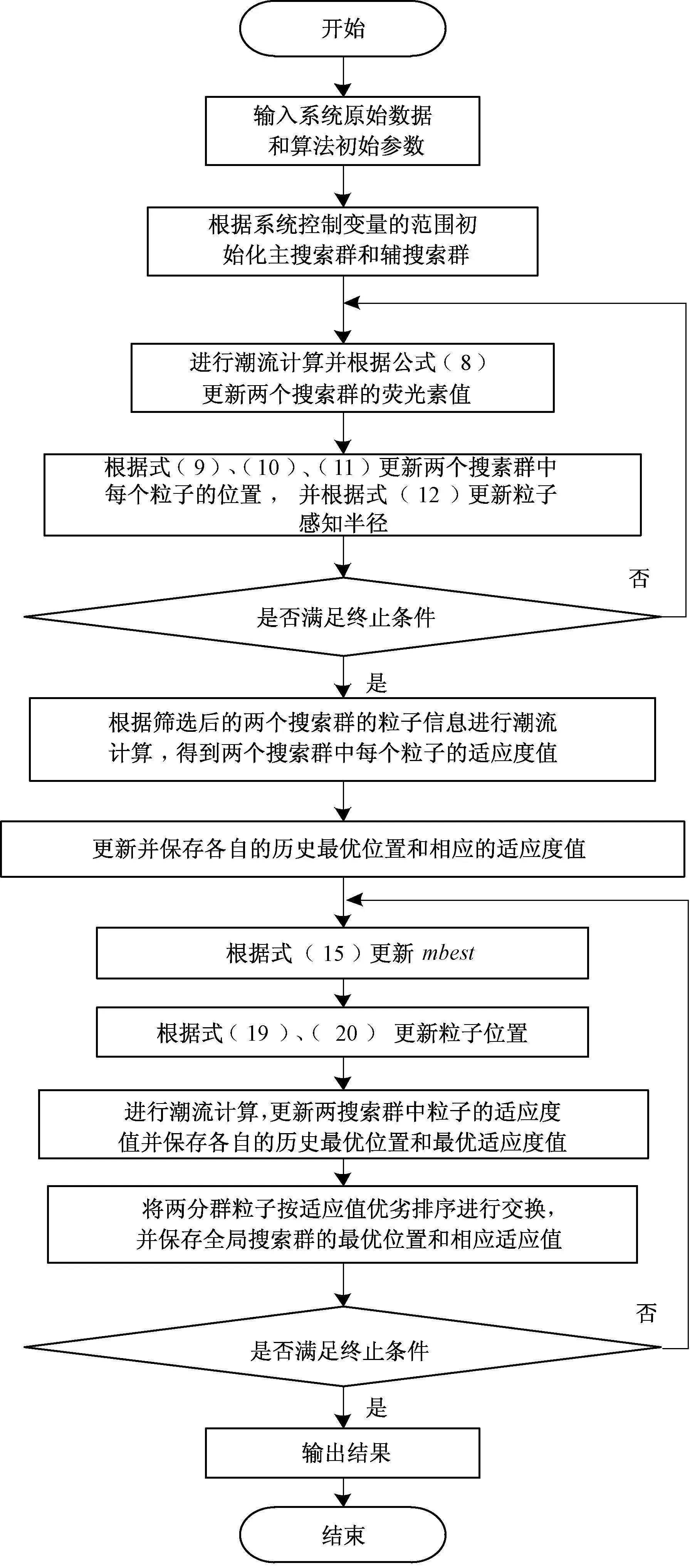
图1　基于两阶段混合算法的无功优化流程图Fig.1　Flow chart of reactive power optimization with the two-stage hybrid algorithm

3算例分析

本文通过IEEE30节点测试系统验证混合算法的有效性。该系统的6台发电机位于节点1、2、5、8、11、13。其中，1为平衡节点，2、5、8、11、13为PV节点[18]。发电机机端电压范围是[0.9,1.1]；系统有22个PQ节点，其中10节点和24节点是无功补偿点，步长为0.1；41条支路，其中，支路6-9、6-10、4-12和27-28为变压器支路，步长为0.025。算法参数和控制变量范围如表1～4。

表1　两阶段混合算法的参数

表2感知半径、感知范围和收缩系数对应值

Tab.2Corresponding values of the perception radius、perception ranges and contraction coefficients

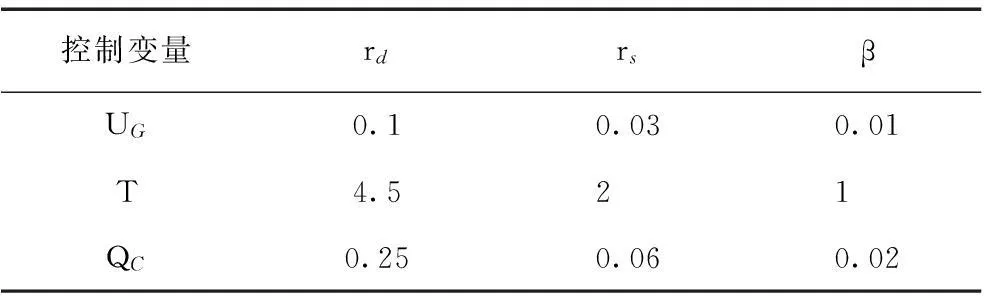
控制变量rdrsβUG0.10.030.01T4.521QC0.250.060.02

表3　发电机无功出力上下限值

表4　控制变量的上下限值

根据系统的初始状态，通过潮流计算，初始潮流的有功损耗Ploss=7.69 MW。

为了验证本文所提出的两阶段混合算法的有效性，分别与基本QPSO算法和GSO算法作对比，其中两种对比算法迭代次数设置为100。3种算法连续运行50次，比较各种算法的最优、最劣和平均网损值，统计结果见表5。

手术费用目前仍是影响患者及家属决定手术方式的因素之一。本研究3节段组的手术费用明显低于5节段组（P＜0.05）。微型钛板使用数量的下降减少了手术费用，手术费用昂贵目前仍是微型钛板在临床推广应用的阻碍。对于需要行颈椎后路椎管扩大椎板成形术的患者，使用微型钛板固定的疗效虽然明显优于传统丝线缝合固定［14］，但其费用也远高于丝线缝合固定。因此减少微型钛板使用数量，可缩小两者之间的费用差距，更好的扩大微型钛板在颈后路椎管扩大椎板成形的应用。

空间调制系统的ML检测算法中，hlx需要4Nr次实数乘法，计算矢量的范数需要2Nr次实数乘法，由于ML检测要搜索所有的天线和符号，因此ML检测的计算复杂度为CML= 6MNtNr[13].

表53类算法优化效果对比

Tab.5Contrast of optimization effects by three relevant algorithms

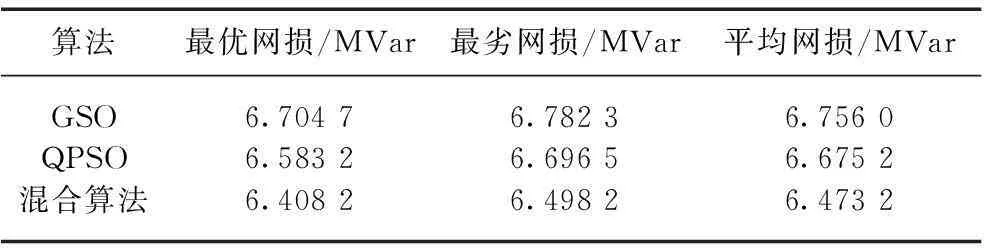
算法最优网损/MVar最劣网损/MVar平均网损/MVarGSOQPSO混合算法6.70476.58326.40826.78236.69656.49826.75606.67526.4732

由表5结果可知，在分别进行50次优化后，在减小网损这一优化指标中，本文所提出的两阶段混合算法优于单一的GSO与QPSO算法。其中以平均网损为例，本文所提算法比GSO和QPSO算法分别降低4.1%和3.0%，说明该混合算法可有效搜索全局最优解，降低系统网损。

图2为三类算法的网损收敛曲线。从曲线的收敛速度与精度可以看出：GSO算法有较快的收敛速度，在20代左右就已经收敛，但是算法的寻优效果不佳，易陷入局部最优解。QPSO算法寻优效果较好，但是收敛速度较慢。而混合算法结合了二者的优点，不仅收敛速度快，而且收敛精度高，可以很好的降低系统的网损。因此，对于电力系统的无功优化，该算法是一种理想可行的算法。

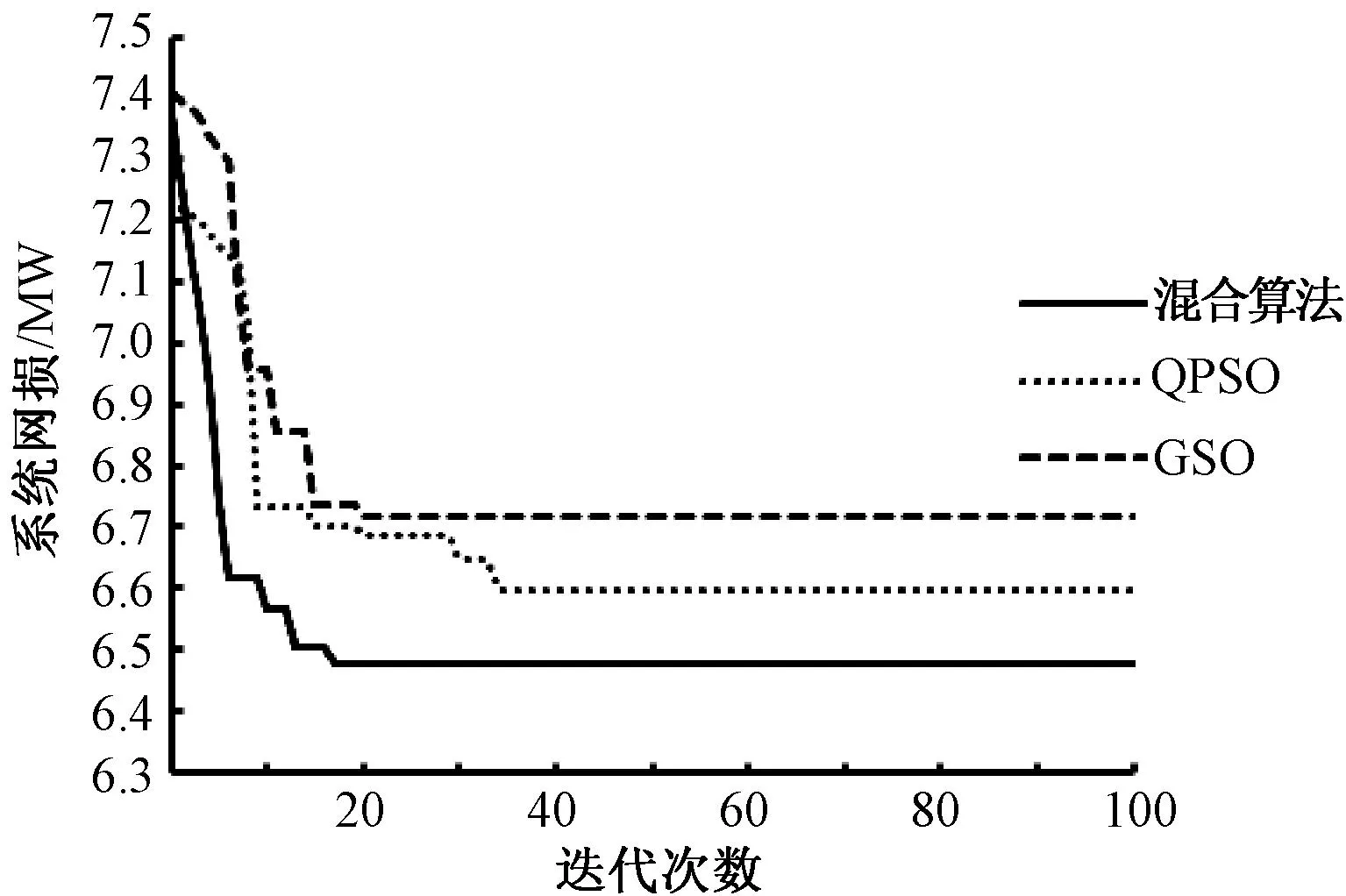
图2　混合算法、QSO和GSO算法的网损收敛特性曲线 Fig.2　Convergence curve of hybrid、QSO and GSO algorithms

图3为经过混合算法、QPSO算法与GSO算法的优化后，IEEE30节点系统的节点电压幅值波动曲线，由图3知，无功优化后的系统电压均可以保证在[0.95,1.05]的范围内，但是系统应用混合算法无功优化后的电压曲线比应用GSO和QPSO算法后的电压曲线更为平稳，因此，通过应用混合算法，系统能保持良好的电压水平。

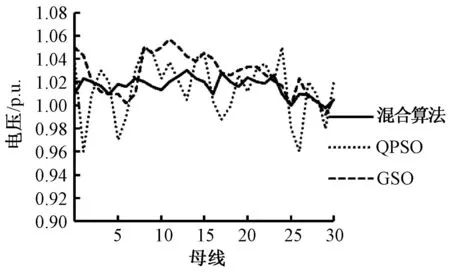
图3　IEEE 30 节点系统电压幅值Fig.3　IEEE 30 bus system voltage magnitude

4结论

提出的两阶段混合算法在迭代前期经过GSO算子的局部筛选，过滤出性能更优的粒子，保证了寻优的全面性。在算法的中后期，经过QPSO算子的迭代，保证了算法的收敛精度和速度。同时引入群体替代算子，避免了搜索群在迭代后期因缺乏多样性而陷入局部最优。通过算例仿真结果可知，混合算法可以在较少的迭代次数里，更快更准确地收敛到全局最优解，同时可以保证电力系统节点电压的稳定性。本文所提出的两阶段混合算法可以有效地应用于电力系统无功优化领域。

参考文献：

[1] 张勇军，任震，李邦峰．电力系统无功优化调度研究综述[J] ．电网技术，2005，29(2)：50-56．

[2] 刘华臣,王锡淮,肖健梅,等. 基于群搜索算法的电力系统无功优化[J].电力系统保护与控制, 2014(14):93-99.

[3] Baran M E，Wu F F.Optimal capacitor placement on radial distribution systems[J].Power Delivery, IEEE Transactions on， 1989,4(1)：725 - 734．

[4] Momoh J A，Adapa R ,El-Hawary M E．A review of selected optimal power flow literature to 1993. I. Nonlinear and quadratic programming approaches [J] ．IEEE Transactions on Power Systems，1999，14(1)：96-104．

[5] 张粒子，舒隽，林宪枢，等．基于遗传算法的无功规划优化[J]．中国电机工程学报，2000，20(6)：5-8．

[6] 蒋平,梁乐. 基于内点法和遗传算法相结合的交直流系统无功优化[J]. 高电压技术,2015,41(3):724-729．

[7] 张文，刘玉田．自适应粒子群算法及其在电力系统无功优化中的应用[J]．电网技术，2006，30(8)：19-24．

[8] 雷敏,杨万里,彭晓波,等. 基于改进简化粒子群算法的含DG的配电网无功优化[J]. 华北电力大学学报,2015,42(1):39-44.

[9] 张晓辉,卢志刚,秦四娟. 基于改进细菌群体趋药性算法的电力系统无功优化[J]. 电网技术,2012,36(2):109-114.

[10] 陈继明,王元元,高艳亮. 基于改进细菌群体趋药性算法的配电网无功优化[J]. 电力系统保护与控制,2012，40(14):97-102.

[11] Du M, Lei X, Wu Z. A simplified glowworm swarm optimization algorithm[C]//Evolutionary Computation (CEC), 2014 IEEE Congress on. IEEE, 2014: 2861-2868.

[12] Lu X, Sun W. An improved self-adapting Glowworm Swarm Optimization algorithm[C]//Signal Processing, Communication and Computing (ICSPCC), 2013 IEEE International Conference on. IEEE, 2013: 1-4.

[13] 崔挺,孙元章,徐箭, 等. 基于改进小生境遗传算法的电力系统无功优化[J]. 中国电机工程学报,2011，31(19):43-50.

[14] 刘世成,张建华,刘宗岐. 并行自适应粒子群算法在电力系统无功优化中的应用[J]. 电网技术,2012,36(1):108-112.

[15] 马玲,于青,刘刚,等. 基于量子差分进化算法的电力系统无功优化[J]. 电力系统保护与控制,2013，41(17):39-43.

[16] 王智冬,刘连光,刘自发,等. 基于量子粒子群算法的风火打捆容量及直流落点优化配置[J]. 中国电机工程学报,2014，34(13):2055-2062.

[17] 王晶,王宗礼,陈骏宇,等. 基于萤火虫优化算法的微网源—荷博弈模型及分析[J]. 电力系统自动化,2014，38(21):7-12.

[18] 张金环,安海霞,王永春. 基于改进小生境帝国竞争算法的多目标电力系统无功优化[J]. 华北电力大学学报,2014,41(4):41-47.

Var Optimization of Power System Based on Novel Two-stage Hybrid Algorithm

HUANG Wei, TIAN Yuzhou

(School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206, China)

Abstract:In allusion to the defects of artificial intelligent algorithm in var optimization, such as the prematurity and slow convergence speed, Glowworm Swarm Optimization (GSO) and Quantum-behaved Particle Swarm Optimization (QPSO) are combined to form a novel two-stage hybrid algorithm. In order to remain the advantages of the two kinds of algorithms and weaken their defects, the strategy of connecting GSO and QPSO in series is put forward in the hybrid algorithm. GSO is fully used in the former steps to search for all the global optimal solutions, thus the comprehensiveness of the optimization is ensured. Due to the advantages of the fast speed and high accuracy of the convergence, QPSO is applied in the Middle-Later Period of the iteration to ensure the convergence precision of the algorithm. During the search process of the QPSO, population substitution operator based on the golden point theory is applied to prevent the low efficiency and local optimum of the algorithm. Comparative simulation results of IEEE 30-bus system show that as for var optimization, the global searching ability，convergence speed and accuracy of the two-stage hybrid algorithm are superior to the contrast algorithms.

Key words：var optimization; power system; glowworm swarm optimization; quantum-behaved particle swarm optimization; population substitution operator

作者简介：黄伟(1962-)，男，教授，研究方向为智能电网和新能源利用技术，微电网技术，电力系统分析、运行与控制等；田羽洲(1990-)，男，硕士研究生，研究方向为电力系统运行与分析、微电网技术等。

中图分类号：TM712

文献标识码：A

文章编号：1007-2691(2016)01-0046-06

收稿日期：2015-06-20.

doi:10.3969/j.ISSN.1007-2691.2016.01.08