一种降维求解机组组合问题的双重粒子群优化算法

翟俊义，任建文，李　整，周　明

(华北电力大学 新能源电力系统国家重点实验室，河北 保定 071003)



一种降维求解机组组合问题的双重粒子群优化算法

翟俊义，任建文，李整，周明

(华北电力大学 新能源电力系统国家重点实验室，河北 保定 071003)

摘要：考虑机组组合的电力系统动态经济调度是一个高维复杂的非线性优化问题。提出了一种采用降维思想解决大规模机组组合问题的新方法，降维的方式是将对整个调度周期的优化转化为对每个调度时刻依次、分别优化，即将对矩阵的优化转化为对行向量的优化，降低求解维数。结合离散与连续粒子群(particle swarm optimization，PSO)算法，分别得到当前调度时刻最优的机组组合状态及对应的最优负荷分配。采用初始化策略提高初始解质量，并对机组启停、爬坡等约束条件处理，使寻优都在可行域中进行，结合优先次序法及智能调整策略避免算法早熟。算例表明本文方法在经济性上具有很大的优越性，且可明显减少开机机组数目，对于求解机组数较多的大规模系统更具优势。

关键词：机组组合；降维优化；动态经济调度；大规模系统；双重粒子群算法

0引言

电力系统机组组合UC(Unit Commitment)问题是一个高维的离散混合非线性优化问题。解决UC问题的方法有经典算法和新型智能算法，经典算法主要有优先次序法(PL)[1]、动态规划法(DP)[2]、拉格朗日松弛法(LR)[3]等。PL法按机组单位耗量排序，该算法一般忽略机组启停费用，计算量小，但不能保证获得最优解；DP法存在“维数灾”问题；LR法存在收敛稳定性和对偶间隙问题。经典算法对小规模系统具有求解快速的优点，然而随着系统规模的扩大及约束条件的增多，传统的经典算法难以获得精确的最优解。

近年来，相关学者对UC问题进行了大量研究，但是解决UC问题的方法都很类似，几乎都是在暂不考虑启停时间约束的条件下，同时优化所有调度时刻的机组组合状态，再进行局部调整，以满足全部约束，其调整存在盲目性且寻优效率不高，随着系统规模的扩大及参与调度的机组数增加，传统处理方法的寻优时间复杂度增加且难以获得令人满意的调度策略。文献[4]采用改进蚁群算法求解UC问题，但对蚁群算法的改进并不大，没有体现算法出在机组数较多时候的适用性。文献[5]同时考虑环境和经济最优，用线性加权处理多目标问题，采用一种混沌遗传混合算法求解UC问题，且考虑了网损及汽轮机的阀点效应，但优化结果中并未体现机组爬坡约束的限制。文献[6-11]都将UC问题分解为内外两层优化，外层优化机组启停，先不考虑启停时间约束，对所有调度时刻同时进行机组组合状态优化，再进行局部调整，以保证同时满足启停时间约束与功率平衡约束；内层是根据外层确定的全调度周期内最优的机组组合状态，优化机组负荷分配。文献[12]先确定第一个时刻最优的机组组合状态，再确定第二个时刻，依次类推，得到全调度周期内最优的机组组合状态。在已知全调度周期内最优机组组合状态的条件下，再优化机组负荷分配。文献[12]的方法具有一定的新颖性，但仍需首先优化出全调度周期内最优的机组组合状态后，再优化该最优机组组合状态对应的机组出力，增加了算法时间复杂度。

本文提出一种全新的采用降维思想处理UC问题的方法，降维的方式是将对整个调度周期的优化转化为对每个调度时刻依次、分别优化，并计及启停时间的向后约束和向前继承，将对矩阵的优化转化为对行向量的优化，降低求解维数。结合离散与连续粒子群算法，分别得到当前调度时刻最优的机组组合状态及对应的最优负荷分配，并对初始解质量、约束处理、算法早熟等问题提出改进策略。仿真结果表明，本文方法在调度经济性方面具有很大的优越性，且可明显减少开机机组数目，对于机组数较多的大规模系统更具优势。模型经适当修改，可应用到含大量分布式电源的微网调度模型中，具有广泛的适用性。

1考虑机组组合的动态经济调度模型

1.1目标函数

火电机组运行费用目标函数。包括发电费用和机组启动费用，并考虑汽轮机的阀点效应。

(1)

(2)

(3)

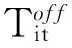
1.2约束条件

1.2.1基本约束条件

(1)系统功率平衡约束，暂忽略网损。

(4)

(2)发电机输出功率上下限约束。

(5)

(3)机组旋转备用容量约束。

(6)

(4)机组爬坡、滑坡速率约束。

(7)

(8)

(5)机组最小启停时间约束。

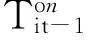
1.2.2机组出力上下限及爬坡速率约束的处理

(2)对于t>1时刻，t-1时刻的机组最优出力安排会影响当前时刻的机组出力。对于机组i而言：

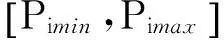
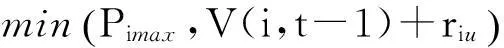
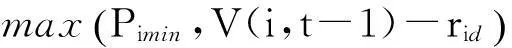
其中：V(i,t-1)为t-1时刻机组i的最优出力值。

1.2.3开机机组数约束

(11)

本约束是为解决因启动机组数过多，而导致连续PSO算法优化出力分配时不满足机组出力上下限约束的问题。式中β∈(0,1)，以避免出现少数机组出力值稍大于出力下限，导致其他机组找不到满足上下限的出力值的问题，取β=0.8。

2粒子群算法概述

2.1离散粒子群算法

在机组组合问题中，离散PSO算法的速度和位置更新公式为

(12)

(13)

结合机组的最小启停时间约束，式(13)变为

(14)

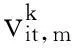
2.2连续粒子群算法

在机组组合问题中，连续PSO算法的速度和位置更新公式为

(15)

(16)

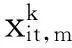
连续PSO与离散PSO算法均采用动态惯性权重系数：

(17)

式中：ωinitial、ωfinal为惯性权重系数的初始值和终值；g_max表示最大迭代次数；k表示当前代数。

3粒子群算法在降维求解机组组合问题中的应用

3.1降维思想的应用

传统优化方法大多是在暂不考虑启停时间约束的前提下，对所有调度时刻同时进行随机优化，然后采用盲目性较大的局部替换调整方法，以保证满足单机约束和系统约束。这样不能保证初始解一定位于可行域内，对机组数较多的大规模系统，很难快速找到最优的机组组合状态。

本文降维优化的思想是将对整个调度周期的优化转化为对每个调度时刻依次、分别优化，即将对矩阵的优化转化为对行向量的优化，降低求解维数。对于当前正在优化的调度时刻，所有开机机组都必须严格满足最小启停时间约束和功率平衡约束，计及启停时间的向后约束和向前继承，即前面调度时刻机组的启停安排会影响当前时刻的机组启停。

3.1.1机组启停状态的初始化

(1)确定机组的开机优先权λi。参照优先次序法[13]思想，根据机组满负荷运行时平均单位耗量的高低，确定机组i的开机优先权λi，平均单位耗量越低的机组，其开机优先权λi越大，且λi∈[0,1]，即机组i的开机概率。

(2)确定基荷机组。根据已确定好的机组开机优先权，挑选开机优先权较高的前20%的机组作为基荷机组持续运行。

对当前调度时刻某机组启停状态的初始化，需考虑启停时间的向前继承。首先判断前一个时刻该机组是否已满足最小启停时间约束，若满足，则按机组开机概率初始化；若不满足，则继续保持上一个时刻的运行状态。对于第一个调度时刻机组启停状态的初始化，需计及前一天机组已经连续开机或停机的时间。

3.1.2迭代更新策略

由于将对整个调度周期的优化转化为了对每个调度时刻依次、分别优化，因此每个调度时刻的优化过程类似。

每个调度时刻，在初始化完机组组合状态后，参照已确定的前些调度时刻的最优机组组合状态，判断机组是否已满足最小启停时间约束，若满足，则按式(14)更新机组启停状态，否则，保持上个时刻的运行状态。对更新过程中机组组合的每个中间结果用连续PSO算法优化出力分配，以判别是否为当前调度时刻的最优机组组合状态，最终得到当前调度时刻的最优机组组合状态及对应的最优负荷分配。

已优化完成的时刻，将最优的机组组合结果存放在矩阵U中，对应的最优机组出力值存放在矩阵V中。若要优化下一个时刻，只需参照U中存放的前些调度时刻的最优机组组合状态，判断是否已满足最小启停时间约束即可。在优化完所有调度时刻后，即得到全调度周期内最优的机组组合状态矩阵U及对应的最优负荷分配矩阵V。同样，对于第一个调度时刻的迭代优化，需计及前一天机组已经连续开机或停机的时间。

迭代时，可能存在某个调度时刻，即便将所有满足最小停机时间约束的机组都开机且满发，也不能满足功率平衡与备用约束，导致当前调度时刻优化失败。原因是式(14)更新具有随机性，使某些机组在前面某时刻已经停机，而在当前时刻，这些机组还不满足最小停机时间约束，不能开机，导致当前时刻可开机的机组数较少。因此，还需考虑启停时间的向后约束，即对于当前调度时刻t，在确定完本时刻的机组组合状态之后，还需进行如下操作：

在本时刻下所有不满足最小停机时间约束的停机机组集中，找出还需保持停机状态的最大时段数，假设为t0小时，则从当前t时刻往后顺推t0小时，判断这t0个小时是否都满足功率平衡与备用约束，若不满足，则需重新优化当前时刻t的所有机组组合状态，直到满足为止。

3.2智能调整策略

对于每个调度时刻，在算法迭代后期，最优的机组组合状态可能不发生改变，算法早熟可能陷入局部最优，并且可能出现某时刻开机数较多，系统备用过剩的情况，因此本文采取了智能调整策略。

3.2.1开机机组数的调整

对每个调度时刻，记录最优机组组合状态保持不变的持续代数，并设置持续代数上限值。当持续代数达到上限时，将已满足最小开机时间约束的机组中开机优先权较小的一台机组置停机，若仍满足功率平衡与备用约束，则调整结束；若不满足，则再将已满足最小停机时间约束的机组中开机优先权较大的一台机组置开机，再判断是否满足约束，以减少开机机组数，并实现多开较优机组，少开较劣机组的目的。持续代数上限值可根据实际情况设置，本文认为若最优机组组合状态保持不变的持续代数达到了最大迭代次数的一半左右，即达到了持续代数的上限值，需要进行智能调整。

3.2.2旋转备用约束满足的调整

在每次迭代更新时，仅根据式(14)更新一次得到的机组组合状态，可能不满足约束(6)，导致连续PSO算法优化出力失败。因此对于离散PSO算法的每次迭代，式(14)可计算多次，以保证每次迭代后确定的机组组合状态都满足约束(6)。同时为节省优化时间，设定最大计算次数，达到最大计算次数时仍不满足约束(6)，则按3.1.1节中确定的机组开机优先权依次安排已经满足最小停机时间约束且开机优先权较高的机组开机，直到满足约束(6)为止。式(14)的最大计算次数要根据实际来确定，设置的最大计算次数越大，则一次迭代约束(6)满足的机率越大，计算量也越大。

4基于降维求解的粒子群优化(DRPSO)算法流程

为兼顾算法全局搜索和局部寻优的能力，每次迭代粒子最大速度为机组出力范围的10%，且每个调度时刻的优化过程类似。

(1)分别初始化离散、连续粒子群算法的相关参数并读入机组参数、排污参数、负荷数据等。

(2)计算机组满负荷运行时的平均单位耗量，确定机组的开机优先权及基荷机组。

(3)对第t调度时刻机组启停状态进行初始化及迭代寻优，并进行最优负荷分配，具体流程见图1。

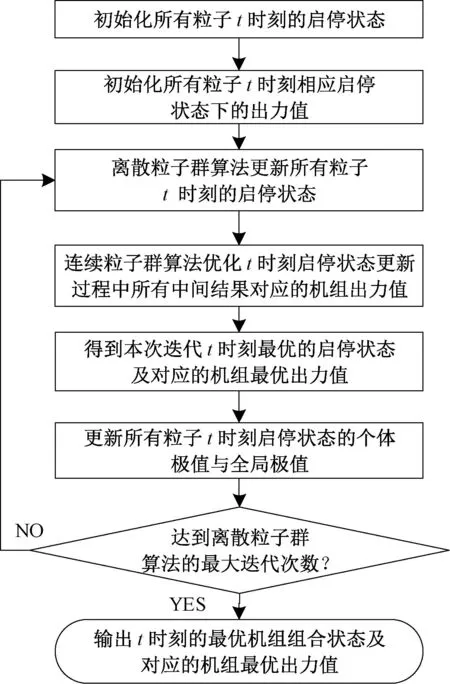
图1　第t时刻优化流程图Fig.1　Optimization flow chart of t moment

(4)判断是否全部调度时刻都优化完成。若是，则优化结束，否则进行下一个时刻的优化，t=t+1，转到第3步。

5结果分析

5.112机系统优化结果分析

本文首先对一个具有12台火电机组的中等电力系统做仿真分析，具体的发电机参数及负荷数据详见文献[5]。本文粒子群算法的主要参数为：学习因子c1=c2=2，惯性权重ωinitial=0.9，ωfinal=0.2，其中连续PSO算法最大迭代次数100，粒子数60，离散PSO算法最大迭代次数50，粒子数60，3.3节中持续代数上限为20，式(14)的最大计算次数为20。为与文献[5]的优化结果对比，本文所用数据及约束条件等均与文献[5]保持相同。

本文优化结果见表1，在全调度周期内，开机机组数目与负荷变化趋势大致相同，11、12号机组为基荷机组，一直开机，7、8号机组在整个调度周期内一直关机，原因是其经济性较差。通过分析表1与文献[5]中最优的机组组合方案可知，第1至第4调度时刻本文最优的开机数目与文献[5]相同，第5、第17、第18、第19调度时刻本文的最优开机数目比文献[5]多，其余调度时刻，本文中的最优开机数目都要少，且都保证满足爬坡约束，表明本文算法可明显减少开机机组数目。

本文与文献[5]中的混沌混合遗传算法(HCGA)、拉格朗日法(LR)、混合遗传算法(HGA)、混沌优化算法(COA)优化的火电机组能耗费用对比见表2。文献[5]中最优的HCGA方法虽在约束条件中列出了爬坡约束，但最后的优化结果并未体现出机组爬坡的限制。在本文考虑爬坡约束，而文献[5]中最优的HCGA算法不考虑的条件下，本文可减少能耗费用56 900元，而当本文也不考虑爬坡约束时，本文可减少能耗费用87 300元，表明了本文优化方法在经济性方面具有显著的优越性。

5.2不同规模系统优化结果分析

之后，本文采用机组数倍增的方法又对10机、40机、100机、200机、300机系统24时段进行了算例分析，以验证本文优化方法对机组数较多的大规模系统的适用性，并与文献[12]对比，所用数据及约束条件等均与文献[12]保持相同，DRPSO算法主要参数与上面12机系统相同，算法运行环境是：CPU为Core(TM)2 2.2GHz，Acer-PC，Matlab r2013a。优化结果对比见表3。

由于本文DRPSO算法采用的是降维的优化思想，对于每个调度时段的求解是根据前一个时段已确定的最优机组组合状态，因此当前时段的某些机组启停已在前一个时段由其最小启停时间约束确定，故只需优化剩余机组的启停状态。即通过降维优化，可减少寻找不可行解的时间，有效降低搜索量。文献[12]中的双重PSO算法是课题组之前的研究成果，通过与之对比，由表3可知，随着参与调度的机组数的增多，本文DRPSO算法在计算经济性和计算时间方面都有一定优势，对于求解机组数较多的大规模系统同样具有显著的优越性。

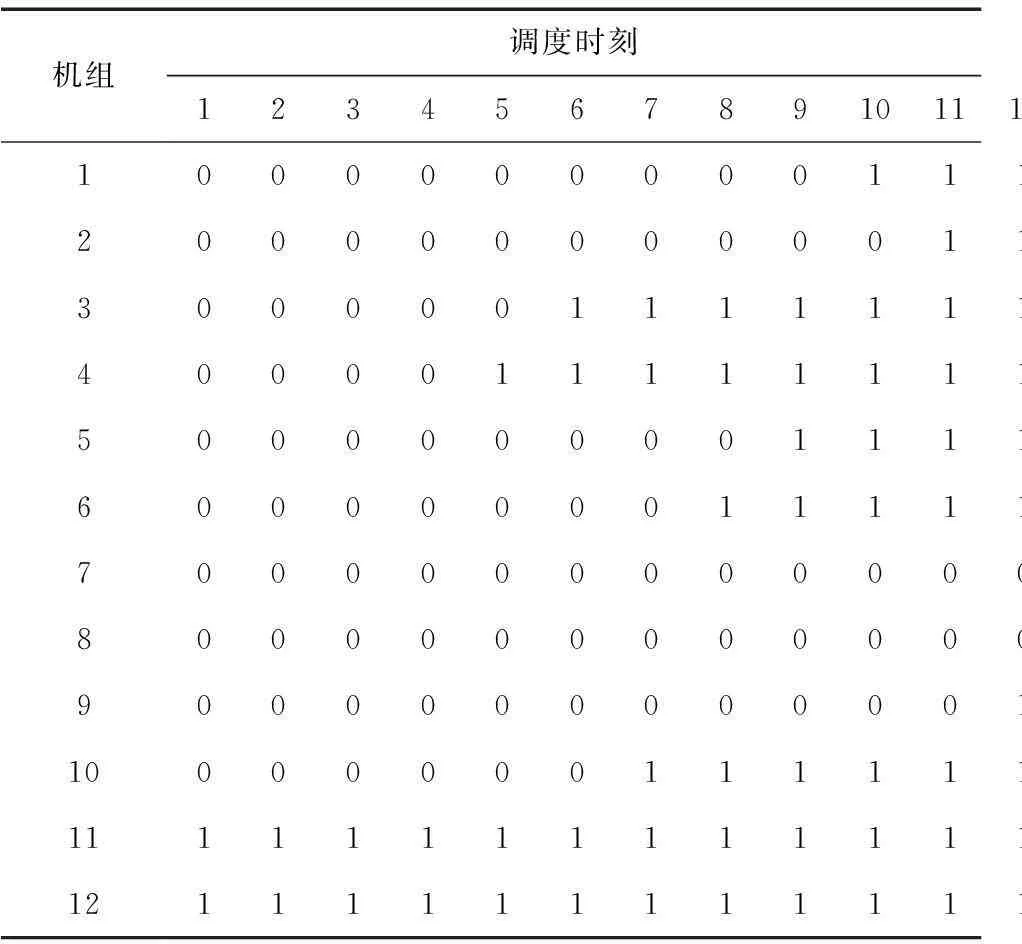
表1　12机系统最优机组组合状态

表2　12机系统优化结果对比

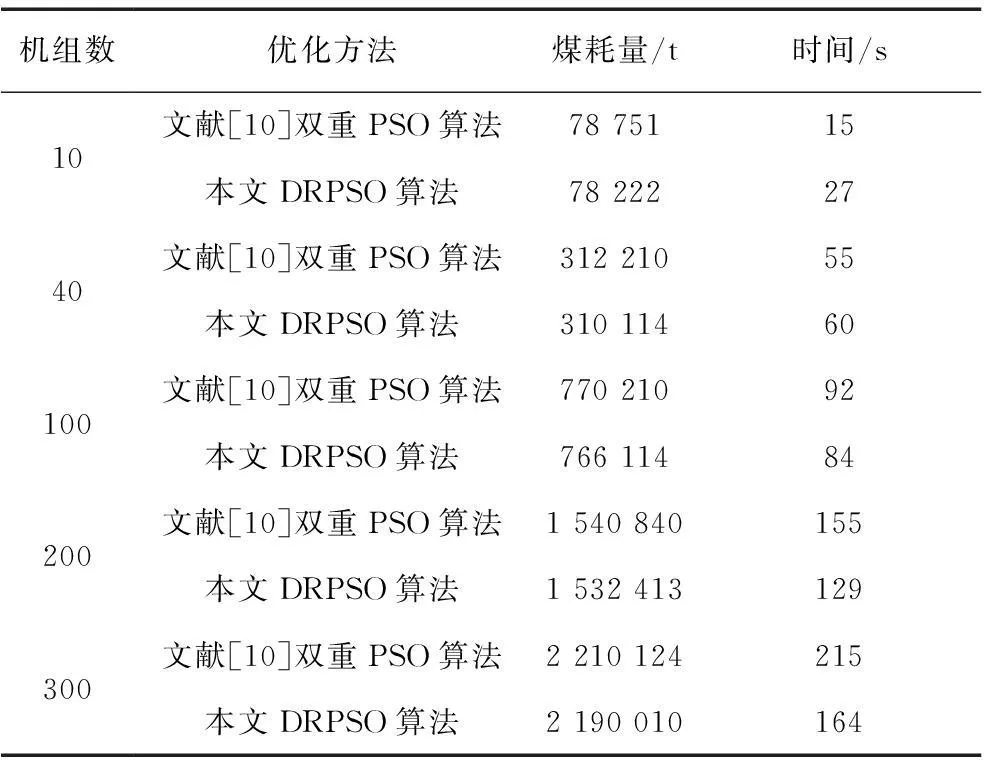
表3　不同规模系统机组煤耗量对比

6结论

本文在课题组之前对UC问题已有的研究成果基础上，提出采用降维的思想处理UC问题，将对整个调度周期的优化转化为对每个时刻依次、分别优化，并对初始解质量、约束处理、算法早熟等问题提出改进策略，使寻优都在可行域中进行。通过多个算例分析，结果表明本文优化方法在经济性方面具有很大优越性，且可明显减少开机机组数目，对于机组数较多的大规模系统更具优势。且本模型具有较好的通用性，在经适当的修改后，可应用到含大量分布式电源的微网调度模型中。模型存在的不足是，当将本方法应用到多目标优化中时，每个调度时刻都会产生多个非劣解，则整个调度周期内会产生大量非劣解组合，课题组下一步的研究重点将是如何解决在多目标优化中，非劣解组合过多的问题。

参考文献：

[1] Senjyu T, Shimabukuro K, Uezato K,et al. A fast technique for unit commitment problem by extended priority list[J]. Power Systems, IEEE Transaction on, 2003, 18(2): 882-888．

[2] 王治国, 刘吉臻, 谭文, 等. 基于快速性与经济性多目标优化的火电厂厂级负荷分配研究[J]. 中国电机工程学报, 2006, 26(19): 86-92.

[3] 张宁宇, 高 山, 赵 欣. 一种求解机组组合问题的快速拉格朗日松弛法[J]. 电力系统保护与控制, 2012, 40(19): 47-53.

[4] 李颖浩, 郭瑞鹏. 求解机组组合问题的多种群混沌蚁群算法[J]. 电力系统保护与控制, 2012, 40(9): 13-17.

[5] 王欣, 秦斌, 阳春华, 等. 基于混沌遗传混合优化算法的短期负荷环境和经济调度[J]. 中国电机工程学报, 2006, 26(11): 128-133.

[6] 王永强, 周建中, 覃晖,等. 基于改进二进制粒子群与动态微增率逐次逼近法混合优化算法的水电站机组组合优化[J]. 电力系统保护与控制, 2011, 39(10): 64-69.

[7] 袁晓辉, 苏安俊, 聂浩, 等. 面向启发式调整策略和粒子群优化的机组组合问题[J]. 电工技术学报, 2009, 24(12): 137-141.

[8] 江岳文, 陈冲, 温步瀛. 含风电场的电力系统机组组合问题随机模拟粒子群算法[J]. 电工技术学报, 2009, 24(6): 129-137.

[9] 吉 鹏, 周建中, 张睿,等．改进量子进化混合优化算法在溪洛渡电站机组组合中的应用研究[J]. 电力系统保护与控制, 2014, 42(4): 84-91.

[10] 陈烨，赵国波，刘俊勇，等．用于机组组合优化的蚁群粒子群混合算法[J]．电网技术，2008，32(6)：52-56．

[11] 袁铁江, 晁勤, 吐尔逊, 等. 大规模风电并网电力系统动态清洁经济优化调度的建模[J]. 中国电机工程学报, 2010, 30(31): 7-13.

[12] 李整, 谭文, 秦金磊. 一种用于机组组合问题的改进双重粒子群算法[J]. 中国电机工程学报, 2012, 32(25): 189-195.

[13] Senjyu T, Shimabukuro K, Uezato K, et al. A fast technique for unit commitment problem by extended priority list[J]. Power Systems, IEEE Transaction on, 2003, 18(2): 882-888.

Dual Particle Swarm Optimization Algorithm Based on Dimensionality Reduction for Unit Commitment Problem

ZHAI Junyi, REN Jianwen, LI Zheng, ZHOU Ming

(State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Baoding 071003, China)

Abstract:Dynamic economic dispatch of power system considering unit commitment is a high dimensional, complex and non-linear optimization problem. In this paper, a new method of dimension reduction was presented to optimize the large scale of unit on/off states and load dispatch problem, which converted from optimizing the entire dispatching cycle to doing each dispatching time respectively and orderly. That is, transform the optimization of matrix to row vector to reduce the solving dimension. Combined with the discrete and continuous particle swarm optimization (PSO) algorithm, the optimal unit combination states and the corresponding optimal units’ load dispatch of current dispatching time were obtained successively. Additionally, a new initialization strategy was proposed to improve the quality of the initial solution. Unit constraints, such as unit commitment constraint, lower and upper limits, were handling to make the optimization in the feasible region. The adoption of the priority list and intelligent adjustment strategy contributed to avoiding the premature of algorithm. Finally, the results indicate that this paper’s optimization methods have great economic superiority. Moreover, it can significantly decrease the number of generating units contrast with other literature and has more advantages in the large scale system.

Key words：unit commitment; dimensionality reduction optimization; dynamic economic dispatch; large scale system; dual particle swarm optimization

作者简介：翟俊义(1990-)，男，硕士研究生，主要研究方向为电力系统分析、运行与控制；任建文(1961-)，男，教授，主要研究方向为电网调度自动化；李整(1981-)，女，博士研究生，讲师，主要研究智能算法及其在电力系统中的应用；周明(1967-)，女，教授，博士生导师，主要研究电力系统运行、电力系统规划与可靠、电力市场等。

中图分类号：TM71

文献标识码：A

文章编号：1007-2691(2016)01-0032-07

基金项目：中央高校基本科研业务费专项资金资助项目(2015MS128); 国家自然科学基金资助项目(51177043); 河北省自然科学基金资助项目(F2014502081).

收稿日期：2015-04-10.

doi:10.3969/j.ISSN.1007-2691.2016.01.06