基于粒子群优化LS-WSVM的电机断条故障诊断

许允之，仝　年,2, 韩　丽, 胡　堃

(1.中国矿业大学 信息与电气工程学院，江苏 徐州 221116; 2.华北电力大学 电气与电子工程学院，河北 保定 071003)



基于粒子群优化LS-WSVM的电机断条故障诊断

许允之1，仝年1,2, 韩丽1, 胡堃1

(1.中国矿业大学 信息与电气工程学院，江苏 徐州 221116; 2.华北电力大学 电气与电子工程学院，河北 保定 071003)

摘要：为了准确检测出鼠笼式异步电机的转子断条故障，提出一种基于粒子群优化最小二乘小波支持向量机的诊断方法。首先，利用小波包或经验模态分解法提取出电机定子电流信号的特征向量，将特征向量分为训练集和测试集。再将训练集输入粒子群优化的最小二乘小波支持向量机进行训练，用训练好的最小二乘小波支持向量机对测试集进行分类。实验结果显示，此方法的故障诊断正确率明显高于最小二乘支持向量机的故障诊断方法。本文将小波分析和支持向量机结合使两者的优势互补，具有强大的泛化能力，为异步电机的转子断条故障诊断提出了一种新的方法。

关键词：故障诊断；粒子群优化；最小二乘支持向量机；感应电机；转子断条

0引言

转子断条是鼠笼式感应电机最主要的故障类别之一，大约占其总故障的10%[1-3]。电机断条故障较难发现，特别是1根断条的时候。若任由其发展，将会造成严重的后果。

检测电机断条故障的方法有很多。如分析定子电流信号来检测故障；利用振动信号中的故障特征频率来检测故障；根据电机转速的波动来检测故障；分析磁场的振动规律来检测故障；分析电机断电后定子残余电压来检测故障等。由于电机定子电流信号的采集电路简单，故障特征较明显，所以运用各种方法对定子电流进行分析来检测转子断条故障是当前研究的主要方向。当电机发生转子断条故障时，定子电流中将产生频率为fb=(1±2ks)f1(s为转差率，f1为电网频率)的故障特征分量[2-4]。多数分析方法都是基于此来提取转子断条的故障特征分量。

本文研究利用粒子群优化最小二乘小波支持向量机对电机转子断条故障进行诊断并判断断条根数。

1故障特征提取

电机故障特征的提取是电机故障诊断最重要的环节。由于故障特征频率与电网频率非常接近乃至被淹没，而且定子电流信号中夹杂许多噪声，所以故障特征很难提取出来。只对电流进行简单的傅里叶变换得到的频谱图往往不能显现明显的故障特征。小波分析法、经验模态分解法等时频分析方法已经广泛的应用于电机故障诊断中，取得了优于傅里叶频谱分析的效果。

1.1基于小波包的故障特征提取

故障特征频率分量的出现使正常电机和有断条故障电机的定子电流在小波包分解后各节点的能量产生差别，因此可以将各节点的能量作为特征向量。

根据Parseval定理可知，信号在时域中的能量等于其在频域中的能量，即信号经傅里叶变换或小波变换之后，其能量是守恒的。用公式表示为

(1)

式中：Ckj为小波分解系数，它具有能量的量纲；k为小波分解的层数，k=0，1，2，…；j为小波分解的节点号，j=0，1，2，…，2k-1，第k层第j个节点的信号能量为

(2)

为了方便运算，通常要将数据归一化处理。信号的总能量为

(3)

设对信号进行三层小波包分解，则特征向量为

(4)

1.2基于EMD的故障特征提取

经验模态分解(Empirical Mode Decomposition，EMD)法是一种自适应时频处理方法[7]。它能将复杂信号分解成若干个本征模函数(Intrinsic Mode Function，IMF)，各IMF分量包含了原信号在不同时间尺度的局部特征信号。EMD法不同于傅里叶变换和小波变换的是它是直观的、直接的、后验的和自适应的，非常适合分析非平稳信号。EMD法的本质是把非平稳信号进行平稳化处理，用若干个频率固定的IMF近似表示原来复杂的信号，把复杂问题简单化，便于分析。

正常电机和断条故障电机的定子电流EMD分解的前3个IMF分量所占的比例不同。因此，可以计算出前3个IMF的能量并将其归一化，作为特征向量。

第j个IMF分量的能量为

(5)

式中：l表示数据的长度，xj，i表示第j个IMF分量在i处的值。

利用下式求出前3个IMF的总能量：

(6)

将前3个IMF的能量归一化得到特征向量：

(7)

2最小二乘小波支持向量机

2.1最小二乘支持向量机

支持向量机(Support Vector Machine，SVM)以统计学习理论为基础，用结构风险最小化原则代替经验风险最小化原则，因而具有很好的泛化能力。

(8)

式中：ω为分类面的法线矢量；ξi为松弛变量；γ为正则化参数；b为偏移量。引入Lagrange乘子αi使优化问题变为

(9)

往往训练集不是线性可分的，需要利用非线性映射φ(·)将低维空间的训练集转化到高维空间，使其线性可分，用核函数实现在高维特征空间的内积运算。二次规划问题变为

(10)

式(10)中K(x)为核函数，常用的有线性核函数、多项式核函数、径向基核函数(RadialBasisFunction，RBF)和Sigmoid核函数[3]。

最小二乘支持向量机(LeastsquaresSupportVectorMachine，LS-SVM)是将标准支持向量机的不等式约束用等式约束代替，且将误差平方和损失函数作为训练集的经验损失，将优化问题简化成求方程组解的问题，大大提高了求解的速度。

最小二乘支持向量机的决策函数为

(11)

2.2小波核函数

根据Hilbert-Schmidt原理，只要是满足Mercer条件的函数，都可以作为支持向量机的核函数[6]。

本文选择常用的Morlet小波来构造小波核函数。

Morlet小波的表达式为

(12)

构造的Morlet小波核函数为

(13)

是一种支持向量机核函数。

Morlet小波支持向量机的决策函数为

(14)

2.3最小二乘小波支持向量机

最小二乘小波支持向量机(Least Squares Wavelet Support Vector Machines， LS-WSVM)与LS-SVM的基本原理相同，只是核函数用小波核函数代替。相对于LS-SVM，LS-WSVM将小波分析和支持向量机的优势互补，具有强大的泛化能力和抗噪能力。

3粒子群优化的LS-WSVM

3.1粒子群算法

粒子群优化算法(Particle Swarm Optimization，PSO)的提出是从“鸟群觅食”活动中得到启发。PSO算法把每个鸟的位置对应优化问题的一个解，把最优解比作食物，鸟群寻找食物的过程就是寻找最优解的过程。在PSO算法中，每只鸟或者说每个粒子，都有自己的速度和位置，速度对应其运动的距离和方向，位置对应一个解。

用vi(vi1，vi2，…，viD)表示第i个粒子的速度，用xi(xi1，xi2，…，xiD)表示第i个粒子的位置，D为解的维数。每个粒子目前发现的最好位置称为个体极值pi(pi1，pi2，…，piD)，所有粒子目前发现的最好位置称为全局极值pg(pg1，pg2，…，pgD)。粒子的速度和位置按照如下公式进行更新。

c2rand(1)(pg-xi)

(15)

(16)

式(15)中ω是惯性权重，ω的值越大，粒子群的全局搜索能力越强，局部开发能力越差；ω的值越小，粒子群的局部开发能力越强，全局搜索能力越差。c1、c2称为学习因子，控制了粒子向自身最优位置和全局最优位置运动的步长。rand(1)为[0，1]间的随机数。粒子的速度由三部分决定，第一部分vi代表粒子对上一次速度的继承；第二部分c1rand(1)(pi-xi)代表粒子的自身经验，即参考自身最优位置；第三部分c2rand(1)(pg-xi)代表社会经验，即参考全局最优位置。

如何选择ω的值对粒子群算法的优化能力有很大的影响。Shi和Eberhart提出了ω线性递减策略如式(17)所示。

(17)

式中：ωini为初始惯性权重；ωend为结束时的惯性权重。一般要求ωini≥ωend，使算法一开始时具有强大的全局搜索能力，避免陷入局部极值。然后加强局部开发能力，提高解的质量。

粒子群算法的步骤：首先，在允许范围内随机给出粒子群中每个粒子的初始速度和初始位置。然后，将粒子位置代入事先给出的适用度函数，求出粒子当前位置所对应的适用值，根据适用值更新个体极值和全局极值，就是用适用值更好的位置代替原来的pi和pg，若没有这样的位置，则pi和pg不变。再判断是否满足终止条件，满足，则结束；不满足，就按式(15)和式(16)更新粒子的速度和位置，如此循环。终止条件可以是满足迭代次数，也可以是pg对应的适用值达到要求。

3.2基于PSO优化LS-WSVM的电机转子断条故障诊断

支持向量机的正则化因子和核函数参数的取值对其性能有很大影响。PSO优化LS-WSVM是将支持向量机的正则化因子和小波核函数的参数作为粒子的位置，利用粒子群来寻找使支持向量机分类器性能达到最好时的正则化因子和核函数参数。如何判断支持向量机分类器性能的好坏将使用适用度函数，如式(18)所示。

(18)

式(18)中，li为对测试集进行测试时正确分类的个数；l为测试集总个数。因此，适用度函数的最大值为1，当其等于1时表示对应参数训练的支持向量机对测试集的所有样本都正确分类。当适用度函数的值等于1或粒子群满足最大迭代次数时停止算法。

PSO优化LS-WSVM电机故障诊断具体步骤如下：

(1)利用第2节介绍的小波包方法或经验模态分解方法提取三种类型电机定子电流的特征向量，并进行归一化处理；

(2)从特征向量中选取能区分故障类型的本质特征；

(3)将若干个本质特征向量分成训练集和测试集；

(4)将训练集输入粒子群优化的LS-WSVM进行训练；

(5)用训练好的支持向量机将测试集分类，观察其分类效果。

4诊断实例分析

实验所用的三相异步电动机型号为Y132M-4型，额定功率为7.5 kW,额定电压为380 V，电压额定频率为50 Hz，额定电流为15.4 A，额定转速为1 440 r/min(即额定转差率sN=0.04)，三角形接法,完好转子共有32根导条。有完好、断1条、断3条3种定做的转子。负载为8 kW的直流发电机，发电机给40个功率为200 W的灯泡供电，有空载、半载和满载3种运行状态。

由电机转子断条故障诊断实验获取满载状态下转子完好、转子断1条和转子断3条电机的定子电流信号，采样频率为5 000 Hz，每次采1 000个数据，共采样20×3组。其中一组的转子完好、转子断1条和转子断3条电机的定子电流波形如图1所示。

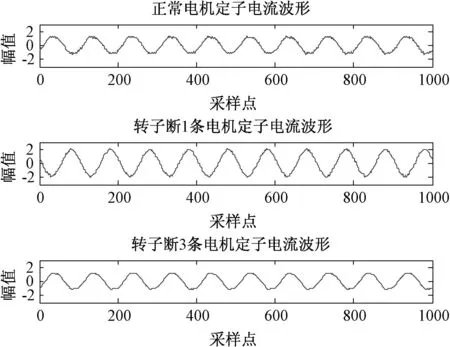
图1　正常电机与故障电机的定子电流波形Fig.1　Stator current waveforms of normal motor and fault motor

实验所用的MATLAB版本为R2014a，计算机操作系统为Windows 7旗舰版，处理器为英特尔第二代酷睿i5-2450M@2.50GHz 双核，内存4GB。

4.1基于小波包分解和PSO-WSVM的电机故障诊断实验研究

对20×3组连续的1 000个数据即10个周期的定子电流信号进行db6小波三层分解，计算8个节点的信号能量并进行归一化得到特征向量，选择第3、4频段作为本质故障特征向量。其中一组本质特征向量如表1所示,E2、E3分别为小波包分解第三层的第3、4个节点的能量，E为信号总能量。

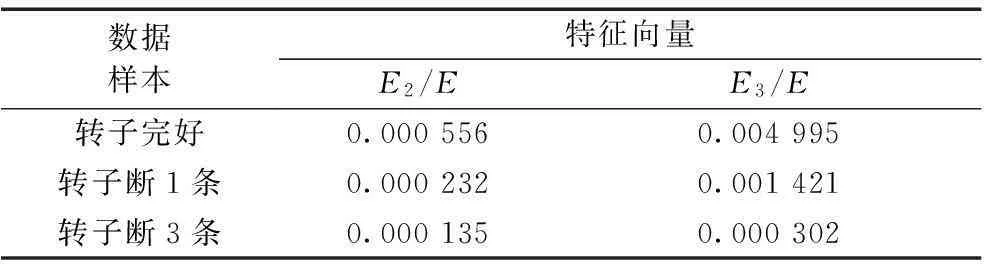
表1　小波包分解所得部分特征向量

将预处理好的20×3组数据中的15×3组数据作为训练集，剩下的5×3组数据作为测试集。采用“一对一”法构造多分类支持向量机。构造3个LS-WSVM二类分类器SVM1、SVM2、SVM3。设置粒子群有10个粒子，迭代次数为50，学习因子c1=2，c2=2 ，惯性权重ω按式(17)线性递减，其中初始惯性权重ωini=0.95，终止惯性权重ωend=0.4。得到最小二乘小波支持向量机的最优正则化因子γ=93.811 9，核参数σ2=24.247 2，按此设定LS-WSVM的参数进行训练。训练结果图如图2所示。

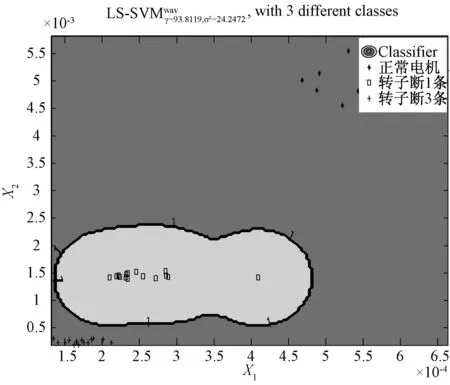
图2　LS-WSVM训练图Fig.2　Training map of LS-WSVM

由图2可知，训练准确率达到100%。用训练集和最优参数训练好的LS-WSVM对测试集进行分类，分类结果如表2所示。

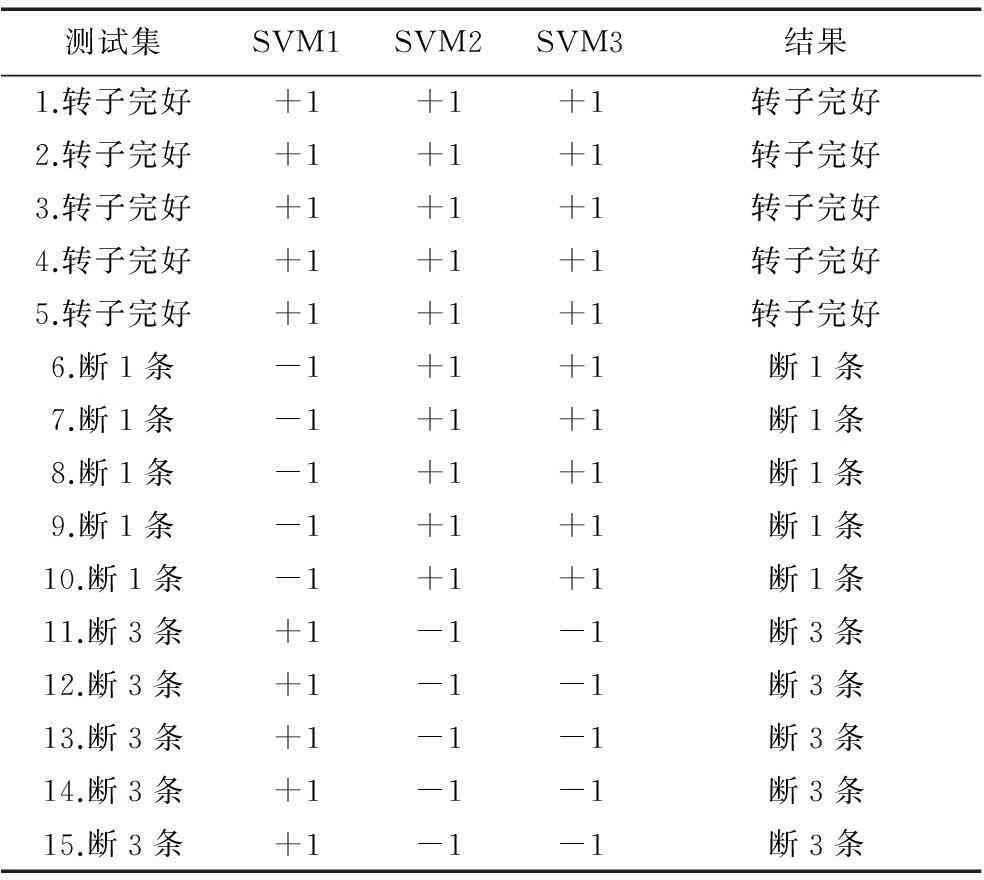
表2　测试集分类结果

测试集分类正确率为100%。表2中，各分类器的输出值与其所对应的决策结果如表3所示。

表3分类器输出值对应的决策结果

Tab.3Decision results corresponding to the output value of the classifier

分类器输出值+1-1SVM1转子完好转子断1条SVM2转子完好转子断3条SVM3转子断1条转子断3条

将PSO优化LS-WSVM与RBF核的LS-SVM进行对比，结果如表4所示。

表4　两种分类方法对比

从表4可以看出，两种方法的分类正确率均为100%。不论是小波核函数的支持向量机，还是运用小波包对输入支持向量机的数据进行预处理，都能得到很好的分类效果。说明小波分析法和支持向量机结合后优势互补。

4.2基于EMD和PSO-WSVM的电机故障诊断实验研究

对20×3组连续的1 000个数据即10个周期的定子电流信号进行经验模态分解，计算其前3个IMF的能量，归一化后得到特征向量。选择第2、3个IMF的能量作为本质故障特征向量。其中一组特征向量如表5所示，E2、E3分别为第2、3个IMF的能量，E为前三个IMF总能量。

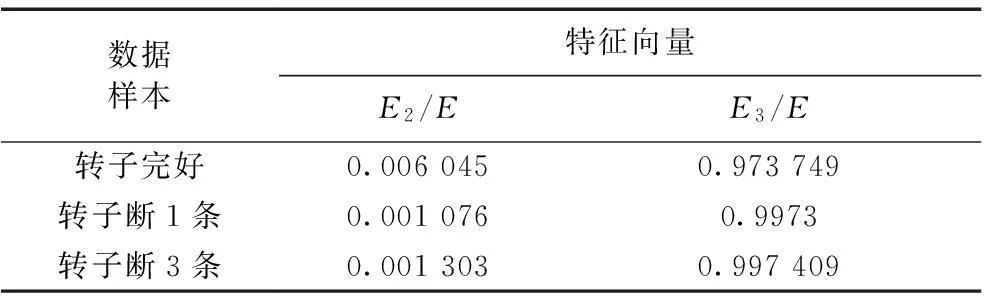
表5　EMD法所得部分特征向量

将预处理好的20×3组数据中的15×3组数据作为训练集，剩下的5×3组数据作为测试集。构造3个LS-WSVM二类分类器SVM1、SVM2、SVM3。对粒子群参数的设置同4.1节。得到LS-WSVM的最优正则化因子γ=814.742 2，核参数σ2=905.792 9，按此设定LS-WSVM的参数进行训练。训练结果图如图3所示。

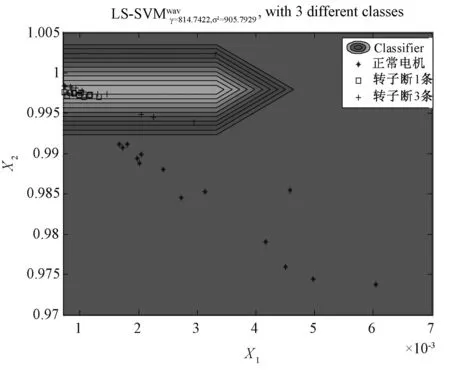
图3　LS-WSVM训练图Fig.3　Training map of LS-WSVM

训练准确率达到100%。用训练集和最优参数训练好的LS-WSVM对测试集进行分类，分类结果如表6所示。

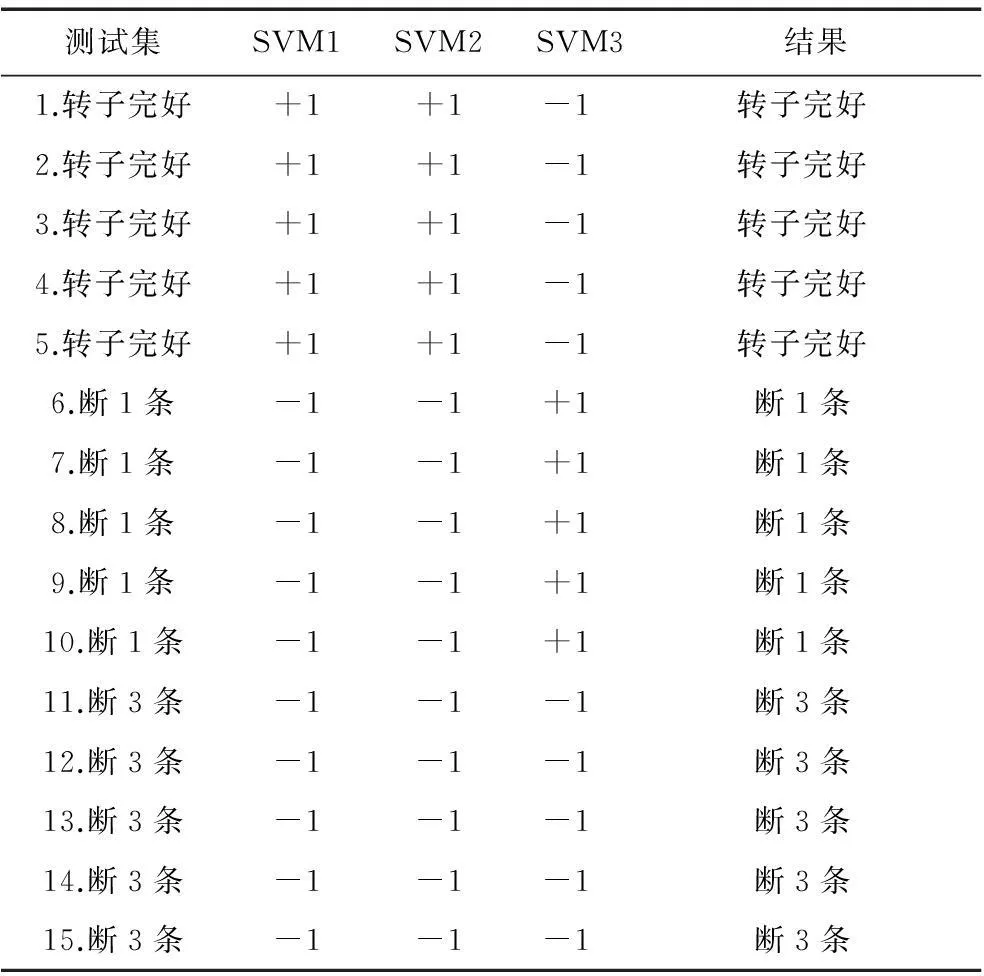
表6　测试集分类结果

测试集分类正确率为100%。

为了更好地体现出本文所提出的PSO优化LS-WSVM方法的优越性，将此方法和RBF核的LS-SVM进行比较，结果如表7所示。

表7　两种分类方法对比

从表7可以看出，对于EMD法提取的特征量，PSO-LS-WSVM的分类正确率远远高于LS-SVM。

5结论

本文提出了PSO优化LS-WSVM的模式识别方法。从表4和表7可以看出，不论是小波包提取的特征量还是EMD法提取的特征量，PSO-LS-WSVM都能将特征量组成的训练集和测试集进行正确分类，体现了小波分析和支持向量机结合后强大的非线性分类能力和泛化能力。为异步电机转子断条故障的定量分析提出了一种新的方法。

参考文献：

[1] 马宏忠.电机状态监测与故障诊断[M].北京:机械工业出版社,2008.

[2] 牛发亮.感应电机转子断条故障诊断方法研究[D].杭州：浙江大学，2006.

[3] 王攀攀.感应电机定转子故障的微粒群诊断方法研究[D].徐州：中国矿业大学，2013.

[4] 阳同光，蒋新华.感应电机故障诊断研究现状与发展趋势[J].微电机，2010,43(4)：68-72.

[5] 许允之，方磊，谭风雷,等.基于最小二乘支持向量机的故障电机诊断方法[J].实验技术与管理，2012，29(5)：35-37.

[6] 周建萍，郑应平，王志萍.基于Morlet小波核多类支持向量机的故障诊断[J].华东电力，2008,36(8)：76-80.

[7] 张兴，李孝全，谢一静.基于EMD分解的感应电机转子断条故障诊断[J].大电机技术，2011(5):21-23.

[8] 陈法法，汤宝平，董绍江.基于粒子群优化LS-WSVM的旋转机械故障诊断[J].仪器仪表学报，2012,32(12)：2747-2753.

[9] 崔万照，朱长纯，保文星,等.最小二乘小波支持向量机在非线性系统辨识中的应用[J].西安交通大学学报，2004,38(6)：562-565.

[10] 孙凯，王颖龙.支持向量机中Mercer核函数的构造研究[J].兵工自动化，2008,27(11)：40-42.

[11] 李军，赵峰.最小二乘小波支持向量机在非线性控制中的应用[J].电机与控制学报，2009,13(4)：620-625.

[12] 王昌吉，许允之.基于小波分析的异步电动机转子断条故障诊断研究[J].工矿自动化，2012,38(12)：54-57.

Broken Rotor Bar Fault Diagnosis of Motors Based on LS-WSVM Optimized by Particle Swarm Optimization Algorithm

XU Yunzhi1, TONG Nian1,2, HAN Li1,HU Kun1

(1.School of Information and Electrical Engineering, China University of Mining and Technology， Xuzhou 221116, China;2. School of Electrical and Electronic Engineering, North China Electric Power University， Baoding 071003, China)

Abstract:In order to accurately recognize the broken rotor bar fault of squirrel cage asynchronous motors, a method for diagnosis based on least square wavelet support vector machine (LS-WSVM) optimized by particle swarm optimization(PSO) algorithm is proposed. Firstly, wavelet package or empirical mode decomposition (EMD) was used to extract the feature vector of stator current signal of motors. Then the authors put the feature vector in LS-WSVM optimized by particle swarm optimization algorithm to train it. The trained LS-WSVM was used for fault classification. The experiment shows that the accuracy of this method is obviously higher than the fault diagnosis method of LS-SVM. It also shows that the combination of wavelet analysis and SVM has great generalization ability.

Key words：fault diagnosis; particle swarm optimization; least square wavelet support vector machine; induction motors; broken rotor bar

作者简介：许允之(1961-)，男，高级工程师，主要从事高电压技术与电机故障诊断的教学与研究工作。

中图分类号：TM307.1

文献标识码：A

文章编号：1007-2691(2016)01-0052-06

收稿日期：2015-05-25.

doi:10.3969/j.ISSN.1007-2691.2016.01.09