基于ITAE最优控制律的CFB锅炉优化控制

杨婷婷，洪　烽

(华北电力大学 工业过程测控新技术与系统北京市重点实验室，北京 102206)



基于ITAE最优控制律的CFB锅炉优化控制

杨婷婷，洪烽

(华北电力大学 工业过程测控新技术与系统北京市重点实验室，北京 102206)

摘要：在循环流化床(CFB)锅炉燃烧自动控制系统中，床温与主蒸汽压力耦合比较严重，常规控制算法的控制效果不是很理想。通过分析CFB锅炉的燃烧机理和动态特性，设计了部分前馈解耦控制器，实现了床温和主蒸汽压力的解耦。解耦后得到两个一阶惯性大迟延系统模型，针对CFB锅炉燃烧系统纯迟延较大对控制带来的挑战，应用ITAE最优控制率，对工业现场最常见的PI控制回路进行二次优化控制，并给出了控制器参数的求取方法。仿真结果说明该方法优化的结果各个性能指标较好。此优化方法算法简便，控制效果理想，且适合工程应用。

关键词：CFB锅炉；ITAE最优控制律；优化控制

0引言

循环流化床(CFB)锅炉燃烧技术作为一种高效的洁净煤燃烧技术，已经成为传统燃煤锅炉的有效补偿，发展前景广阔。在CFB锅炉中，燃烧系统的自动控制投入率低一直影响着实际运行效率，一方面对CFB锅炉内部机理的了解还不够全面深入，另一方面自动控制系统还有较大改进优化余地。随着机组的大型化成为趋势，这一问题亟需解决。

床温是燃烧系统的核心控制性能指标之一，其与很多变量相互耦合，尤其与主汽压力的耦合效应最为严重[1]。通过分析循环流化床锅炉的燃烧机理和动态特性，设计了部分前馈解耦控制器，实现了床温和主蒸汽压力的解耦。将2×2耦合对象控制问题转化为V-P回路和M-T回路的控制问题。解耦得到的两个控制回路均为一阶惯性加大迟延模型。针对在控制上具有挑战性的纯迟延环节，在工业现场最常用的PI控制器基础上，利用ITAE最优控制率设计改进控制器，并给出确定参数的方法，使各性能指标能达到综合最优。

1CFB锅炉燃烧控制系统模型

1.1CFB锅炉燃烧系统控制目标和难点

CFB锅炉燃烧控制系统的基本任务是协调燃料量、送风量之间的关系，以满足机组负荷的要求，保证锅炉燃烧的经济性和机组运行的安全性与稳定性。

CFB锅炉燃烧系统具有多参数、强耦合、大滞后和非线性等特点，部分控制对象还具有逆向响应的特性。此外物料的再循环和收集分离，床层温度的范围要求等也需要考虑。这些特点和特性给其自动控制系统的设计带来了很大的难度，也使锅炉燃烧过程控制变得异常困难[2]。图1所示为CFB锅炉多变量之间的关系。

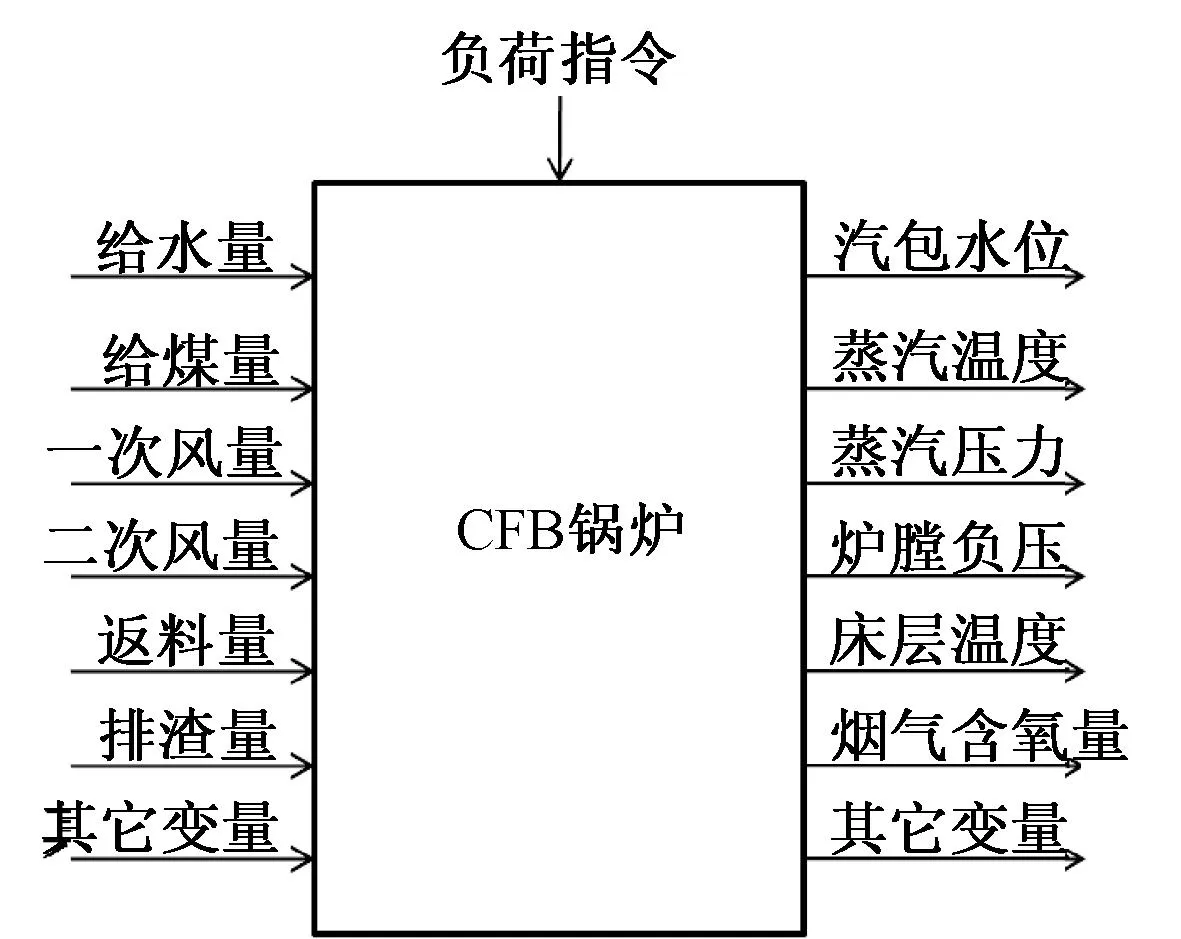
图1　循环流化床锅炉变量关系Fig.1　The variable relationship between the CFB boiler

这些变量和回路之间的耦合关系和复杂的燃烧特性导致建立系统的精确数学模型异常困难[3]。而建立起来的数学模型往往有一定的局限性，这使得传统控制理论和方法难以应用。

此外，CFB锅炉燃烧过程中的延迟比普通煤粉炉大很多，燃料量-蒸汽负荷通道具有大延迟的特点，采用给煤量来调节床温存在很大的滞后性[4-7]。在CFB锅炉燃烧控制系统的设计中，克服延迟是必须考虑的。

床温是循环流化床锅炉运行的重要参数，它不仅关系到锅炉能否安全稳定运行，合适的床层温度还能有效提高脱硫效率、更好地抑制氮氧化物的生成。影响床温的变量有很多，起主要作用的是一次风量和给煤量。床温对一次风量的变化响应迅速，几乎没有延迟，由于一次风量维系炉内的循环流化、旋风分离器的循环流化，其调节范围比较小。给煤量的变化同时影响床温和主蒸汽压力。但是给煤量对床温的调节存在较大滞后和延迟，往往需要几分钟[6,7]。

主蒸汽压力是CFB锅炉燃烧过程需要控制的另一个重要参数，它表征着锅炉产生的热量对负荷指令的跟踪情况。一次风量调整幅度与其对炉内物料流化的影响成正比，因此会引起主汽压力的波动[8]。改变给煤量，由于炉体内工质温差的存在造成了炉内传热状况发生改变，主汽压力也随之改变，而此过程响应较慢，同样存在较大的滞后。

1.2CFB锅炉燃烧系统的模型

数学建模方法常用的是机理建模和试验建模以及两者相结合。目前，对CFB锅炉燃烧过程的建模成果总体分为两类[9]：一类是根据炉内气固流态化特性和燃烧传热过程特性结合物质能量平衡建立的机理模型；另一类是从工程角度考虑，在现场通过阶跃扰动试验建立了某些模块的传递函数模型，或通过系统实际运行数据，建立了输入输出变量之间的智能模型。

CFB锅炉燃烧过程中，床温和主蒸汽压力同时受给煤量和一次风量的影响，当它们中的任意一个偏离设定值，通过给煤量或一次风量调节时，都会使另一个变量发生改变。因此，床温和主蒸汽压力的强耦合是循环流化床锅炉燃烧控制的主要难点。选取它们之间的传递函数阵如式(1)所示：

(1)

式中：P，T分别表示主蒸汽压力和床温；V，M分别表示一次风量和给煤量。

除了强耦合，循环流化床的燃烧系统还有大延迟，具体传递函数如下所示：

(2)

上式中的各变量在一定范围内变化，其中Kθ1在5～10之间，Tθ1在100～200 s，τθ1在30～60 s，Kθ2在3～5之间，Tθ2在80～180 s，τθ2在30～50 s，Kp1在4～6，Tp1在150～300 s，τp1在 60～100 s，Kp2在5～8，Tp2在80～150 s，τp220～40 s。

表1列出了CFB锅炉燃烧系统3种工况下个参数的取值[10]。

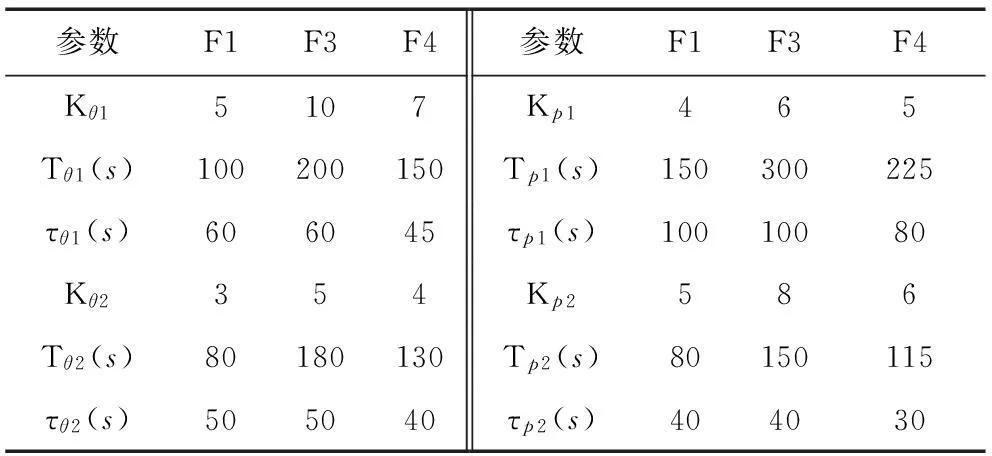
表1　CFB锅炉燃烧系统的3种工况

1.3相对增益的计算

对于多变量系统，由于各控制回路之间的耦合，一般控制方法无法推广使用。为了简化上述双输入双输出控制系统的设计和分析，需要对其进行解耦：首先计算各个回路的相对增益来分析各个输入量对输出量的影响程度，确定输入变量和输出变量之间的最佳匹配。然后进行解耦。

对于一个双入双出的系统来说，其输出变量yi对输入变量ui的相对增益定义为

(3)

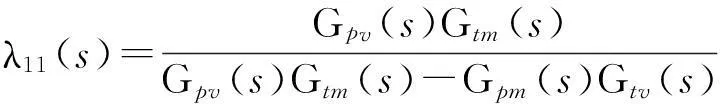
系统的相对增益矩阵为

现在改变输入和输出变量的匹配方式，即传递函数阵变为

(4)

则相对增益变为

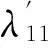
表2CFB锅炉3种工况下相对增益

Tab.2The relative gains of CFB boiler under three different conditions

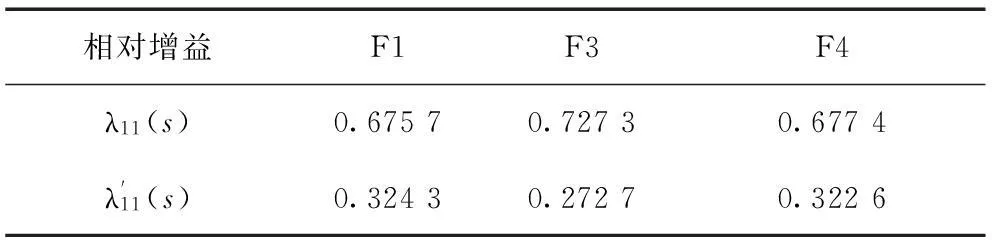
相对增益F1F3F4λ11(s)0.67570.72730.6774λ'11(s)0.32430.27270.3226

在控制理论中，通常情况下，当λ11<0.7或λ11>1.3时，表明系统中存在严重耦合，故选取的CFB燃烧系统的两个回路之间存在严重耦合，需要对其进行解耦设计。由表1可知3种工况下，相对增益λ11较接近与1，故选用输出变量主汽压P与输入变量一次风量V为一个回路。

1.4部分前馈补偿解耦

目前，对循环流化床锅炉燃烧系统解耦控制的方法很多，理论基础研究比较完善，且产生了一定的工业应用价值，如传统的PID解耦控制以及神经网络解耦、模糊解耦、自抗扰解耦、自适应解耦等多种先进解耦控制策略[10-13]。

前馈是按照干扰作用的大小来进行控制的，当扰动一出现，就能根据扰动的测量或者计算得到前馈控制量，提前产生调节作用以消除扰动造成的偏差或波动。基于此原理，采用部分前馈补偿解耦方法来消除两个回路之间的耦合。这种方法结构简单、易于实现，在双输入双输出系统中广泛应用。其原理图如图2所示[14-16]。

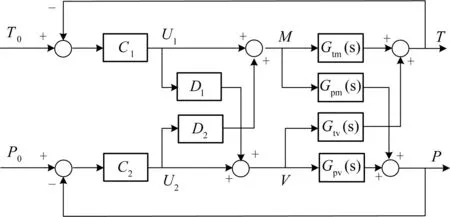
图2　前馈补偿解耦结构图Fig.2　The feed-forward decoupling structure diagram

图2中，P0，T0分别是主蒸汽压力和床温的设定值；C1，C2是解耦后两个独立控制回路的控制器；D1和D2分别是两个回路的解耦补偿器。从图中可以看出，当想要调节床温T而改变设定值T0时，将通过传递函数Gpm(s)影响主蒸汽压力P。同理，主蒸汽压力设定值P0改变时，会通过函数Gtv(s)影响床温T的稳定。为了消除这种耦合，使主蒸汽压力P完全不受给煤量M影响，且床温T完全不受一次风量V影响，应满足下列条件：

(5)

因此，可以得到解耦补偿器的表达式：

(6)

然而，考虑到超前环节无法实现，部分解耦控制器通常采用如下形式：

(7)

可以看出，前馈补偿解耦方法计算量少，结构简单，但有的被控系统中，耦合函数的延迟时间小于被控对象的延迟时间，造成前馈解耦补偿器含有超前环节，而超前环节很难实现。此时有

(8)

由表1可知τp2为30或者40，τp1为80或者100，所以e-τp2s-e-τp1s的数量级在10-18，同理e-τθ1s-e-τθ2s也很小，故采用部分解耦后可得

(9)

可知虽然采用部分解耦，其效果基本等同于完全解耦。

通过部分前馈补偿解耦，燃烧系统被解耦成两个相对独立的回路：V-P控制回路和M-T控制回路。解耦后的两个相对独立的回路被控对象均视为如下的形式：

(10)

该一阶惯性加纯迟延模型也是工业过程中常见的对象模型。大迟延是公认的控制难题，通常大滞后问题几乎都采用纯迟延一阶惯性环节作为控制对象。在CFB锅炉燃烧系统的上述3种典型工况下，解耦后的控制对象等效模型的特征参数K，Td，T。如表3所示。

表3被控对象等效模型的特征参数

Tab.3The characteristic parameters of the equivalent model of the controlled object

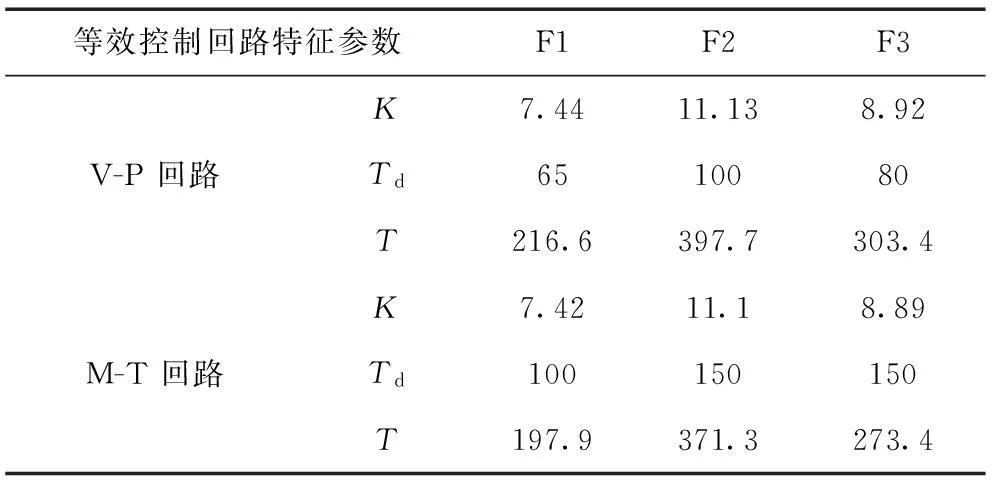
等效控制回路特征参数F1F2F3K7.4411.138.92V-P回路Td6510080T216.6397.7303.4K7.4211.18.89M-T回路Td100150150T197.9371.3273.4

2基于ITAE最优控制律优化控制

2.1ITAE理论推导

纯时滞系统是一个难控系统，这是因为这类受控系统的数学模型中，有一个无穷维因子e-Tds，根据最优控制论，要把这类受控系统控制到最优运行状态，必须先解决两个前提条件：一、有一个无穷维观测器；二、有一个无穷维控制器。用物理办法无法实现两个前提条件，因此，此类系统的优化控制长期无法实现。

半个世纪以来，为了应付工业过程的控制要求，经历了PID控制、智能PID控制和常规的以PID为控制器的一些优化控制[8,13,16]。实质上都不是真正的最优控制，因为PID控制器只有两维三参数，根本无法实现无穷维受控对象的最优优化。

1958年．Smith用补偿的方法，消除纯时滞因子后，再用常规办法设计控制器参数[17]。全补偿时，效果很好。因为在这个条件下，系统变成线性定常系统，可以在有穷维相空间内，实现它的优化控制，但是一旦出现欠或过补偿，受控系统又回到无穷维相空间了，性能指标急剧恶化，为了解决这个缺点，后来出现了种种改进型Smith预估器，也都没有实现最优优化。CFB锅炉动态特性复杂，很难建立其精确的数学模型，并且过程的参数时变，Smith预估器不再适用。

为了从根本上解决纯时滞系统优化控制问题，文献[18]提出了一种新的控制原理，纯时滞系统二次优化控制原理，先用有限维近似数学模型逼近无穷维因子，在有穷维空间内，实现ITAE优化控制，然后回到无穷维空间再优化。

应用此法设计改进PI控制器，并计算最优参数。对于获得的传递函数，不失一般性采用一阶分时模型

(11)

式(11)是一个二阶定常受控对象。根据文献[18]的可综合准则，为了把它综合成位移无静差ITAE最优控制系统，开环传递函数中至少得有一个积分环节，系统的结构图如图3所示，Kc为待定参数。

图3　一阶分时模型Fig.3　First-order time-sharing model

相应的开、闭环传递函数分别为

(12)

(13)

式(13)有三维，但可控参数只有一个Kc，根据ITAE最优可综合准则，至少需要增加两个独立可控量。为了提高系统的抗干扰能力，可采用状态反馈来实现第一次优化，见图4所示结构。

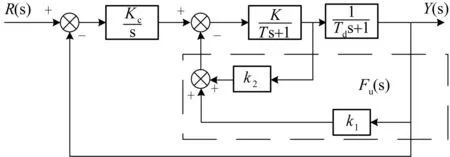
图4　系统第一次优化结构图Fig.4　The first Optimization of system structure

图4系统开环传递函数为

(14)

而三阶位移无静差ITAE最优开环传递函数为

(15)

令式(14)和式(15)两式s同次幂项系数相等，整理后，便得到第一次优化控制器3个参数解方程

(16)

其中ω3=KcKd/TT，β1，β2为ITAE最优传递函数参数集，这里不失一般性，取β1为2.25，β2为1.98，可以看出只要确定ω，就能确定3个参数。

回归到无穷维因子，此时状态反馈阵传递函数为

相应的结构图如图5所示。

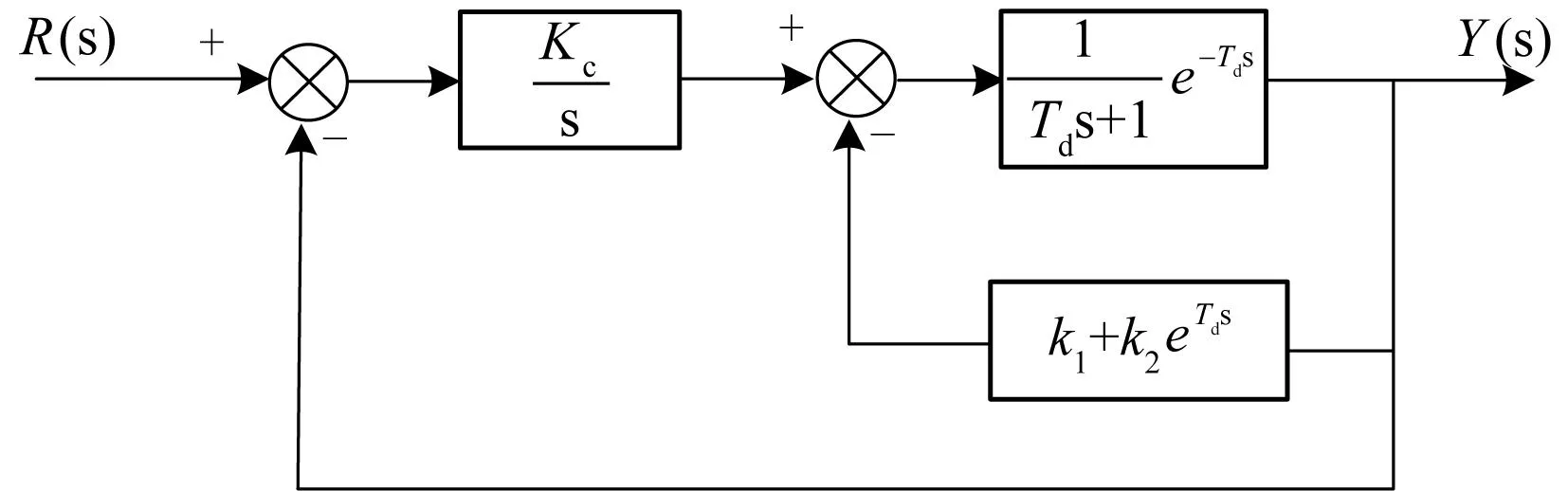
图5　系统第二次优化结构图Fig.5　The second optimization of system structure

对于此系统进行寻优，给定一系列ω数值，目标函数为

式中：σ%为系统超调量；ts为系统的调节时间。

2.2优化控制仿真

不失一般性，对F1工况下的V-P回路进行基于ITAE最优控制律的优化控制，传递函数为

只需在现场的PI控制回路中增加两个比例环节，例如图4。利用ITAE最优控制律的两次寻优，易得出参数Kc=0.001 89，k1=0.297，k2=-0.005 42，回路对象的阶跃响应如图6，其中另外两条曲线为PI自整定的结果。从中可知，经过基于ITAE最优控制律优化控制后的对象超调为0，过渡平缓，调节时间较小。总体来说，性能指标比原先回路PI自整定的结果理想。

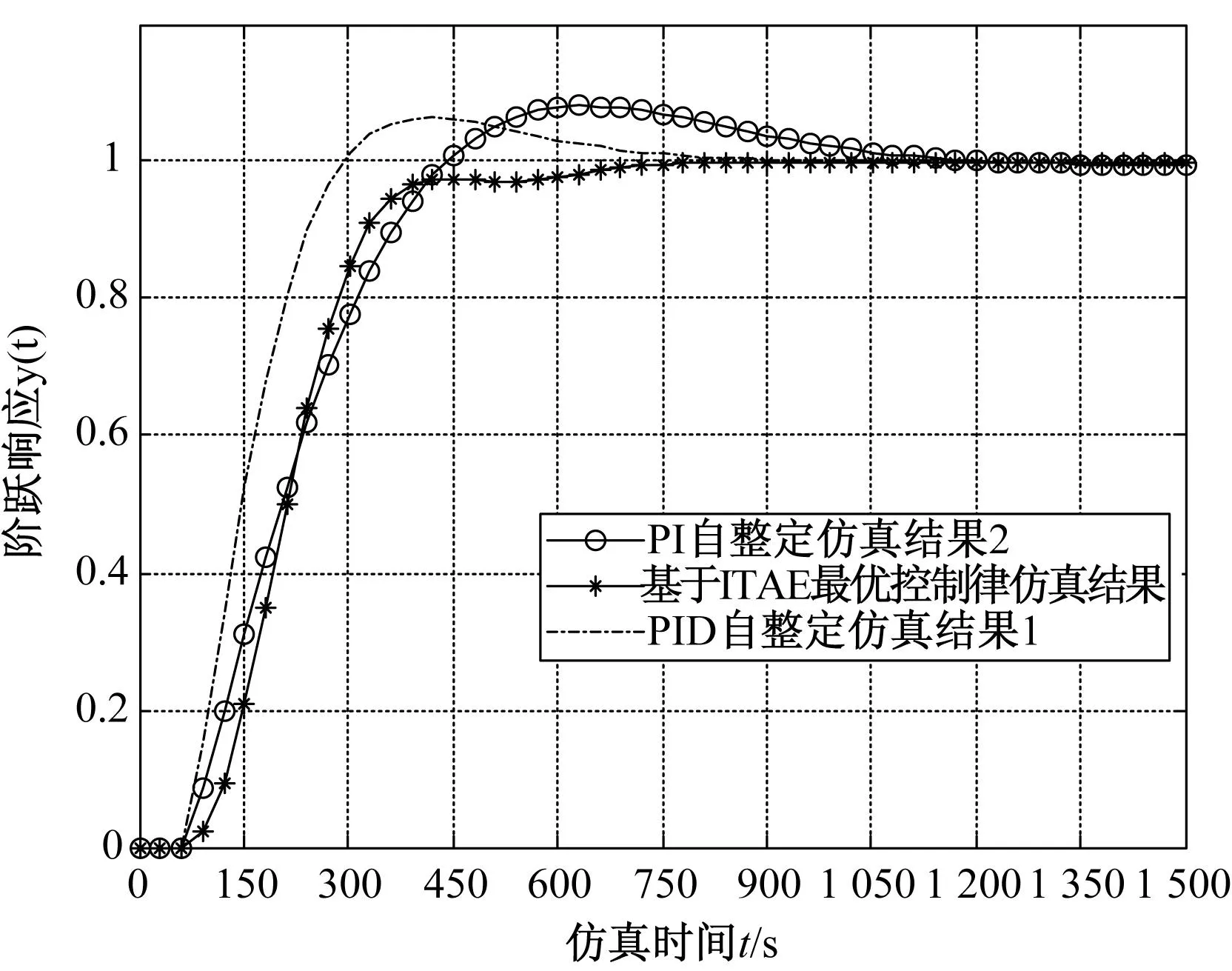
图6　仿真结果图Fig.6　The simulation results

3结论

实现CFB锅炉燃烧系统的自动控制难度很大，主蒸汽压力和床温CFB锅炉中至关重要的两个参数，它们表征着锅炉运行状况是否安全稳定，也是最难控制的两个参数，这两者之间存在强耦合。应用部分前馈解耦方法，对两者进行解耦，得到了两个互不影响的独立控制回路。该解耦方法具有普遍适用性。

针对解耦后的一阶惯性大迟延系统纯迟延环节控制的困难，应用ITAE最优控制率，对最常用的PI控制回路进行二次优化控制，设计的控制器结构形式简单，参数求解方便。仿真结果说明该方法优化的结果各个性能指标较好，有一定的优越性。

参考文献：

[1] 朱国桢，徐洋．循环流化床锅炉设计与计算[M].北京：清华大学出版社，2004．

[2] 岑可法，倪明江，骆仲泱，等.循环流化床锅炉理论设计与运行[M].北京：中国电力出版社，1998.

[3] 杨晨, 何祖威. 大型循环流化床锅炉整体动静态数学模型的建模方法研究[J]. 动力工程, 2002, 22(4): 1841-1846.

[4] 蒋敏华，肖平.大型循环流化床锅炉技术[M].北京：中国电力出版社，2009.

[5] 李政，张巍．循环流化床锅炉动态仿真试验平台研制[J]．清华大学学报(自然科学版)，1999，39(3)：100-102．

[6] 高明明, 刘吉臻, 牛玉广，等. 基于EKF技术的CFB锅炉残碳量估计[J]. 热能动力工程, 2013, 28(5):492-496.

[7] 高明明, 岳光溪, 雷秀坚，等. 600 MW超临界循环流化床锅炉控制系统研究[J]. 中国电机工程学报, 2014, 34(35): 6319-6328.

[8] 钟亮民, 刘吉臻, 张恒，等. 基于多变量内模解耦的 CFB 锅炉燃烧控制研究[J]. 动力工程学报 ISTIC, 2014, 34(4)：298-306.

[9] 孙剑. 大型循环流化床锅炉燃烧系统特性与建模研究[D].北京：华北电力大学, 2010.

[10] 席学军. 循环流化床锅炉燃烧系统的自抗扰控制研究 [D].北京： 清华大学, 2004.

[11] 付萍, 姚丽欣, 李小珂，等. 循环流化床锅炉床温系统控制特性分析及参数优化[J]. 华北电力大学学报, 2005, 32(5):89-91.

[12] 李永华, 黄治坤, 李响，等. 330MW循环流化床锅炉优化调整试验研究[J]. 华北电力大学学报, 2012,39(2):103-107.

[13] Kaya I. IMC based automatic tuning method for PID controllers in a Smith predictor configuration [J]. Computers & chemical engineering, 2004, 28(3): 281-290.

[14] 张秀喜, 夏洪. TITO系统前馈解耦补偿器含有超前环节的近似处理方法 [J]. 电子质量, 2012,(6): 5-7.

[15] 程启明, 李婧, 程尹曼,等. 循环流化床锅炉燃烧过程的多变量解耦控制系统研究 [J]. 华东电力, 2009,(5): 819-823.

[16] Ji-zhen L, Zhen-fang Z. Partial feed-forward decoupling based PI control of CFBB combustion system[C]//Control and Decision Conference (2014 CCDC), The 26th Chinese.IEEE, 2014: 1473-1477.

[17] Smith O J M. A controller to overcome dead time[J]. ISA Journal, 1959, 6(2): 28-33.

[18] 项国波. 时滞系统优化控制[M]. 北京：中国电力出版社, 2009.

Optimization Control of CFB Boiler Based on ITAE Optimal Control Law

YANG Tingting, HONG Feng

(State Key Laboratory of Measurement and Control New Technology and System for Industrial Process, North China Electric Power University, Beijing 102206, China)

Abstract:In the circulating fluidized bed (CFB) boiler combustion automatic control system, the bed temperature couples seriously with main steam pressure. Therefore, the conventional control algorithm can not achieve its ideal effect. Based on the analysis of the combustion mechanism and dynamic characteristics of CBF boilers, partial feed-forward decoupling is proposed and it can successfully convert the transfer function of the main steam pressure and bed temperature to two independent loops. The decoupled loops are in the form of one step with big delay. To meet the challenge of CFB boiler combustion system by big delay, the ITAE optimal control rate is applied to the most common PI control circuit, combining the rapidity and accuracy of control systems. Based on this criteria, the design and parameters tuning method of PI controller are provided, which can realize the effective control of this kind of controlled objects. The simulation results indicate that the system, to which this method has been applied, has a better control performance. Overall, it is found that this simple optimal control can achieve its ideal control effect, which is suitable for the engineering application.

Key words：circulating fluidized bed boiler; ITAE optimal control rate; optimization control

作者简介：杨婷婷(1981-)，女，博士，讲师，主要研究方向为大型燃煤机组节能优化控制；洪烽 (1991-)，男，硕士研究生，主要研究方向为大型循环流化床机组状态监测与优化控制。

中图分类号：TK323

文献标识码：A

文章编号：1007-2691(2016)01-0065-06

基金项目：国家重点基础研究发展计划项目(973计划) (2012CBC215203).

收稿日期：2015-05-14.

doi:10.3969/j.ISSN.1007-2691.2016.01.11